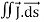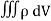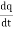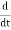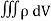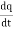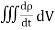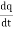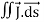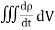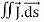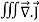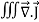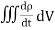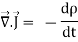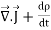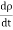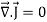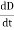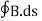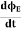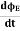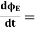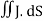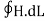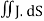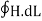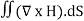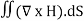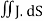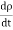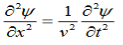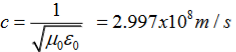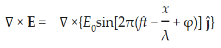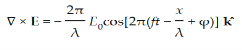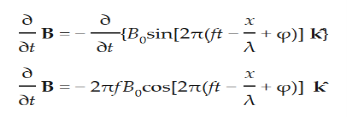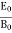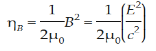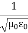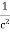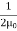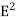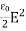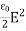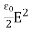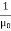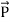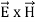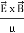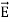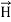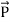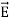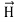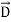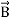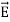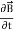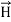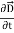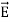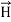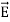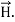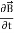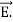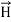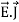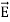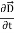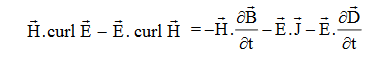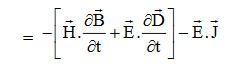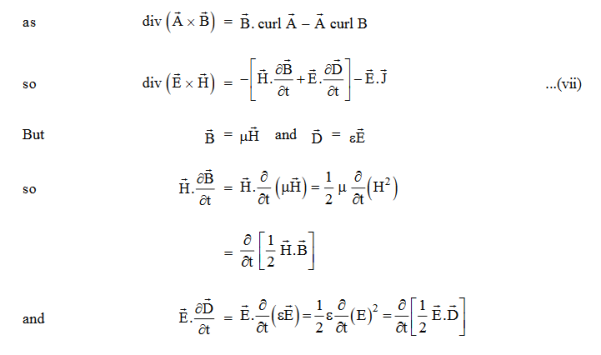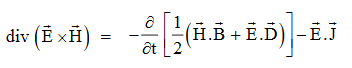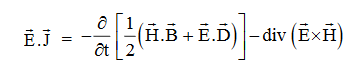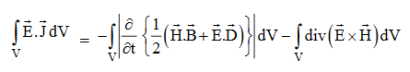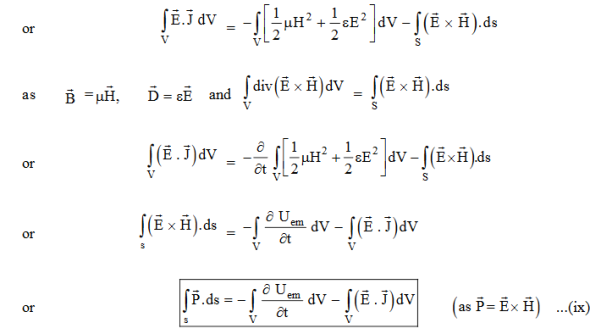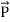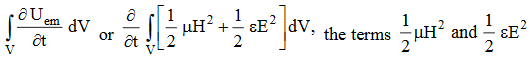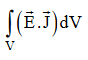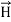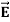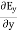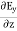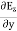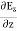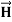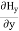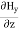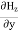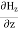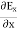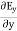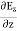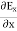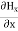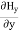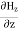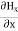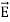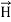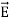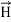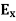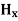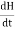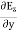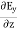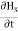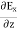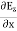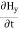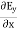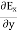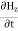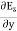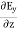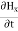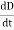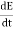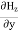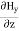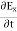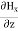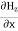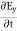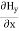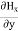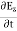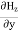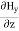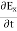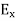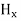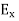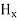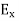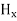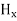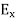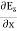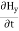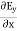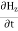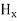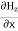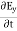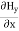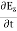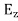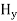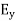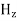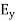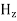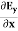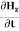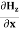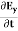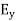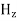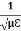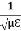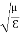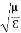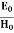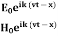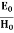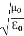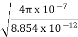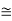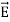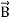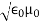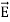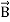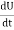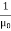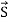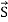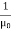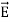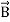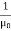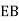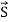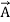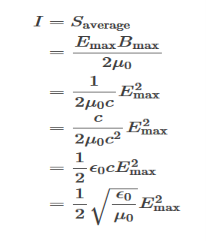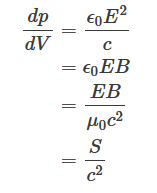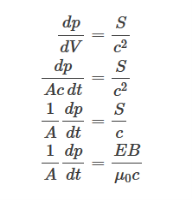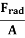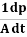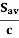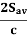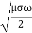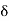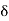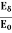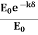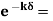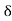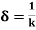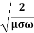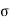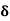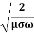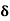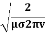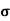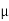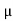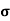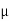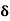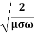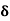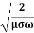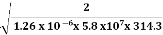Unit - 2
ELECTROMAGNETIC FIELD THEORY
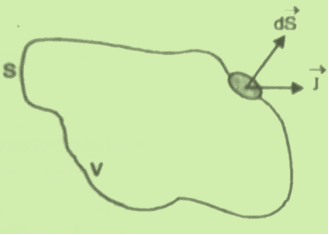
Consider a closed surface S enclosing a Volume V through which currents are flowing. Let I be the current passing through the surface at any time t. Consider a small area
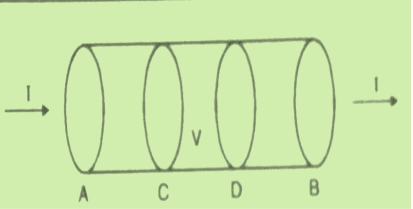
dI = the total current flowing out through the closed surface S at time t is I = Suppose is ρ the Volume Charge density of charges inside the surface S. Then the total charge inside the Volume V is q = Since the current is flowing outward is it mean that charge within the enclosed surface is decreasing with time. The time rate of decrease of charge is
The negative sign shows that the charge inside the surface S is decreasing with time. The above equation can be written as
Since the charge is conserved, the current flowing outward through the closed surface must be equal to the rate of decrease of charge. Thus I = Using equation (2) and (5), it becomes
According to divergence theorem
Using this result in equation (6) we obtain
This equation holds good for arbitrary volumes. Therefore, the integrands must be equal. Hence
This equation is called equation of continuity. It is the mathematical statement of law of conservation of charge. SPECIAL CASE Consider a conductor AB through which a steady current I is flowing. The current I is said to be steady if charge is flowing per unit time through any two any sections C and D is the same. This means that the total amount of charge entering the volume V through C is equal to the charge leaving the volume V through D. Thus there is no change in the volume charge density in the volume V with time i.e.
We may define steady current as that current in which the charge density is independent of time. Using equation (7) we obtain
This is known as the equation of continuity for steady currents. |
Displacement current is the rate of change of electric displacement field. The type of current which passes through a conductor is known as conduction current and is caused by the actual movement of electrons through the conductor. This type of current is mostly used in our day to day life. There is also another kind of current, which is known as displacement current. Displacement current differs from the conduction current because the displacement current does not involve electrons' movement. The displacement current has enormous importance for the propagation of electromagnetic waves. In electromagnetism, displacement current is a quantity appearing in Maxwell's equations that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. It is mathematically represented as ID = JD S = S Where S = Area of the plate of the capacitor ID = Displacement current JD = Displacement current density D = εE where ε is permittivity of the medium During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor. According to Ampere's law, the magnetic field should not present between the plates as there is no current, but in reality, the magnetic field exists there. Maxwell formulated this limitation of Ampere's law by adding a term in the equation of Ampere's law to solve the issue. Maxwell predicted that the magnetic field will still exist even in the absence of conduction current, and the magnetic field may be associated with the changing electric field. This theory of Maxwell was experimentally proved. Since the magnetic field is associated with the electric field, the general displacement current formula is given by,
This equation is the generalized formula of Maxwell-Ampere law.
Displacement Current Definition The displacement current (ID) is the part which Maxwell has added to the Ampere's law. ID = ε0 ε0 = Permittivity of free space
Electric flux is the time rate change of flow of the electric field through a surface. If we take the derivative of electric flux, we get the rate of change of the electric field of a given area concerning time. |
Statement of Ampere’s circuital law (without modification). It states that the line integral of the magnetic field H around any closed path or circuit is equal to the current enclosed by the path. That is ∫ H. dL=I Let the current is distributed through the surface with a current density J Then I= This implies that Apply Stoke’s theorem to L.H.S. of equation (1) to change line integral to surface integral, That is Substituting above equation in equation(9), we get
As two surface integrals are equal only if their integrands are equal Thus, ∇ x H=J (2) This is the differential form of Ampere’s circuital Law (without modification) for steady currents. Take divergence of equation (2) ∇.(∇xH)= ∇.J As divergene of the curl of a vector is always zero, therefore ∇ .( ∇xH)=0 It means ∇.J=0 Now, this is equation of continuity for steady current but not for time varying fields, as equation of continuity for time varying fields is ∇ .J = – |
Maxwell Equations Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena. From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization. We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed. Maxwell’s four equations are given by ∇·E = ρ/ε0 (1) ∇×E = −∂B/∂t (2) ∇×H = J + ∂D/∂t (3) ∇·B = 0 (4) These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation, ∇=(∂/∂x, ∂/∂y, ∂/∂z) E is the electric vector B is the magnetic induction ρ is the electric charge density j is the electric current density ε0 is the permittivity of free space c is the speed of light. In addition to Maxwell equations, the following identities are useful:
J = σE (5) D = εE (6) B = μH (7)
Here, D is the electric displacement H is the magnetic vector σ is the specific conductivity ε is the dielectric constant (or permittivity) μ is the magnetic permeability In the Gaussian systems of units, Maxwell equations are given in the form of ∇·B=0 (8) ∇·E=4πρ (9) ∇×H=(1/c)(∂D/∂t+4πj) (10) ∇×E=−(1/c)(∂B/∂t) (11)
Free space or non-conducting medium. We know that non conducting medium means no current so conductivity is zero i.e. σ=0 So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below. (a) No condition current i.e σ=0, thus J=0 ( J=σE) (b) No charges (i.e ρ=0) For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as ∇.D=0 or ∇.E=0 as ρ=0 (12) ∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13) ∇ x H=d D/dt or ∇ x H = ε dE/dt (J=0) and D = εE (14) ∇.B=0 (15) Now taking curl of second Maxwell’s equation (13) ,we get ∇ x(∇ x E)=- μ d/dt (∇ x H) Applying standard vector identity, that is [∇ *(∇*E)=∇(∇.E)-∇2E] on left hand side of above equation, we get ∇ (∇ .E)-∇2E= -μ d/dt (∇ x H) (16) Substituting equations (13) and (14) in equations (16) ,we get -∇2E= – με d/dt (dE/dt) Or ∇2E=με d 2 E/dT2 (17) Equation (17) is the required wave equation in terms of electric field intensity, E for free space . This is the law that E must obey. Wave Equation In Terms Of Magnetic Field Intensity, H Take curl of fourth Maxwell’s equation(14) ,we get ∇x(∇xH)=ε d/dt(∇xE) Applying standard vector identity that is [∇*(∇*H)=∇ (∇.H)-∇2H] On left side of above equation , we get ∇(∇.H)-∇2H= ε d/dt(∇xE) (18) Substituting equations (14) and (13) in equation(18) ,we get -∇2H= – μεd/dt(dH/dt) Or ∇2H=με d2H/dt2 (19) Equations (19) is the required wave equation in terms of magnetic field intensity, H and this is the law that H must obey For vacuum μ=μ0 and ε=ε0, equations (17) and (19) will become ∇2 E=μ0ε0 d2E/dt2 (20) And ∇2H= μ0ε0 d2H/dt2 (21)
This leads to an expression for the velocity of propagation From equation both equations (20) and (21) have the form of the general wave equation for a wave
(x,t) traveling in the x direction with speed v. Equating the speed with the coefficients, we derive the speed of electric and magnetic waves, which is a constant that we symbolize with “c” It is useful to note that in vacuum c2=1/ε0μ0 Where μ0 is the permeability of free space
|
A wave’s energy is proportional to its amplitude squared. This is true for waves on guitar strings, for water waves, and for sound waves. In electromagnetic waves, the amplitude is the maximum field strength of the electric and magnetic fields. So the energy of electromagnetic field is proportional to its amplitude squared (E2 or B2). The electric field describes an electromagnetic wave completely in free space. The magnetic field is related to the electric field by a simple relationship. Start from Faraday's law. ∇ x E= -dB/dt From left side . Substitute the one dimensional wave equation for electricity and find its curl.
From right side, Substitute the one dimensional wave equation for magnetism and find its time derivative.
Set the two sides equal. Cancel the cosine terms and some other stuff. We will get
After Rearranging it
And we know that fλ is the speed of light. So the above equation can be written as
This knowledge can then be used to simplify the energy density situation a bit. Start with the magnetic energy density and replace it with an expression containing the electric field.
Recall that the speed of light is related to the permeability and permittivity constants. c = So
Thus ηB = It's the electric energy density. For an electromagnetic wave in free space, half the energy is in the electric field and half is in the magnetic field η = ηE + ηB η = This gives us this compact equation for the total energy density of an electromagnetic wave. η = ε0E2 or this one, if you prefer to state things in terms of the magnetic field instead η = This is an interesting and simple set of relations, but keeps in mind that it only works for electromagnetic waves in free space. Things are different in a media and the electric and magnetic fields can have any values they want if they're static (meaning there's no accelerating charges). Since waves are spread out in space and time, energy density is often a more useful concept than energy. |
When electromagnetic wave travels in space, it carries energy and energy density is always associated with electric fields and magnetic fields. The rate of energy travelled through per unit area i.e. the amount of energy flowing through per unit area in the perpendicular direction to the incident energy per unit time is called Poynting vector. Mathematically Poynting vector is represented as
The direction of Poynting vector is perpendicular to the plane containing UNIT Its unit is W/m2. Poynting Theorem Poynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses. i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of charge Proof The energy density carried by the electromagnetic wave can be calculated using Maxwell's equations div div Curl Curl Taking scalar product of (3) with H and (4) with i.e. and Doing (vi) – (v) i.e.
So from equation (vii)
Or
Integrating equation (viii) over a volume V enclosed by a Surface S
Total power leaving the volume = rate of decrease of stored e.m. energy -ohmic power dissipated due to charge motion This equation (ix) represents the Poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses. In equation (ix) The term represents
the energy stored in electric and magnetic fields respectively and their sum denotes the total energy stored in electromagnetic field. So total terms gives the rate of decrease of energy stored in volume V due to electric and magnetic fields.
Gives the rate of energy transferred into the electromagnetic field. This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism. |
In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature. Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis. A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts. In this section we will study the variation of field of Variation With Space First we will consider the variation with space. Suppose a plane em wave is propagating along x axis. Then the values of the field vectors For
For
From Maxwell’s equation for free space, we have ∇.E=0 Therefore
Which gives
Also From Maxwell’s equation for free space, we have ∇.B=0 we have ∇.H=0 as B = μH Hence
Which gives The equation (3) and (4) show that there is no variation of Time Variation of The Maxwell’s equation in free space can be written as: ∇ x E= -dB/dt or ∇ x E= -μ Comparing the rectangular components, we find:
Applying the condition listed in equation (1), from equation (5), we find:
Again using Maxwell’s equation for free space is: ∇ x H= Comparing the rectangular components, we can write:
Again using the conditions listed in equation (2) gives:
From equation (8) and (12), we find that there is no variation in the values of Now from equation 6 and 7 by putting
Similarly putting
These relations show that in the em values |
We know that wave equations are given by ∇2 E=με d2E/dt2 …………..(1) And ∇2H= με d2H/dt2 …………..(2) The electric and magnetic vectors in an em waves are given by:
It is evident therefore that:
and
Substitute the values of -ik E0eik (vt-x) =- μ (ikv) H0eik (vt-x) Which gives E0 =- μvH0 But v = E0 = μ x E0 =
That is the relation between the values of the electric and magnetic vectors as determined by the relative values μ and Ɛ. In other words, the ratio of the electric and magnetic vectors is directly proportional to the square root of the ratio of μ and Ɛ.
E0 =377 H0 or E =377H It shows that the values of electric vector at any instant in the em wave are about 377 times the values of magnetic vector. It is because of this reason that while discussing the behaviour of light as em wave, we prefer the use of the electric vector. |
In a region of empty space where u= For electromagnetic waves in a vacuum, B = B= It follows that: u=Ɛ0E2 In a vacuum, the energy density associated with the field. In general, the energy density u of an electromagnetic wave depends on position and time. Electromagnetic waves transport energy from one region to another – they carry the energy density u with them as they advance. Consider a stationary plane, perpendicular to the x-axis, that coincides with the wave front at a certain time. In a time dt after this, the wave front moves a distance dx=cdt to the right of the plane. Consider an area A on this stationary plane, the energy dU in the space to the right of this area must have passed through the area to reach the new location. Hence, dU = udV = ( Ɛ0E2) (Acdt) The energy flow per unit time per unit area is given by: S = = Ɛ0c2E ( = The energy flow per unit time per unit area has a term attached to it: Poynting vector S = The total energy flow per unit time out of any closed surface is given by: P=∮ Let’s calculate the Poynting vector for typical sinusoidal waves:
The intensity of the radiation is the magnitude of the average value of the Poynting vector.
Electromagnetic waves also carry momentum p, with a corresponding momentum density. Let’s calculate the momentum carried by electromagnetic waves by using the well-known relativistic formula: E2=p2c2+m2c4. According to quantum mechanics, the electromagnetic radiation is made up of massless particles called photons, with momentum p=Ec for individual photons. It follows from p=E/c that the momentum density for electromagnetic waves must be equal to the energy density divided by c. Since the energy density for electromagnetic waves is given by: u= Ɛ0cE2
We can further express the above as momentum transferred per unit time per unit area:
This momentum is a property of the field – it is not associated with the mass of a moving particle in the usual sense. This momentum is responsible for the phenomenon of radiation pressure. If an electromagnetic wave with an average value of Poynting vector of Sav is incident on an object, with no reflection and transmission, the radiation pressure on the object will be given by: prad is radiation pressure and dp is the infinitesimal change in momentum. prad =
If all of the incident electromagnetic waves are reflected by the object, the resulting radiation pressure will be: prad = |
We know that amplitude of the em wave decreases exponentially with distance of penetration of the wave. Suppose, the amplitude at a depth x is denoted by Ex. Then Ex = E0e-kx ………….(1) Where k = [ The decrease in amplitude or attenuation of the field vector is quantitatively expressed in terms of a quantity called skin depth. It is defined as the distance beyond the surface of the conductor inside it at which the amplitude of the field vector is reduced to 1/e of its value at the surface. Let the skin depth is denoted by Eδ = Where E0 = amplitude vector at the surface of the conductor Eδ = amplitude of electric vector at depth So equation (3) can be written as
k
It shows that the skin depth varies inversely as the square root of conductivity of the medium and frequency of em wave. Example: Calculate the skin depth for a frequency of 1010 Hz for silver. Given that Solution:
Example: Find the skin depth of copper if Solution: Given
n =50 Hz ω = 2πn =2 x 3.14 x 50 = 314.3
|
Reference Books
1. Concepts of Modern Physics - AurthurBeiser (Mc-Graw Hill)
2. Introduction to Special Theory of Relativity- Robert Resnick (Wiley)
3. Optics - Brijlal& Subramanian (S. Chand )
4. Engineering Physics: Theory and Practical- Katiyar and Pandey (Wiley India)
5. Applied Physics for Engineers- Neeraj Mehta (PHI Learning, New)
6. Engineering Physics-Malik HK and Singh AK (McGrawHill)