Unit-1
Ordinary Differential Equation of Higher Order
A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,
The form of second order linear differential equation with constant coefficients is,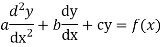
Where a,b,c are the constants.
Let, aD²y+bDy+cy = f(x), where d² = 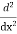 , D =
, D = 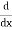
∅(D)y = f(x) , where ∅(D)y = aD²y+bDy+cy
Here first we solve, ∅(D)y = 0, which is called complementary function (C.F)
Then we find particular integral (P.I)
P.I. = 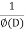 f(x)
f(x)
General solution = C.F. +P.I.
Let’s do an example to understand the concept,
Example1: Solve (4D² +4D -3)y = 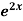
Solution: Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m =  ,
, 
Complementary function: CF is A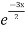 + B
+ B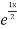
Now we will find particular integral,
P.I. = 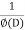 f(x)
f(x)
= 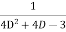 .
. 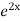
= 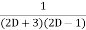 .
. 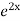
= 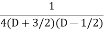 .
. 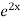
= 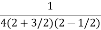 .
. 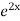 =
= 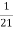 .
. 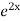
General solution is y = CF + PI
= A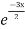 + B
+ B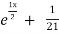 .
. 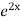
Differential operators-
D stands for operation of differential i.e.
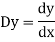
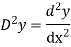
 stands for the operator of integration.
stands for the operator of integration.
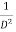 stands for operation of integration twice.
stands for operation of integration twice.
Thus,
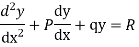
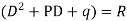
Note:-
Complete solution = complementary function + Particular integral
I.e. y=CF + PI
Method for finding the CF
Step1:- In finding the CF right hand side of the given equation is replaced by zero.
Step 2:- Let 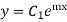 be the CF of
be the CF of
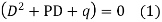
Putting the value of 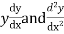 in equation (1) we get
in equation (1) we get

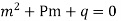
It is called auxiliary equation.
Step 3:- Roots Real and Different
If 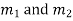 are the roots the CF is
are the roots the CF is 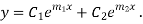
If 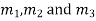 are the roots then
are the roots then 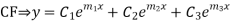
Step 4- Roots Real and Equal
If both the roots are 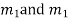 then CF is
then CF is
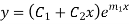
If roots are 
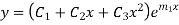
Example: Solve 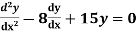
Ans. Given, 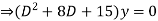
Here Auxiliary equation is
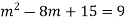
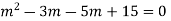
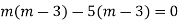
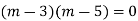
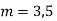
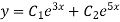
Example: Solve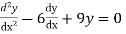
Or,
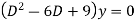
Ans. Auxiliary equation are 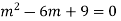
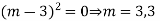
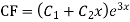
Note: If roots are in complex form i.e. 
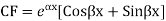
Example: Solve 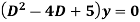
Ans. Auxiliary equation is 
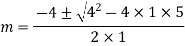
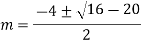

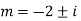

Rules to find Particular Integral
Case 1: 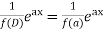
If, 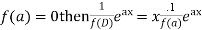
If, 
Example: Solve 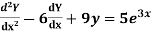
Ans. Given, 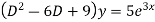
Auxiliary equation is 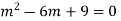
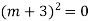
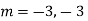
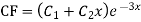

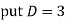
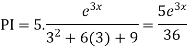
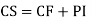
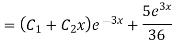
Case2: 
Expand 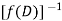 by the
by the
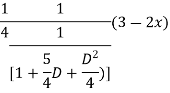

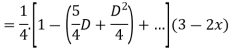
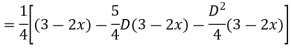
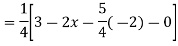

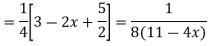
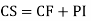
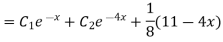
Case 3: 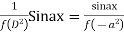
Or,
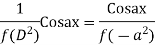
Example: 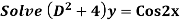
Ans. Auxiliary equation are 
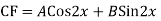

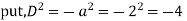
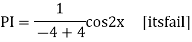
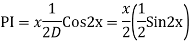
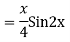
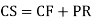
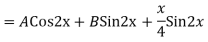
Case 4: 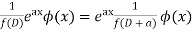
Example: Solve 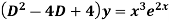
Ans. AE= 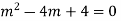
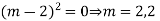
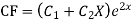
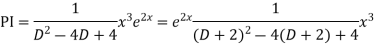
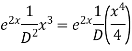
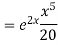
Complete solution is 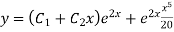
Example: Solve 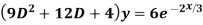
Ans. The AE is 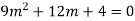
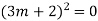
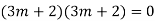
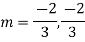
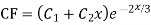
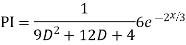
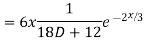
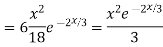
Complete solution y= CF + PI
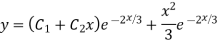
Example: Solve 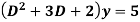
Ans. The AE is 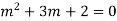
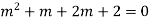
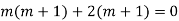
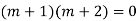
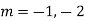
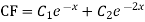
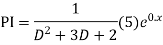
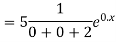
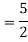
Complete solution = CF + PI
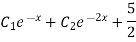
Example: Solve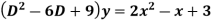
Ans. The AE is 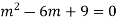
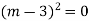
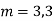
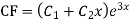
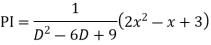
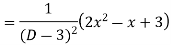
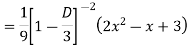
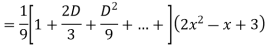
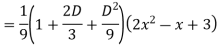
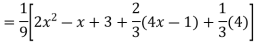
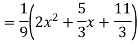
Complete solutio0n is y= CF + PI
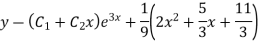
Example: Find the PI of 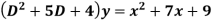
Ans. 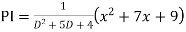
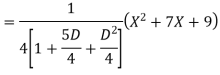
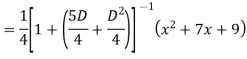



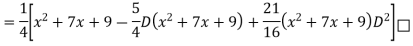
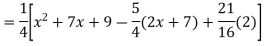

Example: solve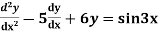
Ans. Given equation in symbolic form is
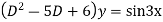
Its Auxiliary equation is 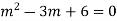
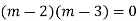
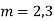
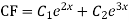
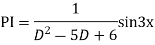
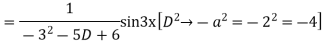
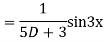
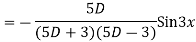
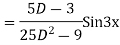
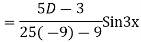
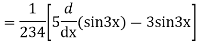
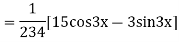
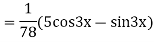
Complete solution is y= CF + PI

Example: Solve
Ans. The AE is 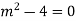
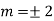
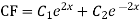
We know, 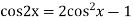
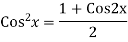
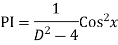
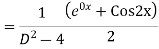
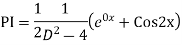

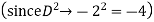

Complete solution is y= CF + PI
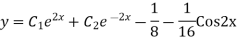
Example: Find the PI of(D2-4D+3)y=ex cos2x
Ans. 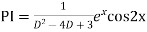

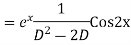
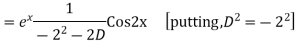

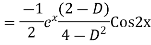
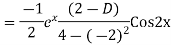
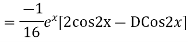
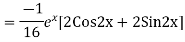
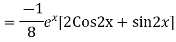
Example. Solve(D3-7D-6) y=e2x (1+x)
Ans. The auxiliary equation i9s
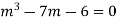
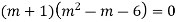
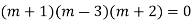
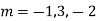
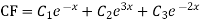

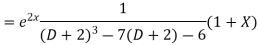
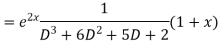

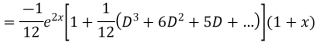
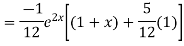
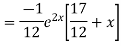
Hence complete solution is y= CF + PI
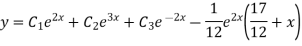
Key takeaways-
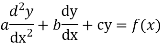
Where a,b,c are the constants.
2. General solution = C.F. +P.I.
3. 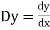
4. 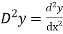
5. Roots Real and Equal-
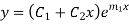
6. Roots Real and Different-
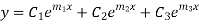
7. If roots are in complex form i.e. 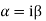
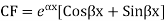
The equation involving the derivatives of two or more dependent variables, which are the functions of a single independent variable, the equations involving their derivative is called simultaneous equation.
Such as-
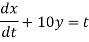
We use method of elimination to solve these types of equations.
Example 1: Solve the following simultaneous differential equations-

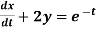 ....(2)
....(2)
Solution:
Consider the given equations
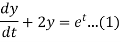
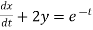 ....(2)
....(2)
Consider eq(1),(2)
Dx+2y = et....(1)
Dx +2x =e-t....(2)
Eliminating ‘x’ from both the equations we get,
1 2
2 2Dx + 2y = 2et
2Dx + 2y = 2et
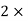 D
D 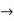 2Dx +D2y = e-t
2Dx +D2y = e-t
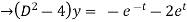
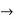 y = Ae2t + Be-2t +
y = Ae2t + Be-2t + 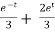
Example 2: Solve the following simultaneous differential equations-
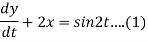
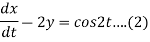
Given that x(0)=1 and y(0)= 0
Solution:
Consider the given equations,
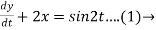 Dy +2x = sin2t
Dy +2x = sin2t
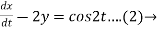 Dx -2y = cos2t
Dx -2y = cos2t
By solving the above equations, we get,
(D2 +4)Y =0
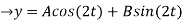
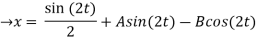
X(0) = 1, y(0) = 0
 A =0, B=-1
A =0, B=-1
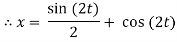
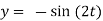
Example-3: Solve the following simultaneous differential equations-
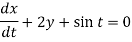
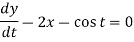
It is given that x = 0 and y = 1 when t = 0.
Sol. Given equations can be written as-
Dx + 2y = - sin t ………. (1) and -2x + Dy = cos t ……… (2)
Eliminate x by multiplying (1) by 2 and (2) by D then add-
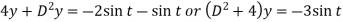
Here A.E = 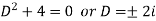
So that C.F. = 
And P.I. = 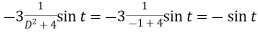
So that- 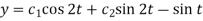 …………. (3)
…………. (3)
And 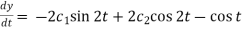 ………….. (4)
………….. (4)
Substitute (3) in (2), we get-
2x = Dy – cos t = 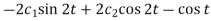
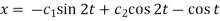 ………… (5)
………… (5)
When t = 0, x = 0, y = 1. (3) and (5) gives- 
Hence 
Linear differential equation are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus the general linear differential equation of the n’th order is of the form
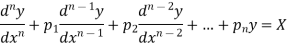
Where  and X are function of x.
and X are function of x.
Linear differential equation with constant co-efficient are of the form-

Where 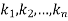 are constants.
are constants.
Rules to find the complementary function-
To solve the equation-

This can be written as in symbolic form-
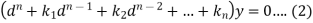
Or-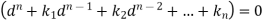
It is called the auxiliary equation.
Let 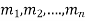 be the roots-
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,
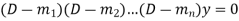
Now this equation will be satisfied by the solution of 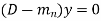
This is a Leibnitz’s linear and I.F. = 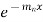
Its solution is-
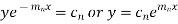
The complete solution will be-
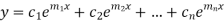
Case-2: If two roots are equal 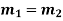
Then complete solution is given by-
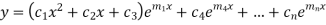
Case-3: If one pair of roots be imaginary, i.e.  then the complete solution is-
then the complete solution is-
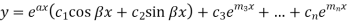
Where 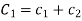 and
and 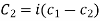
Case-4: If two points of imaginary roots be equal-
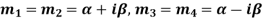
Then the complete solution is-

Example-Solve 
Sol.
Its auxiliary equation is-
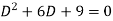
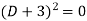
Where-
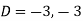
Therefore, the complete solution is-
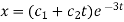
Inverse operator-
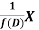 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
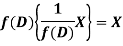
So that 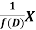 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 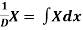
2. 
Rules for finding the particular integral-
Let us consider the equation-
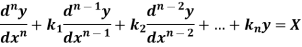
Or in symbolic form-
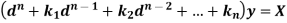
So that-
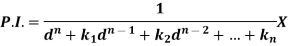
Now-
Case-1: When X = 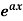
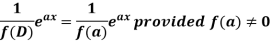
In case f(a) = 0, then we see that the above rule will not work,
So that-

Example: Find the P.I. of (D + 2)
Sol.
P.I. = 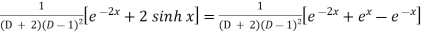
Now we will evaluate each term separately-
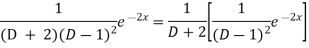
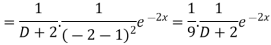
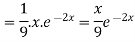

And

Therefore-
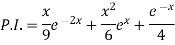
Example: Solve (D – D’ – 2 ) (D – D’ – 3) z = 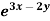
Sol.
The C.F. will be given by-

Particular integral-
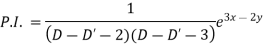

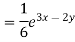
Therefore the complete solution is-
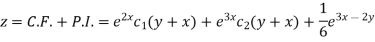
Case-2: when X = sin(ax + b) or cos (ax + b)
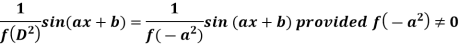
In case 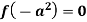 then the above rule fails.
then the above rule fails.
Now-

And if 
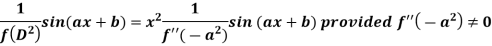
Similarly-
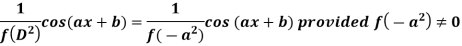
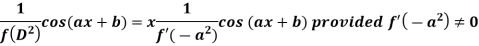
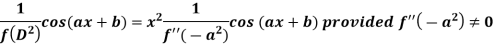
Example: Find the P.I. of 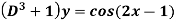
Sol.
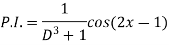

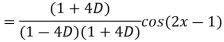
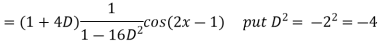
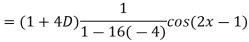
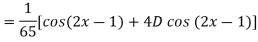
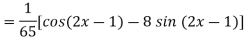
Example: Find the P.I. of (D + 1) (D + D’ – 1)z = sin (x + 2y)
Sol.
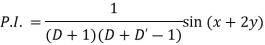
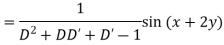
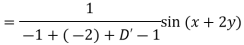
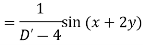
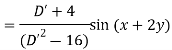
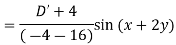
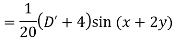
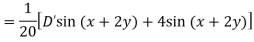
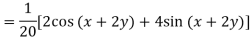
Example: Find P.I. of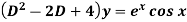
Sol. P.I = 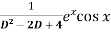
Replace D by D+1
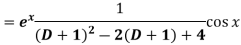
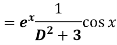
Put 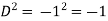
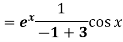
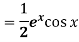
Key takeaways-
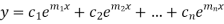
2. If two roots are equal 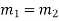 Then complete solution is given by-
Then complete solution is given by-
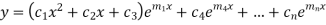
3. If one pair of roots be imaginary, i.e. 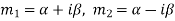 then the complete solution is-
then the complete solution is-
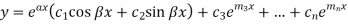
Where 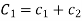 and
and 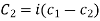
4. If two points of imaginary roots be equal-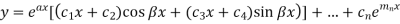
Let
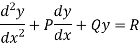
Be the differential equation where P, Q, R are the functions of x.
If y = u(x) is the solution we know, then put y = uv in it.
It reduces the diff. Equation to one of first order in dv/dx which can be solved completely.
Note-
1 if 1+P+Q = 0, Then 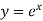 is a solution.
is a solution.
2. if 1-P+Q = 0, Then 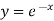 is a solution.
is a solution.
3. if P+Qx = 0, Then 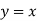 is a solution.
is a solution.
Example: Solve
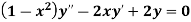
It is given that y = x is a solution.
Sol.
Suppose y = xv so that-
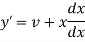
And
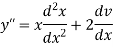
Now put these values in the given equation, we get-
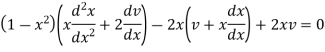
Or

Or
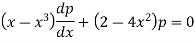
Where p = dv/dx
On integrating, we get-
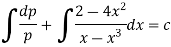
Or
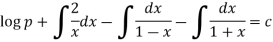

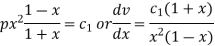
Again integrating,
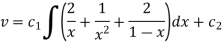
Or
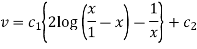
Hence the required solution-

Equation which can be solved by changing the independent variable-
Consider the equation-

Lets change the independent variable x to z and z = f(x)
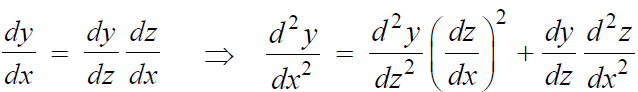
Now put these values in the equation, we get-

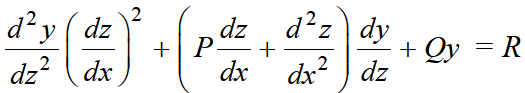
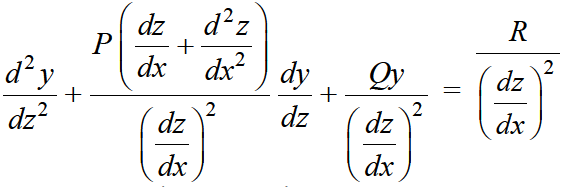
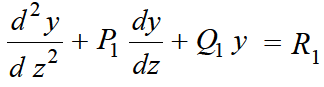 ........ (1)
........ (1)
here
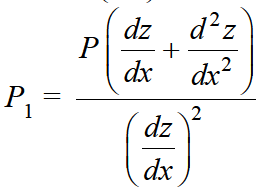 ,
, 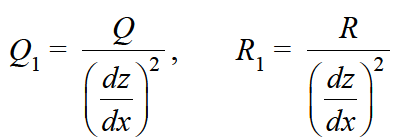
Equation-1 can be solved by taking 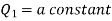
Example: Solve-
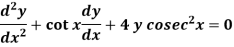
Sol.
Here P = cot x and Q = 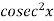
Choosing z so that
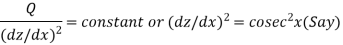

Changing the independent variable x to z, we get-
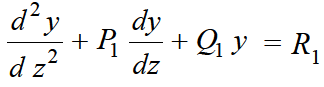 ......(1)
......(1)
Where-

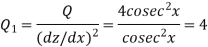

Equation(1) becomes-

Its sol. Is-
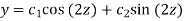
i.e.
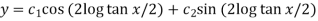
Which is the required solution
Key takeaways-
1 if 1+P+Q = 0, Then 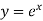 is a solution.
is a solution.
2. if 1-P+Q = 0, Then  is a solution.
is a solution.
3. if P+Qx = 0, Then 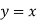 is a solution
is a solution
Let  is known non-trivial solution of the second order homogeneous linear equation-
is known non-trivial solution of the second order homogeneous linear equation-
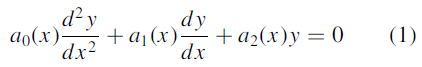
Then the second linearly independent non-trivial solution
 of (1) can be obtained by the method
of (1) can be obtained by the method
Of reduction of order. This method makes use of a
Transformation of the form
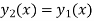

which reduces the second order equation (1) to a first
order differential equation which is then integrate for
the unknown function v(x).
write again (1) in the standard form
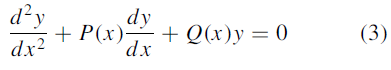
Where P(x) = 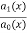 , Q =
, Q =  with
with 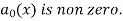
Differentiating (2) w.r.t. x, we get-
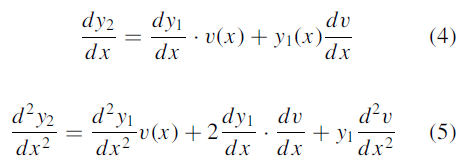
Put (2), (4), (5) in (3), we get-

Rewriting-
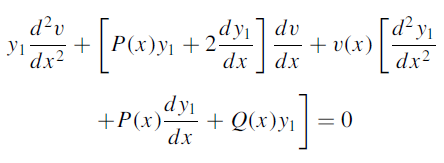
Here  is a known solution of (1), then the last term in above equation becomes zero.
is a known solution of (1), then the last term in above equation becomes zero.
Let introduce-
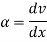
the above equation reduces to a first order
linear differential equation in the new dependent
variable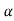 , given by
, given by

Separating the variables and integrating, we get
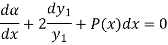
Or

Then-
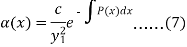
Choosing, c = 1

Now on integrating-
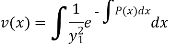
So that we get the required second solution 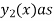 -
-
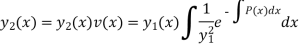
Hence  from the basis of diff equation (1) and general solution of (1) is-
from the basis of diff equation (1) and general solution of (1) is-
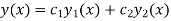
Example: Obtain the basis for the equation 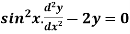 if
if 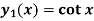 is a solution.
is a solution.
Sol.
The standard form of the equation will be-
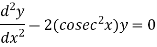
So that-
P(x) = 0. The 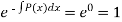
Now-
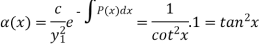
So-
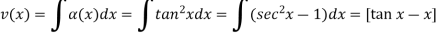
Then
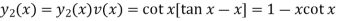
The basis consisting of the two linearly independent solutions is-

Example on normal norm-
Example: Solve 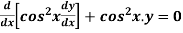
Sol.
Here we have-
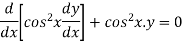
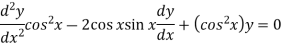
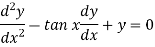
Here,
P = -2 tan x, Q = 1, R = 0
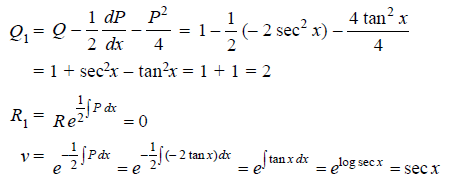
Normal equation is-
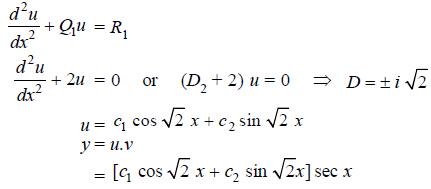
Example: Solve 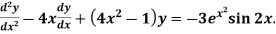
Sol.
Here we have-
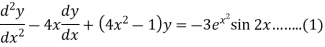
Here p = -4x, Q = 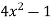 , R =
, R = 
Now in order to remove the first derivative x,
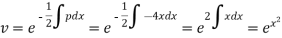
Now on putting y = uv, then normal equation is-
 .............(2)
.............(2)
Where
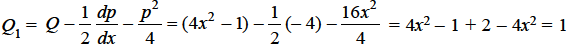
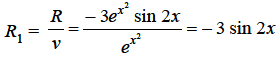
Equation (2) becomes-
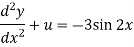
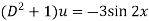
Auxiliary equation-
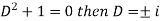
C.F.-
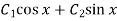

Method of variation of parameters-
Consider a second order LDE with constant co-efficients given by

Then let the complimentary function 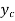 is given by
is given by
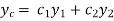
Then the particular integral is
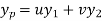
Where u and v are unknown and to be calculated using the formula
u=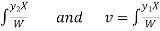
Example-1: Solve the following DE by using variation of parameters-

Sol. We can write the given equation in symbolic form as-

To find CF-
It’s A.E. is 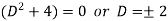
So that CF is- 
To find PI-
Here 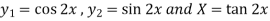
Now 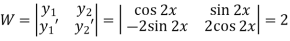
Thus PI = 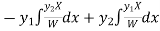
= 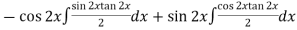
= 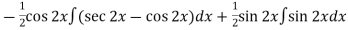
= 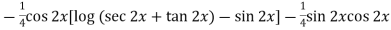
= 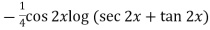
So that the complete solution is-
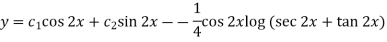
Example-2: Solve the following by using the method of variation of parameters.
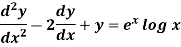
Sol. This can be written as-
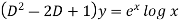
C.F.-
Auxiliary equation is- 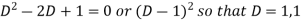
So that the C.F. will be- 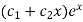
P.I.-
Here 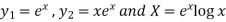
Now 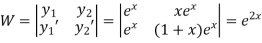
Thus PI = 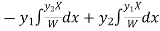
= 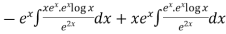
= 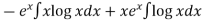
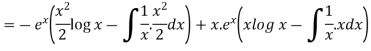
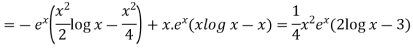
So that the complete solution is-
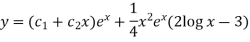
An equation of the form
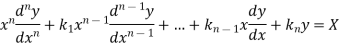
Here X is the function of x, is called Cauchy’s homogeneous linear equation.
Example-1: Solve 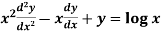
Sol. As it is a Cauchy’s homogeneous linear equation.
Put 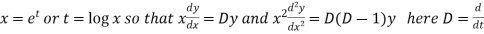
Then the equation becomes [D(D-1)-D+1]y = t or 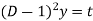
Auxiliary equation-
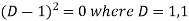
So that-
C.F.=
Hence the solution is- 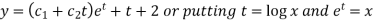 , we get-
, we get-
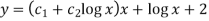
Example-2: Solve 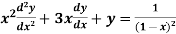
Sol. On putting 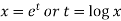 so that,
so that,
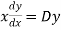 and
and 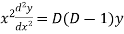
The given equation becomes-

Or it can be written as-

So that the auxiliary equation is- 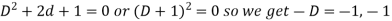
C.F. = 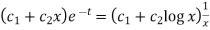
Particular integral- 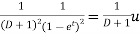
Where 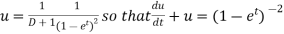
It’s a Leibnitz’s linear equation having I.F.=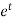
Its solution will be-
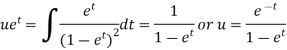
P.I. = 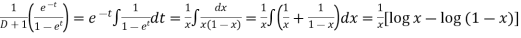
= 
So that the complete solution is-

An equation of the form-

Is called Legendre’s linear equation.
Example-3: Solve 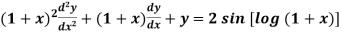
Sol. As we see that this is a Legendre’s linear equation.
Now put 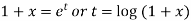
So that- 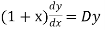
And 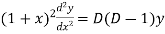
Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t
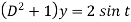
Its auxiliary equation is- 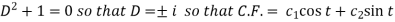
And particular integral-
P.I. = 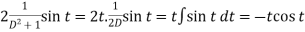
Note - 
Hence the solution is - 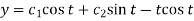
Key takeaways-
Cauchy’s homogeneous linear equation-

We know that the solution of the differential equation-
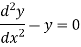
Are
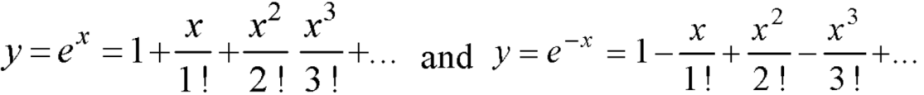
These are the power series solutions of the given differential equations.
Ordinary Point-
Let us consider the equation-
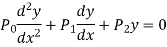
Here 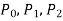 are polynomial in x.
are polynomial in x.
X = a is an ordinary point of the above equation if  does not vanish for x = a.
does not vanish for x = a.
Note- If 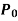 vanishes for x = a, then x = a is a singular point.
vanishes for x = a, then x = a is a singular point.
Solution of the differential equation when x = 0 is an ordinary point, which means 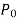 does not vanish for x = 0.
does not vanish for x = 0.
1. Let 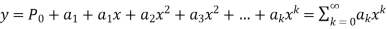 be the solution of the given differential equation.
be the solution of the given differential equation.
2. Find 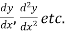
3.
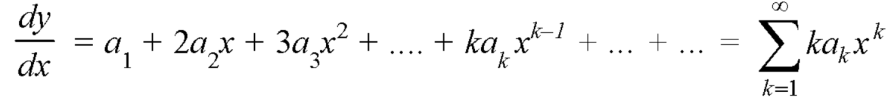

4. Substitute the expressions of y, 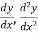 etc. in the given differential equations.
etc. in the given differential equations.
5. Calculate 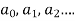 Coefficients of various powers of x by equating the coefficient to zero.
Coefficients of various powers of x by equating the coefficient to zero.
6. Put the values of 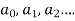 In the differential equation to get the required series solution.
In the differential equation to get the required series solution.
Example- Solve
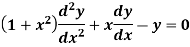
Sol.
Here we have-

Let the solution of the given differential equation be-
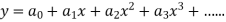
Since x = 0 is the ordinary point of the given equation-
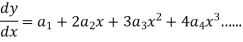
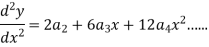
Put these values in the given differential equation-
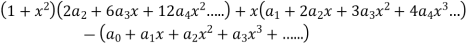
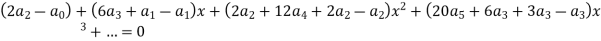
Equating the coefficients of various powers of x to zero, we get-
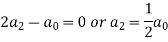
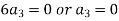
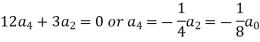
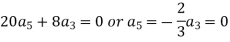
Therefore the solution is-
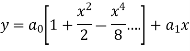
Example: Solve in series the equation-
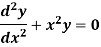
Sol.
Here we have-
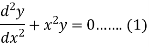
Let us suppose-
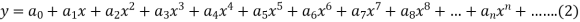
Since x = 0 is the ordinary point of (1)-
Then-
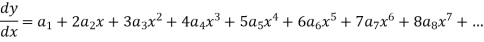
And
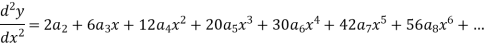
Put these values in equation (1)-
We get-
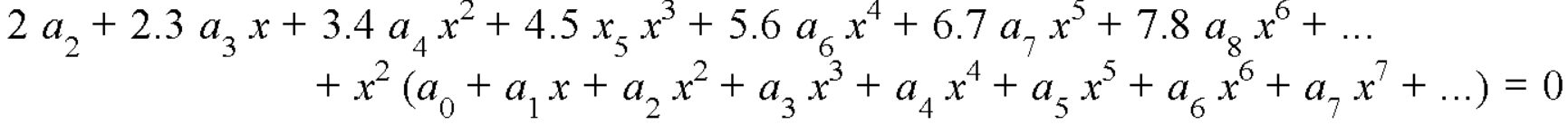
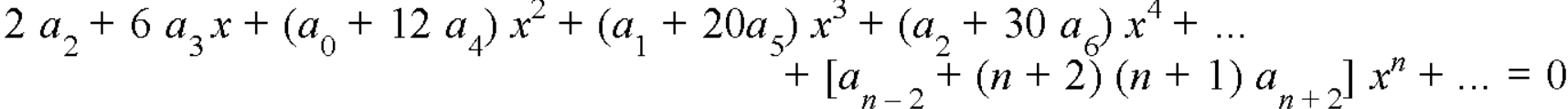
Equating to zero the coefficients of the various powers of x, we get-
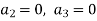
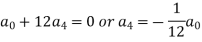
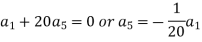
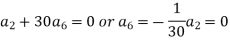
And so on….
In general we can write-
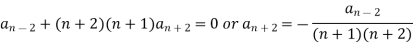
Now putting n = 5,
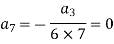
Put n = 6-
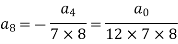
Put n = 7,
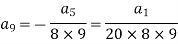
Put n = 8,
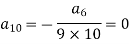
Put n = 9,
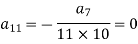
Put n = 10,
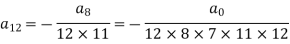
Put the above values in equation (1), we get-
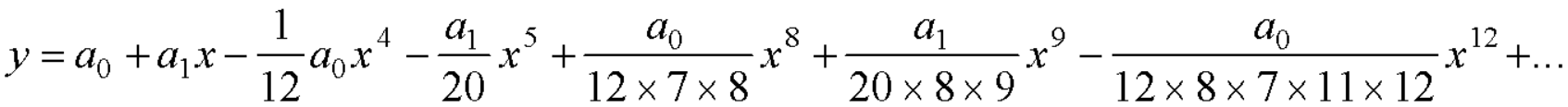
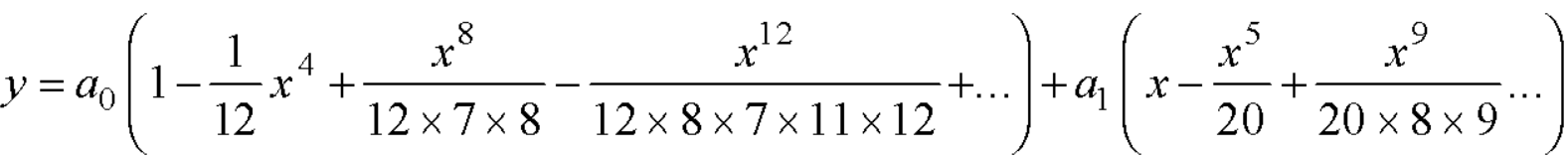
Frobenius method-
This method is also called generalized power series method.
If x = 0 is a regular singularity of the equation.
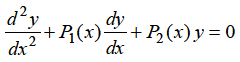 ……..(1)
……..(1)
Then the series solution is-
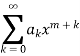
Which is called Frobenius series.
On equating the coefficient of lowest power of x in the identity to zero, we get a quadratic equation in ‘m’.
We will get two values of m. The series solution of (1) will depend on the nature of the roots of the indicial equation-
Case-1: when roots m1 and m2 are distinct and these are not differing by an integer-
The complete solution in this case will be-
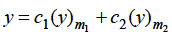
Case-2: when roots m1 and m2 are equal-
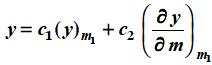
Case-3: when roots are distinct but differ by an integer-
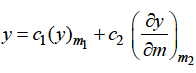
Case-4: Roots are distinct and differing by an integer, making some coefficient indeterminate-
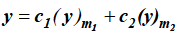
Example: Find solution in generalized series form about x = 0 of the differential equation
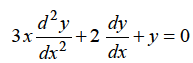
Sol.
Here we have
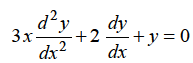 ………… (1)
………… (1)
Since x = 0 is a regular singular point, we assume the solution in the form
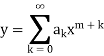
So that
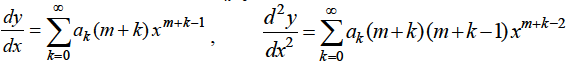
Substituting for y, 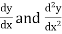 in equation (1), we get-
in equation (1), we get-
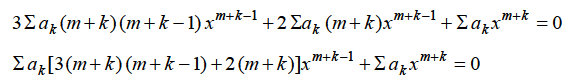 …..(2)
…..(2)
The coefficient of the lowest degree term 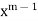 in (2) is obtained by putting k
in (2) is obtained by putting k
= 0 in first summation only and equating it to zero. Then the indicial equation is
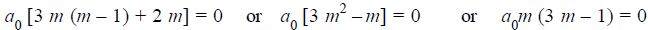
Since 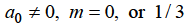
The coefficient of next lowest degree term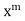 in (2) is obtained by putting
in (2) is obtained by putting
k = 1 in first summation and k = 0 in the second summation and equating it to zero.
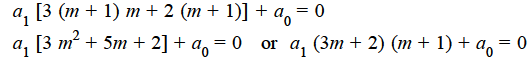
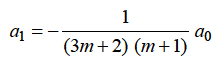
Equating to zero the coefficient of the recurrence relation is given by
the recurrence relation is given by
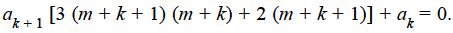
Or
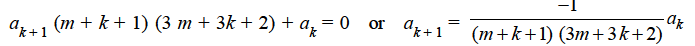
Which gives-
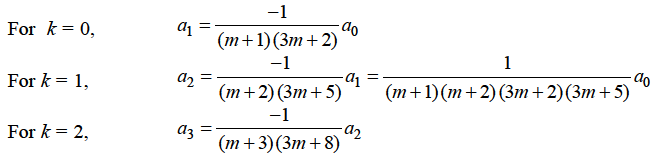
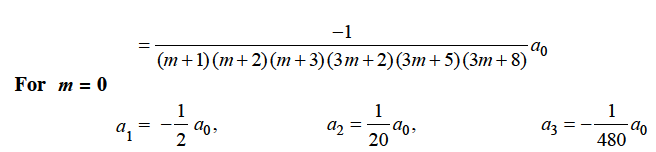
Hence for-
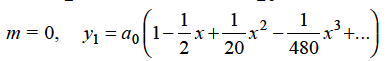
Form m = 1/3-
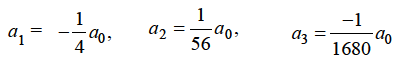
Hence for m = 1/3, the second solution will be-
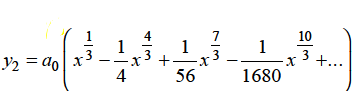
The complete solution will be-
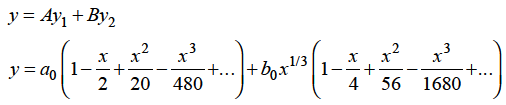
Key takeaways-

If x = 0 is a regular singularity of the equation.
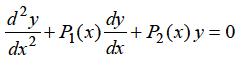 ……..(1)
……..(1)
Then the series solution is-

Which is called Frobenius series.
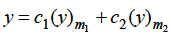
2. When roots m1 and m2 are equal-
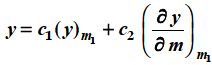
3. When roots are distinct but differ by an integer-
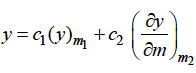
4. Roots are distinct and differing by an integer, making some coefficient indeterminate-

References