Unit – 3
Searching
Searching
Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful and the process returns the location of that element, otherwise the search is called unsuccessful.
There are two popular search methods that are widely used in order to search some items into the list. However, the choice of the algorithm depends upon the arrangement of the list.
● Linear Search
● Binary Search
Linear search
Linear search, often known as sequential search, is the most basic search technique. In this type of search, we simply go through the entire list and match each element to the item whose position has to be discovered. If a match is found, the algorithm returns the item's location; otherwise, NULL is returned.
Binary search
Binary search is a search technique that performs well on sorted lists. As a result, in order to use the binary search strategy to find an element in a list, we must first confirm that the list is sorted.
The divide and conquer strategy is used in binary search, in which the list is divided into two halves and the item is compared to the list's middle element.
A linear or sequential relationship exists when data objects are stored in a collection, such as a list. Each data item is kept in a certain location in relation to the others. These relative positions are the index values of the various items in Python lists. We can access these index values in order because their values are ordered. Our initial searching strategy, the sequential search, is born out of this procedure.
This is how the search works, as shown in the diagram. We just advance from item to item in the list, following the underlying sequential ordering, until we either find what we're looking for or run out of options. If we run out of items, we have discovered that the item we were searching for was not present.
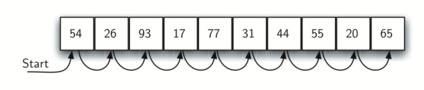
Fig 1: Sequential search
Algorithm
● LINEAR_SEARCH(A, N, VAL)
● Step 1: [INITIALIZE] SET POS = -1
● Step 2: [INITIALIZE] SET I = 1
● Step 3: Repeat Step 4 while I<=N
● Step 4: IF A[I] = VAL
SET POS = I
PRINT POS
Go to Step 6
[END OF IF]
SET I = I + 1
[END OF LOOP]
● Step 5: IF POS = -1
PRINT " VALUE IS NOT PRESENTIN THE ARRAY "
[END OF IF]
● Step 6: EXIT
Time complexity
Best case - O(1)
Average case - O(n)
Worst case - O(n)
Space complexity
Worst case - O(1)
Indexed sequential search is another strategy for improving search efficiency for a sorted file. However, it necessitates a larger quantity of memory space. In addition to the sorted file, an index table is kept aside. Each index table element has a key Kindex and a link to the record in the field that matches the kindex. The index elements, as well as the file elements, must be sorted on the file.
When using this method, an index file is first constructed, which contains a specific group or division of the desired record. Once the index is obtained, partial indexing takes less time because it is situated in a specific group.
The advantage of the indexed sequential method is that even though all entries in the file must be read, items in the table can be inspected sequentially, and the search time for specific items is decreased. Rather than searching the large table, a sequential search is done on the smaller index. After finding the index point, the search is moved to the record table itself.
The easiest way to delete entries from an indexed sequential table is to mark them as deleted. Deleted items are disregarded when searching sequentially. From the original table, the item is removed.
Insertion into an indexed sequential table can be challenging since there may be no space between two table entries, resulting in a significant number of components being shifted.
Characteristics of indexed sequential search
- In Indexed Sequential Search, in addition to the array, a sorted index is created.
- Each index element refers to a block of elements in the array or to another expanded index.
- The index is searched first, followed by the array, and the array search is guided by the index.
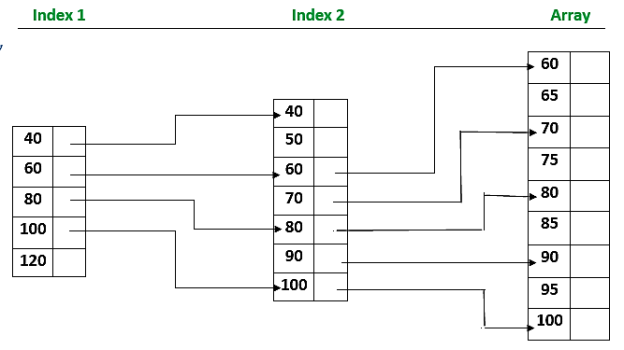
Fig 2: Indexed sequential search
Key takeaway
- Indexed Sequential Search actually does the indexing multiple times, like creating the index of an index.
- When a user requests specific records, the user's request will be directed to the index group where that specific record is stored first.
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows a divide and conquer approach in which the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned; otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
● Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1
● Step 2: Repeat Steps 3 and 4 while BEG <=END
● Step 3: SET MID = (BEG + END)/2
● Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
● Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
● Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step :
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
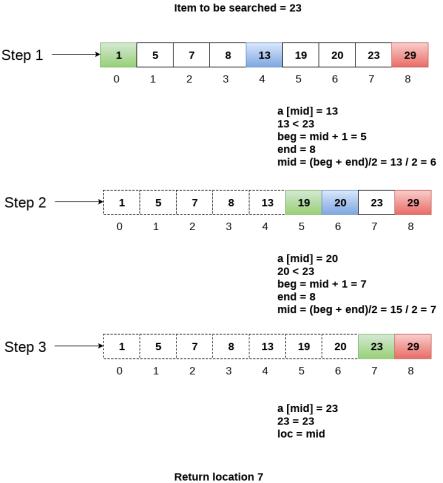
Fig 3 - Example
● Hashing is the process of mapping a large amount of data item to a smaller table with the help of hashing function.
● Hashing is also known as the Hashing Algorithm or Message Digest Function.
● It is a technique to convert a range of key values into a range of indexes of an array.
● It is used to facilitate the next level searching method when compared with the linear or binary search.
● Hashing allows the user to update and retrieve any data entry in a constant time O(1).
● Constant time O(1) means the operation does not depend on the size of the data.
● Hashing is used with a database to enable items to be retrieved more quickly.
● It is used in the encryption and decryption of digital signatures.
Hash Function
● A fixed process converts a key to a hash key is known as a Hash Function.
● This function takes a key and maps it to a value of a certain length which is called a Hash value or Hash.
● Hash value represents the original string of characters, but it is normally smaller than the original.
● It transfers the digital signature and then both hash value and signature are sent to the receiver. Receiver uses the same hash function to generate the hash value and then compares it to that received with the message.
● If the hash values are the same, the message is transmitted without errors.
Hash Table
● Hash table or hash map is a data structure used to store key-value pairs.
● It is a collection of items stored to make it easy to find them later.
● It uses a hash function to compute an index into an array of buckets or slots from which the desired value can be found.
● It is an array of list where each list is known as bucket.
● It contains value based on the key.
● Hash tables are used to implement the map interface and extend the Dictionary class.
● Hash tables are synchronized and contain only unique elements.
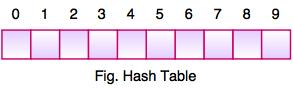
● The above figure shows the hash table with the size of n = 10. Each position of the hash table is called a Slot. In the above hash table, there are n slots in the table, names = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Slot 0, slot 1, slot 2 and so on. Hash tables contain no items, so every slot is empty.
● As we know, the mapping between an item and the slot where the item belongs in the hash table is called the hash function. The hash function takes any item in the collection and returns an integer in the range of slot names between 0 to n-1.
● Suppose we have integer items {26, 70, 18, 31, 54, 93}. One common method of determining a hash key is the division method of hashing and the formula is:
Hash Key = Key Value % Number of Slots in the Table
● Division method or reminder method takes an item and divides it by the table size and returns the remainder as its hash value.
Data Item | Value % No. Of Slots | Hash Value |
26 | 26 % 10 = 6 | 6 |
70 | 70 % 10 = 0 | 0 |
18 | 18 % 10 = 8 | 8 |
31 | 31 % 10 = 1 | 1 |
54 | 54 % 10 = 4 | 4 |
93 | 93 % 10 = 3 | 3 |
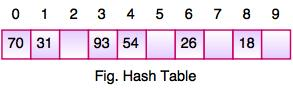
● After computing the hash values, we can insert each item into the hash table at the designated position as shown in the above figure. In the hash table, 6 of the 10 slots are occupied; it is referred to as the load factor and denoted by, λ = No. Of items / table size. For example , λ = 6/10.
● It is easy to search for an item using the hash function where it computes the slot name for the item and then checks the hash table to see if it is present.
● Constant amount of time O(1) is required to compute the hash value and index of the hash table at that location.
Collision Resolution Techniques
Collision in hashing
- In this, the hash function is used to compute the index of the array.
- The hash value is used to store the key in the hash table, as an index.
- The hash function can return the same hash value for two or more keys.
- When two or more keys are given the same hash value, it is called a collision. To handle this collision, we use collision resolution techniques.
Collision resolution techniques
There are two types of collision resolution techniques.
- Separate chaining (open hashing)
- Open addressing (closed hashing)
Separate chaining
In this technique, a linked list is created from the slot in which collision has occurred, after which the new key is inserted into the linked list. This linked list of slots looks like a chain, so it is called separate chaining. It is used more when we do not know how many keys to insert or delete.
Time complexity
- Its worst-case complexity for searching is o(n).
- Its worst-case complexity for deletion is o(n).
Advantages of separate chaining
- It is easy to implement.
- The hash table never feels full, so we can add more elements to the chain.
- It is less sensitive to the function of hashing.
Disadvantages of separate chaining
- In this, cache performance of chaining is not good.
- The memory wastage is too much in this method.
- It requires more space for element links.
Open addressing
Open addressing is a collision-resolution method that is used to control the collision in the hashing table. There is no key stored outside of the hash table. Therefore, the size of the hash table is always greater than or equal to the number of keys. It is also called closed hashing.
The following techniques are used in open addressing:
- Linear probing
- Quadratic probing
- Double hashing
Linear probing
In this, when the collision occurs, we perform a linear probe for the next slot, and this probing is performed until an empty slot is found. In linear probing, the worst time to search for an element is O(table size). The linear probing gives the best performance of the cache but its problem is clustering. The main advantage of this technique is that it can be easily calculated.
Disadvantages of linear probing
- The main problem is clustering.
- It takes too much time to find an empty slot.
Quadratic probing
In this, when the collision occurs, we probe for i2th slot in ith iteration, and this probing is performed until an empty slot is found. The cache performance in quadratic probing is lower than the linear probing. Quadratic probing also reduces the problem of clustering.
Double hashing
In this, you use another hash function, and probe for (i * hash 2(x)) in the ith iteration. It takes longer to determine two hash functions. The double probing gives the very poor cache performance, but there is no clustering problem in it.
Hashing with Chaining in Data Structure
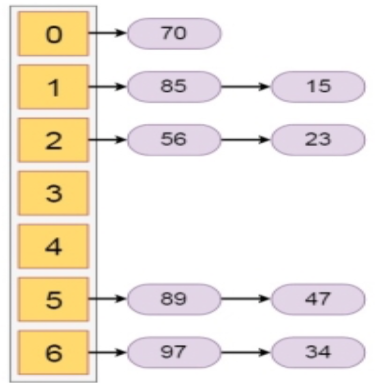
In this section we will see what is hashing with chaining. Chaining is one collision resolution technique. We cannot avoid collision, but we can try to reduce the collision, and try to store multiple elements for the same hash value.
This technique assumes that our hash function h(x) ranges from 0 to 6. So for more than 7 elements, there must be some elements that will be placed inside the same room. For that we will create a list to store them accordingly. In each time we will add at the beginning of the list to perform insertion in O(1) time
Let us see the following example to get a better idea. If we have some elements like {15, 47, 23, 34, 85, 97, 65, 89, 70}. And our hash function is h(x) = x mod 7.
The hash values will be
X | h(x)=x mod 7 |
15 | 1 |
47 | 5 |
23 | 2 |
34 | 6 |
85 | 1 |
97 | 6 |
56 | 2 |
89 | 5 |
70 | 0 |
The Hashing with chaining will be like −
Key takeaway
- Hashing is the process of mapping a large amount of data item to a smaller table with the help of hashing function.
- Hashing is also known as the Hashing Algorithm or Message Digest Function.
- A fixed process converts a key to a hash key is known as a Hash Function.
- Hash table or hash map is a data structure used to store key-value pairs.
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
● When only a few elements are in the list.
● When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pas. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
Compare and swap adjacent elements of the list if they are out of order. After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Algorithm
BubbleSort(A[0..n - 1])
//The algorithm sorts array A[0..n - 1] by bubble sort
//Input: An array A[0..n - 1] of orderable elements
//Output: Array A[0..n - 1] sorted in ascending order
For i=0 to n - 2 do
For j=0 to n - 2 - i do
If A[j + 1]<A[j ]
Swap A[j ] and A[j + 1
Example :
89 ↔️ 45 68 90 29 34 17
45 89 ↔️ 68 90 29 34 17
45 68 89 ↔️ 90 ↔️ 29 34 17
45 68 89 29 90 ↔️ 34 17
45 68 89 29 34 90 ↔️ 17
45 68 89 29 34 17 |90
45 ↔️ 68 ↔️ 89 ↔️ 29 34 17 |90
45 68 29 89 ↔️ 34 17 |90
45 68 29 34 89 ↔️ 17 |90
45 68 29 34 17 |89 90
Explanation: The first 2 bubble style passes are mentioned as 89, 45, 68, 90, 29, 34, 17. After a swap of two elements is completed, a new line is seen. The elements to the right of the vertical bar are in their final position and are not taken into account in the algorithm's subsequent iterations.
Performance analysis of bubble sort algorithm:
Clearly, there are n times of the outer loop. In this analysis, the only difficulty is in the inner loop. If we think of a single time the inner loop loops, by remembering that it can never loop more than n times, we can get a clear bound. Since the outer loop can complete n times with the inner loop, the comparison should not take place more than O(n2) times.
For all arrays of size n, the number of key comparisons for the bubble sort version given above is the same.
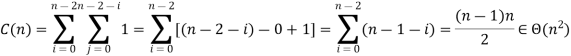
It depends on the feedback for the number of key swaps. It's the same as the number of primary comparisons, for the worst case of declining arrays.
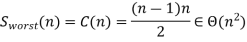
Observation: If no trades are made by going through the list, the list is sorted and we can stop the algorithm.
While the new version runs on certain inputs faster, in the worst and average situations, it is still in O(n2). The type of bubble is not very useful for a large input set. How easy it is to code the type of bubble.
Basic Message from Brute Force Method
A first use of the brute-force method often results in an algorithm that can be strengthened with a small amount of effort. Compare successive elements of a given list with a given search key until either a match is found (successful search) or the list is exhausted without finding a match (unsuccessful search).
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT - 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaway
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Merge Sort
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1 : Divide the list into sublists such that each sublist contains only one element.
Step 2 : Sort each sublist and Merge them.
Step 3 : Repeat Step 2 till the entire list is sorted.
Example : Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1 : A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
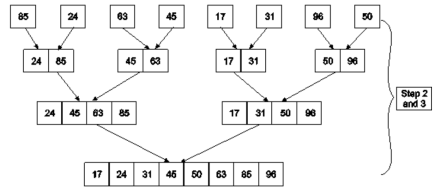
Fig. 4: Example
Step 2 : Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3 : Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example : Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1 :
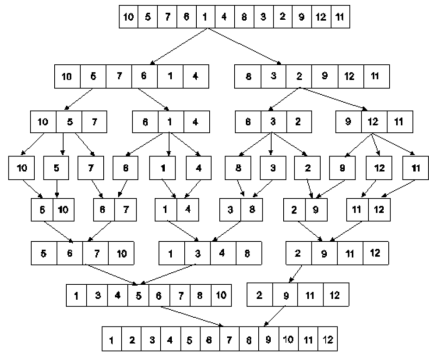
Fig 5: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA : = 1,
LB : = 1 and
LC : = 1.
At each step , we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A .
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Key takeaway
- Merge Sort is based on a divide and conquer strategy.
- It divides the unsorted list into n sublists such that each sublist contains one element.
- Each sublist is then sorted and merged until there is only one sublist.
Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime. Heap sort requires the creation of a Heap data structure from the specified array and then the use of the Heap to sort the array.
You should be wondering how it can help to sort the array by converting an array of numbers into a heap data structure. To understand this, let's begin by knowing what a heap is.
Heap is a unique tree-based data structure that meets the following special heap characteristics:
- Shape property : The structure of Heap data is always a Complete Binary Tree, which means that all tree levels are fully filled.
2. Heap property : Every node is either greater or equal to, or less than, or equal to, each of its children. If the parent nodes are larger than their child nodes, the heap is called Max-Heap, and the heap is called Min-Heap if the parent nodes are smaller than their child nodes.
The Heap sorting algorithm is split into two basic components:
● Creating an unsorted list/array heap.
● By repeatedly removing the largest/smallest element from the heap, and inserting it into the array, a sorted array is then created.
Complexity analysis of heap sort
Time complexity :
● Worst case : O(n*log n)
● Best case : O(n*log n)
● Average case : O(n*log n)
Space complexity : O(1)
Key takeaway :
- Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime.
- Heap sorting is very fast and for sorting it is widely used.
- Heap sorting is not a stable type, and requires constant space to sort a list.
Radix Sort
Radix sort sorts the elements in the same way that the students' names are sorted alphabetically. Because there are 26 alphabets in English, there are 26 radix in that situation. The names are classified in the first pass according to the ascending order of the first letter of the names.
The names are classified in the second pass according to the ascending order of the second letter. The same procedure is repeated until the sorted list of names is discovered. The names generated in each run are stored in the bucket. The number of passes is determined by the maximum letter length of the name.
When it comes to integers, radix sort arranges the numbers by their digits. From LSB to MSB, the comparisons are done between the digits of the number. The number of passes is determined by the number of digits in the longest number.
Example
Consider the array below, which has a length of 6. Radix sort is used to sort the array.
A = {10, 2, 901, 803, 1024}
Pass 1: (Sort the list according to the digits at 0's place)
10, 901, 2, 803, 1024.
Pass 2: (Sort the list according to the digits at 10's place)
02, 10, 901, 803, 1024
Pass 3: (Sort the list according to the digits at 100's place)
02, 10, 1024, 803, 901.
Pass 4: (Sort the list according to the digits at 1000's place)
02, 10, 803, 901, 1024
As a result, the sorted list obtained in step 4 is ordered using radix sort.
Algorithm
● Step 1:Find the largest number in ARR as LARGE
● Step 2: [INITIALIZE] SET NOP = Number of digits
in LARGE
● Step 3: SET PASS =0
● Step 4: Repeat Step 5 while PASS <= NOP-1
● Step 5: SET I = 0 and INITIALIZE buckets
● Step 6:Repeat Steps 7 to 9 while I
● Step 7: SET DIGIT = digit at PASSth place in A[I]
● Step 8: Add A[I] to the bucket numbered DIGIT
● Step 9: INCREMENT bucket count for bucket
numbered DIGIT
[END OF LOOP]
● Step 10: Collect the numbers in the bucket
[END OF LOOP]
● Step 11: END
Time complexity
Best case : Ω(n+k)
Average case : θ(nk)
Worst case : O(nk)
Space complexity : O(n+k) ( worst case)
Key takeaway
- Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime.
- Heap sort requires the creation of a Heap data structure from the specified array and then the use of the Heap to sort the array.
- Radix sort sorts the elements in the same way that the students' names are sorted alphabetically.
References:
1. Aaron M. Tenenbaum, Yedidyah Langsam and Moshe J. Augenstein, “Data Structures Using C and C++”, PHI Learning Private Limited, Delhi India
2. Horowitz and Sahani, “Fundamentals of Data Structures”, Galgotia Publications Pvt Ltd Delhi India.
3. Lipschutz, “Data Structures” Schaum’s Outline Series, Tata McGraw-hill Education (India) Pvt. Ltd.
4. Thareja, “Data Structure Using C” Oxford Higher Education.
5. AK Sharma, “Data Structure Using C”, Pearson Education India.