Unit-1
Error and roots of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Computers-
“The computer is an electronic device capable of accepting information, applying prescribed processes to the information, and supplying the results of these processes.”
Algorithm-
It is a step-by-step procedure made up of mathematical and/or logical operations designed to solve a particular problem.
Flow-chart-
Flow chart is a pictorial representation of a specific sequence of steps to be used by a computer.
The commonly used symbols in a flow chart-
1.Terminal point
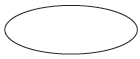
2. Input / Output-

3. Decision logic-
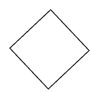
4. Processing operation box-

5. Connector point-
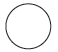
Mathematical preliminaries-
Continuity of a function-
Continuity- suppose that a function f(x) is defined in the interval I, then it is said to be continuous at x=a , if
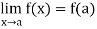
Differentiability- A function f(x) is said to be differentiable at x = a if
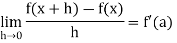
exists where ‘a’ belongs to I
Rolle’s theorem-
Let f(x) be a continuous function on the bounded interval [a, b] and differentiable on (a, b). If f(a) = f(b) then-
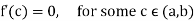
Mean value theorem for derivatives-
Suppose that f(x) be a function of x such that,
1. if it is continuous in [a, b]
2. if it is differentiable in (a, b)
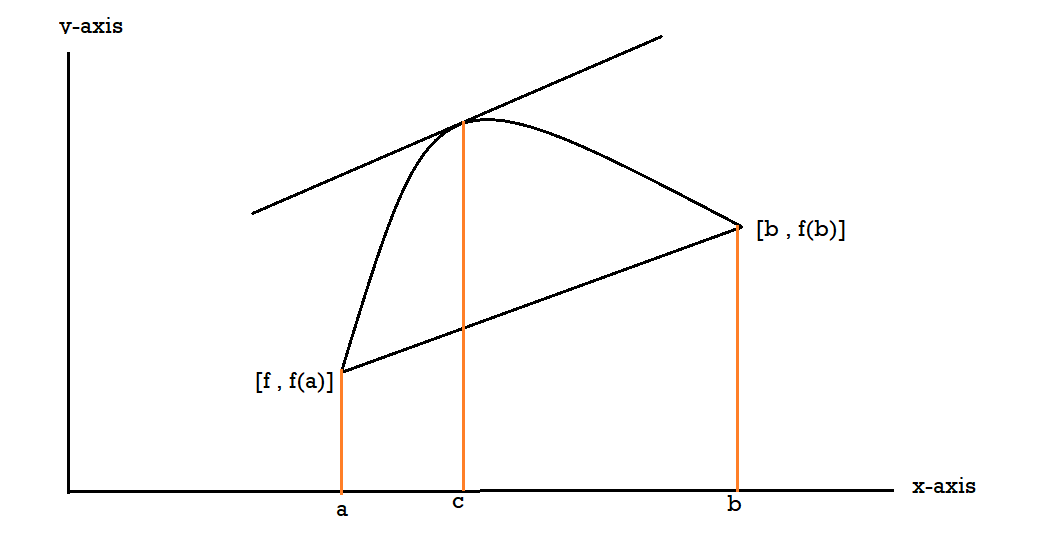
Then there at least exists a value cϵ (a, b)
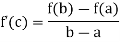
Proof:
Let’s define a function g(x),
g(x) = f(x) – Ax …………(1)
Here A is a constant which is to be determined,
So that,
g(a) = g(b)
now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
so,
g(a) = g(b),
f(a) – Aa = f(b) – Ab,
which gives,
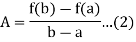
As right hand side of eq. (1) is continuous in [a, b], so that g(x) is continuous.
And right hand side of eq. (1) is differential in (a, b), so that g(x) is differentiable in (a, b).
And g(a) = g(b), because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
here we know that, x = c,
g’(c) = f’(c) – A
as g’(c) = 0, then
f’(c) – A =0
so that,
f’(c) = A,
from equation (2), we get
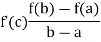
Hence proved
Example: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1) (x-2) (x-3)
f(x) = x-6x²+11x-6
now at x = 0, we get
f(0) = -6 and
at x = 4, we get.
f(4) = 6
diff. the function w. r. t. x, we get
f’(x) = 3x²-6x+11
suppose x = c, we get
f’(c) = 3c²-6c+11
by Lagrange’s mean value theorem,
f’(c) = 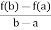 =
= 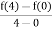 =
= 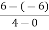 = 3
= 3
now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 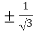
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Taylor’s formula-
Taylor’s theorem for a function f(x) can be expressed as an infinite series as follows-
f(x) = f(a) + (x – a) f’(a) + 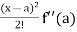 + ………
+ ……… .
.
Example: Expand the function 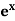 in ascending powers of (x – 1) by using Taylor’s theorem.
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a) f’(a) + 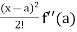 + ………
+ ……… . ……(1)
. ……(1)
Here f(x) = 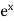 and a = 1
and a = 1
Now,
f’(x) = 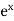 and f’(a) = e
and f’(a) = e
f’’(x) = 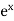 and f’’(a) = e
and f’’(a) = e
put these values in equation (1),
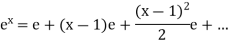
Take ‘e’ as common,
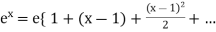
Which is the required expansion.
Key takeaways-
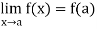
3. Taylor’s formula-
4. f(x) = f(a) + (x – a)f’(a) + 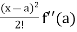 + ………
+ ……… .
.
The numerical method provides much wider range to solve the problem that are not possible by analytical methods. There are two ways to solve the numerical methods
a) Exact method: This provides the exact solution of the problem so there will be no error in this.
b) Trial and error or iteration or Approximation method: This will provide the approximate solution that contains certain amount of error which can be tolerated.
Types of Error:
The Approximate error is the numerical difference between the quantity of exact solution and the approximate value of the solution.
Let X be the exact solution and the approximate value of the solution is denoted by 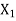 , then the absolute error is defined as
, then the absolute error is defined as
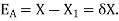
2. Relative Error:
The error obtained by dividing the approximate solution to the exact solution is known as relative error and is denoted by 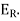
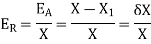
The percentage error is the 100 times of the relative error i.e.
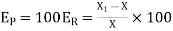 .
.
The absolute accuracy is magnitude absolute error.
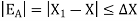 .
.
The relative accuracy is the magnitude of the relative error.
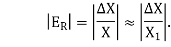
3. Algorithmic Error:
A error caused due to rounding off the number or truncation is called algorithmic error.
4. Truncation Error:
The truncation errors are caused by approximated values or on replacing the infinite process to a finite value.
Example: 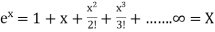 is replaced by
is replaced by  .
.
Then truncation error is 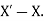
5. Round off Error:
The digit that are used to express a number are called significant digits or significant figures.eg 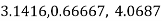 etc.
etc.
In numerical computation, the large number of digits cutting the usual figure is called rounding off. The rule to rounding off is
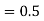
The number thus rounded-off is said to be correct to n significant figures.
The round off error can be reduced by carrying out the computation to more significant figures at each step of the computation.
Example: Numbers –Round off
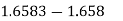 here 0.0003< 0.0005 unchanged
here 0.0003< 0.0005 unchanged
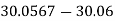 here 0.006>0.005 so, 5=5+1
here 0.006>0.005 so, 5=5+1
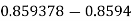 here 0.00007>0.00005 so, 8=8+1
here 0.00007>0.00005 so, 8=8+1
6. Error Propagation:
The error propagation is carried out in the number of steps to get the solution.
The approximate value of the two numbers X and Y is X’ and Y’
Then absolute error is
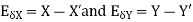
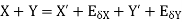
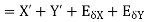
2. Absolute error in subtraction operation
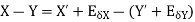
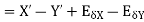
3. Absolute error in multiplication operation
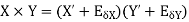
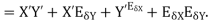
4. Absolute error in division operation
The absolute error 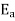 in the quotient of two numbers X and Y
in the quotient of two numbers X and Y
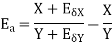
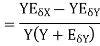
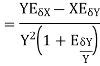
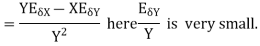
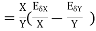 .
.
Example1: An approximate value of 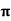 is given by
is given by 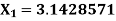 and its exact value is
and its exact value is 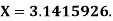 Find the absolute and relative errors.
Find the absolute and relative errors.
The absolute error is 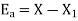
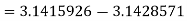
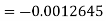 .
.
The relative error is
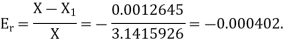
Example2: Find the difference 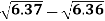 to three significant figure?
to three significant figure?
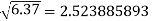
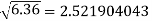
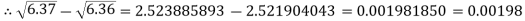
Correct to three decimal places.
Example3: Round –off the following number to two decimal places
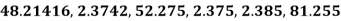
Number | Compare | changes | Rounded-off number |
48.21416 | 0.004<0.005 | No change | 48.21 |
2.3 742 | 0.004<0.005 | No change | 2.37 |
52.275 | 0.005=0.005 | 0.07+0.01=0.08 | 52.28 |
2.375 | 0.005=0.005 | 0.07+0.01=0.08 | 2.38 |
2.385 | 0.005=0.005 | 0.08+0.01=0.09 | 2.39 |
81.255 | 0.005=0.005 | 0.05+0.01=0.06 | 81.26 |
Example4: Find the absolute error if the number 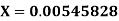 is truncate to three decimal places?
is truncate to three decimal places?
The given number is 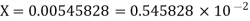
After truncate it to three decimal places the rounded value is 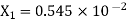
Therefore, the absolute error is 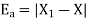
= 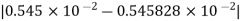
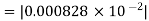
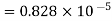 .
.
Generalized error formula (Derivation and Numerical)
Let-
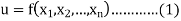
Be the function of 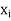 and let the error in each
and let the error in each 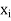 be
be 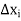 .
.
The error in u is given by-
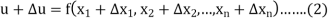
By using Taylor’s theorem, we expand RHS-
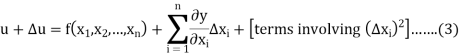
Let’s assume that the errors in  are small, so that the higher powers of
are small, so that the higher powers of  can be neglected,
can be neglected,
The above relation yields-
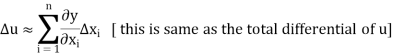
The formula for the relative error follows-
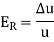
Key takeaways-
The Approximate error is the numerical difference between the quantity of exact solution and the approximate value of the solution.
2. Truncation Error:
The truncation errors are caused by approximated values or on replacing the infinite process to a finite value.
3. Algorithmic Error: A error caused due to rounding off the number or truncation is called algorithmic error.
4. Error Propagation:
The error propagation is carried out in the number of steps to get the solution.
The approximate value of the two numbers X and Y is X’ and Y’
Then absolute error is
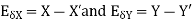
Concept of roots of an equation-
There are two types of equations Linear and Nonlinear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand nonlinear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 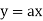 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
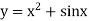 is a non-linear equation.
is a non-linear equation.
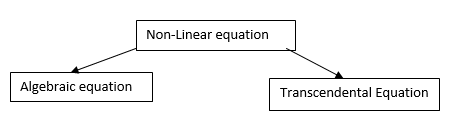
Algebraic Equation: If f(x) is a pure polynomial, then the equation 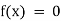 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 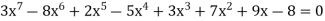
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 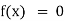 is called transcendental equation.
is called transcendental equation.
Ex 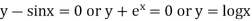
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Bisection method:
This method is consists of finding the root of the equation 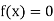 which lies between a and b (say).
which lies between a and b (say).
The function 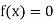 is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
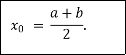
If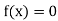 , then t
, then t
the correct root is 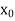 .But if
.But if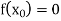 , then the root either lies between a and
, then the root either lies between a and 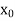 or
or 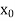 and b according as
and b according as 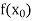 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
Note: Remember that root of an equation lies between its positive and negative values and we take average of them to come closer to its accurate root.
Example1 Find a real root of 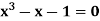 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
Let 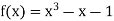 then by hit and trial we have
then by hit and trial we have
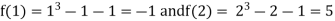
Thus 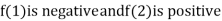 .So the root of the given equation should lie between 1 and 2.
.So the root of the given equation should lie between 1 and 2.

Now, 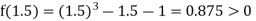
i.e., positive so the root of the given equation must lie between 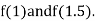

Now, 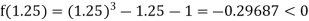
i.e., negative so the root of the given equation lies between 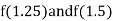
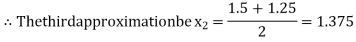
Now, 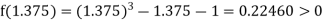
i.e., positive so the root of the given equation lies between 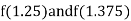
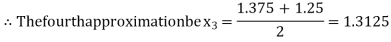
Now, 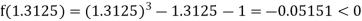
i.e., negative so that the root of the given equation lies between 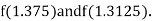
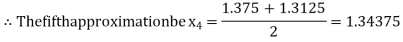
Now, 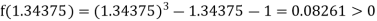
i.e., positive so that the root of the given equation lies between 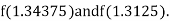
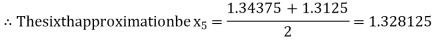
Now, 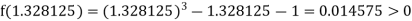
i.e., positive so that the root of the given equation lies between 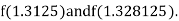
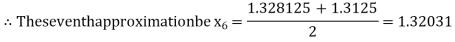
Now, 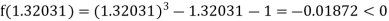
i.e., negative so that the root of the given equation lies between 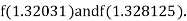
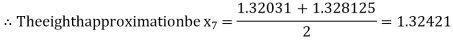
Now, 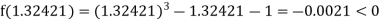
i.e., negative so that the root of the given equation lies between 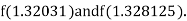
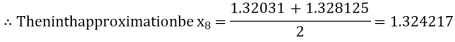
Hence the approximate root of the given equation is 1.32421
Example2 Find the root of the equation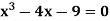 , using the bisection method.
, using the bisection method.
Let 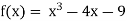 then by hit and trial we have
then by hit and trial we have
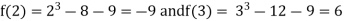
Thus 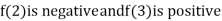 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 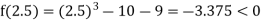
i.e., negative so the root of the given equation must lies between 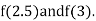

Now, 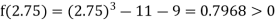
i.e., positive so the root of the given equation must lie between 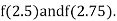
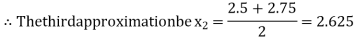
Now, 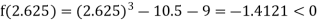
i.e., negative so the root of the given equation must lie between 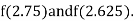
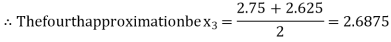
Now, 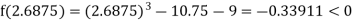
i.e., negative so the root of the given equation must lie between 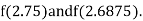
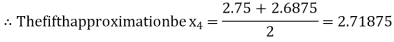
Now, 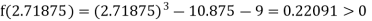
i.e., positive so the root of the given equation must lie between 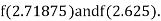
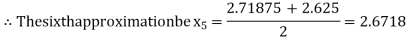
Now, 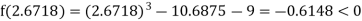
i.e., negative so the root of the given equation must lie between 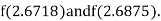
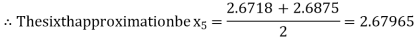
Hence the root of the given equation correct to two decimal place is 2.67965.
Example3 Find the root of the equation 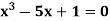 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
Let 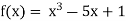
Where 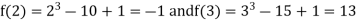
Thus 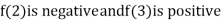 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 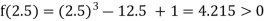
i.e., positive so the root of the given equation must lie between 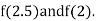

Now, 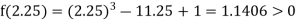
i.e., positive so the root of the given equation must lie between 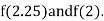

Now, 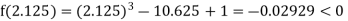
i.e., negative so the root of the given equation must lie between 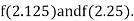
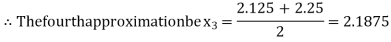
Now, 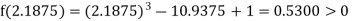
i.e., positive so the root of the given equation must lie between 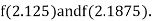
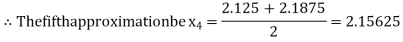
Now, 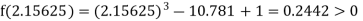
i.e., positive so the root of the given equation must lie between 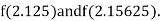
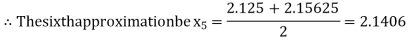
Now, 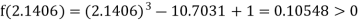
i.e., positive so the root of the given equation must lie between 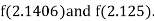
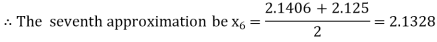
Now, 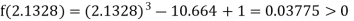
i.e., positive so the root of the given equation must lie between 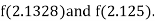
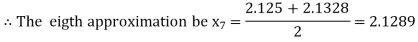
Now, 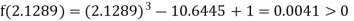
i.e., positive so the root of the given equation must lie between 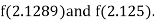
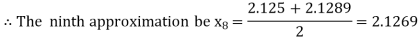
Hence the root of the given equation correct to two decimal place is 2.1269
Write the computer program to implement bisection method-
Iteration method-
To find the roots of equation f(x) = 0 by successive approximations,
We will write it as-
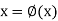
Now let 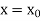 be an initial approx. of the root(desired)
be an initial approx. of the root(desired) 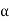 , then the first approx. is given as-
, then the first approx. is given as-
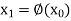
The second approximation is-
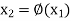
Same as the n’th approximation is given as-
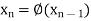
Computer program for iteration method-
Example: Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
Here we have-
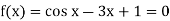
Now,
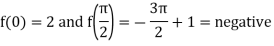
A root lies between 0 and  .
.
We can rewrite the equation as-
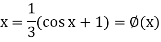
We have-
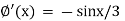
And
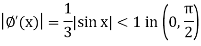
Here we can apply iteration method, starting with
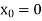
Then the successive approximation is-
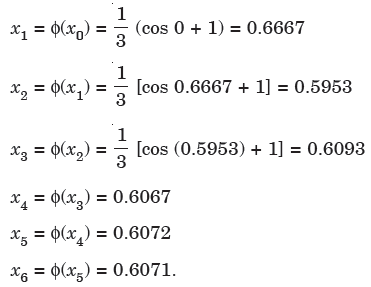
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Example: Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
Here
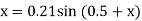
First approximation of x is gives as-
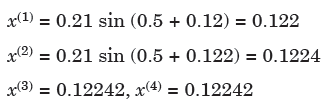
Here last two approx. are same, hence required root is 0.12242.
Regula - Falsi Method (Method of false position)
This is the oldest method of finding the approximate numerical value of a real root of an equation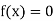 .
.
In this method we suppose that 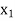 and
and 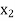 are two points where
are two points where 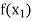 and
and 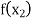 are of opposite sign. Let
are of opposite sign. Let 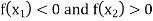
Hence the root of the equation 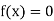 lies between
lies between 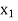 and
and 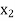 and so,
and so, 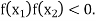
The Regula Falsi formula
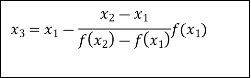
Find 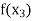 is positive or negative. If
is positive or negative. If 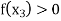 then root lies between
then root lies between 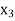 and
and 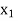 or if
or if 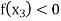 then root lies between
then root lies between 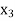 and
and 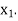 similarly we calculate
similarly we calculate 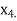
Proceed in this manner until the desired accurate root is found.
Example1 Find a real root of the equation 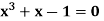 near
near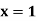 , correct to three decimal places by the Regula Falsi method.
, correct to three decimal places by the Regula Falsi method.
Let 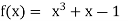
Now, 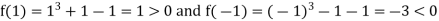
And also 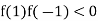
Hence the root of the equation 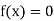 lies between
lies between 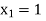 and
and 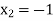 and so,
and so, 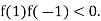
By Regula Falsi Method
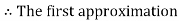
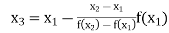
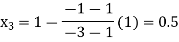
Now, 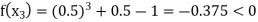
So, the root of the equation 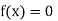 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 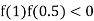
By Regula Fasli Method
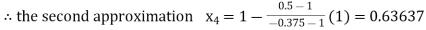
Now, 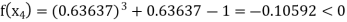
So, the root of the equation 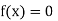 lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 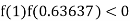
By Regula Fasli Method
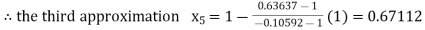
Now, 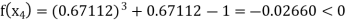
So, the root of the equation 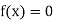 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 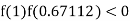
By Regula Fasli Method
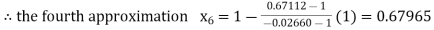
Now, 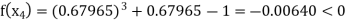
So, the root of the equation 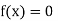 lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 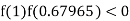
By Regula Fasli Method
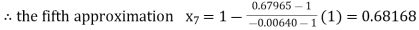
Now, 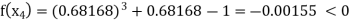
So, the root of the equation 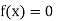 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 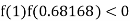
By Regula Fasli Method
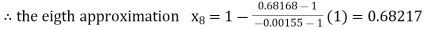
Now, 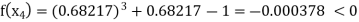
Hence the approximate root of the given equation near to 1 is 0.68217
Example2 Find the real root of the equation
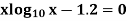
By the method of false position correct to four decimal places
Let 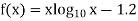
By hit and trail method
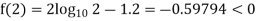
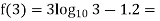 0.23136 > 0
0.23136 > 0
So, the root of the equation 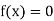 lies between
lies between 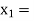 2 and
2 and 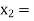 3 and also
3 and also 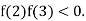
By Regula Falsi Method
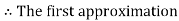
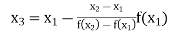
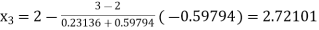
Now, 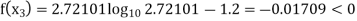
So, root of the equation 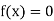 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 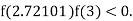
By Regula Falsi Method
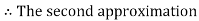
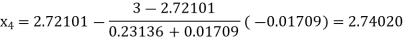
Now, 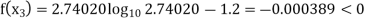
So, root of the equation 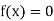 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 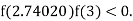
By Regula Falsi Method
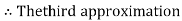
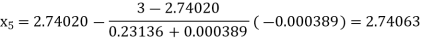
Now, 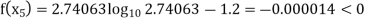
So, root of the equation 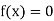 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 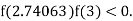
By Regula Falsi Method
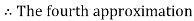
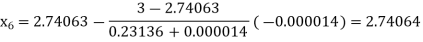
Hence the root of the given equation correct to four decimal places is 2.7406
Example3 Apply Regula Falsi Method to solve the equation
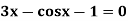
Let 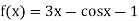
By hit and trail
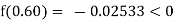
And 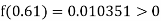
So, the root of the equation lies between 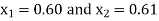 and also
and also 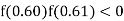
By Regula Falsi Method
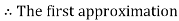
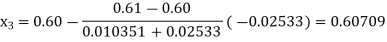
Now, 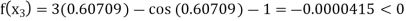
So, root of the equation 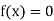 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 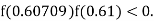
By Regula Falsi Method
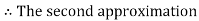

Now, 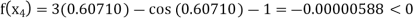
So, root of the equation 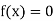 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 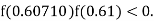
By Regula Falsi Method


Hence the root of the given equation correct to five decimal place is 0.60710.
Key takeaways-
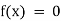
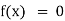
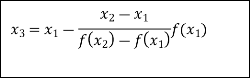
Newton-Raphson Method:
Let 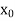 be the approximate root of the equation
be the approximate root of the equation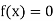 .
.
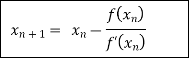 By Newton Raphson formula
By Newton Raphson formula 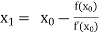
In general,
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: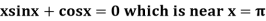 .
.
Given 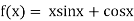
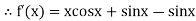
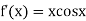
By Newton Raphson Method
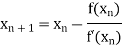
= 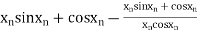
=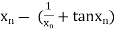
The initial approximation is 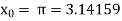 in radian.
in radian.
For n =0, the first approximation 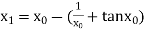
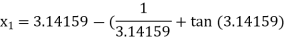
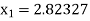
For n =1, the second approximation 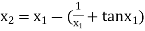
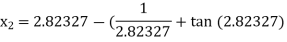
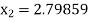
For n =2, the third approximation 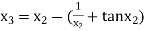
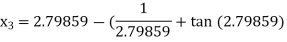
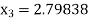
For n =3, the fourth approximation 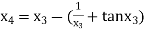
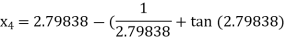
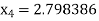
Hence the root of the given equation corrects to five decimal place 2.79838.
Example2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 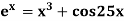 near to 4.5
near to 4.5
Let
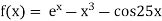
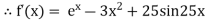
The initial approximation 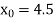
By Newton Raphson Method
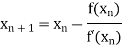
For n =0, the first approximation 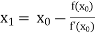
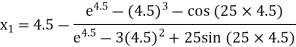
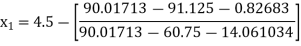
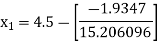
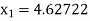
For n =1, the second approximation 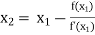
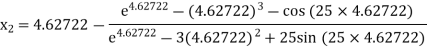
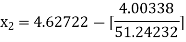
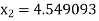
For n =2, the third approximation 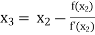
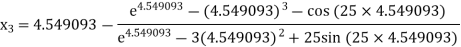
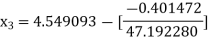
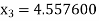
For n =3, the fourth approximation 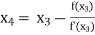
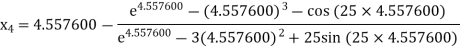
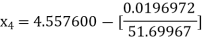
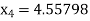
Hence the root of the equation correct to three decimal places is 4.5579
Example3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 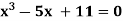
Let 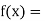
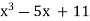
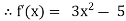
By Newton Raphson Method
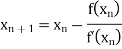
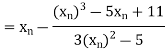
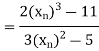
Let the initial approximation be 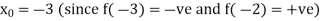
For n=0, the first approximation 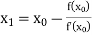
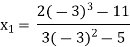
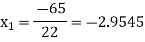
For n=1, the second approximation 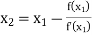
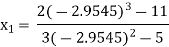
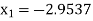
For n=2, the third approximation 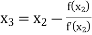
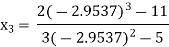
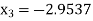
Since 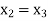 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
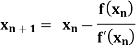
Muller’s method is generalization of secant method. Muller method starts with three initial approximations to the root and then join them with a second-degree polynomial. then the formula is used to find out the roots of quadratic for the next approximation.
Let 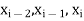 be the three distinct approximations to a root f(x) = 0 and let
be the three distinct approximations to a root f(x) = 0 and let 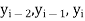 be the corresponding values of y = f(x).
be the corresponding values of y = f(x).
Let us assume P(x) = 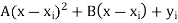 be the parabolic which is passing through the points (
be the parabolic which is passing through the points (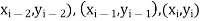 , we have-
, we have-
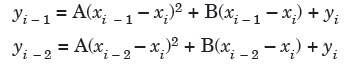
From the above two equations, we get-
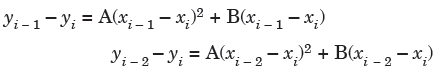
Solution of the above two equations is given as-
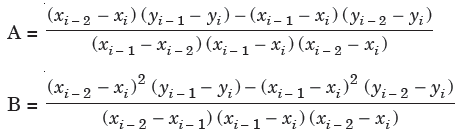
With the values of A and B, the quadratic equation now gives next approximation-
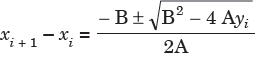
The solution from above equation leads to inaccurate results, so that this is written as-
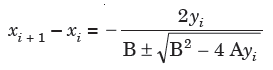
Program for Muller’s method-
Example: Find the root of the equation 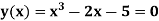 which lies between 2 and 3
which lies between 2 and 3
Sol.
Here let 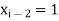 ,
, 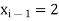 and
and 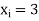 . Then
. Then 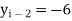
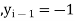 and
and 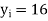
Hence
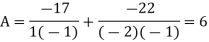
And
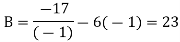
The quadratic equation is given by-
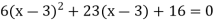
It gives the next approximation-
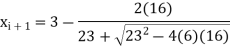
The positive sign is chosen as B is +ve,
Hence
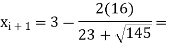
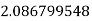
The error is calculated as-
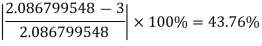
Here the error is large, so we do the next iteration-
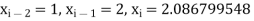
And
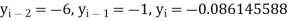
Now using these values, we get-
A = 5.086799558 and B = 10.96986336
The next approximation is-

The error is 0.373553519%.
Convergence-
A sequence of iterates 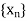 is said to converge with order
is said to converge with order 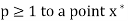 if
if
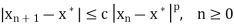
For some constant c > 0.
Note-
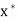
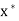
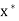
Order and Rate of Convergence
Let 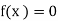 be the given equation. Let α be its exact root.
be the given equation. Let α be its exact root.
Then 
Then the positive number p is said to be order of convergence if,
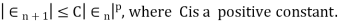
If p=1, then convergence is linear and if p=2 , then it is quadratic.
a) Bisection Method: The percentage error 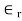 defined by
defined by
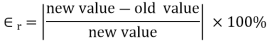
The rate of convergence for bisection method is 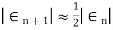
i.e. it converges linearly.
b) Regula-Falsi Method: The rate of convergence is
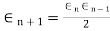
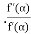
Here p=1.618 and is linear.
c)Newton Raphson Method: The rate of convergence is
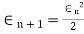
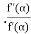
Here p=2 so the convergence is quadratic
d) Secant Method: The rate of convergence is
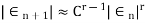
Order of convergence is non integer and is greater than one , so is super linear.
Note: Order of Convergence
1) Bisection Method: p=1 (linear)
2) Regula-Falsi Method: 1 < p < 2 (super linear).
3) Newton Raphson Method: p = 2 (quadratic).
4) Secant Method: p=1.618 (super linear).
Roots of Polynomial Equations using Birge-Vieta method-
This method is the modified form of Newton-Raphson method.
Let us consider a polynomial equation of degree ‘n’-
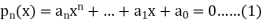
Suppose 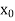 be an initial approximation to the root of
be an initial approximation to the root of 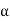 .
.
The Newton-Raphson iteration formula for improving this approximation-
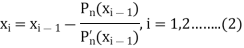
We shall be able to find both 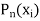 and
and 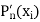 at any
at any 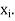
We will evaluate as-
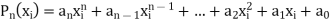
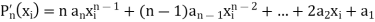
Because of the lot of computations involved and due to round off errors, this method is not efficient.
Let the us consider the evaluation of 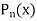 and
and 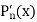 at
at 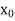 by using Horner’s method-
by using Horner’s method-
We have-
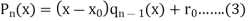
Where
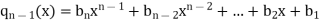
And
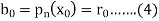
Now we shall find the derivative 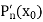 by using Horner’s method.
by using Horner’s method.
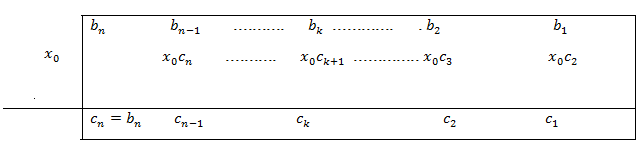
We divide 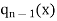 by
by 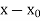 using Horner’s method,
using Horner’s method,
We write-
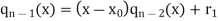
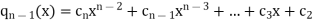
We get  as given in table-
as given in table-
We have-
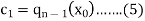
Now from equations (3) and (4), we have-
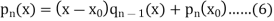
Now differentiate both sides of equation (6) w.r.t. x-
We get-
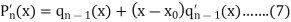
Putting 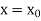 in equation (7), we get-
in equation (7), we get-
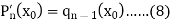
Comparing (5) and (8), we get-
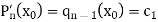
Hence the Newton-Raphson method implies to-
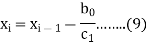
Example: Find all the roots of polynomial equation 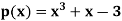 rounded off to three decimal places.
rounded off to three decimal places.
[Stop the iteration if |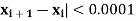
Sol.
The equation has three roots.
As there is only one change in the sign of the coefficient, by Descarts’ rule of sign the equation can have at most one positive real root.
The equation has no negative real roots since p(-x) = 0 has no change of sign of coefficients.
Here p(x) = 0 is of one degree, it has at least one real root.
So that the given equation has one positive real root and a complex pair.
Now let’s find the real roots by Birge-Vieta method-
The initial iteration is-
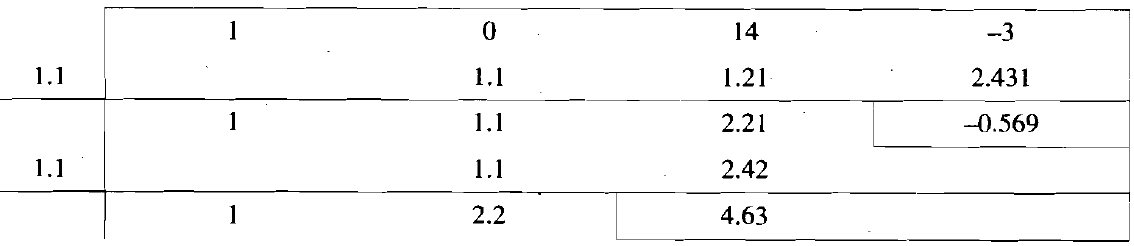
So that-
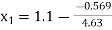 = 1.22289
= 1.22289
Similarly
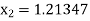
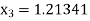
Here we see that 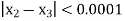 so that we stop the iteration.
so that we stop the iteration.
Hence the value of root is 1.213
Now we get the deflated polynomial of p(x).
In order to obtain deflated polynomial, we need to find the quadratic equation by using the final approximation. [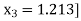

Here we notice p (1.213) = -0.0022,
That is, the magnitude of the error in satisfying p(x) = 0 is 0.0022.
We get-
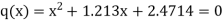
The roots of this quadratic equation are given by- [using quadratic equation]-
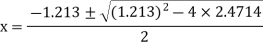
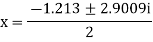
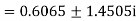
The three roots of the equation rounded off to three decimal places are 1.213, 0.6065+1.4505i and -0.6065 - 1.4505i
Key takeaways-
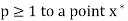
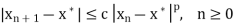
2. The rate of convergence for bisection method is 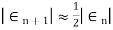
3. Regula-Falsi Method: The rate of convergence is 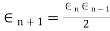
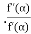
Here p=1.618 and is linear.
References