UNIT 1
INTRODUCTION – Well defined learning problems
For any learning system, we must be knowing the three elements — T (Task), P (Performance Measure), and E (Training Experience). At a high level, the process of the learning system looks as below.
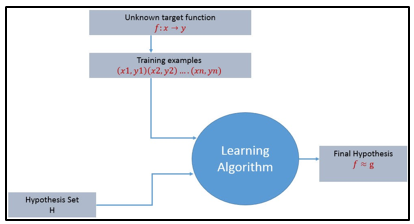
Figure.1 Learning process algorithm
The learning process starts with task T, performance measure P, and training experience E, and objective are to find an unknown target function. The target function is an exact knowledge to be learned from the training experience and its unknown. For example, in a case of credit approval, the learning system will have customer application records as experience and the task would be to classify whether the given customer application is eligible for a loan. So in this case, the training examples can be represented as (x1,y1)(x2,y2)..(xn,yn) where X represents customer application details and y represents the status of credit approval.
KEY TAKEAWAYS
The goal of the learning process is to design a learning system that follows the learning process, it requires considering a few design choices. The design choices are used to decide the key components:
1. Kind of training experience
2. The exact type of knowledge to be learned (it involves Choosing Target Function). At the initial stage, steps of target function are not known.
3. A detailed representation of target knowledge (Choosing a representation for the Target Function)
4. A learning mechanism (Choosing an approximation algorithm for the Target Function)
We will look into the checkers learning problem and apply the above design choices. For a checkers learning problem, the three elements will be,
1. Task T: To play checkers
2. Performance measure P: Total percent of the game won in the tournament.
3. Training experience E: A set of games played against itself
Training experience
During the design of the checker's learning system, the type of training experience available for a learning system will have a significant effect on the success or failure of the learning.
In the case of indirect training experience, the move sequences for a game and the final result (win, loss, or draw) are given for some games. How to assign credit or blame to individual moves is the credit assignment problem.
II. Teacher or Not — Supervised — The training experience will be labeled, which means, all the board states will be labeled with the correct move. So the learning takes place in the presence of a supervisor or a teacher.
Unsupervised — The training experience will be unlabelled, which means, all the board states will not have the moves. So the learner generates random games and plays against itself with no supervision or teacher involvement.
Semi-supervised — Learner generates game states and asks the teacher for help in finding the correct move if the board state is confusing.
III. Is the training experience good — Do the training examples represent the distribution of examples over which the final system performance will be measured.
Performance is best when training examples and test examples are from the same/a similar distribution.
The checker player learns by playing against oneself. Its experience is indirect. It may not encounter moves that are common in human expert play. Once the proper training experience is available, the next design step will be choosing the Target Function.
Choosing the Target Function
In this design step, we need to determine exactly what type of knowledge has to be learned and it's used by the performance program.
When you are playing the checkers game, at any moment, you decide on choosing the best move from different possibilities. You think and apply the learning that you have gained from the experience. Here the learning is, for a specific board, you move a checker such that your board state tends towards the winning situation. Now the same learning has to be defined in terms of the target function.
Here there are 2 considerations — direct and indirect experience.
During the direct experience, the checkers learning system, it needs only to learn how to choose the best move among some large search space. We need to find a target function that will help us choose the best move among alternatives. Let us call this function Choose Move and use the notation.
Choose Move: B →M to indicate that this function accepts as input any board from the set of legal board states B and produces as output some move from the set of legal moves M.
When there is an indirect experience, it becomes difficult to learn such a function. How about assigning a real score to the board state. So the function is V: B →R indicating that this accepts as input any board from the set of legal board states B and produces an output a real score. This function assigns the higher scores to better board states.
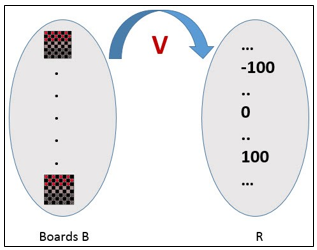
Figure 2
If the system can successfully learn such a target function V, then it can easily use it to select the best move from any board position.
Let us, therefore, define the target value V(b) for an arbitrary board state b in B, as follows:
1. if b is a final board state that is won, then V(b) = 100
2. if b is a final board state that is lost, then V(b) = -100
3. if b is a final board state that is drawn, then V(b) = 0
4. if b is not a final state in the game, then V (b) = V (b’), where b’ is the best final board state that can be achieved starting from b and playing optimally until the end of the game.
The (4) is a recursive definition and to determine the value of V(b) for a particular board state, it performs the search ahead for the optimal line of play, all the way to the end of the game. So this definition is not efficiently computable by our checkers playing program, we say that it is a non-operational definition.
The goal of learning, in this case, is to discover an operational description of V; that is, a description that can be used by the checkers-playing program to evaluate states and select moves within realistic time bounds.
It may be very difficult in general to learn such an operational form of V perfectly. We expect learning algorithms to acquire only some approximation to the target function ^V.
Choosing a representation for the Target Function
Now it's time to choose a representation that the learning program will use to describe the function ^V that it will learn. The representation of ^V can be as follows.
To keep the discussion simple, let us choose a simple representation for any given board state, the function ^V will be calculated as a linear combination of the following board features:
^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
Where w0 through w6 are numerical coefficients or weights to be obtained by a learning algorithm. Weights w1 to w6 will determine the relative importance of different board features.
Specification of the Machine Learning Problem at this time — Till now we worked on choosing the type of training experience, choosing the target function and its representation. The checkers learning task can be summarized as below.
Task T: Play Checkers
Performance Measure: % of games won in the world tournament
Training Experience E: opportunity to play against itself
Target Function: V: Board → R
Target Function Representation : ^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
The first three items above correspond to the specification of the learning task, whereas the final two items constitute design choices for the implementation of the learning program.
Choosing an approximation algorithm for the Target Function
Generating training data —
To train our learning program, we need a set of training data, each describing a specific board state b and the training value V_train (b) for b. Each training example is an ordered pair <b,V_train(b)>
For example, a training example may be <(x1 = 3, x2 = 0, x3 = 1, x4 = 0, x5 = 0, x6 = 0), +100">.
This is an example where black has won the game since x2 = 0 or red has no remaining pieces. However, such clean values of V_train (b) can be obtained only for board value b that are clear win, lose, or draw.
In the above case, assigning a training value V_train(b) for the specific boards b that are clean win, lose or draw is direct as they are direct training experience. But in the case of indirect training experience, assigning a training value V_train(b) for the intermediate boards is difficult. In such a case, the training values are updated using temporal difference learning. Temporal difference (TD) learning is a concept central to reinforcement learning, in which learning happens through the iterative correction of your estimated returns towards a more accurate target return.
Let Successor(b) denotes the next board state following b for which it is again the program’s turn to move. ^V is the learner’s current approximation to V. Using this information, assign the training value of V_train(b) for any intermediate board state b as below :
V_train(b) ← ^V(Successor(b))
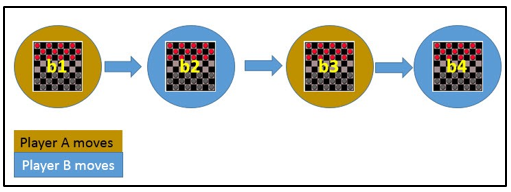
In the above figure, V_train(b1) ← ^V(b3), where b3 is the successor of b1. Once the game is played, the training data is generated. For each training example, the V_train(b) is computed.
Adjusting the weights
Now it's time to define the learning algorithm for choosing the weights and best fit the set of training examples. One common approach is to define the best hypothesis as that which minimizes the squared error E between the training values and the values predicted by the hypothesis ^V.
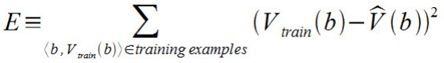
The learning algorithm should incrementally refine weights as more training examples become available and it needs to be robust to errors in training data
Least Mean Square (LMS) training rule is the one training algorithm that will adjust weights a small amount in the direction that reduces the error.
The LMS algorithm is defined as follows:

Final Design for Checkers Learning system
KEY TAKEAWAYS
Here there are 2 considerations — direct and indirect experience.
^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
Leave advanced mathematics to the experts. As you embark on a journey with ML, you’ll be drawn into the concepts that build the foundation of science, but you may still be on the other end of results that you won’t be able to achieve after learning everything. Fortunately, the experts have already taken care of the more complicated tasks and algorithmic and theoretical challenges. With this help, mastering all the foundational theories along with statistics of an ML project won’t be necessary.
Once you become an expert in ML, you become a data scientist. For those who are not data scientists, you don’t need to master everything about ML. All you have to do is to identify the issues which you will be solving and find the best model resources to help you solve those issues.
For example, for those dealing with basic predictive modeling, you wouldn’t need the expertise of a master in natural language processing. Why would you spend time being an expert in the field when you can just master the niches of ML to solve specific problems?
ML algorithms will always require much data when being trained. Often, these ML algorithms will be trained over a particular data set and then used to predict future data, a process that you can’t easily anticipate. The previously “accurate” model over a data set may no longer be as accurate as it once was when the set of data changes. For a system that changes slowly, the accuracy may still not be compromised; however, if the system changes rapidly, the ML algorithm will have a lesser accuracy rate given that the past data no longer applies.
ML algorithms can pinpoint the specific biases which can cause problems for a business. An example of this problem can occur when a car insurance company tries to predict which client has a high rate of getting into a car accident and tries to strip out the gender preference given that the law does not allow such discrimination. Even without gender as a part of the data set, the algorithm can still determine the gender through correlates and eventually use gender as a predictor form.
Developers always use ML to develop predictors. Such predictors include improving search results and product selections and anticipating the behavior of customers. One reason behind inaccurate predictions may be overfitting, which occurs when the ML algorithm adapts to the noise in its data instead of uncovering the basic signal.
ML algorithms running over fully automated systems have to be able to deal with missing data points. One popular approach to this issue is using the mean value as a replacement for the missing value. This application will provide reliable assumptions about data including the particular data missing at random.
Whether they’re being used in automated systems or not, ML algorithms automatically assume that the data is random and representative. However, having random data in a company is not common.
The best way to deal with this issue is to make sure that your data does not come with gaping holes and can deliver a substantial amount of assumptions.
Recommendation engines are already common today. While some may be reliable, others may not seem to be more accurate. ML algorithms impose what these recommendation engines learn. One example can be seen when a customer’s taste changes; the recommendations will already become useless. Experts call this phenomenon the “exploitation versus exploration” trade-off. In the event the algorithm tries to exploit what it learned devoid of exploration, it will reinforce the data that it has, will not try to entertain new data, and will become unusable.
To deal with this issue, marketers need to add the varying changes in tastes over time-sensitive niches such as fashion. With this step, you can avoid recommending winter coats to your clients during the summer.
KEY TAKEAWAYS
The Learning Task
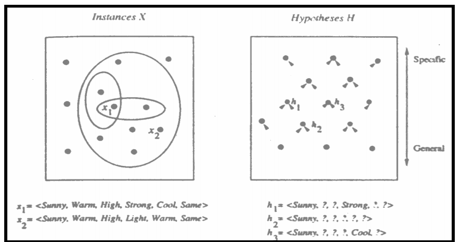
Given: Instances X: a set of items over which the concept is defined.
Hypotheses H: the conjunction of constraints on attributes.
Target concept c: c : X → {0, 1}
Training examples (positive/negative): <x,c(x)>
Training set D: available training examples
Determine: i A hypothesis h in H such that h(x) = c(x), for all x in X
More_general_than_or_equal_to relation
hj ≥ g hk ⇔ (∀x∈X)[(hk(x) =1)→(hj(x) =1)]
(Strictly) more_general_than relation
<Sunny,?,?,?,?,?> >g <Sunny,?,?,Strong,?,?>
More_General_Than Relation
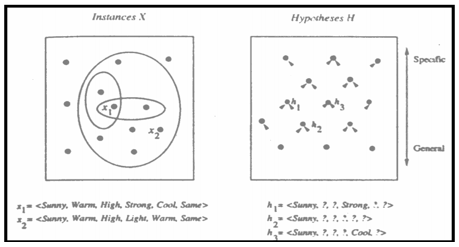
1. Initialize h to the most specific hypothesis in H
2. For each positive training example x For each attribute constraint ai in h If the constraint ai is satisfied by x Then do nothing Else replace ai in h by the next more general constraint satisfied by x
3. Output hypothesis h
Hypothesis Space Search by Find-S
Properties of Find-S Ignores every negative example (no revision to h required in response to negative examples). Why? What’re the assumptions for this? Guaranteed to output the most specific hypothesis consistent with the positive training examples (for conjunctive hypothesis space). Final h also consistent with negative examples provided the target c is in H and no error in D
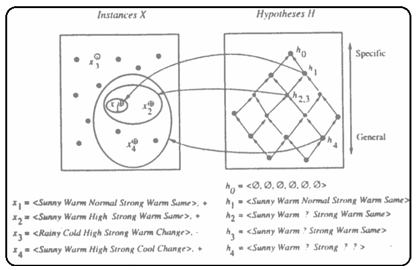
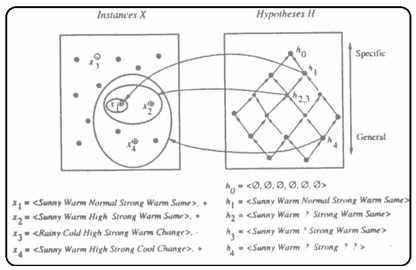
The List-Then-Eliminate algorithm initializes the version space to contain all hypotheses in H, then eliminates the inconsistent hypotheses, from training examples. The version space of hypotheses thus shrinks as more examples are observed until one hypothesis remains that is consistent with all the observed examples.
Presumably, this hypothesis is the desired target concept. If the data available is insufficient, to narrow the version space to a single hypothesis, then the algorithm can output the entire set of hypotheses consistent with the observed data.
The List-Then-Eliminate algorithm can be applied whenever the hypothesis space “H” is finite.
It has many advantages, including the fact that it is guaranteed to output all hypotheses consistent with the training data.
It requires exhaustively enumerating all hypotheses in H — an unrealistic requirement for all but the most trivial hypothesis spaces.
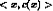
remove from
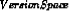
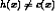
Candidate-Elimination Algorithm part 2
If d is a negative example
Remove from S any hypothesis inconsistent with d
For each hypothesis g in G that is not consistent with d
Remove g from G
Add to G all minimal specializations h of g such that
h is consistent with d, and some member of S is more specific than h in G
ve from G any hypothesis that is less general than another hypothesis
KEY TAKEAWAYS
References:
1. Tom M. Mitchell, ―Machine Learning, McGraw-Hill Education (India) Private Limited, 2013.
2. Ethem Alpaydin, ―Introduction to Machine Learning (Adaptive Computation And Machine Learning), The MIT Press 2004.
3. Stephen Marsland, ―Machine Learning: An Algorithmic Perspective, CRC Press, 2009.
4. Bishop, C., Pattern Recognition, and Machine Learning. Berlin: Springer-Verlag.
UNIT 1
INTRODUCTION – Well defined learning problems
For any learning system, we must be knowing the three elements — T (Task), P (Performance Measure), and E (Training Experience). At a high level, the process of the learning system looks as below.
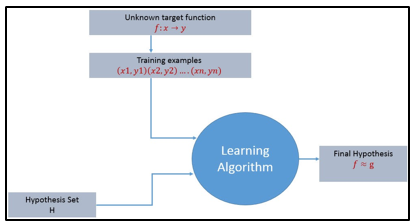
Figure.1 Learning process algorithm
The learning process starts with task T, performance measure P, and training experience E, and objective are to find an unknown target function. The target function is an exact knowledge to be learned from the training experience and its unknown. For example, in a case of credit approval, the learning system will have customer application records as experience and the task would be to classify whether the given customer application is eligible for a loan. So in this case, the training examples can be represented as (x1,y1)(x2,y2)..(xn,yn) where X represents customer application details and y represents the status of credit approval.
KEY TAKEAWAYS
The goal of the learning process is to design a learning system that follows the learning process, it requires considering a few design choices. The design choices are used to decide the key components:
1. Kind of training experience
2. The exact type of knowledge to be learned (it involves Choosing Target Function). At the initial stage, steps of target function are not known.
3. A detailed representation of target knowledge (Choosing a representation for the Target Function)
4. A learning mechanism (Choosing an approximation algorithm for the Target Function)
We will look into the checkers learning problem and apply the above design choices. For a checkers learning problem, the three elements will be,
1. Task T: To play checkers
2. Performance measure P: Total percent of the game won in the tournament.
3. Training experience E: A set of games played against itself
Training experience
During the design of the checker's learning system, the type of training experience available for a learning system will have a significant effect on the success or failure of the learning.
In the case of indirect training experience, the move sequences for a game and the final result (win, loss, or draw) are given for some games. How to assign credit or blame to individual moves is the credit assignment problem.
II. Teacher or Not — Supervised — The training experience will be labeled, which means, all the board states will be labeled with the correct move. So the learning takes place in the presence of a supervisor or a teacher.
Unsupervised — The training experience will be unlabelled, which means, all the board states will not have the moves. So the learner generates random games and plays against itself with no supervision or teacher involvement.
Semi-supervised — Learner generates game states and asks the teacher for help in finding the correct move if the board state is confusing.
III. Is the training experience good — Do the training examples represent the distribution of examples over which the final system performance will be measured.
Performance is best when training examples and test examples are from the same/a similar distribution.
The checker player learns by playing against oneself. Its experience is indirect. It may not encounter moves that are common in human expert play. Once the proper training experience is available, the next design step will be choosing the Target Function.
Choosing the Target Function
In this design step, we need to determine exactly what type of knowledge has to be learned and it's used by the performance program.
When you are playing the checkers game, at any moment, you decide on choosing the best move from different possibilities. You think and apply the learning that you have gained from the experience. Here the learning is, for a specific board, you move a checker such that your board state tends towards the winning situation. Now the same learning has to be defined in terms of the target function.
Here there are 2 considerations — direct and indirect experience.
During the direct experience, the checkers learning system, it needs only to learn how to choose the best move among some large search space. We need to find a target function that will help us choose the best move among alternatives. Let us call this function Choose Move and use the notation.
Choose Move: B →M to indicate that this function accepts as input any board from the set of legal board states B and produces as output some move from the set of legal moves M.
When there is an indirect experience, it becomes difficult to learn such a function. How about assigning a real score to the board state. So the function is V: B →R indicating that this accepts as input any board from the set of legal board states B and produces an output a real score. This function assigns the higher scores to better board states.
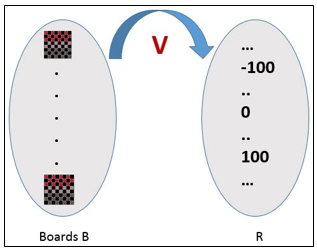
Figure 2
If the system can successfully learn such a target function V, then it can easily use it to select the best move from any board position.
Let us, therefore, define the target value V(b) for an arbitrary board state b in B, as follows:
1. if b is a final board state that is won, then V(b) = 100
2. if b is a final board state that is lost, then V(b) = -100
3. if b is a final board state that is drawn, then V(b) = 0
4. if b is not a final state in the game, then V (b) = V (b’), where b’ is the best final board state that can be achieved starting from b and playing optimally until the end of the game.
The (4) is a recursive definition and to determine the value of V(b) for a particular board state, it performs the search ahead for the optimal line of play, all the way to the end of the game. So this definition is not efficiently computable by our checkers playing program, we say that it is a non-operational definition.
The goal of learning, in this case, is to discover an operational description of V; that is, a description that can be used by the checkers-playing program to evaluate states and select moves within realistic time bounds.
It may be very difficult in general to learn such an operational form of V perfectly. We expect learning algorithms to acquire only some approximation to the target function ^V.
Choosing a representation for the Target Function
Now it's time to choose a representation that the learning program will use to describe the function ^V that it will learn. The representation of ^V can be as follows.
To keep the discussion simple, let us choose a simple representation for any given board state, the function ^V will be calculated as a linear combination of the following board features:
^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
Where w0 through w6 are numerical coefficients or weights to be obtained by a learning algorithm. Weights w1 to w6 will determine the relative importance of different board features.
Specification of the Machine Learning Problem at this time — Till now we worked on choosing the type of training experience, choosing the target function and its representation. The checkers learning task can be summarized as below.
Task T: Play Checkers
Performance Measure: % of games won in the world tournament
Training Experience E: opportunity to play against itself
Target Function: V: Board → R
Target Function Representation : ^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
The first three items above correspond to the specification of the learning task, whereas the final two items constitute design choices for the implementation of the learning program.
Choosing an approximation algorithm for the Target Function
Generating training data —
To train our learning program, we need a set of training data, each describing a specific board state b and the training value V_train (b) for b. Each training example is an ordered pair <b,V_train(b)>
For example, a training example may be <(x1 = 3, x2 = 0, x3 = 1, x4 = 0, x5 = 0, x6 = 0), +100">.
This is an example where black has won the game since x2 = 0 or red has no remaining pieces. However, such clean values of V_train (b) can be obtained only for board value b that are clear win, lose, or draw.
In the above case, assigning a training value V_train(b) for the specific boards b that are clean win, lose or draw is direct as they are direct training experience. But in the case of indirect training experience, assigning a training value V_train(b) for the intermediate boards is difficult. In such a case, the training values are updated using temporal difference learning. Temporal difference (TD) learning is a concept central to reinforcement learning, in which learning happens through the iterative correction of your estimated returns towards a more accurate target return.
Let Successor(b) denotes the next board state following b for which it is again the program’s turn to move. ^V is the learner’s current approximation to V. Using this information, assign the training value of V_train(b) for any intermediate board state b as below :
V_train(b) ← ^V(Successor(b))
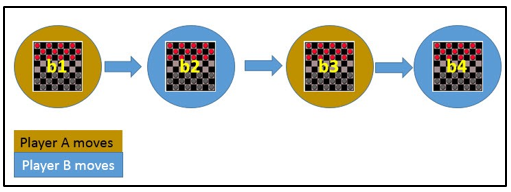
In the above figure, V_train(b1) ← ^V(b3), where b3 is the successor of b1. Once the game is played, the training data is generated. For each training example, the V_train(b) is computed.
Adjusting the weights
Now it's time to define the learning algorithm for choosing the weights and best fit the set of training examples. One common approach is to define the best hypothesis as that which minimizes the squared error E between the training values and the values predicted by the hypothesis ^V.
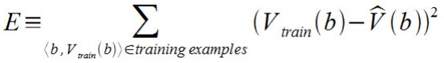
The learning algorithm should incrementally refine weights as more training examples become available and it needs to be robust to errors in training data
Least Mean Square (LMS) training rule is the one training algorithm that will adjust weights a small amount in the direction that reduces the error.
The LMS algorithm is defined as follows:

Final Design for Checkers Learning system
KEY TAKEAWAYS
Here there are 2 considerations — direct and indirect experience.
^V = w0 + w1 · x1(b) + w2 · x2(b) + w3 · x3(b) + w4 · x4(b) +w5 · x5(b) + w6 · x6(b)
Leave advanced mathematics to the experts. As you embark on a journey with ML, you’ll be drawn into the concepts that build the foundation of science, but you may still be on the other end of results that you won’t be able to achieve after learning everything. Fortunately, the experts have already taken care of the more complicated tasks and algorithmic and theoretical challenges. With this help, mastering all the foundational theories along with statistics of an ML project won’t be necessary.
Once you become an expert in ML, you become a data scientist. For those who are not data scientists, you don’t need to master everything about ML. All you have to do is to identify the issues which you will be solving and find the best model resources to help you solve those issues.
For example, for those dealing with basic predictive modeling, you wouldn’t need the expertise of a master in natural language processing. Why would you spend time being an expert in the field when you can just master the niches of ML to solve specific problems?
ML algorithms will always require much data when being trained. Often, these ML algorithms will be trained over a particular data set and then used to predict future data, a process that you can’t easily anticipate. The previously “accurate” model over a data set may no longer be as accurate as it once was when the set of data changes. For a system that changes slowly, the accuracy may still not be compromised; however, if the system changes rapidly, the ML algorithm will have a lesser accuracy rate given that the past data no longer applies.
ML algorithms can pinpoint the specific biases which can cause problems for a business. An example of this problem can occur when a car insurance company tries to predict which client has a high rate of getting into a car accident and tries to strip out the gender preference given that the law does not allow such discrimination. Even without gender as a part of the data set, the algorithm can still determine the gender through correlates and eventually use gender as a predictor form.
Developers always use ML to develop predictors. Such predictors include improving search results and product selections and anticipating the behavior of customers. One reason behind inaccurate predictions may be overfitting, which occurs when the ML algorithm adapts to the noise in its data instead of uncovering the basic signal.
ML algorithms running over fully automated systems have to be able to deal with missing data points. One popular approach to this issue is using the mean value as a replacement for the missing value. This application will provide reliable assumptions about data including the particular data missing at random.
Whether they’re being used in automated systems or not, ML algorithms automatically assume that the data is random and representative. However, having random data in a company is not common.
The best way to deal with this issue is to make sure that your data does not come with gaping holes and can deliver a substantial amount of assumptions.
Recommendation engines are already common today. While some may be reliable, others may not seem to be more accurate. ML algorithms impose what these recommendation engines learn. One example can be seen when a customer’s taste changes; the recommendations will already become useless. Experts call this phenomenon the “exploitation versus exploration” trade-off. In the event the algorithm tries to exploit what it learned devoid of exploration, it will reinforce the data that it has, will not try to entertain new data, and will become unusable.
To deal with this issue, marketers need to add the varying changes in tastes over time-sensitive niches such as fashion. With this step, you can avoid recommending winter coats to your clients during the summer.
KEY TAKEAWAYS
The Learning Task
Given: Instances X: a set of items over which the concept is defined.
Hypotheses H: the conjunction of constraints on attributes.
Target concept c: c : X → {0, 1}
Training examples (positive/negative): <x,c(x)>
Training set D: available training examples
Determine: i A hypothesis h in H such that h(x) = c(x), for all x in X
More_general_than_or_equal_to relation
hj ≥ g hk ⇔ (∀x∈X)[(hk(x) =1)→(hj(x) =1)]
(Strictly) more_general_than relation
<Sunny,?,?,?,?,?> >g <Sunny,?,?,Strong,?,?>
More_General_Than Relation
1. Initialize h to the most specific hypothesis in H
2. For each positive training example x For each attribute constraint ai in h If the constraint ai is satisfied by x Then do nothing Else replace ai in h by the next more general constraint satisfied by x
3. Output hypothesis h
Hypothesis Space Search by Find-S
Properties of Find-S Ignores every negative example (no revision to h required in response to negative examples). Why? What’re the assumptions for this? Guaranteed to output the most specific hypothesis consistent with the positive training examples (for conjunctive hypothesis space). Final h also consistent with negative examples provided the target c is in H and no error in D
The List-Then-Eliminate algorithm initializes the version space to contain all hypotheses in H, then eliminates the inconsistent hypotheses, from training examples. The version space of hypotheses thus shrinks as more examples are observed until one hypothesis remains that is consistent with all the observed examples.
Presumably, this hypothesis is the desired target concept. If the data available is insufficient, to narrow the version space to a single hypothesis, then the algorithm can output the entire set of hypotheses consistent with the observed data.
The List-Then-Eliminate algorithm can be applied whenever the hypothesis space “H” is finite.
It has many advantages, including the fact that it is guaranteed to output all hypotheses consistent with the training data.
It requires exhaustively enumerating all hypotheses in H — an unrealistic requirement for all but the most trivial hypothesis spaces.
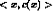
remove from
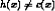
Candidate-Elimination Algorithm part 2
If d is a negative example
Remove from S any hypothesis inconsistent with d
For each hypothesis g in G that is not consistent with d
Remove g from G
Add to G all minimal specializations h of g such that
h is consistent with d, and some member of S is more specific than h in G
ve from G any hypothesis that is less general than another hypothesis
KEY TAKEAWAYS
References:
1. Tom M. Mitchell, ―Machine Learning, McGraw-Hill Education (India) Private Limited, 2013.
2. Ethem Alpaydin, ―Introduction to Machine Learning (Adaptive Computation And Machine Learning), The MIT Press 2004.
3. Stephen Marsland, ―Machine Learning: An Algorithmic Perspective, CRC Press, 2009.
4. Bishop, C., Pattern Recognition, and Machine Learning. Berlin: Springer-Verlag.