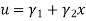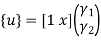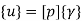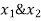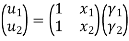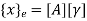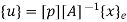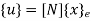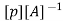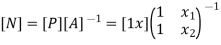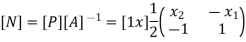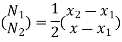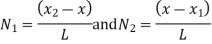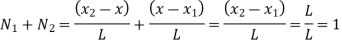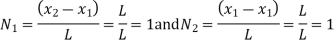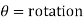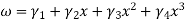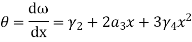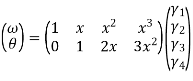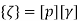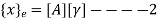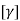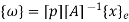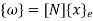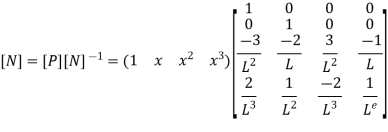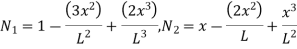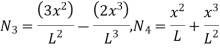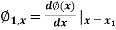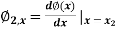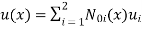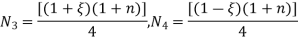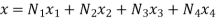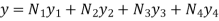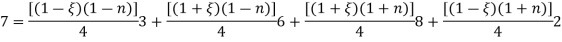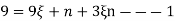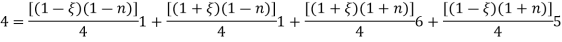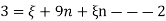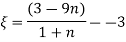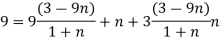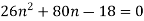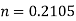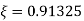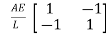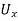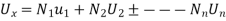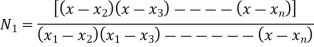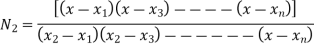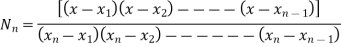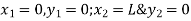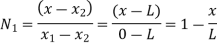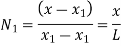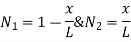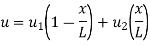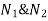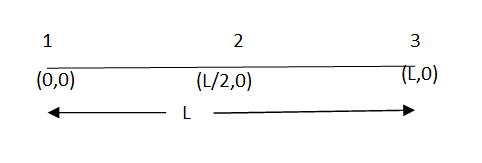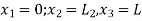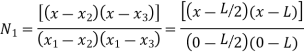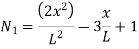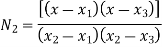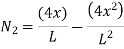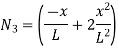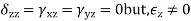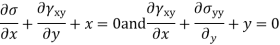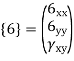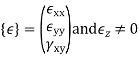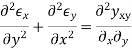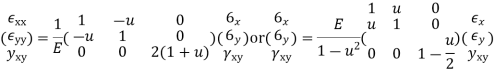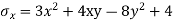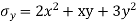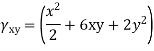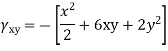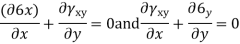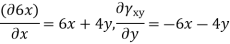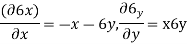UNIT-4
Pascal's triangle law for 2D shape functions polynomial
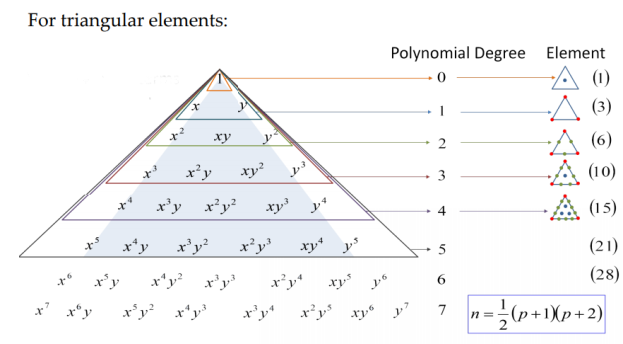
1) For triangular elements:
|
Fig.1 Pascal's triangle for triangular elements
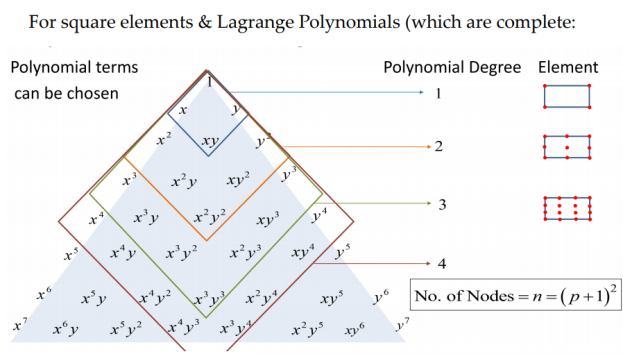
2) For square elements:
|
Fig.2 Pascal's triangle for square elements
Serendipity Polynomials
- These functions are similar to Lagrangian polynomials, but for their incompleteness (missing terms). Due to this fact we do not need to introduce additional inner nodes, as for Lagrangian polynomials of higher order.
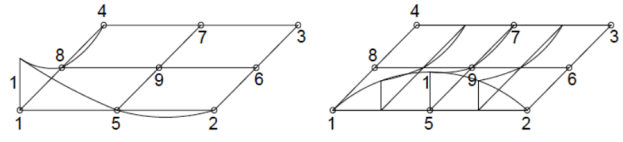
Lagrange Polynomials
|
Fig.3 Lagrange Polynomials
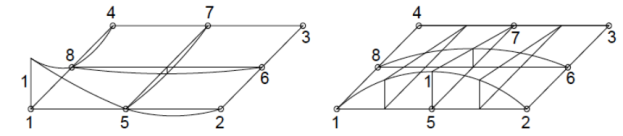
Serendipity Polynomials
|
Fig.4 Serendipity Polynomials
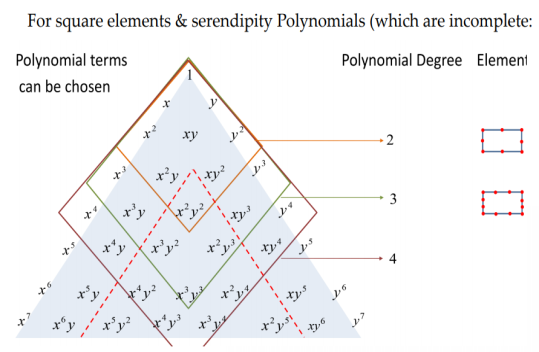
3) For square elements & serendipity Polynomials
|
Fig.5 Pascal's triangle for square elements & serendipity Polynomials
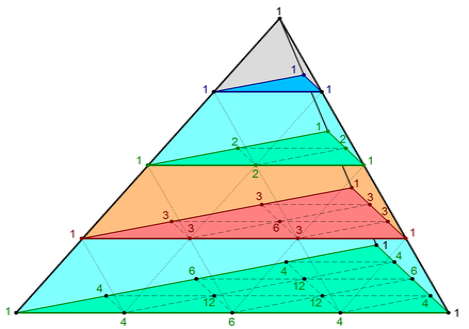
- In mathematics, Pascal's pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution.
- Pascal's Pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial numbers and relates to the binomial expansion and the binomial distribution.
- The binomial and trinomial numbers, coefficients, expansions, and distributions are subsets of the multinomial constructs with the same names.
|
Fig.6 Pascal's triangle for 3D tetrahedron
- Because the tetrahedron is a three-dimensional object, displaying it on a piece of paper, a computer screen or other two-dimensional medium is difficult.
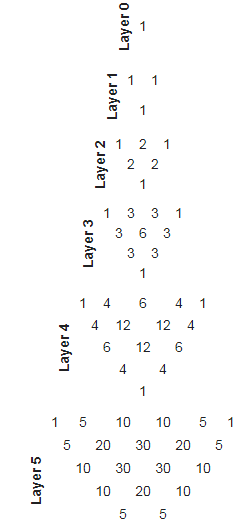
- Assume the tetrahedron is divided into a number of levels, or floors, or slices, or layers. The top layer (the apex) is labelled "Layer 0". Other layers can be thought of as overhead views of the tetrahedron with the previous layers removed. The first six layers are as follows:
|
- There is three-way symmetry of the numbers in each layer.
- The number of terms in the
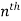 Layer is the
Layer is the 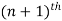 triangular number:
triangular number: 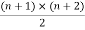
- The sum of the values of the numbers in the
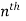 Layer is .
Layer is .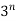
- Each number in any layer is the sum of the three adjacent numbers in the layer above.
- Each number in any layer is a simple whole number ratio of the adjacent numbers in the same layer.
- Each number in any layer is a coefficient of the Trinomial Distribution and the trinomial expansion. This non-linear arrangement makes it easier to:
1) Display the trinomial expansion in a coherent way
2) Compute the coefficients of the Trinomial Distribution
3) Calculate the numbers of any Tetrahedron layer.
- The numbers along the three edges of the nth Layer are the numbers of the nth Line of Pascal's triangle. And almost all the properties listed above have parallels with Pascal's triangle and Multinomial Coefficients.
Derivation for linear simplex element
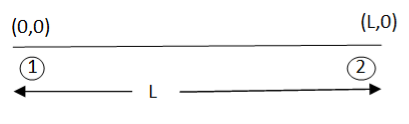
1. Shape function for two noded bar element in (x,y) co-ordinates
Let consider two noded bar element of length l. 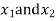 are the cartesian co-ordinates of nodes 1& 2 respectively.
are the cartesian co-ordinates of nodes 1& 2 respectively. 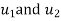 are displacement of nodes 1 and 2 u is the displacement of any point in x-directions.
are displacement of nodes 1 and 2 u is the displacement of any point in x-directions.
1 2
|
Fig.7
Total DoF =02 (one at each node)
In matrix form,
Where, [p]= parametric matrix II. Displacement function in terms of nodal displacement Express displacement function in terms of nodal displacement using the co-ordinates of nodes
Where ,[A]= connectivity matrix Obtained
Where [N]= shape function [N]= III. shape function :-
Inverse is obtained by using method of adjoin
Sum of shape functions is always unity
At node 2, x=
|
Shape function for two noded beam element (bending element)
Let consider two noded beam element of length L, flexural rigidity EL. Degree of freedom at each of the beam element are two(translation and rotation)
Total Dof are 04 w= translation
In matrix form
Where [p]= parametric matrix II. Displacement function in terms of nodal displacement Express displacement function in terms of nodal displacement using the coordinates of nodes x=0 at node 1 and x=L at node 2
Where [A]= connectivity matrix Obtaining We get,
Where [N]= shape function III. Shape functions
Inverse of [A] is obtained using elementary operations of matrix algebra
At node 1;x=0 N1=1 , N2=0 , N3=0 , N4=0 At node,x=L N1=0 , N2=0 , N3=1 , N4=0
|
- Lagrangian polynomials and serendipity functions provide a
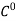 continuity. If we additionally need continuity of the first derivatives between the finite elements we use Hermition polynomials.
continuity. If we additionally need continuity of the first derivatives between the finite elements we use Hermition polynomials. - A Hermition polynomial of the order n,
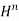 (x), is a 2n+1 order Polynomial. For example a Hermitian polynomial of the first order is actually a third order polynomial.
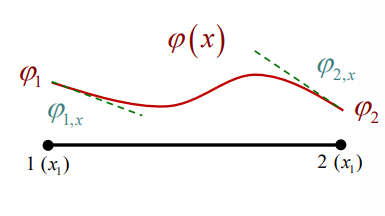
(x), is a 2n+1 order Polynomial. For example a Hermitian polynomial of the first order is actually a third order polynomial. - Let us consider a bar element with nodes on its ends. Unknowns are values of the function φ in the nodes 1 and 2, φ1 and φ2, and first derivatives of φ in respect to x , φ1,x and φ2,x
|
Fig.8 (a)Hermition polynomial
|
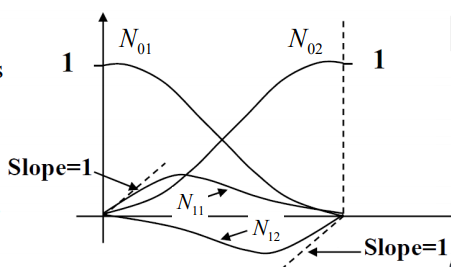
- Remember: The 1st derivative of displacement corresponds to rotation.
- Hermitian shape functions relate not only the displacements at nodes to displacements within the elements but also to the first order derivatives (e.g. rotational DOFs for a beam element).
- Shape function of u(x) and Shape function of the derivative u’(x)
|
Fig.8 (b)Hermition polynomial
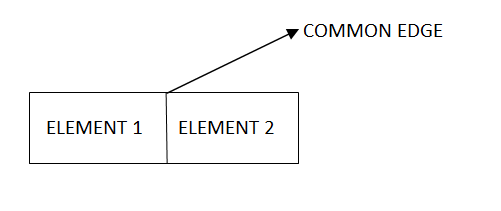
1) Displacement function must be continuous and compatible within elements.
Continuous-
Second element should start by taking one edge common of first element.
|
Fig.9
Compatible-
When it deforms, there should not be any discontinuity between elements i.e. Elements must not separate and overlap and there should not be any sudden change in slope across the inter element boundaries.
2) The displacement function must be capable of representing constant strain state within the elements. This will have achieved by dividing structure into smaller and smaller elements.
3) The displacement function must be capable of representing rigid body displacement, i.e.,when nodes are given such displacement under rigid body motion, elements should not experience any strain and hence leads to zero nodal force .Constant term in polynomial ensures this condition.
- That is the displacement shapes will not change with a change in local coordinate system.
- This property is known as geometric isotropy, or geometric invariance.
- Thus, geometric invariance can be achieved by selecting the corresponding order of terms on either side of the axis of symmetry.
Basic theorems of isoparametric elements
Theorem 1-
If two adjusted elements are generated using shape functions, then there is continuity at the common edge.
Theorem 2-
It states, if the shape functions used are such that continuity of displacement is represented in the parent coordinates then the continuity requirement will be satisfied in the isoparametric elements also.
Theorem 3-
The constant strain condition and constant derivative condition satisfied by all isoparametric elements
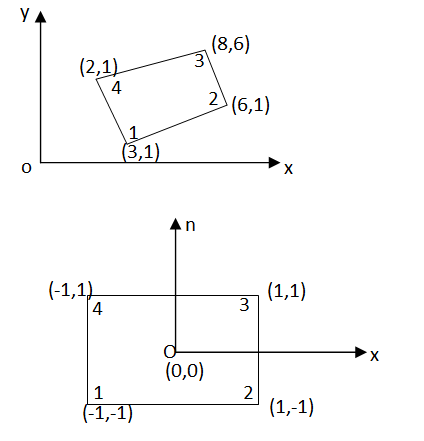
Example –
For the isoparamatric quadrilateral element shown in fig. determine co-ordinate of the point ‘Q’ which has cartesian coordinates (7,4)
|
Fig.10
Solution –
Parent element for the quadrilateral in natural co-ordinates system in four noded rectangle. Shape functions for the four noded rectangular element in natural co-ordinates system are-
Cartesian coordinates of point ‘p’ are
Given p(x,y) =p(7,4)
From eq. 1
Put into the eq. 2
Put this value in eq. 3
|
Element stiffness matrix-
- The stiffness matrix is an inherent property of the structure. Element stiffness is obtained with respect to its axes and then transformed this stiffness to structure axes.
- The characteristics of stiffness matrix are as follows-
1) Stiffness matrix is symmetric and square.
2) In stiffness matrix, all diagonal elements are positive.
3) Stiffness matrix is positive definite.
Global Stiffness matrix –
- A structural system is an assemblage of number of elements.
- These elements are interconnected together to form the whole structure.
- Therefore, the element stiffness of all the elements are first need to be calculated and then assembled together in systematic manner.
- This matrix is called is global stiffness matrix.
Stiffness matrix for two noded bar element-
K=
|
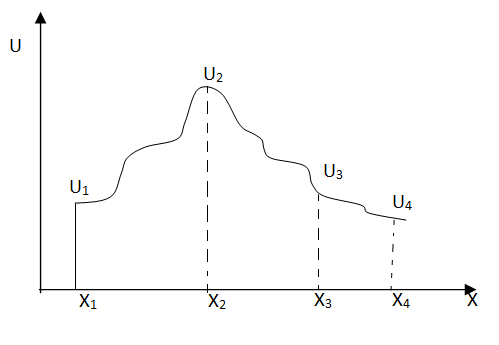
Langrange’s interpolation formula
Suppose we have a function which when plotted behaves as shown in fig.
|
Fig.11
Suppose we want to find Now,
Where,
Note:- shape function has a unit value at one nodal point (for which it is calculated) & zero value at all other nodal points.
|
Simple exercise-
- Two nodal truss element
|
Fig.12
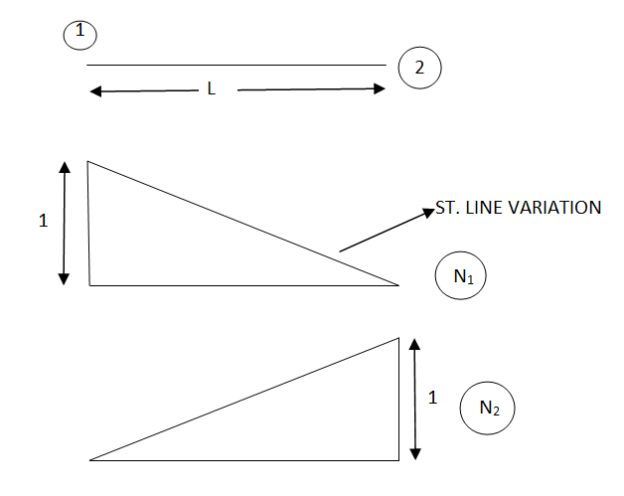
Variation of shape function
|
|
Fig.13
2. Three nodal truss element.
|
Fig.14
Similarly
|
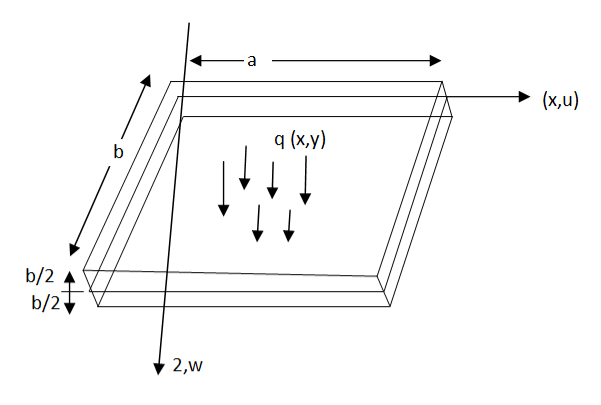
Two dimensional elasticity problems under the following conditionsare considered as plane stress problem
- One dimensional is very small as compared to other two dimensions eg. Rectangular plate(thickness is very small as compared to length and width)
- The loads acting on the body are in the plane perpendicular to the thickness of the body
i.e z-axis the load are uniformly disturbed over the thickness
3. The stress is the small direction (normally z) must be zero
|
|
Fig.15
Equations of equilibrium
State of stress at a point
State of strain at a point
Strain -displacement relationship
Stress strain relation
Que – show that the following state of stress Ps in equilibrium
Sol- differential equation of equilibrium of 2D elasticity problem is given by
Putting these differential quantities in equations of equilibrium 1 and satisfying those. This proves that given state of stress is in equilibrium.
|
References-
(1) Finite Element Analysis -C.S. Krishnanmoorthy, Tata McGraw Hill Publishing Co. Ltd, New Delhi,
(2) The Finite Element method -ZIENKIEWICZ.O.C.Tata McGraw Hill Pub. New Delhi, 2000
(3) Finite Element Methods by C R Alaval , PHI
(4) Finite Elements in Engineering:- Chandrupatta, et. AI. Prentice Hall of India Pvt. Ltd.,