Unit-3
Sequences and Series
Sequence –
A function f: N 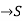 , where S is a non-empty set , is called sequence , for each nϵN.
, where S is a non-empty set , is called sequence , for each nϵN.
The sequence is written as f(1) , f(2) , f(3) , f(4)……….f(n).
Any sequence f(n) can be denoted as <f(n)> or {f(n)} or (f(n)).
Suppose f(n) = 
Then it can be written as - 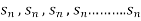 and can be denoted as <
and can be denoted as < >or {
>or {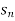 } or (
} or ( )
)
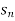 is the n’th term of the sequence.
is the n’th term of the sequence.
Example: suppose we have a sequence – 1 , 4 , 9 , 16 ,……….. and its n’th term is 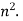
This sequence can be written as -<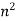 >
>
Example: 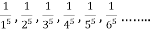 its n’th term will be
its n’th term will be  .and can be written as <
.and can be written as < >
>
Types of sequences –
1. Finite sequence- A sequence which has finite number of terms is called finite sequence.
2. Infinite sequence- A sequence which is not finite , called infinite sequence.
Limit of a Sequence- A sequence < > is said to tend to limit “l” , when given any positive number ‘ϵ’ , however small , we can always find a integer ‘m’ such that |
> is said to tend to limit “l” , when given any positive number ‘ϵ’ , however small , we can always find a integer ‘m’ such that | 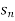 – l| <ϵ , for every for all, n ≥ m , and we can define this as follows,
– l| <ϵ , for every for all, n ≥ m , and we can define this as follows,
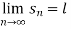
Example: If 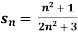 , then the limit of
, then the limit of  will be,
will be,
 =
= 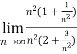 =
= 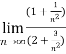 = ½
= ½
Hence the limit of the sequence is 1/2.
Some important limits to remember-
1.
2. 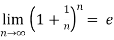
3. 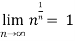
4. 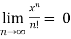

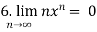
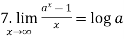
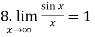
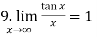
Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Oscillatory sequence- when a sequence neither converges nor diverges then it is called oscillatory sequence.
Note- A sequence which neither converges nor diverges, is called oscillatory sequence.
A sequence converges to zero is called null.
Example-1: Consider a sequence 2, 3/2 , 4/3 , 5/4, …….. here Sn = 1 + 1/n
Sol. As we can see that the sequence Sn is convergent and has limit 1.
According to def.
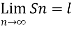
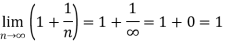
Example-2: Consider a sequence Sn= n² + (-1)ⁿ.
Sol. Here we can see that, the sequence Sn is divergent as it has infinite limit.

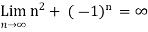
Example: Suppose 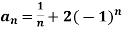 , here the sequence is said to be oscillate. Because it is between -2 and 2.
, here the sequence is said to be oscillate. Because it is between -2 and 2.
Series
Infinite series- If 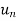 is a sequence , then
is a sequence , then 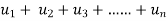 is called the infinite series.
is called the infinite series.
It is denoted by 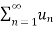 .
.
Examples of infinite series-
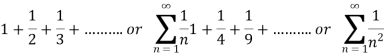
Key takeaways-
Covergent series - Suppose n→∞ , Sn→ a finite limit ‘s’ , then the seires Sn is said to be convergent .
We can denote it as,
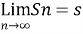
Divergent series- When Sn tends to infinity then the series is said to be divergent.
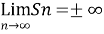
Oscillatory series- When Sn does not tends to a unique limit (finite or infinite) , then it is called Oscillatory series.
Properties of infinite series –
1. The convergence and divergence of an infinite series is unchanged addition or deletion of a finite number of term from it.
2. If positive terms of convergent series change their sign , then the series will be convergent.
3. Let 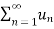 converges to s , let k be a non-zero fixed number then
converges to s , let k be a non-zero fixed number then 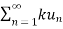 converges to ks.
converges to ks.
4. Let 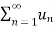 converges to ‘l’ and
converges to ‘l’ and 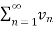 converges to ‘m’.
converges to ‘m’.
Example-1: Check whether the series 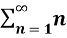 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. As we know that,
Sn = 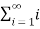
Therefore,
Sn = 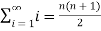
Now find out the limit of the sequence,
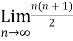 = ∞
= ∞
Here the value of the limit is infinity, so that the series is divergent as sequence diverges.
Example-2: Check whether the series 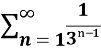 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. The general formula for this series is given by,
Sn = 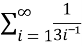 =
= 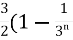 )
)
We get,
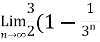 ) = 3/2
) = 3/2
Hence the series is convergent and its values is 3/2.
Example-3: check whether the series 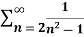 is convergent or divergent.
is convergent or divergent.
Sol. The general formula can be written as,
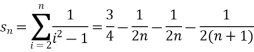
We get on applying limits,
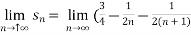 ) = 3/4
) = 3/4
This is the convergent series and its value is 3 / 4
Example-4: Check whether the following series is convergent or divergent. If convergent, find its value.
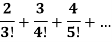
Sol. n’th term of the series will be,
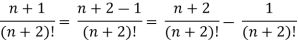
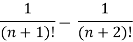
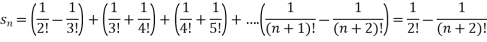

General properties of series
The general properties of series are-
1. The nature of a series does not change by multiplication of all terms by a constant k.
2. The nature of a series does not change by adding or deleting of a finite number of terms.
3. If two series 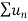 and
and 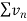 are convergent, then
are convergent, then 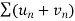 is also convergent.
is also convergent.
Exampple-1: Prove that the following series is convergent and find its sum.
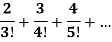
Sol. Here,
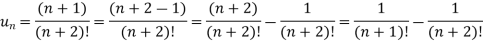
And
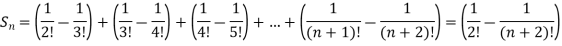
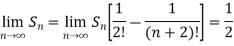
Hence the series is convergent and the limit is 1/2 .
Example-2: Test the convergence of the series- 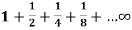
Sol. Here we can see that the given series is in geometric progression
As its first term is 1 and common ratio is ½.
Then we know that the sum of n terms of a geometric progression is-
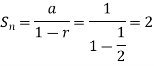
Hence the limit will be-
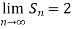
So that the series is convergent.
Key takeaways-
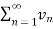
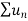
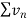

Comparison tests
If all the terms in an infinite series are positive after few negative terms , then the series said to be a positive term series.
Suppose ,
-22-65+ 55 +69 99+125+………….is a positive term series.
If we remove these negative terms, then the nature of the series does not change.
Comparison test-
Statement-
Suppose we have two series of positive terms 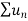 and
and 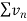 then,
then,
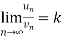 , where k is a finite number , then both series converges or diverges together.
, where k is a finite number , then both series converges or diverges together.
Proof- we know that by the definition of limits, there exist a positive number epsilon(ε)
Which is very small. Such that
According to definition( comparison test)
|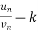 |<ε for n>m , that means
|<ε for n>m , that means
k-ε<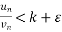 for n>m
for n>m
ignoring the first m terms of the series,
we get
k-ε<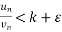 for n>m for all n ………………..(1)
for n>m for all n ………………..(1)
there will be two cases-
case-1: 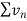 is convergent , then
is convergent , then
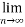 (
(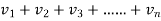 ) = r (say) , where r is finite number
) = r (say) , where r is finite number
From (1),
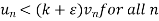
 (
( )<
)<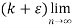 (
(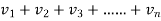 ) =
) = 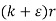
Therefore  is also convergent.
is also convergent.
Case-2: : is divergent, then
is divergent, then
 (
(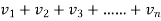 )→∞ …………………………..(2)
)→∞ …………………………..(2)
From eq. (1)

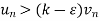
Then
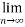 (
(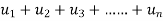 )<
)<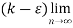 (
(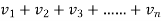 )
)
From(2)
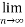 (
(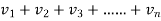 )→∞
)→∞
Hence, 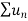 is also divergent.
is also divergent.
Example: Test the convergence of the following series.
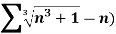
Sol. We have 
First we will find 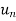 and the
and the 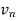

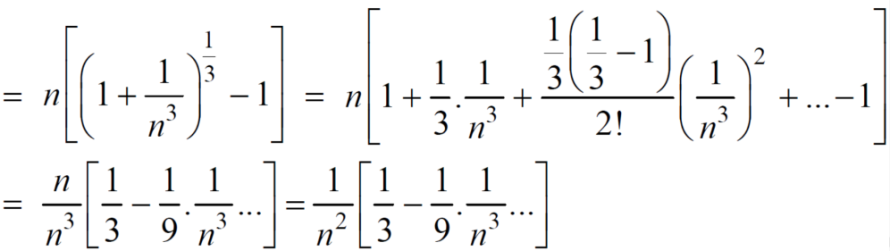
And

Here, we can see that, the limit is finite and not zero,
Therefore, 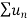 and
and 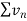 converges or diverges together.
converges or diverges together.
Since 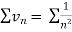 is of the form
is of the form  where p = 2>1
where p = 2>1
So that , we can say that,
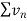 is convergent , so that
is convergent , so that 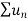 will also be convergent.
will also be convergent.
Example: Test the convergence of the following series-
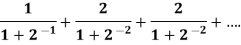
Sol. Here we have the series,
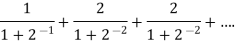
Now,
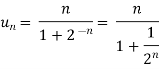
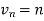
Now comapare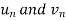

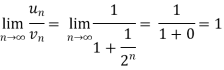
We can see that the limit is finite and not zero.
Here  and
and  converges or diverges together since ,
converges or diverges together since ,
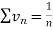 is the form of
is the form of 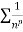 here p = 1,
here p = 1,
So that,
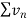 is divergent then
is divergent then 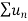 is also divergent.
is also divergent.
Example: Show that the following series is convergent.
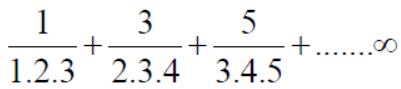
Sol.
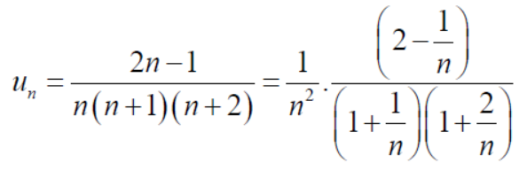
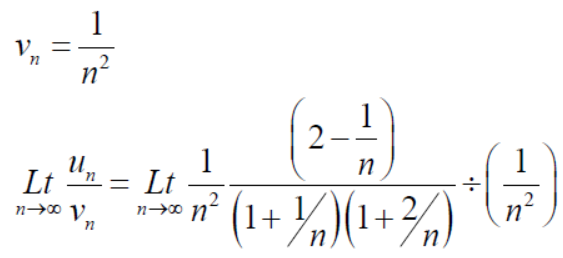
Suppose,
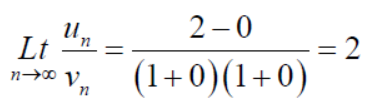

Which is finite and not zero.
By comparison test 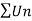 and
and 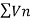 converge or diverge together.
converge or diverge together.
But,
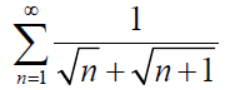
Is convergent. So that  is also convergent.
is also convergent.
Example: Test the series:
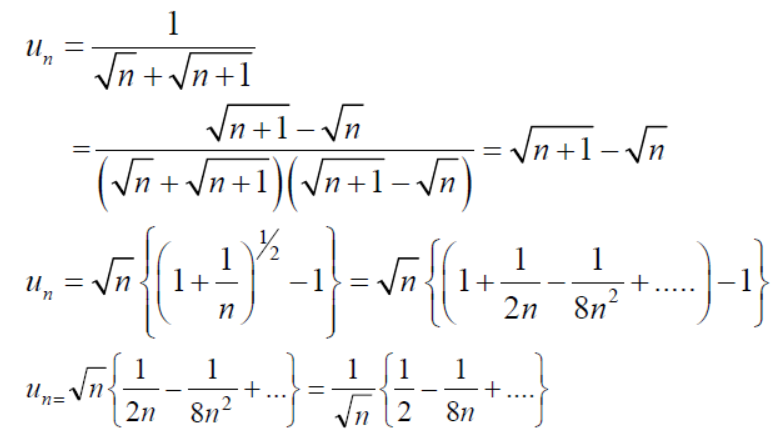
Sol. The series is,
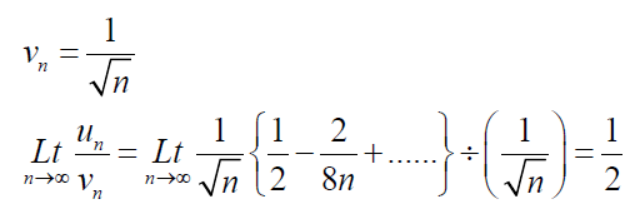
Now,
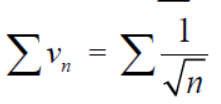
Take,
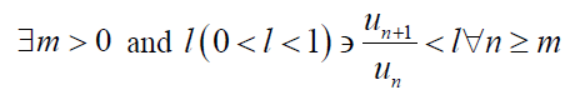
Which is finite and not zero.
Which is finite and not zero.
By comparison test 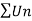 and
and  converge or diverge together.
converge or diverge together.
But,
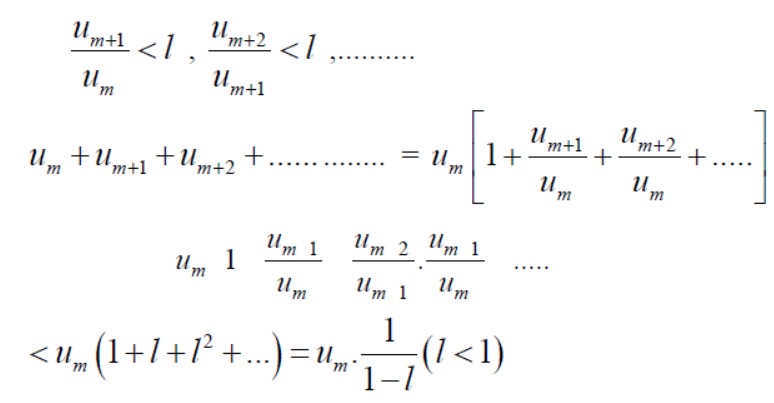
Is divergent. ( p = ½)
So that  is divergent.
is divergent.
Key takeaways-
Suppose we have two series of positive terms 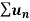 and
and  then,
then,
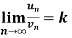 , where k is a finite number , then both series converges or diverges together.
, where k is a finite number , then both series converges or diverges together.
Ratio test-
Statement- suppose 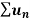 is a series of positive terms such that
is a series of positive terms such that 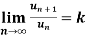 then,
then,
1. if k<1 , the series will be convergent.
2. if k>1 , then the series will be divergent.
Proof:
Case-1:
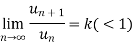
We know that from the definition of limits ,it follows,
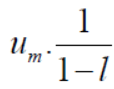
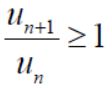
But,

Is the finite quantity. So 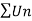 is convergent.
is convergent.
Case-2: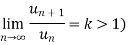
There could be some finite terms in starting which will never satisfy the condition,
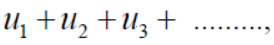
In this case we can find a number ‘m’,
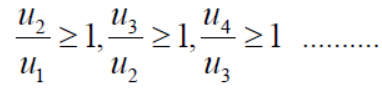
Ignoring the first ‘m’ terms, if we write the series as
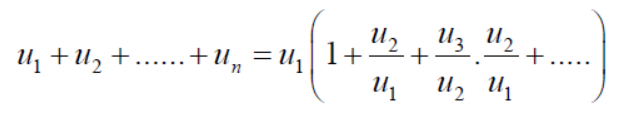
We have , in this case

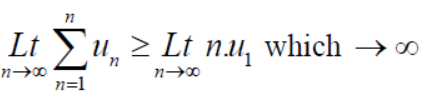

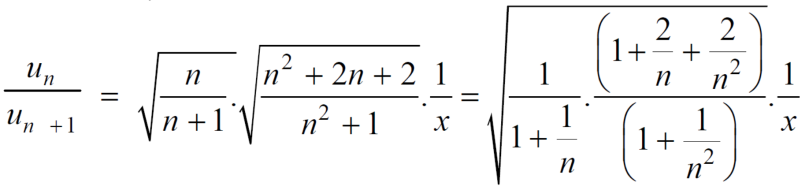
So that  is divergent.
is divergent.
Example: Test the convergence of the series whose n’th term is given below-
n’th term = 
Sol. We have
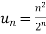 and
and 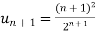
By D’Alembert ratio test,
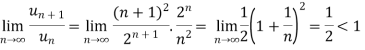
So that by D’Alembert ratio test , the series will be convergent.
Example: Test for the convergence of the n’th term of the series given below-
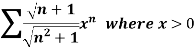
Sol. We have ,


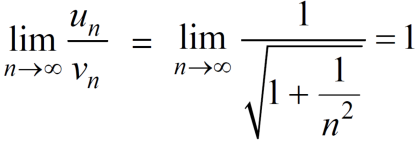
Now , by D’Almbert ratio test 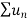 converges if
converges if 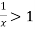 and diverges if
and diverges if 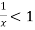
At x = 1 , this test fails.
Now , when x = 1
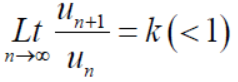
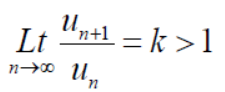
The limit is finite and not zero.
Then by comparison test, 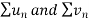 converges or diverges together.
converges or diverges together.
Since 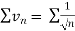 is the form of
is the form of 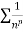 , in which
, in which 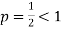
Hence 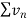 diverges then
diverges then  will also diverge.
will also diverge.
Therefore in the given series 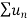 converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.
D-Alembert’s ratio test
Statement- suppose 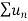 is a series of positive terms such that
is a series of positive terms such that 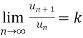 then,
then,
1. if k<1 , the series will be convergent.
2. if k>1 , then the series will be divergent.
Proof: Proof:
Case-1:

We know that from the definition of limits ,it follows,
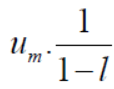
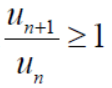
But,
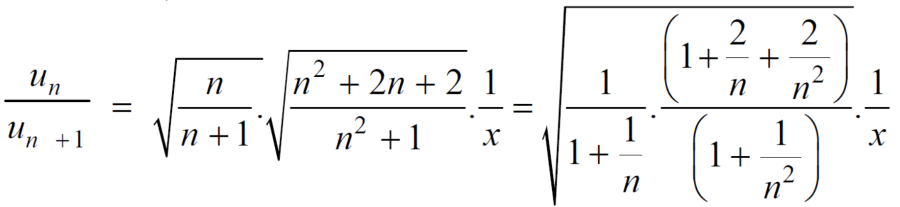
Is the finite quantity. So 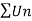 is convergent.
is convergent.
Case-2:
There could be some finite terms in starting which will never satisfy the condition,
In this case we can find a number ‘m’,
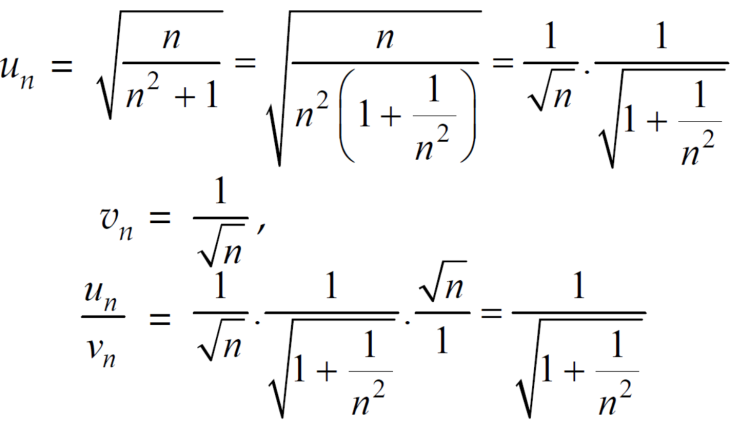
Ignoring the first ‘m’ terms, if we write the series as
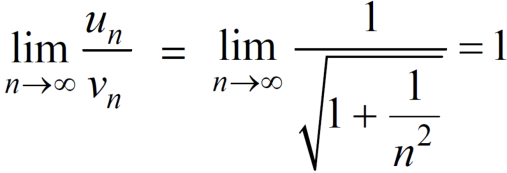
We have , in this case

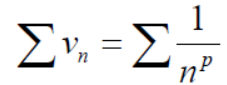
So that  is divergent.
is divergent.
Example: Test the convergence of the series whose n’th term is given below-
n’th term = 
sol. We have 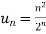 and
and 
byD’Alembert ratio test,

So that by D’Alembert ratio test , the series will be convergent.
Example: Test for the convergence of the n’th term of the series given below-
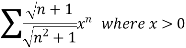
Sol. We have ,
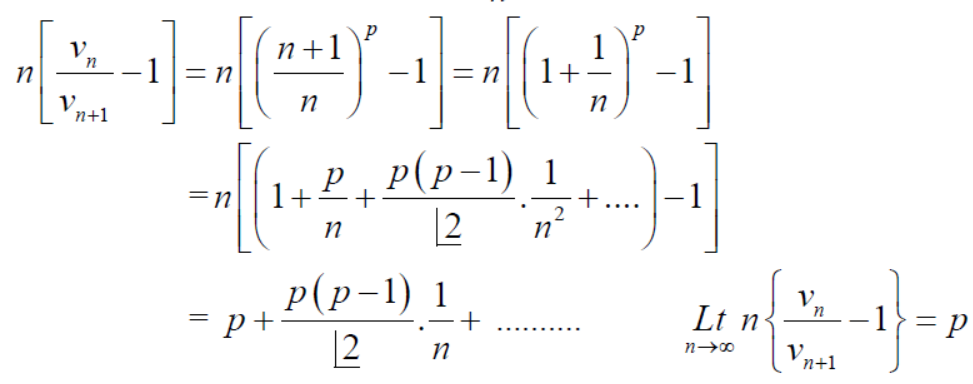
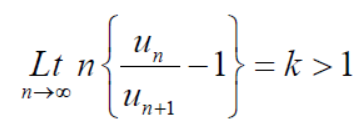
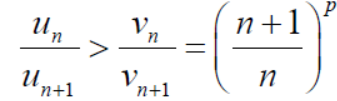
Now , by D’Almbert ratio test  converges if
converges if  and diverges if
and diverges if 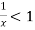
At x = 1 , this test fails.
Now , when x = 1
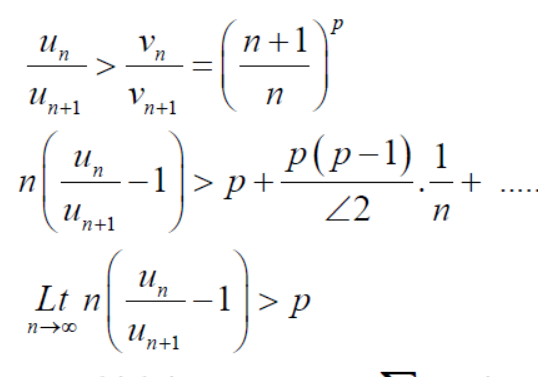
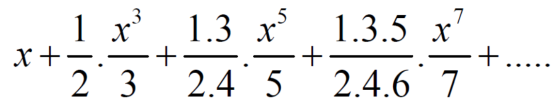
The limit is finite and not zero.
Then by comparison test,  converges or diverges together.
converges or diverges together.
Since 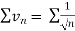 is the form of
is the form of 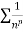 , in which
, in which 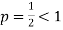
Hence 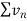 diverges then
diverges then 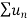 will also diverge.
will also diverge.
Therefore in the given series 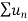 converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.
Raabe’s test
Let 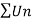 be a series of positive terms and
be a series of positive terms and
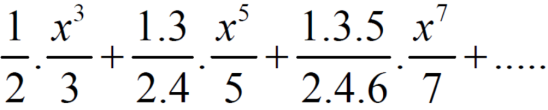
Then,
(1) if k >1 , 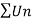 is convergent and
is convergent and
(2) if k < 1 , then 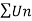 is divergent
is divergent
(3) this test fails if k = 1.
Proof: let us consider the series,

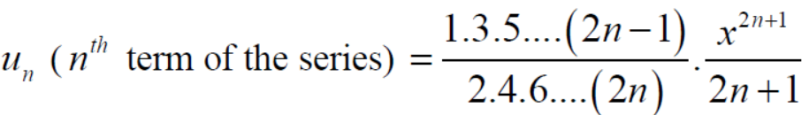
Case-1: in this case,
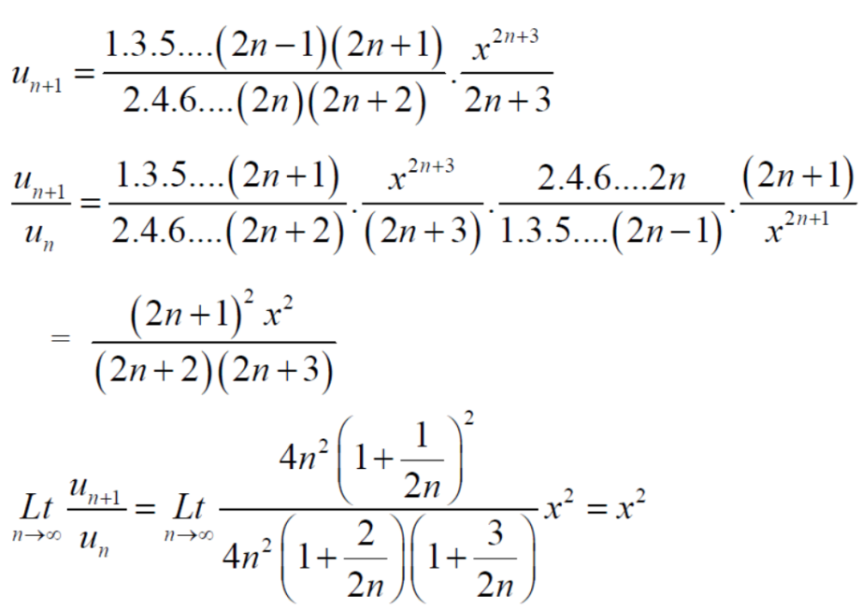
We choose a number ‘p’ for all k > p >1 , comparing thr series  with
with  which is divergent ,
which is divergent ,
We get  will converge if after some fixed numver of terms ,
will converge if after some fixed numver of terms ,
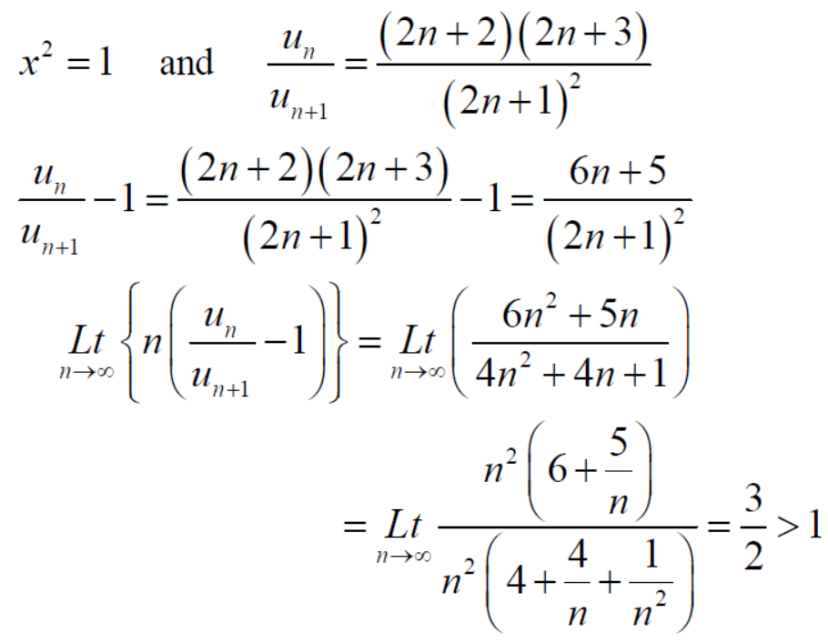
That means,
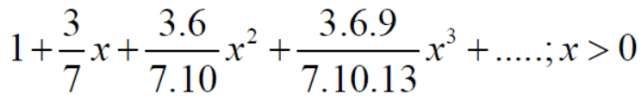
If k >p , which Is true . hence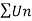 is convergent.
is convergent.
We can prove the second case similarly.
Example-1: Test the convergence of the following series.
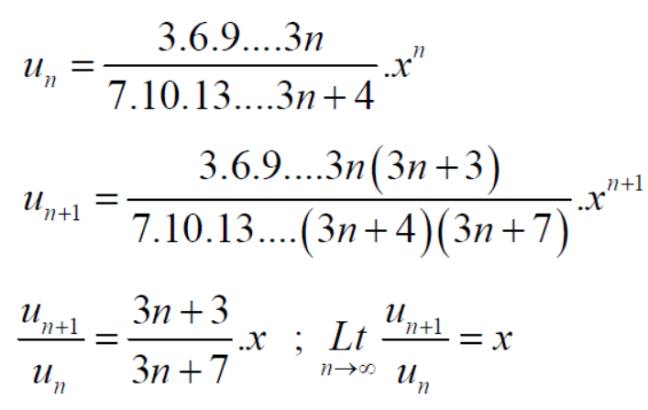
Sol. Neglecting the first term the series can be written as,
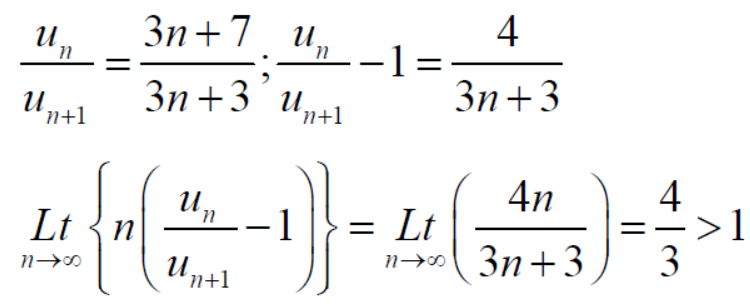
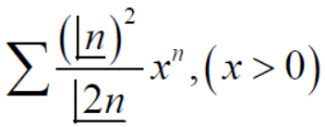
So that,
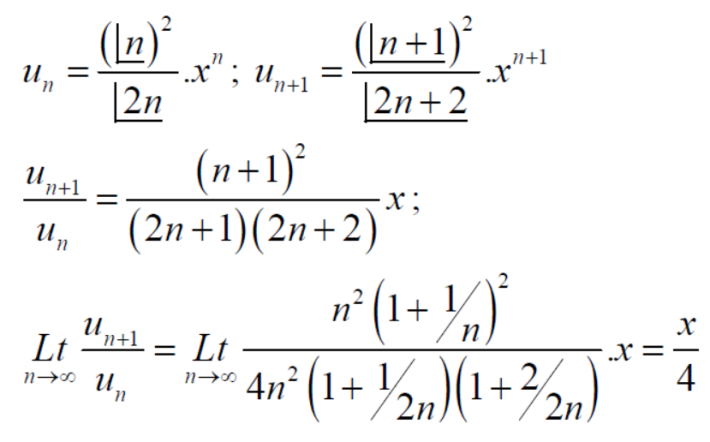
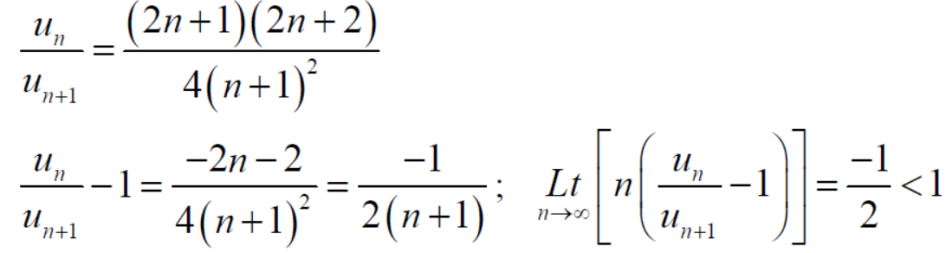
By ratio test 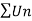 converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the the test fails,
converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the the test fails,
Then ,
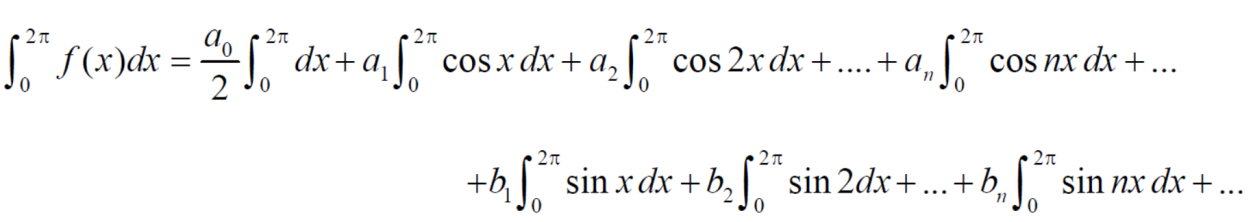
By Raabes’s test  converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
Example-2: Test the convergence of the series,
Sol. As we will neglect the first term, we get
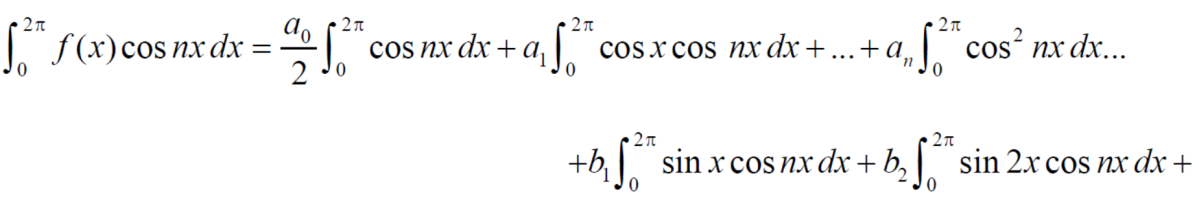
By ration test 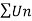 is convergent when x<1 and divergent when x>1, when x= 1,
is convergent when x<1 and divergent when x>1, when x= 1,
The rario test fails, then

By Rabee’s test 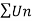 is convergent , hence the given series is convergent when x≤ 1 and divergent If x >1.
is convergent , hence the given series is convergent when x≤ 1 and divergent If x >1.
Example-3: Test the nature of the following series:
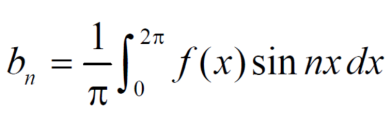
Sol.
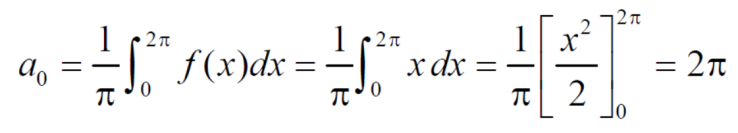
By ration test  is convergent when (x/4)<1 and divergent when x>4, when x= 4,
is convergent when (x/4)<1 and divergent when x>4, when x= 4,
The ratio test fails, then
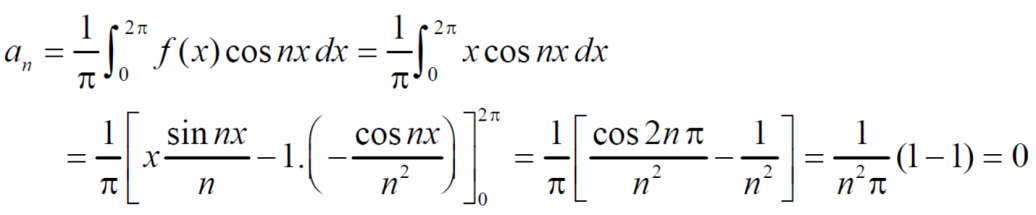
By Rabee’s test 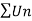 is convergent , hence the given series is convergent when x<4 and divergent If x >=4.
is convergent , hence the given series is convergent when x<4 and divergent If x >=4.
Key takeaways-
1. If 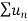 is a series of positive terms such that
is a series of positive terms such that 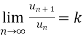 then,
then,
1. if k<1 , the series will be convergent.
2. if k>1 , then the series will be divergent.
A series of the form,
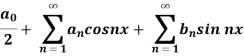
Is called fourier series , where
 are constants.
are constants.
Any periodic function can be expanded in the form of fourier series.
Determination of  ,
, 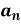 ,
, 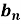 of Fourier series-
of Fourier series-
We know that, the fourier series,
f(x) = 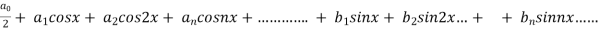 ------------ eq.(1)
------------ eq.(1)
To find 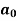 –
–
Intergrate equation (1) on both sides, from 0 to 2π
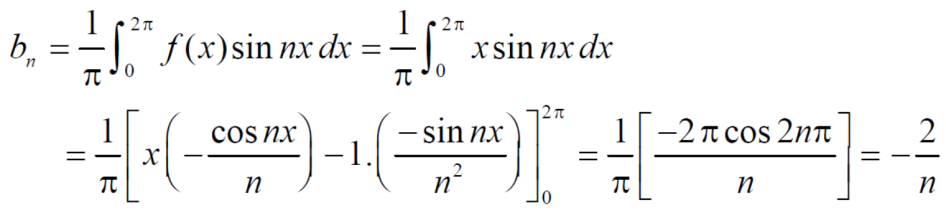
Which gives,
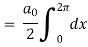
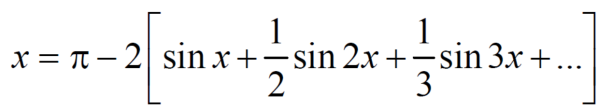
To find 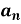 -
-
Multiply each side of eq. (1) by cosnx and integrate from 0 to 2π
We get,
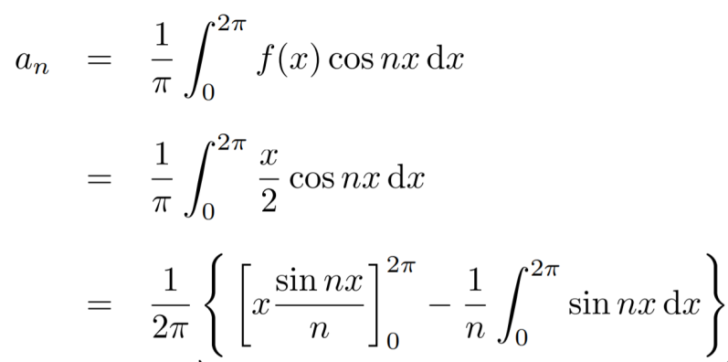
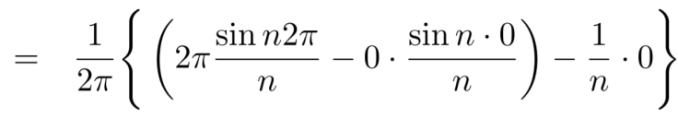
Similarly we can find 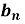 by, multiplying eq. (1) by sin nx and integrating from 0 to 2π
by, multiplying eq. (1) by sin nx and integrating from 0 to 2π
Euler’s Formulae-
Euler’s formulae can be defined as-
The Fourier series for the function f(x) in the interval 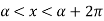 is given by-
is given by-
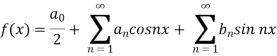
Here-
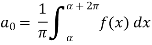
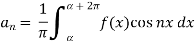
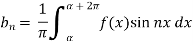
Where-
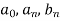 are called Euler’s formulae.
are called Euler’s formulae.
Example: Find the fourier series of the function f(x) = x where 0 < x < 2 π
Sol. We know that, from fourier series,
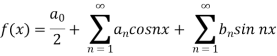
first we will find 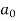 ,
,
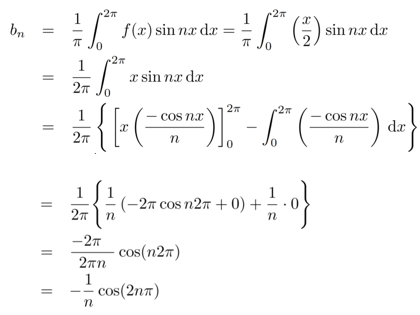
Now, 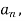
And 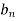 ,
,
Put these value in fourier series, we get
Example: Find the Fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
Sol. First we will find
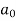 =
= 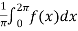
= 
=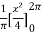
= π
 = π
= π
Similarly,

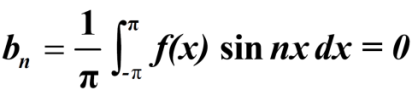
Which gives, 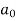 = 0
= 0
Now,
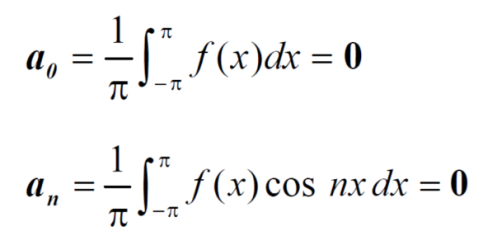
We get, 
We know that, the fourier series
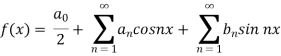
Put these values in fourier series, we get
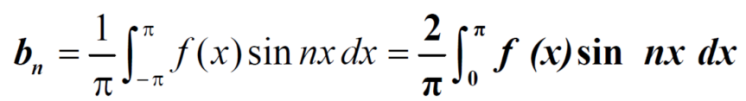
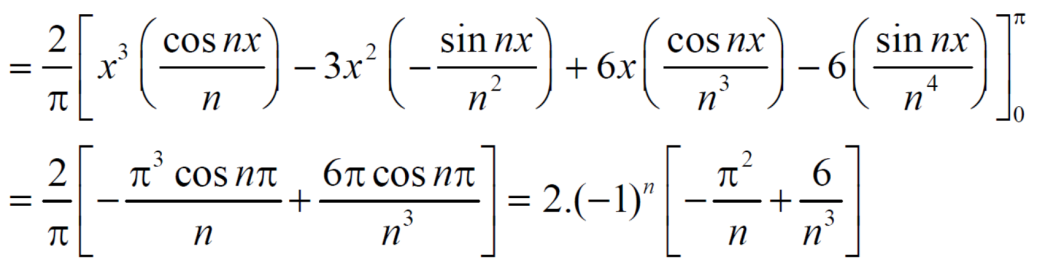
Example: Find the Fourier series for f(x) = 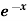 in the interval
in the interval  .
.
Sol.
Suppose
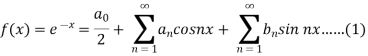
Then-
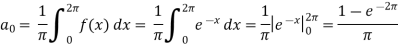
And

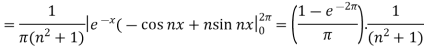
So that-
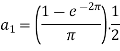
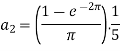
And then-

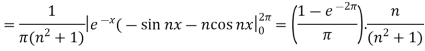

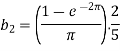
Now put these value in equations (1), we get-
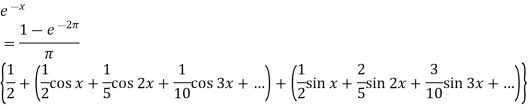
Fourier series of even and odd function
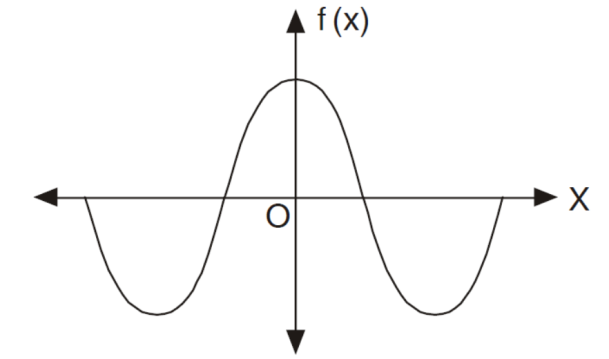
Odd function-
A function f(x), which is written as ,
f( - x ) = - f(x)
is known as odd function.
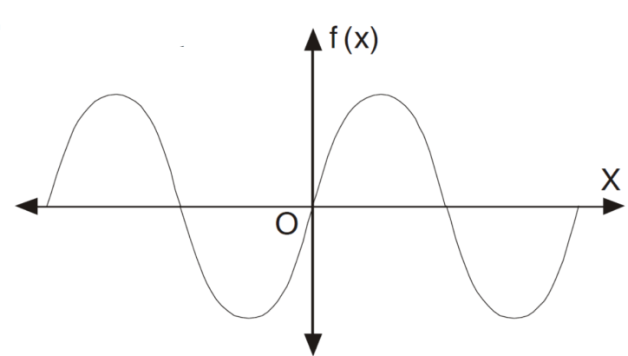
The graph of the odd function looks like-
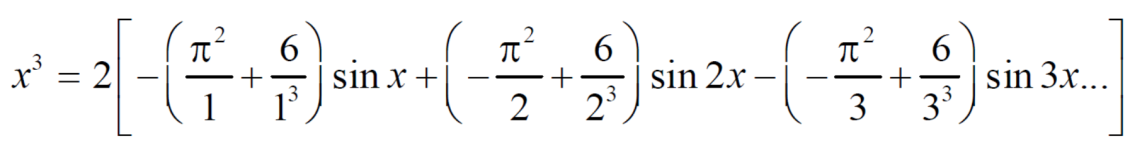
The graph of the function is symmetric about x-axis.
And the area under the curve from -π to π is always zero.(see fig)
Even function-
If f(-x) = f(x) then the function is known as even function.
The graph of the function f(x) looks like-
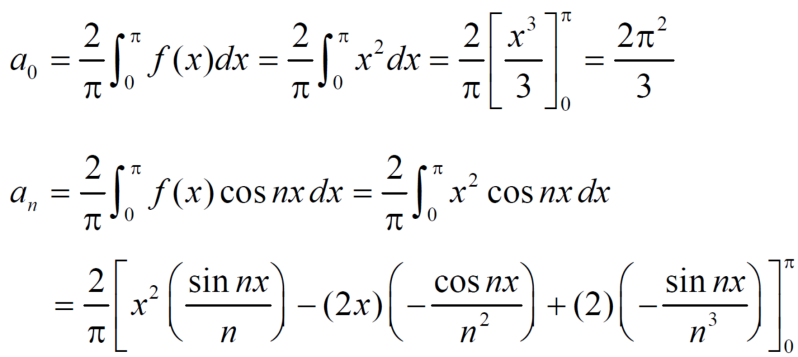
Area under the curve from -π to π will always be double the area from 0 to π
Expansion of an even function-
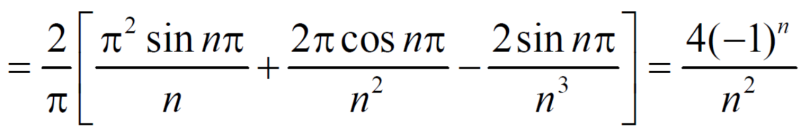
Here cos nx and f(x) are both even functions.
As we know that the product of two even numbers will be even.
Such as product of f(x) and cosnx will always be even.
Now,
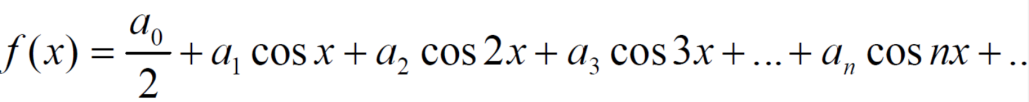
Here we see that sin nx is an odd function.
So that we do not need to find 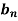
That means the series of an even function contains cosine terms only.
Expansion of an odd function-
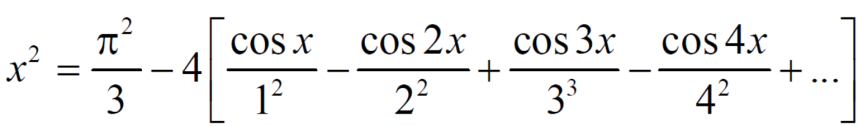
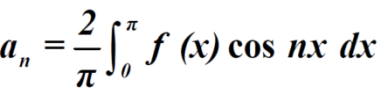
The series of the odd function contains only sine terms.
Example: Find the Fourier expression of f(x) = x³ for –π< x <π.
Sol.
Here, we can see that f(x) Is an odd function
So that,
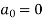 and
and 

We will use here ,

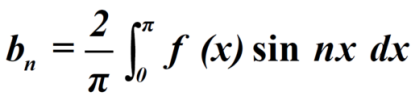
We get the value of f(x),
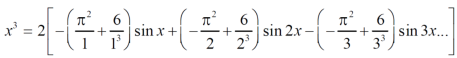
Example: Find the Fourier series expansion of the periodic function of period 2π.
f(x) = x² , -π≤x≤π
Sol. The given function is even, so that,
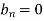
We will find 
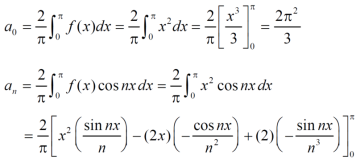
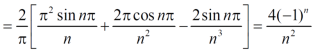
The Fourier series will be,
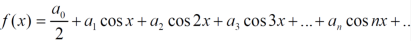
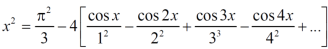
The function is defined in the interval (0,π) and it is immaterial whatever the function may be outside the interval (0,π) to get the series of cosines only we suppose that f(x) is an even function in the interval (-π,π)
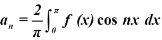
And bn = 0
To expand the as a sine series in the same interval and as an odd function.
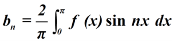
bn = 0.
Example- Find a Fourier series for
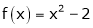 ;
; 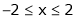
Solution:
Here
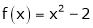 ;
; 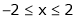
Since f(x) is even function hence 
 It’s Fourier series is
It’s Fourier series is
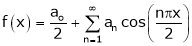 … (1)
… (1)
Where
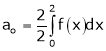
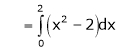
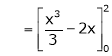

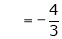
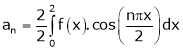
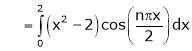
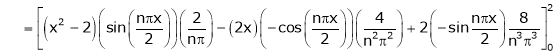
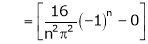
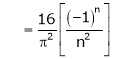
Hence equation (1) becomes,
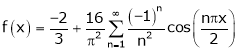
Example: Find half range cosine series of  in the interval
in the interval  and hence deduce that
and hence deduce that
a) 
b) 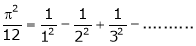
Solution:
Here
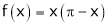 ;
; 
Hence it’s half range cosine series is,
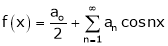 … (1)
… (1)
Where
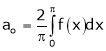
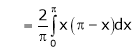
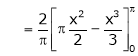
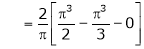

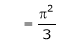
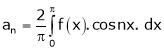
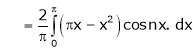
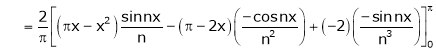
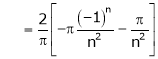
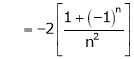
Hence equation (1) becomes,
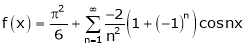
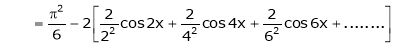
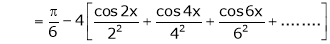 … (2)
… (2)
Put x = 0, we get
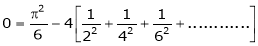
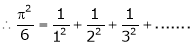
Hence the result
Put 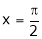 we get,
we get,
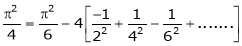
i.e. 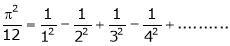
Example: Find the Fourier sine series for the function-

Where ‘a’ is a constant.
Sol. here we know-
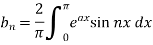
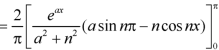
We know that-
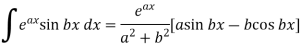
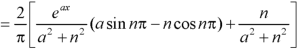
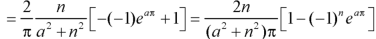
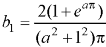
And
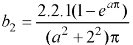
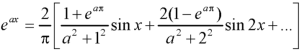
Key takeaways-
Then t is called the periodic of the function f(x).
2. A series of the form,

Is called fourier series , where
 are constants.
are constants.
3. 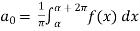
4. 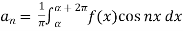
5. 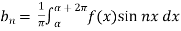
6. A function f(x), which is written as ,
f( - x ) = - f(x)
is known as odd function.
7. If f(-x) = f(x) then the function is known as even function.
8. Expansion of an even function-
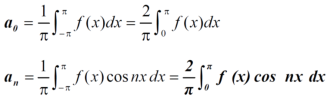
9. Expansion of an odd function-
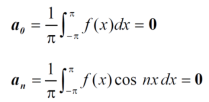
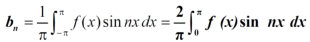
References