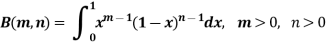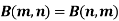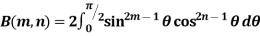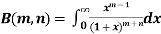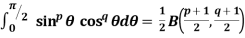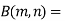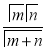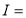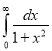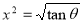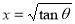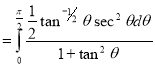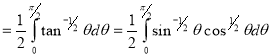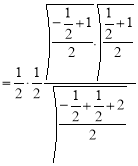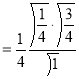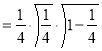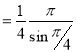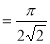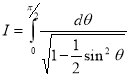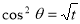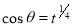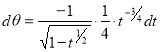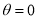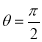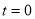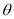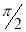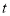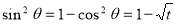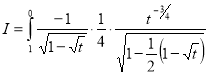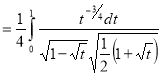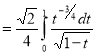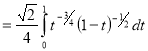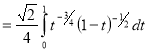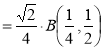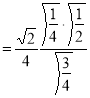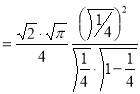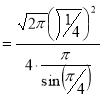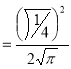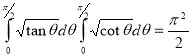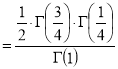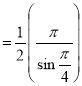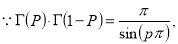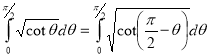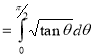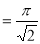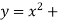Unit-2
Multivariable Calculus-II
Definite integrals-
When we apply limits in indefinite integrals are called definite integrals.
If an expression is written as 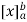 , here ‘b’ is called upper limit and ‘a’ is called lower limit.
, here ‘b’ is called upper limit and ‘a’ is called lower limit.
If f is an increasing or decreasing function on interval [a , b], then
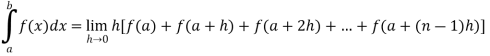
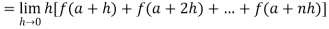
Where 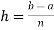
Properties-
1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-
If a = b, then
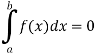
And if a>b, then
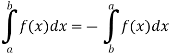
2. Integral of a constant function-

3. Constant multiple property-
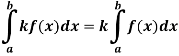
4. Interval union property-
If a < c < b, then
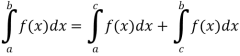
5. Inequality-
If c and d are constants such that  for all x in [a , b], then
for all x in [a , b], then
c(b – a)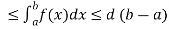
Note- if a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.
Example-1: Evaluate .
.
Sol. Here we notice that f:x→cos x is a decreasing function on [a , b],
Therefore by the definition of the definite integrals-
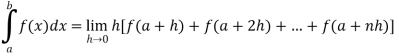
Then
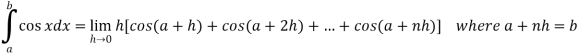
Now,
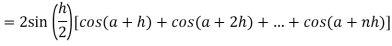
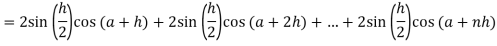
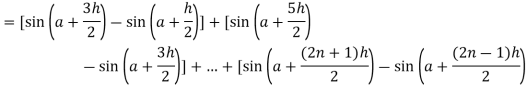
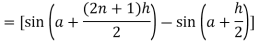
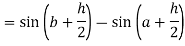
Here 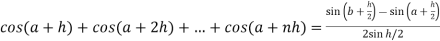
Thus
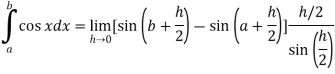
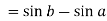
Example-2: Evaluate 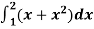
Sol. Here 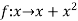 is an increasing function on [1 , 2]
is an increasing function on [1 , 2]
So that,
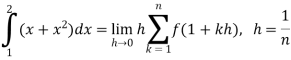


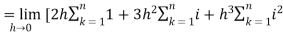 …. (1)
…. (1)
We know that-
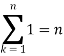
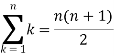
And
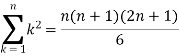
Then equation (1) becomes-
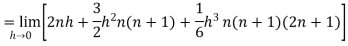
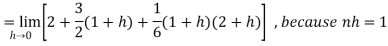
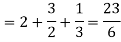
Note- we can find the definite integral directly as-
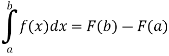
Example-3: Evaluate- 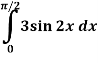 Sol.
Sol. 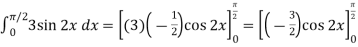
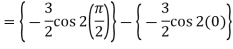
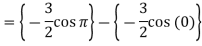
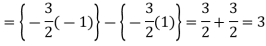
Improper integrals of first kind-
When one or both limits of integration are infinite then this is called improper integral.
Improper integrals
(1) Let f is function defined on [a, ∞) and it is integrable on [a , t] for all t >a, then
If 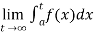 exists, then we define the improper integral of f over [a, ∞) as follows-
exists, then we define the improper integral of f over [a, ∞) as follows-
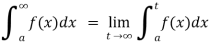
(2) Let f is function defined on (-∞,b] and it is integrable on [t , b] for all t >b, then
If 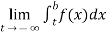 exists, then we define the improper integral of f over (-∞ , b] as follows-
exists, then we define the improper integral of f over (-∞ , b] as follows-
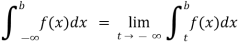
(3) Let f is function defined on (-∞, ∞] and it is integrable on [a , b] for every closed and bounded interval [a , b] which is the subset of R., then
If  and
and 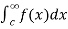 exist for some c belongs to R , then we define the improper integral of f over (-∞ ,∞ ) as follows-
exist for some c belongs to R , then we define the improper integral of f over (-∞ ,∞ ) as follows-
 =
= 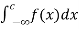 +
+ 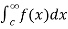
(4) Let f is function defined on (a ,∞) and 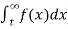 exists for all t>a , then
exists for all t>a , then
If 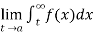 exists , then we define the improper integral of f over (a , ∞) as follows-
exists , then we define the improper integral of f over (a , ∞) as follows-
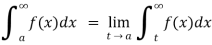
(5) Let f is function defined on (-∞ , b) and 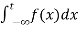 exists for all t<b , then
exists for all t<b , then
If 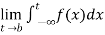 exists , then we define the improper integral of f over (-∞ , b) as follows-
exists , then we define the improper integral of f over (-∞ , b) as follows-
Note-
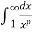
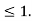
Improper integrals over finite intervals-
(1) Let f is function defined on (a, b] and  exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If 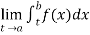 exists , then we define the improper integral of f over (a , b] as follows-
exists , then we define the improper integral of f over (a , b] as follows-
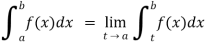
(2) Let f is function defined on [a, b) and 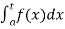 exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If 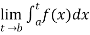 exists, then we define the improper integral of f over [a , b) as follows-
exists, then we define the improper integral of f over [a , b) as follows-
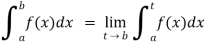
(3) Let f is function defined on [a, c) and (c , b] . if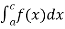 and
and  exist then we define the improper integral of f over [a , b] as follows-
exist then we define the improper integral of f over [a , b] as follows-
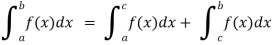
We will read more about the uses of improper integrals in the next topic.
Convergence and divergence of the integrals-
As we have read about improper integrals, we will understand how to check the convergence and divergence of the integrals.
Rules for convergence/ divergence
(1) If the limit exists and a finite number then the integral is said to be convergent.
(2) If the limit does not exists then the integral is said to be divergent.
Improper integrals of second kind-
When the limits of integration are finite but the integrand is not defined at point between a and b.
Let f(x) 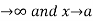 then the integral has a singularity at the lower limit ‘a’.
then the integral has a singularity at the lower limit ‘a’.
Then this singularity is cut off by letting-
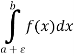
Where 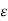 is a very small positive number.
is a very small positive number.
For a convergent improper integral o second kind-

Which ignores the contribution of singularity.
Example-1: Find out the integral 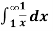 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Here we will convert the integral into limit ,
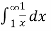 =
= 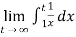
= 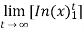
= 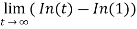
= ∞
As we can see , here limit does not exist. i.e. that is infinity.
So we can say that the given integral is divergent.
Example-2: find out the integral 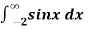 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Covert to the limit ,
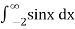 =
= 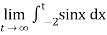
= 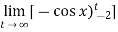
= 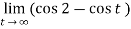
Again the limit does not exist that means the integral is divergent.
Example-3: Find out the integral 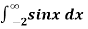 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. Follow the same process as we did above,
Here limit exists and finite , so that the integral is convergent. And its value is 2√3.
Example-4: Find out the integral is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
Sol. As we see, the given is integrand is not continuous at x = 0 , we will split the integral,
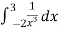 =
= 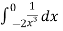 +
+ 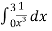
We will check one by one whether the integrals are convergent or divergent,
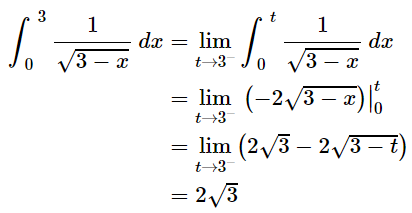
as we found that, integral is divergent
we don’t need to check for the second one.
Example-5: Test for convergence or divergence of the following improper integral-
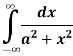
Sol. This is a improper integral of first kind and limits are infinite,
Now
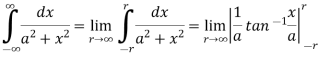
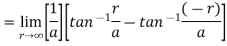
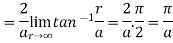
Integral convergent.
Key takeaways-

Where 
2. if a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.
3. Let f is function defined on [a, ∞) and it is integrable on [a , t] for all t >a, then
4. If 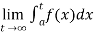 exists, then we define the improper integral of f over [a, ∞) as follows-
exists, then we define the improper integral of f over [a, ∞) as follows-
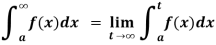
The beta and gamma functions are defined as-
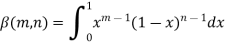
And

These integrals are also known as first and second Eulerian integrals.
Note- Beta function is symmetrical with respect to m and n.
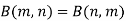
Some important results-
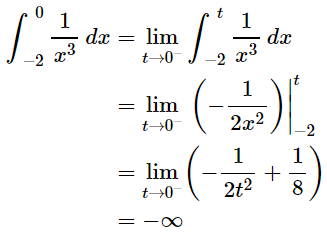
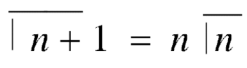

Ex.1: Evaluate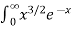 dx
dx
Solution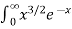 dx =
dx = 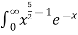 dx
dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2. ½ γ(½ )
= 3/2. ½ π
= ¾ π
Ex. 2: Find γ(-½)
Solution: (-½) + 1= ½
γ(-1/2) = γ(-½ + 1) / (-½)
= - 2 γ(1/2 )
= - 2 π
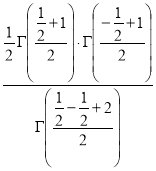
Ex3. Show that 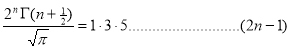

Solution:
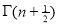 =
= 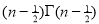
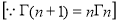
= 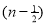
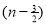
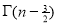
= 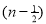
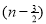
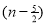
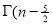 ) .......................
) .......................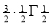
= 
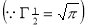
= 
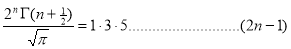
Ex. 4: Evaluate 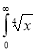
 dx.
dx.
Solution: Let 
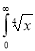
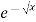 dx
dx
Put  or
or 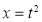 ;dx
;dx
=2t dt .
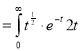 dt
dt
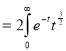 dt
dt
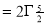
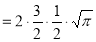
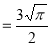
Ex. 5: Evaluate 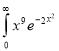 dx.
dx.
Solution: Let 
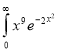 dx.
dx.
x | 0 |
|
t | 0 |
|
Put 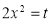 or
or 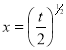 ;
;
4x dx = dt
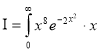 dx
dx

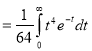
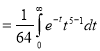
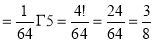
Evaluation of beta function 𝛃 (m, n)-
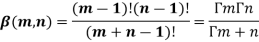
Here we have-
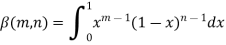
Or

Again integrate by parts, we get-
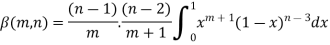
Repeating the process above, integrating by parts we get-
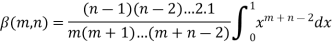
Or
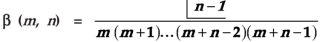
Evaluation of gamma function-
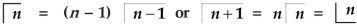

Integrating by parts, we take 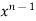 as first function-
as first function-

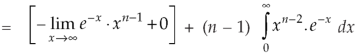
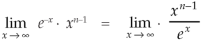
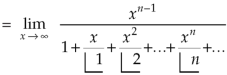
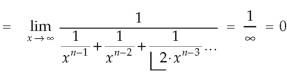
We get-
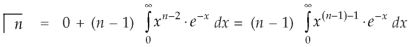

Replace n by n+1,
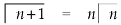
Relation between beta and gamma function-
We know that-
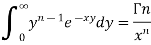
 ………… (1)
………… (1)
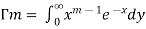 …………………..(2)
…………………..(2)
Multiply equation (1) by 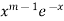 , we get-
, we get-
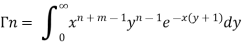
Integrate both sides with respect to x within limits x = 0 to x = 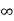 , we get-
, we get-
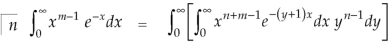
But
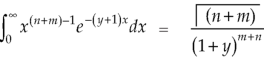
By putting λ = 1 + y and n = m + n
We get by using this result in (2)-
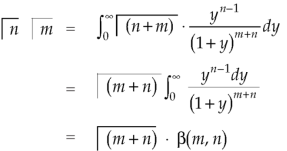
So that-
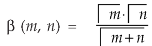
Definition : Beta function
|
Properties of Beta function : |
2. |
3. |
4. |
Example(1): Evaluate

Solution:
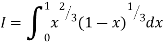
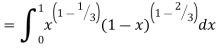
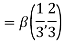

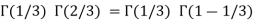
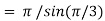
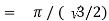
= 2 π/3
Example(2): Evaluate: I = 02 x2 / (2 – x ) . dx
Solution:
Letting x = 2y, we get
I = (8/2) 01 y2 (1 – y ) -1/2dy
= (8/2). B (3, 1/2 )
= 642 /15
BETA FUNCTION MORE PROBLEMS
Relation between Beta and Gamma functions :
| ||||||
Example(1): Evaluate: I = 0a x4 (a2 – x2 ) . dx Solution: Letting x2 = a2 y , we get I = (a6 / 2) 01 y 3/2 (1 – y )1/2dy = (a6 / 2) . B(5/2 , 3/2 ) = a6 /3 2
Example(2): Evaluate: I = 02 x (8 – x3 ) . dx Solution: Let x3 = 8y I = (8/3) 01 y-1/3 (1 – y ) 1/3 . dy
= (8/3) B(2/3 , 4/3 ) = 16 π / ( 9 3 )
Example (3): Prove that Solution: Let Put
Example (4): Evaluate Solution: Let Put When
Also
Example (5): Show that Solution: =
|
Key takeaways-
1.The beta and gamma functions are defined as-
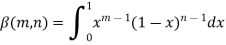
And
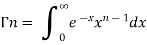
These integrals are also known as first and second Eulerian integrals.
3. Beta function is symmetrical with respect to m and n.
We use Dirichlet’s integral to find triple and double integrals by expressing in beta and gamma function.
We can find plane area, volume of a solid region, centroid by using Dirichlet’s integral.
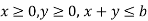
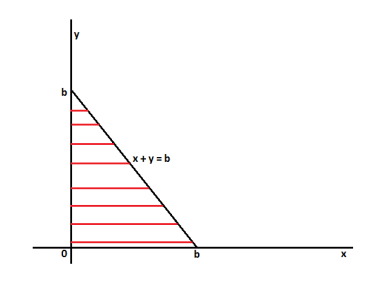
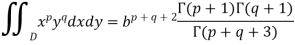
2. Suppose V is the solid region, tetrahedron in the first octant, bounded by the plane x + y + z = 0. Then the triple integral over V-

Example: Find the area contained in the first quadrant enclosed by the curve 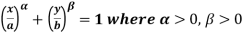 given that density at any point p(x, y) is k
given that density at any point p(x, y) is k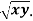
Sol. The area A of the plane region is-
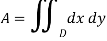
Now put 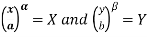 then x =
then x = 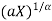 and
and  then-
then-
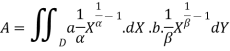
Where 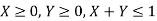 , So that-
, So that-
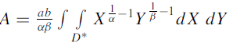
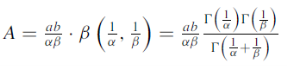
Dirichlet’s theorem for three variables-
Suppose l, m, n are positive, then the triple integral-

Where V is the region 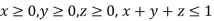
Example: Find the mass of an octant of the ellipsoid 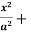
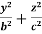 , the density at any point being p = kxyz
, the density at any point being p = kxyz
Sol.
As we know that-

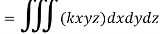
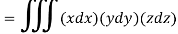
Put 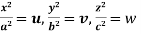 and u+v +w = 1
and u+v +w = 1
Therefore-
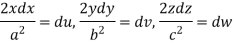
Then mass-


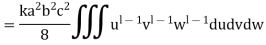
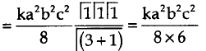
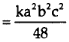
Key takeaways-
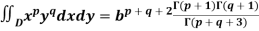
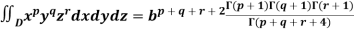
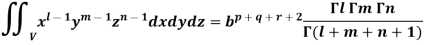
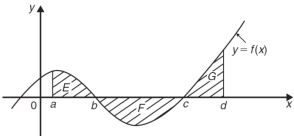
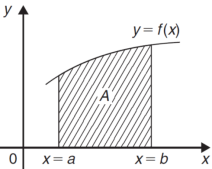
Area under and between the curves-
Total shaded area will be as follows of the given figure (by using definite integrals)-
Total shaded area = 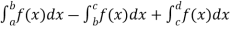
Example-1: Determine the area enclosed by the curves-
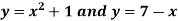
Sol. We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-
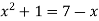
Which gives-
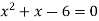
By factorization,
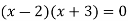
Which means,
x = 2 and x = -3
By determining the intersection points the range the values of x has been found-
x | -3 | -2 | -1 | 0 | 1 | 2 |
| 10 | 5 | 2 | 1 | 2 | 5 |
And
x | -3 | 0 | 2 |
y = 7 - x | 10 | 7 | 5 |
We get the following figure by using above two tables-
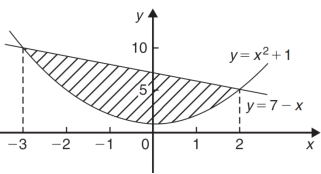
Area of shaded region = 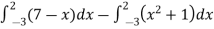

= 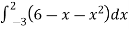
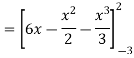
= ( 12 – 2 – 8/3 ) – (-18 – 9/2 + 9)
= 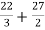
= 125/6 square unit
Example-2: Determine the area bounded by three straight lines y = 4 – x, y = 3x and 3y = x
Sol. We get the following figure by using the equations of three straight lines-
y = 4 – x, y = 3x and 3y = x
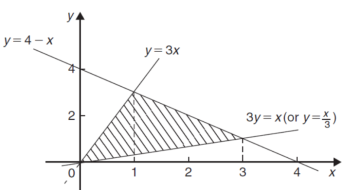
Area of shaded region-

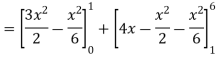
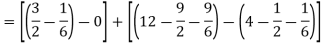

Example-3: Find the area enclosed by the two functions-
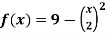 and g(x) = 6 – x
and g(x) = 6 – x
Sol. We get the following figure by using these two equations
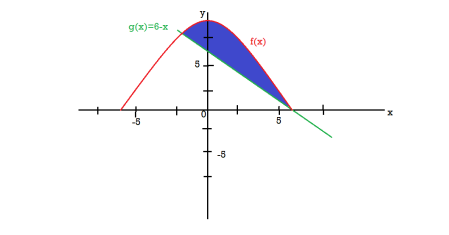
To find the intersection points of two functions f(x) and g(x)-
f(x) = g(x)

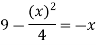
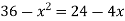
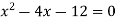
On factorizing, we get-
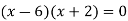
x = 6, -2
Now
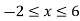
Then, area under the curve-
A = 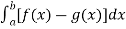
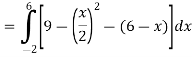
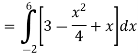
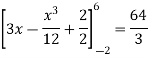
Therefore the area under the curve is 64/3 square unit.
Areas and volumes of revolutions-
The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-
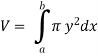
Suppose the curve x = f(y) is rotated  about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
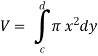
Example-1: Find the area enclosed by the curves 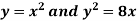 and if the area is rotated
and if the area is rotated  about the x-axis then determine the volume of the solid of revolution.
about the x-axis then determine the volume of the solid of revolution.
Sol. We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
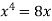
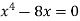
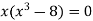
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
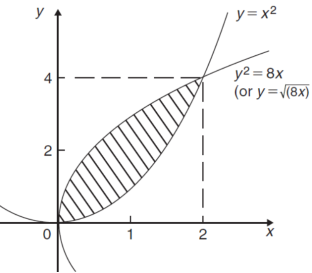
Then,
The area of the shaded region will be-
A = 
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving 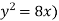 – (volume produced by revolving
– (volume produced by revolving 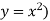
= 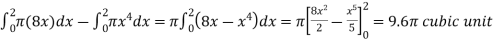
Method of cylindrical shells-
Let f(x) be a continuous and positive function. Define R as the region bounded above by the graph f(x), below by the x-axis, on the left by the line x = a and on the right x = b, then the volume of the solid of revolution formed by revolving R around the y-axis is given by
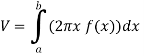
Example-2: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].
Sol. The graph of the function f(x) = 1/x will look like-
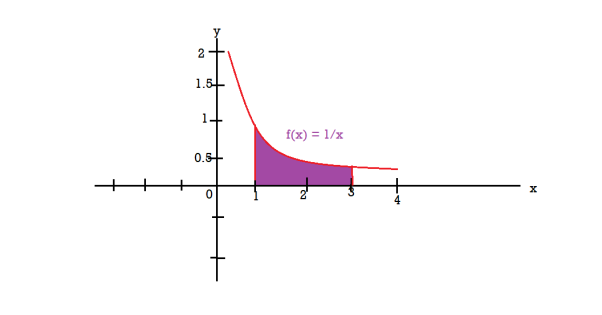
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]
Then the volume of the solid will be-
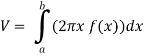
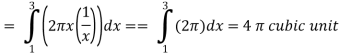
Example-3: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].
Sol. The graph of the function f(x) = 2x - x² will be-
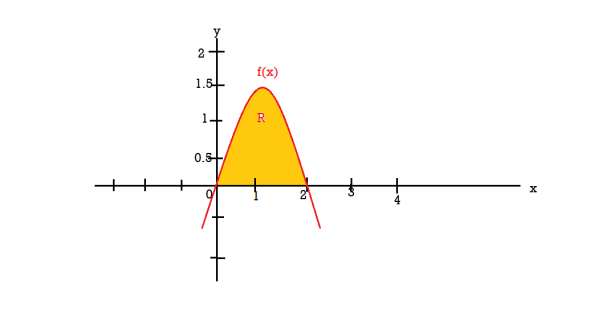
The volume of the solid is given by-
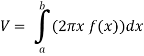

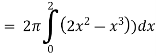
= 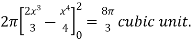
Key takeaways-
The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-
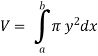
2. Method of cylindrical shells-
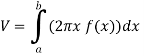
References