Unit - 2
Projections of Planes
Parallel projection is obtained by assuming the observer at infinite distance from the 3 objects. Hence, the visual rays are considered as parallel to one another. These lines of sight are used to project the object on a standard plane. The object is projected to a plane by drawing straight lines from each and every point on the object. These lines used for projecting the object are ‘projectors. The plane to which the object is projected is the ‘plane of projection’. All projectors are parallel to one another and perpendicular to the plane of projection. The image or view obtained on the plane is the ‘projection’.
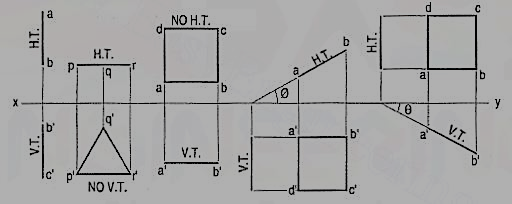
A square ABCD is perpendicular to the H.P. and inclined at an angle φ to the V.P. Its V.T. is perpendicular to xy. Its H.T. is inclined at φ to xy.
Its top view ab is a line inclined at φ to xy. The front view a'b'c'd' is smaller than ABCD.
(b) Plane, perpendicular to the V.P. and inclined to the H.P.
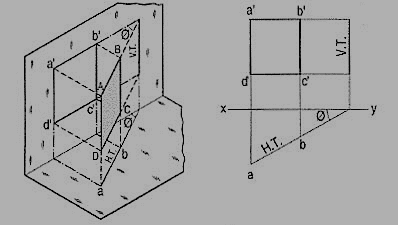
A square ABCD is perpendicular to the V.P. and inclined at an angle θ to the H.P. Its H.T. is perpendicular to xy. Its V.T. makes the angle e with xy. Its front view a'b' is a line inclined at θ to xy. The top view abed is a rectangle which is smaller than the square ABCD.
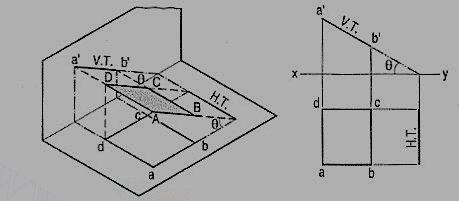
Fig. shows the projections and the traces of all these perpendicular planes by third-angle projection method.
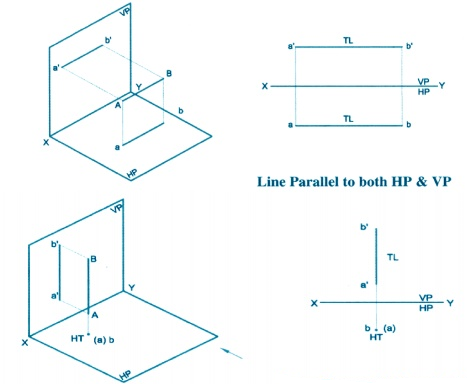
(a) A line AB (fig. 10-9) is inclined at e to the H.P. and is parallel to the V.P.
The end A is in the H.P. AB is shown as the hypotenuse of a right-angled
triangle, making the angle e with the base.
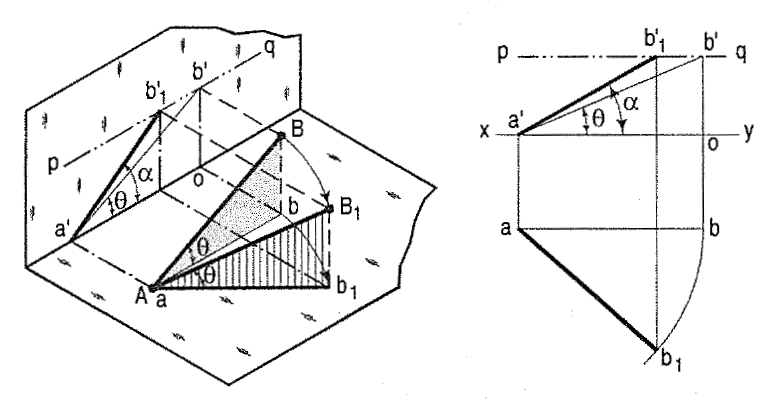
The top view ab is shorter than AB and parallel to xy. The front view a'b'
is equal to AB and makes the angle 0 with xy.
Keeping the end, A fixed and the angle 0 with the H.P. constant, if the
end B is moved to any position, say 81, the line becomes inclined to the
V.P. also.
In the top view, b will move along an arc, drawn with a as centre and
ab as radius, to a position b1. The new top view ab1 is equal to ab but
shorter than AB.
In the front view, b' will move to a point b'1 keeping its distance from xy
constant and equal to b'o; i.e., it will move along the line pq, drawn
through b' and parallel to xy. This line pq is the locus or path of the end
8 in the front view. b'1 will lie on the projector through b1• The new front
view a'b'1 is shorter than a'b' (i.e., AB) and makes an angle α with xy. α
is greater than 0.
Thus, it can be seen that as long as the inclination 0 of AB with the H.P.
is constant, even when it is inclined to the V.P.
(i) its length in the top view, viz. ab remains constant; and
(ii) the distance between the paths of its ends in the front view,
viz. b'o remains constant.
(b) The same line AB (fig. 10-10) is inclined at 0 to the V.P. and is parallel
to the H.P. Its end A is in the V.P. AB is shown as the hypotenuse of a
right-angled triangle making the angle 0 with the base.
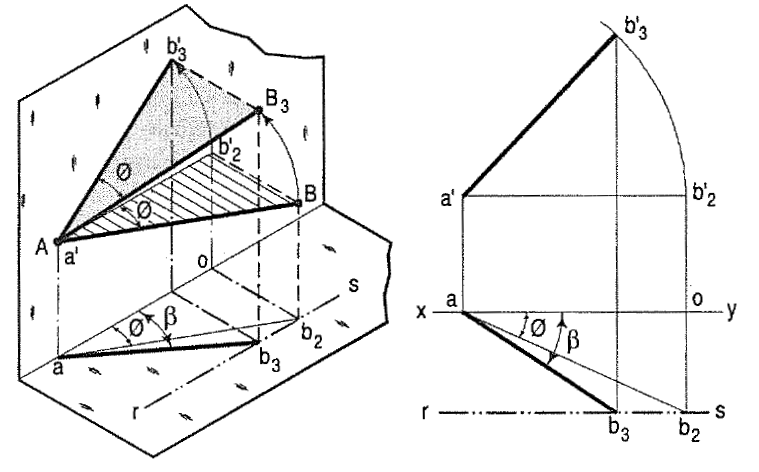
The front view a'b'2 is shorter than AB and parallel to xy. The top view
ab2 is equal to AB and makes an angle 0 with xy.
Keeping the end, A fixed and the angle 0 with the V.P. constant, if B is
moved to any position, say B3, the line will become inclined to the H.P. also.
In the front view, b'2, will move along the arc, drawn with a' as centre
and a'b'2 as radius, to a position b' 3• The new front view a'b'3 is equal to
a'b'2 but is shorter than AB.
In the top view, b2 will move to a point b3 along the line rs, drawn
through b2 and parallel to xy, thus keeping its distance from the path of
a, viz. b2o constant. rs is the locus or path of the end B in the top view.
The point b3 lies on the projector through b'3. The new top view ab3 is
shorter than ab2 (i.e., AB) and makes an angle β with xy. β is greater than 0.
Here also we find that, as long as the inclination of AB with the V.P.
does not change, even when it becomes inclined to the H.P.
(i) its length in the front view, viz. a'b'2 remains constant; and
(ii) the distance between the paths of its ends in the top view, viz.
b2o remains constant.
Hence, when a line is inclined to both the planes, its projections are shorter
than the two length and inclined to xy at angles greater than the true inclinations.
These angles viz. α and β are called apparent angles of inclination.
A solid has three dimensions, viz. length, breadth and thickness. To represent a
solid on a flat surface having only length and breadth, at least two orthographic
views are necessary. Sometimes, additional views projected on auxiliary planes become necessary to make the description of a solid complete.
Solids may be divided into two main groups:
(1) Polyhedra.
(2) Solids of revolution.
Polyhedra: A polyhedron is defined as a solid bounded by planes called faces.
When all faces are equal and regular, the polyhedron is said to be regular.
There are seven regular polyhedra which may be defined as stated below:
A solid in simple position may have its axis perpendicular to one reference plane
or parallel to both. When the axis is perpendicular to one reference plane, it is
parallel to the other. Also, when the axis of a solid is perpendicular to a plane,
its base will be parallel to that plane. We have already seen that when a plane is
parallel to a reference plane, its projection on that plane shows its true shape and size.
Therefore, the projection of a solid on the plane to which its axis is perpendicular,
will show the true shape and size of its base.
Hence, when the axis is perpendicular to the ground, i.e. to the H.P., the top view
should be drawn first and the front view projected from it.
When the axis is perpendicular to the V.P., beginning should be made with the
front view. The top view should then be projected from it.
When the axis is parallel to both the H.P. and the V.P., neither the top view nor
the front view will show the actual shape of the base. In this case, the projection
of the solid on an auxiliary plane perpendicular to both the planes, viz. the side view must be drawn first. The front view and the top view are then projected from the side view. The projections in such cases may also be drawn in two stages.
(fig. 13-12): Draw the projections of a triangular prism, base40 mm side and axis 50 mm long, resting on one of its bases on the H.P. with a vertical face perpendicular to the V.P.
Axis perpendicular to HP
(i) As the axis is perpendicular to the ground i.e., the H.P. begin with the top view. It will be an equilateral triangle of sides 40 mm long, with one of its
sides perpendicular to xy. Name the corners as shown, thus completing
the top view. The corners d, e and fare hidden and coincide with the top
corners a, b and c respectively.
(ii) Project the front view, which will be a rectangle. Name the corners. The line
b'e' coincides with a'd'.
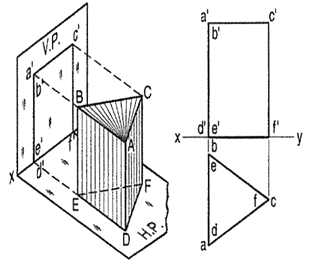
Axis Parallel to Both Reference Planes
A triangular prism1 base 40 mm side and height 65 mm is resting on the H.P. on one of its rectangular faces with the axis parallel to the V.P. Draw its projections.
As the axis is parallel to both the planes, begin with the side view. (i) Draw an equilateral triangle representing the side view, with one side in xy.
(ii) Project the front view horizontally from this triangle.
(iii) Project down the top view from the front view and the side view, as shown. 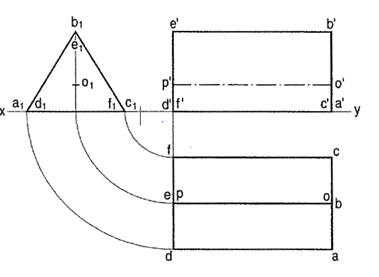
Axis parallel to one Reference Plane and inclined to the other Reference Plane
When a solid has its axis inclined to one plane and parallel to the other, its
projections are drawn in two stages.
(1) In the initial stage, the solid is assumed to be in simple position, i.e., its
axis perpendicular to one of the planes.
If the axis is to be inclined to the ground, i.e., the H.P., it is assumed to be perpendicular to the H.P. in the initial stage. Similarly, if the axis is to
be inclined to the V.P., it is kept perpendicular to the V.P. in the initial stage
(i) if the solid has an edge of its base parallel to the H.P. or in the H.P. or on the ground, that edge should be kept perpendicular to the V.P.; if the edge of the base is parallel to the V.P. or in the V.P., it should be kept perpendicular to the H.P.
(ii) If the solid has a corner of its base in the H.P. or on the ground, the sides of the base containing that corner should be kept equally inclined to the V.P.; if the corner is in the V.P., they should be kept equally inclined to the H.P.
(2) Having drawn the projections of the solid in its simple position, the final
projections may be obtained by one of the following two methods:
(i) Alteration of position: The position of one of the views is altered as required and the other view projected from it.
(ii) Alteration of reference line: A new reference line is
drawn according to the required conditions, to represent an auxiliary plane and the final view projected on it.
In the first method, the reproduction of a view accurately in the altered position
is likely to take considerable time, specially, when the solid has curved surfaces or too many edges and corners. In such cases, it is easier and more convenient to
adopt the second method. Sufficient care must however be taken in transferring the distances of various points from their respective reference lines.
After determining the positions of all the points for the corners in the final view, difficulty is often felt in completing the view correctly. The following sequence for
joining the corners may be adopted:
(a) Draw the lines for the edges of the visible base. The base, which (compared
to the other base) is further away from xy in one view, will be fully visible in
the other view.
(b) Draw the lines for the longer edges. The lines which pass through the figure
of the visible base should be dashed lines.
(c) Draw the lines for the edges of the other base.
It should always be remembered that, when two lines representing the edges
cross each other, one of them must be hidden and should therefore be drawn as
a dashed line.
These are illustrated according to the position of the section plane with reference
to the principal planes as follows:
(1) Section plane parallel to the V.P.
(2) Section plane parallel to the H.P.
(3) Section plane perpendicular to the H.P. and inclined to the V.P.
(4) Section plane perpendicular to the V.P. and inclined to the H.P.
Section parallel to the VP
Problem 1:
A cube of 35 mm long edges is resting on the H.P. on one of its faces with a vertical face inclined at 30° to the V.P. It is cut by a section plane parallel to the V.P. and 9 mm away from the axis and further away from the V.P. Draw its sectional front view and the top view.
In fig. (i), the section plane is assumed to be transparent and the cube is shown with the cut-portion removed. Four edges of the cube are cut and hence, the section is a figure having four sides.
Draw the projections of the whole cube in the required position [fig.(ii)]. As the section plane is parallel to the V.P., it is perpendicular to the H.P.; hence, the section will be a line in the top view coinciding with the H.T. of the section plane.
(i) Draw a line H.T. in the top view (to represent the section plane) parallel to xy and 9 mm from o.
(ii) Name the points at which the edges are cut, viz. ab at 1, be at 2, gf at 3 and fe at 4.
(iii) Project these points on the corresponding edges in the front view and join them in proper order.
As the section plane is parallel to the V.P., figure 1' 2' 3' 4' in the front view, shows the true shape of the section.
Show the views by dark but thin lines, leaving the lines for the cut-portion fainter.
(iv) Draw section lines in the rectangle for the section.
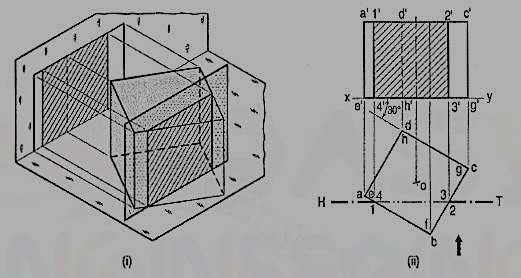
(2) Section plane parallel to the H.P.
Problem 2 A triangular prism, base 30 mm side and axis 50 mm long, is lying on the H.P. on one of its rectangular faces with its axis inclined at 30° to the V.P. It is cut by a horizontal section plane, at 12 mm above the ground. Draw its front view and sectional top view.
As the section plane is horizontal, i.e., parallel to the H.P., it is perpendicular to the V.P. Hence, the section will be a line in the front view, coinciding with the V. T. of the section plane.
(i) Therefore, draw a line V.T. in the front view to represent the section plane, parallel to xy and 12 mm above it.
(ii) Name in correct sequence, points at which the edges are cut viz. a'b' at 1 ', a'c' at 2', d'f' at 3' and d'e' at 4'.
(iii) Project these points on the corresponding lines in the top view and complete the sectional top view by joining them in proper order.
As the section plane is parallel to the H.P., the figure 1 2 3 4 (in the top view) is the true shape of the section.
(3) Section plane perpendicular to the H.P. and inclined to the V.P.
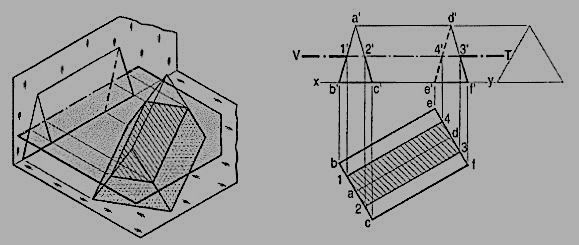
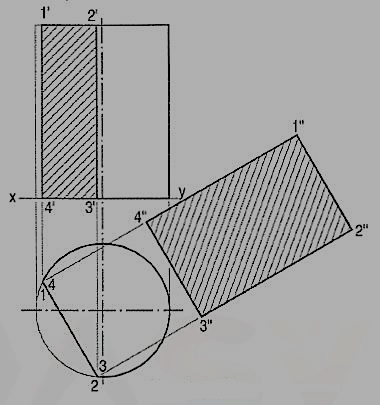
Problem 3.A cube in the same position as in problem 1, is cut by a section plane, inclined at 60° to the V.P. and perpendicular to the H.P., so that the face which makes 60° angle with the V.P. is cut in two equal halves. Draw the sectional front view, top view and true shape of the section.
The section will be a line in the top view coinciding with the H.T. of the section plane.
(i) Draw the projections of the cube. Draw a line H.T. in the top view inclined at 60° to xy and cutting the line ad (or be) at its mid-point.
(ii) Name the corners at which the four edges are cut and project them in the front view. As the section plane is inclined to the V.P., the front view of the section viz. 1' 2' 3' 4' does not reveal its true shape. Only the vertical lines show true lengths, while the true lengths of the horizontal lines are seen in the top view. The true shape of the section will be seen when it is projected on an auxiliary vertical plane, parallel to the section plane.
(iii) Therefore, draw a new reference line x1y1 parallel to the H.T. and project the section on it. The distances of the points from x1y1 should be taken equal to their corresponding distances from xy in the front view. Thus 4" and 3" will be on x1y1. 1" 4" and 2" 3" will be equal to 1' 4' and 2' 3' respectively. Complete the rectangle 1" 2" 3"4" which is the true shape of the section and draw section lines in it.
(4) Section plane perpendicular to the V.P. and inclined to the H.P.
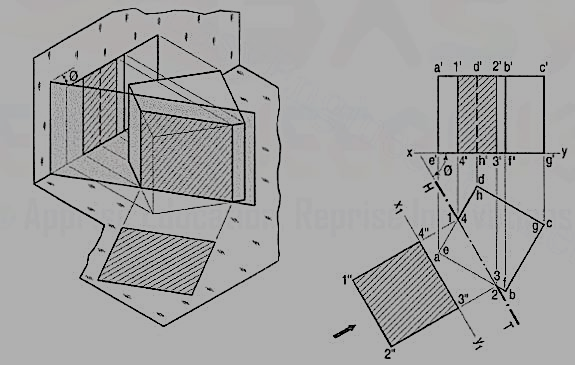
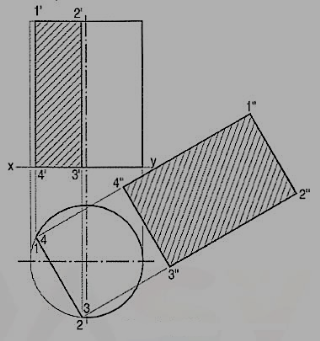
Problem 4. A cube in the same position as in problem 14-1 is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. and passing through the top end of the axis. (i) Draw its front view, sectional top view and true shape of the section. (ii) Project another top view on an auxiliary plane, parallel to the section plane.
The section will be a line in the front view.
(i) Draw a line V.T. in the front view, inclined at 45° to xy and passing through the top end of the axis. It cuts four edges, viz. a' e' at 1 ', a' b' at 2', c'd' at 3' and d'h' at 4'.
(ii) Project the top view of the section, viz. the figure 1 2 3 4. It does not show the true shape of the section, as the section plane is inclined to the H.P. To determine the true shape, an auxiliary top view of the section should be projected on an A.I.P. parallel to the section plane.
(iii) Assuming the new reference line for the A.I.P. to coincide with the V.T., project the true shape of the section as shown by quadrilateral 11 21 31 41. The distances of all the points from the V.T. should be taken equal to their corresponding distances from xy in the top view, e.g. 111' = e'1, 414' = h'4 etc.
(iv) To project an auxiliary sectional top view of the cube, draw a new reference line x1 y1, parallel to the V.T. The whole cube may first be projected and the points for the section may then be projected on the corresponding lines for the edges. Join these points in correct sequence and obtain the required top view.
(v) Draw section lines in the cut-surface, in the views where it is seen. Keep the lines for the removed edges thin and fainter.
Sections of Pyramids
The following cases are discussed in details.
(1) Section plane parallel to the base of the pyramid.
(2) Section plane parallel to the V.P.
(3) Section plane perpendicular to the V.P. and inclined to the H.P.
(4) Section plane perpendicular to the H.P. and inclined to the V.P.
(1) Section plane parallel to the base of the pyramid.
Problem 5: A pentagonal pyramid, base 30 mm side and axis 65 mm long has its base horizontal and an edge of the base parallel to the V.P. A horizontal section plane cuts it at 25 mm above the base. Draw it’s from view and sectional top view.
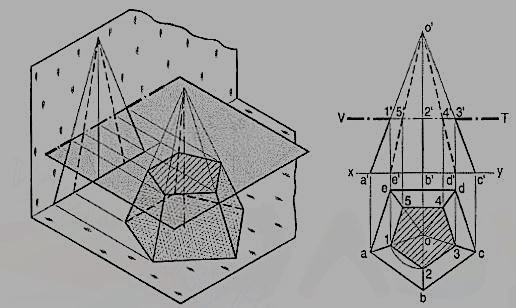
(i) Draw the projections of the pyramid in the required position and show a line V.T. for the section plane, parallel to and 25 mm above the base. All the five slant edges are cut.
(ii) Project the points at which they are cut, on the corresponding edges in the top view. The point 2' cannot be projected directly as the line ob is perpendicular to xy. But it is quite evident from the projections of other points that the lines of the section in the top view, viz. 3-4, 4-5 and 5-1 are parallel to the edges of the base in their respective faces and that the points 1, 3, 4 and 5 are equidistant from o.
(iii) Hence, line 1-2 also will be parallel to ab and o2 will be equal to o1, o3 etc. Therefore, with o as centre and radius o1, draw an arc cutting ob at a point 2 which will be the projection of 2'. Complete the sectional top view in which the true shape of the section, viz. the pentagon 1, 2, 3, 4 and 5 is also seen.
(iv) Hence, when a pyramid is cut by a plane parallel to its base, the true shape of the section will be a figure, like the base; the sides of the section will be parallel to the edges of the base in the respective faces and the corners of the section will be equidistant from the axis.
(2) Section plane parallel to the V.P.
Problem 6 A triangular pyramid, having base 40 mm side and axis 50 mm long, is lying on the H.P. on one of its faces, with the axis parallel to the V.P. A section plane, parallel to the V.P. cuts the pyramid at 6 mm from the axis. Draw its sectional front view and the top view.
(i) Draw the projections of the pyramid in the required position and show a line H.T. (for the cutting plane) in the top view parallel to xy and 6 mm from the axis.
(ii) Project points 1, 2 and 3 (at which the edges are cut) on corresponding edges in the front view and join them. Figure 1' 2' 3' shows the true shape of the section.
(3) Section plane perpendicular to the V.P. and inclined to the H.P.
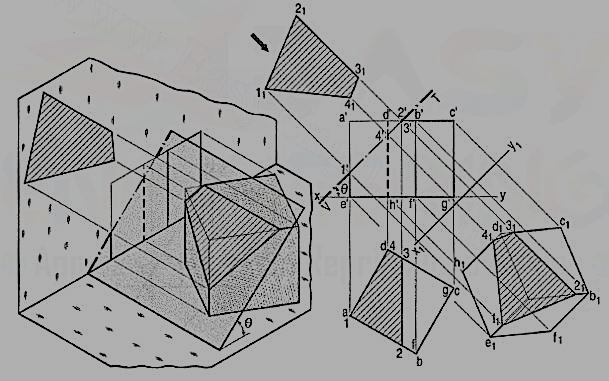
Problem 7 A square pyramid, base 40 mm side and axis 65 mm long, has its base on the H.P. and all the edges of the base equally inclined to the V.P. It is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. and bisecting the axis. Draw its sectional top view, sectional side view and true shape of the section.
(i) Draw the projections of the pyramid in the required position. The section plane will be seen as a line in the front view. Hence, draw a line V.T. through the mid-point of the axis and inclined at 45° to xy. Name in correct sequence the points at which the four edges are cut and project them in the top view. Here also, points 2' and 4' cannot be projected directly.
Hence, assume a horizontal section through 2' and draw a line parallel to the base, cutting o' a' at 2'1. Project 2'1 to 21 on oa in the top view. From 21 draw a line parallel to ab and cutting ob at a point 2. Or, with o as centre and radius o 21, draw an arc cutting ob at 2 and ob at 4. Complete the section 1 2 3 4 by joining the points and draw section lines in it.
(ii) Assuming the V.T. to be the new reference line, draw the true shape of the section. Project the side view from the two views. The removed portion of the pyramid may be shown by thin and faint lines.
(4) Section plane perpendicular to the H.P. and inclined to the V.P.
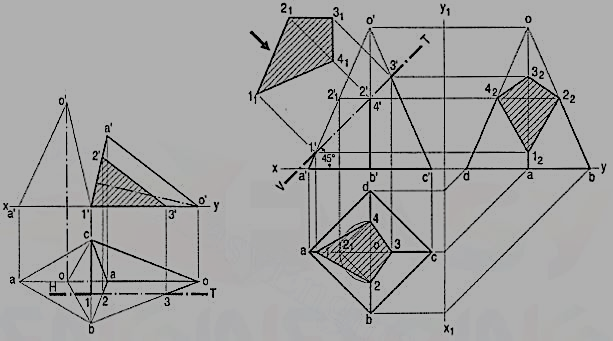
Problem 8 A pentagonal pyramid has its base on the H.P. and the edge of the base nearer the V.P., parallel to it. A vertical section plane, inclined at 45° to o the V.P., cuts the pyramid at 6 mm from the axis. Draw the top view, sectional front view and the auxiliary front view on an A. V.P. parallel to the section plane. Base of the pyramid 30 mm side; axis 50 mm long.
The section plane will be a line in the top view. It is to be at 6 mm from the axis.
i) Draw a circle with o as centre and radius equal to 6mm.
ii) Draw a line H.T. tangent to this circle and inclined at 45° to xy. It can be drawn in four different positions, of which any one may be selected.
iii) Project points 1, 2 etc. from the top view to the corresponding edges in the front view. Here again, point 2 cannot be projected directly. With centre o and radius o2 draw an arc cutting any one of the slant edges, say oc at 21. Project 21 to 2'1 on o'c'.
(iv) Through 2'1, draw a line parallel to the base, cutting o' b' at 2'. Then 2' is the required point. Complete the view. It will show the apparent section.
(v) Draw a reference line x1y1 parallel to the H.T. and project an auxiliary sectional front view which will show the true shape of the section also.
It consists of following three cases:
(1) Section plane parallel to the base
(2) Section plane parallel to the axis
(1) Section plane parallel to the base:
When a cylinder is cut by a section plane parallel to the base, the true shape of the section is a circle of the same diameter.
(2) Section plane parallel to the axis:
When a cylinder is cut by a section plane parallel to the axis, the true shape of the section is a rectangle, the sides of which are respectively equal to the length of the axis and the length of the section plane within the cylinder (fig. 10). When the section plane contains the axis, the rectangle will be of the maximum size.
Problem 9: A cylinder of 40 mm diameter, 60 mm height and having its axis vertical, is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. and intersecting the axis32 mm above the base. Draw its front view, sectional top view, sectional side view and true shape of the section.
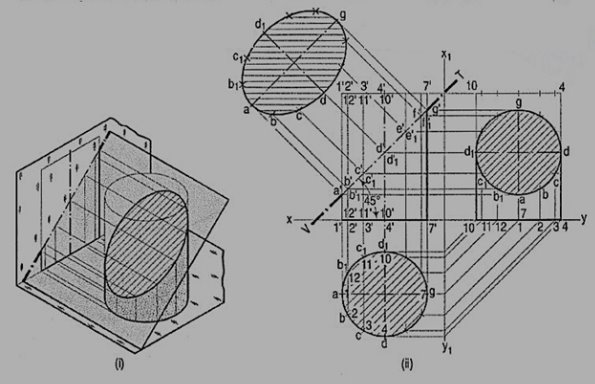
As the cylinder has no edges, many lines representing the generators may be assumed on its curved surface by dividing the base-circle into, say 12 equal parts.
(i) Name the points at which these lines are cut by the V.T. In the top view, these points lie on the circle and hence, the same circle is the top view of the section. The width of the section at any point, say c', will be equal to the length of the chord cc1 in the top view.
(ii) The true shape of the section may be drawn around the center line ag drawn parallel to V.T. as shown. It is an ellipse the major axis of which is equal to the length of the section plane viz. a'g', and the minor axis equal to the diameter of the cylinder viz. dd1.
(iii) Project the sectional side view as shown. The section will be a circle because the section plane makes 45° angle with xy.
Sections of Cones:
(1) Section plane parallel to the base of the cone.
(2) Section plane passing through the apex of the cone.
(3) Section plane inclined to the base of the cone at an angle smaller than the angle of inclination of the generators with the base.
(4) Section plane parallel to a generator of the cone.
(5) Section plane inclined to the base of the cone at an angle greater than the angle of inclination of the generators with the base.
(1) Section plane parallel to the base of cone:
The cone resting on the H.P. on its base [fig. 12(i)] is cut by a section plane parallel to the base. The true shape of the section is shown by the circle in the top view, whose diameter is equal to the length of the section viz. a'a'. The width of the section at any point, say b', is equal to the length of the chord bb1.
Problem:
fig. (ii) To locate the position in the top view of any given point p' in the front view of the above cone.
Method I:
(i) Through p', draw a line r'r' parallel to the base.
(ii) With o as center and diameter equal to r'r', draw a circle in the top view.
(iii) Project p' to points p and p1 on this circle. p is the top view of p'. p1 is the top view of another point p'1 on the back side of the cone and coinciding with p'. The chord pp1 shows the width of the horizontal section of the cone at the point p'. This method may be called the circle method.
Method II:
When the position of a point in the top view say q is given, its front view q' can be determined by reversing the above process.
(i) With centre o and radius oq, draw a circle cutting the horizontal centre line at s.
(ii) Through s, draw a projector cutting the slant side o'1' at s'.
(iii) Draw the line s's' parallel to the base, intersecting a projector through q at the required point q'.
(2) Section plane passing through the apex of the cone:
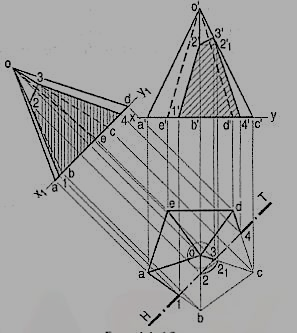
Problem
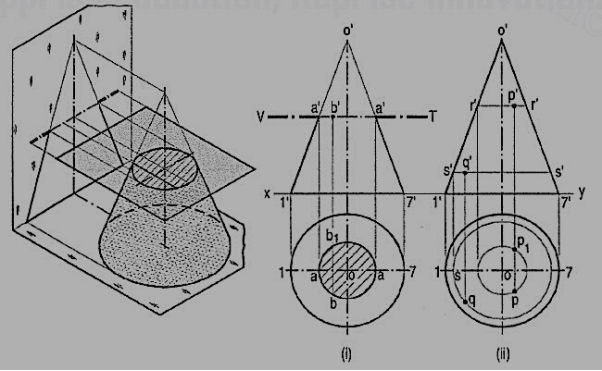
A cone, diameter of base 50 mm and axis 50 mm long is resting on its base on the H.P. It is cut by a section plane perpendicular to the V.P., inclined at 75° to the H.P. and passing through the apex. Draw its front view, sectional top view and true shape of the section.
Draw the projections of the cone and on it, show the line V. T. for the section plane.
Mark many points a', b' etc. on the V.T. and project them to points a, b etc. in the top view by the circle method. It will be found that these points lie on a straight line through o.
Thus, od is the top view of the line or generator o'd' and triangle odd1 is the top view of the section. The width of the section at any point b' on the section is the line bb1, obtained by projecting b' on this triangle. This method is called the generator method.
Project the true shape of the section. It is an isosceles triangle, the base of which is equal to the length of the chord on the base-circle and the altitude is equal to the length of the section plane within the cone.
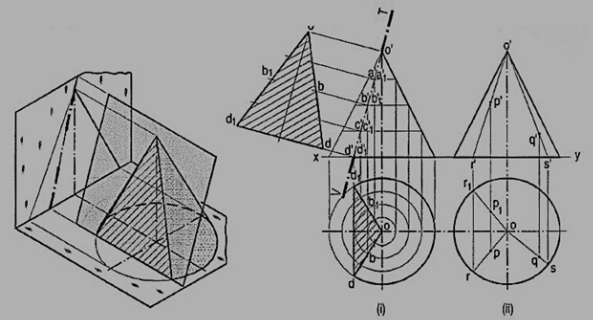
(3) Section plane inclined to the base of the cone at an angle smaller than the angle of inclination of the generators with the base:
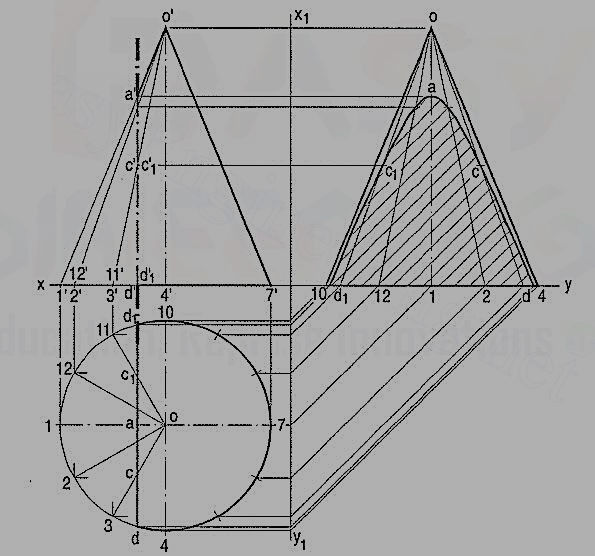
Problem 14-24. A cone, base 75 mm diameter and axis 80 mm long is resting on its base on the H.P. It is cut by a section plane perpendicular to the V.P., inclined at 45° to the H.P. and cutting the axis at a point 35 mm from the apex. Draw its front view, sectional top view, sectional side view and true shape of the section.
Draw a line V.T. in the required position in the front view of the cone.
(i) Generator method
(a) Divide the base-circle into many equal parts, say 12. Draw lines (i.e. generators) joining these points with o. Project these points on the line representing the base in the front view.
(b) Draw lines o' 2', o' 3' etc. cutting the line for the section at points b', c' etc. Project these points on the corresponding lines in the top view. For example, point b' on o' 2', also represents point b' 1 on o'-12' which coincides with o'-12'. Therefore, project b' to b on o 2 and to b1 on o'-12'. b and b1 are the points on the section (in the top view).
(c) Similarly, obtain other points. Point d' cannot be projected directly. Hence, the same method as in case of pyramids should be employed to determine the positions d and d1, as shown. In addition to these, two more points for the maximum width of the section at its centre should also be obtained. Mark m', the mid-point of the section and obtain the points m and m1. Draw a smooth curve through these points.
(d) The true shape of the section may be obtained on the V.T. as a new reference line or symmetrically around the centre line ag, drawn parallel to the V.T. as shown. It is an ellipse whose major axis is equal to the length of the section and minor axis equal to the width of the section at its centre.
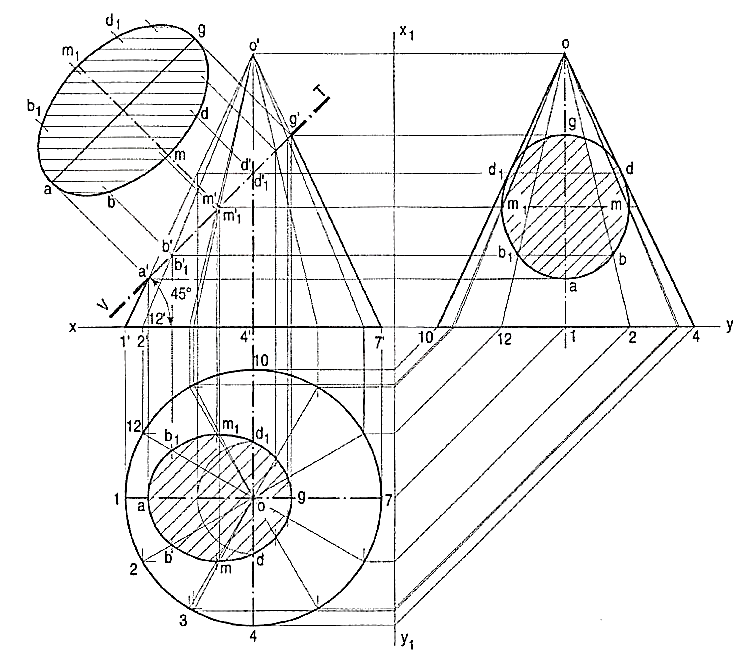
Draw the sectional side view by projecting the points on corresponding generators, as shown.
(ii) Circle method
(a) Divide the line of section into many equal parts. Determine the width of section at, and the position of each division-point in the top view by the circle method. For example, through c', draw a line c"c" parallel to the base.
(b) With o as centre and radius equal to half of c"c", draw an arc. Project c' to c and c1 on this arc. Then c and c1 are the required points. The straight-line joining c and c1 will be the width of the section at c'.
(c) Similarly, obtain all other points and draw a smooth curve through them. This curve will show the apparent section. The maximum width of the section will be at the mid-point e'. It is shown in the top view by the length of the chord joining e and e1.
(d) Draw a reference line x1 y1 parallel to the V.T. and project the true shape of the section. In the figure, the auxiliary sectional top view of the truncated cone is shown. It shows the true shape of the section.
The sectional side view may be obtained by projecting all the division-points horizontally and then marking the width of the section at each point, symmetrically around the axis of the cone.
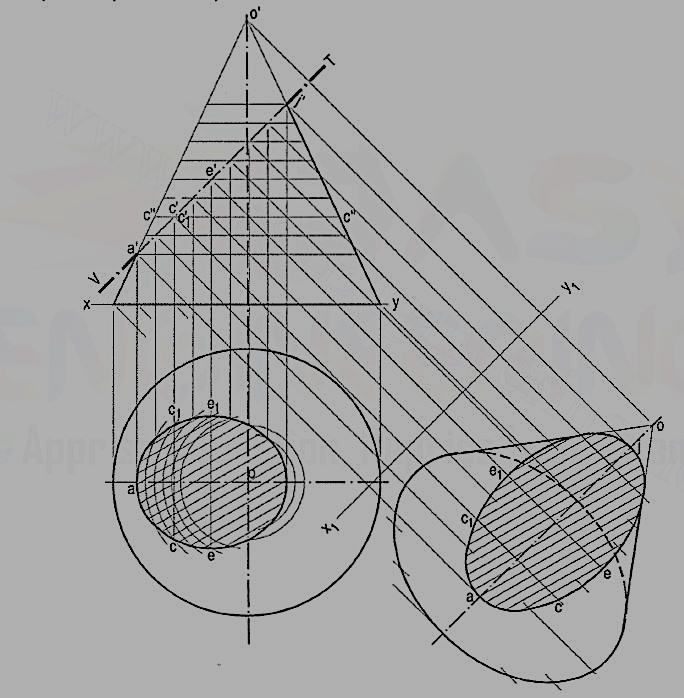
Section plane parallel to a generator of the cone:
Problem: The cone in same position as in fig, is cut by a section plane perpendicular to the V.P. and parallel to and 12 mm away from one of its end generators. Draw its front view, sectional top view and true shape of the section.
(i) Draw a line V.T. (for the section plane) parallel to and 12 mm away from the generator o' 1 '.
(ii) Draw the twelve generators in the top view and project them to the front view. All the generators except o' 1 ', o' 2' and o'-12' are cut by the section plane. Project the points at which they are cut, to the corresponding generators in the top view. The width of the section at the point where the base is cut will be the chord aa1. Draw a curve through a ...f... a1. The figure enclosed between aa1 and the curve is the apparent section.
(iii) Obtain the true shape of the section as explained in the previous problem.
It will be a parabola.
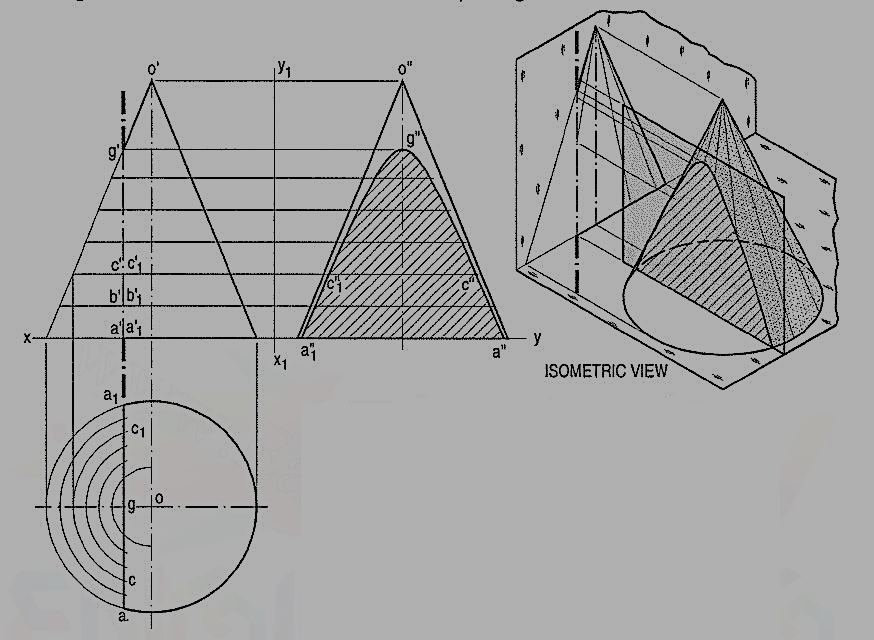
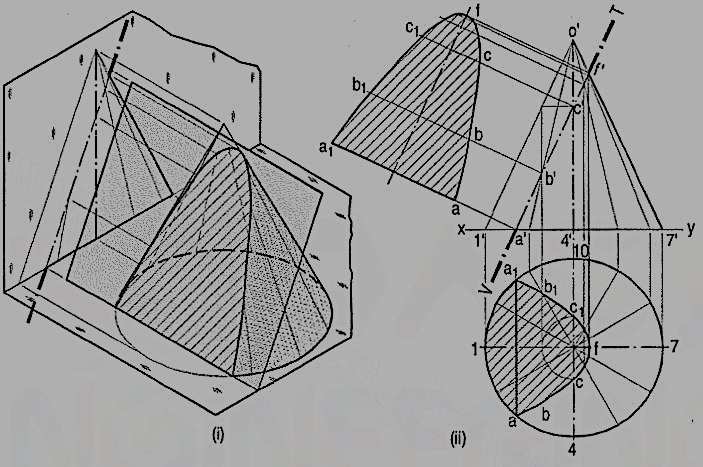
Section plane inclined to the base of the cone at an angle greater than the angle of inclination of the generators with the base:
Problem
Fig.: A cone, base 45 mm diameter and axis 55 mm long is resting on the H.P. on its base. It is cut by a section plane, perpendicular to both the H.P. and the V.P. and 6 mm away from the axis. Draw its front view, top view and sectional side view.
The section will be a line, perpendicular to xy, in both the front view and the top view. The side view will show the true shape of the section. The width of the section at any point, say c', will be equal to cc1 obtained by the circle method
(i) Draw the side view of the cone.
(ii) Project the points (on the section) in the side view taking the widths from the top view. For example, through c' draw a horizontal line. Mark on it points c"and c"1 equidistant from and on both sides of the axis so that c" c"1 = cc1.
(iii) Draw a curve through the points thus obtained. It will be a hyperbola.
Fig. shows the views obtained by the generator method.
True shape of section the true form of the cut surface is called true shape of section. It is obtained by viewing the object normal to the cut surface and projecting it on a plane parallel to the section plane.
A section will show its true shape when viewed in normal direction. To find the true shape of a section, it must be projected on a plane parallel to the section plane. For polyhedra, the true shape of the section depends on the number of POIs. The true shape of the section of a sphere is always a circle. Types of sections of solid.
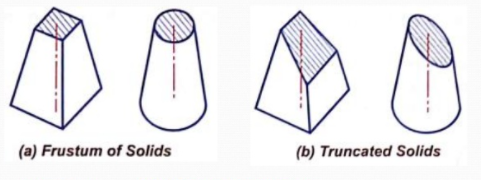
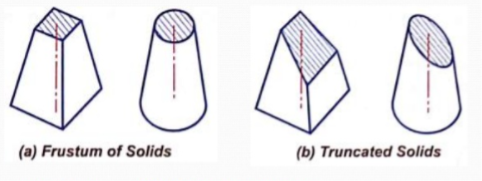
1) Frustum of a solid
When a solid is cut by a cutting plane parallel to its base, the portion obtained after removing the top portion is called Frustum solid.
2) Truncated solid
When a solid is cut by a cutting plane incline to its base, the portion obtained after removing the top portion is called truncated solid.

References:
1. A Text Book of Engineering Drawing: RK Dhawan, S Chand & Company
2. Engineering Drawing Plane and Solid Geometry: N.D. Bhatt, Charotar Publishing House.