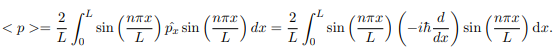Unit-7
Introduction to Quantum Mechanics
Contents:
Louis de- Broglie in 1924 extended the wave particle parallelism of light radiations to all the fundamental entities of Physics such as electrons, protons, neutrons, atoms and molecules etc. He put a bold suggestion that the correspondence between wave and particle should not confine only to electromagnetic radiation, but it should also be valid for material practices, i.e. like radiation, matter also has a dual (i.e., particle like and wave like) character.
A moving particle is always associated with the wave and the particle is controlled by waves. This suggestion was based on the fact that nature loves symmetry, if radiation like light can act like wave some times and like a particle at other times, then the material particles (e.g., electron, neutron, etc.) should act as waves at some other times. These waves associated with particles are named de- Broglie waves or matter waves.
Expression for de- Broglie wavelength
The expression of the wavelength associated with a material particle can be derived on the analogy of radiation as follows:
Considering the plank’s theory of radiation, the energy of photon (quantum) is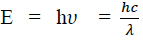 
Where c is the velocity of light in vacuum and is its wave length.
According to Einstein energy – mass relation
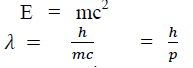
Where mc = p is momentum associated with photon.
If we consider the case of material particle of mass m and moving with a velocity v ,i.e momentum mv, then the wave length associated with this particle ( in analogy to wave length associated with photon ) is given by
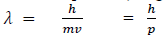
Time dependent equation:
It was observed that the wave function of a particle of fixed energy E could most naturally be written as a linear combination of wave functions of the form:
Now the hemiltonian of this system:
H=T+V
Where V is the potential energy and T is the kinetic energy. As we already know that ‘H’ is the total energy, we can rewrite the equation as:
Now taking the derivatives:
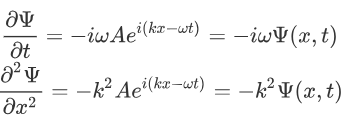
We know that:
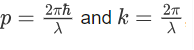
Where ‘λ’ is the wavelength and ‘k’ is the wavenumber.
We have:
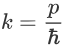
Therefore:
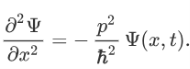
Now multiplying Ψ (x, t) to the Hamiltonian we get:
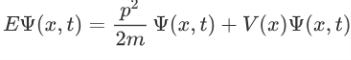
The above expression can be written as:
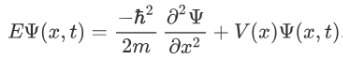
We already know that the energy wave of a matter wave is written as:
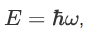
So, we can say that
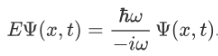
Now combining the right parts, we can get the Schrodinger Wave Equation.
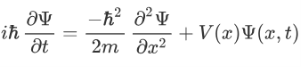
Time independent equation:
According to de-Broglie theory, for a particle of mass ‘m’, moving with a velocity ‘v’, the wavelength associated with it is
λ=h/p
The wave equation for a de-Broglie wave can be written in complex notation as:
…………1
Where, A is the amplitude, ω is angular frequency and k is the wave vector.
Differentiate equation (1) with respect to‘t’ twice, we get
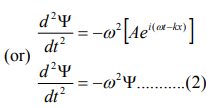
We have differential equation for the traveling wave as,
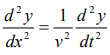……….3
Where, y is displacement and ‘v’ is velocity of wave.
By analogy, we can write the wave equation for de-Broglie wave associated with the motion of a free particle as,
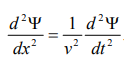………4
This represents the de-Broglie wave propagating along x-direction with a velocity ‘v’ and ‘Ψ’ is the displacement.
From equation (2) and (4),
…………..5
The kinetic energy of a moving particle of mass ‘m’ and velocity ‘v’ is given by
But we have from equation (1), p = (h/λ)
Substitute for (1/ λ)2 from equation (5),
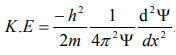…………….6
Let there be a field where the particle is present. Depending on its position in the field, the particle will possess certain potential energy. Then we can write:
Total energy = Kinetic energy + Potential energy
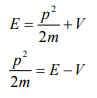
From equation (6), we can write
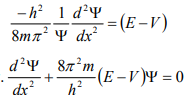
This is the time independent Schrödinger’s wave equation in one-dimension.
Let’s say you have a function of x, which we will call Ψ(x), and we can plot this wavefunction on a graph. The y axis represents the amplitude of the wave. If you square this, or write (amplitude of the wave) ^2 this is equal to the intensity of the wave.
However, the problem is that the wavefunction is complex, it is not necessarily real, i.e. it may have a part to it that is imaginary. Thus, instead of using Ψ^2, which would be impossible to work with, you instead use the complex conjugate of Ψ, which we call Ψ* by changing the sign of the imaginary part, and making it possible to work with mathematically. So now, to get the intensity of the wave, we no longer will use Ψ^2, but instead will use ΨΨ*, which is the absolute magnitude of Ψ^2. We can also plot Ψ(x)Ψ*(x) vs. x.
Let’s say we take just a segment on the graph between x and (x+dx), and the difference between those two points is just dx.
The Born Interpretation says that the wavefunction Ψ(x)Ψ*(x)dx will tell us the probability that the particle is located in the region between x and (x+dx). A region with a large value for Ψ(x)Ψ*(x) will have high probability for the particle in that region. We can normalize this function by taking the integral from negative infinity to positive infinity ofdx Ψ(x)Ψ*(x) and set that equal to 1, because that area encompasses 100% probability of where the particle must be.
Operators allow us to compute the expectation value of some physics quantity given the wavefunction. If a particle is in the state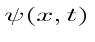 
, the normal way to compute the expectation value of 
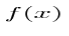is
We can move the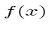 
between just before 
anticipating the use of linear operators.
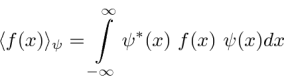
If the variable we wish to compute the expectation value of (like P) is not a simple function of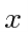 
, let its operator act on 
. The expectation value of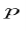 
in the state 
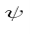is
 |
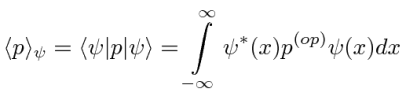The Dirac Bra-ket notation shown above is a convenient way to represent the expectation value of a variable given some state.
The simplest system in quantum mechanics has the potential energy V=0V=0 everywhere. This is called a free particle since it has no forces acting on it. We consider the one-dimensional case, with motion only in the xx-direction, giving the time-independent Schrödinger equation
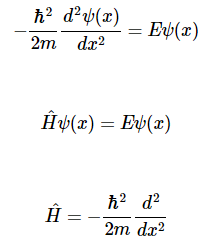
Possible solutions of Equation are
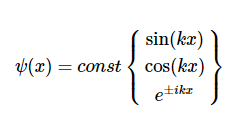
It is of interest also to consider the x-component of linear momentum for the free-particle solutions. The eigenvalue equation for momentum is
p^xψ(x)=−iℏdψ(x)/dx=pψ(x)
Where we have denoted the momentum eigen value as p.
The problem with using the wavefunctions to represent free particles is that plane sine waves extend to infinity in both spatial directions, so cannot represent a particle whose wavefunction is nonzero in a limited region of space. Physically, that it must have a wavefunction that goes to zero far away in either direction. A localized wavefunction of this type is called a “wavepacket”. We shall discover that a wavepacket can be constructed by adding plane waves together. To represent a localized particle, we must superpose waves having different wavelengths. Now, the plane waves we add together will individually be solutions of the Schrödinger equation.
If we add together two sine waves with frequencies close together, we get "beats." This pattern can be viewed as a string of wavepackets. For example, considering adding to sine waves together with spatial and temporal frequencies of (k±Δk,k±Δk) and (ω±Δω,ω±Δω), respectively.
Sin[(k−Δk)x−(ω−Δω)t] +sin[(k+Δk)x−(ω+Δω)t
If we use the trigonometric addition formula, the sum in Equation can be simplified to
2sin(kx−ωt) cos[(Δk)x−(Δω)t]
Equation 3.4.203.4.20 exhibits the phenomenon of beats between waves close in frequency. The first term, sin(kx−ωt)sin(kx−ωt), oscillates at the average of the two frequencies. It is modulated by the slowly varying second term, often called the “envelope function”, which oscillates once over a spatial extent of order π/Δkπ/Δk. This is the distance over which waves initially in phase at the origin become completely out of phase. Of course, going a further distance of order π/Δkπ/Δk, the waves will become synchronized again.
Statement:
It is impossible to determine simultaneously both the position and momentum of a quantum mechanical particle moving inside the wave packet with equal accuracy. In any simultaneous determination of the position and momentum of a particle, the product of the corresponding uncertainties inherently present in the measurement is equal to, greater than (h/4π).
Explanation:
Consider a quantum particle moving inside a wave packet of width Δx. Then inside the wave packet it is not possible to find the exact position of the particle and any attempt to measure it will have an uncertainty (error) which less than or equal to Δx.
The maximum uncertainty involved in measuring the position of the particle within the wave packet is Δx. Since position cannot be measured accurately, there will be an uncertainty in measuring momentum also.
According to Heisenberg’s uncertainty principle, the product of uncertainty involved in the measurement of these two quantities is given by the relation,
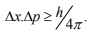
Where ∆x = uncertainty in position.
∆p = uncertainty in momentum.
It can be applied to any conjugate physical quantities such as energy and time, angular position and angular momentum etc.
Other forms of Uncertainties are:
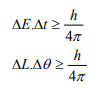
Where, ΔE, Δt are the uncertainties in the measurement of energy and time, and ΔL, Δθ are the uncertainties in the measurement of angular momentum and angular position.
We will now look at the solutions of a particle of mass m confined to move along the x-axis between 0 to L. This is achieved by making the potential 0 between x = 0 and x = L and V = ∞ for x < 0 and x > L. In quantum mechanics this model is referred to as particle in a box (PIB) of length L.
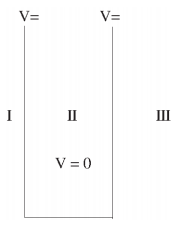
The one-dimensional infinite potential well of length L. It is divided into three regions, with regions I and III having V = ∞ and region II having V = 0
Before we set up and solve the Schrodinger equation let us apply de Broglie’s approach to this problem. De Broglie associates a wave with every material particle traveling with momentum p. The wavelength of the wave is
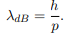
The classical analog of a particle in a box is a string that is fixed at both ends. When such a string is plucked, we know that the amplitude of the oscillations at the fixed ends is zero. In other words, an integer number of half-wavelengths must fit in the length of the box. Applying this idea to the present case, we find that
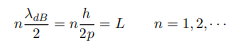
Solving for p we get
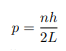
The particle feels no potential energy so all its energy is in the form of kinetic energy. As a result
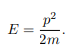
Substituting for p, we get
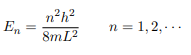
The Schrodinger equation is-
Hψˆ (x) = Eψ(x)
Where V (x) = ∞ in regions I and III and V (x) = 0 in region II. The results are in no way affected if in region II the potential is V because it only has the effect of altering the zero of energy and so without of generality, we will assume that V = 0 within the box. In regions I and III the wave function is identically zero since the potential is infinite so we will only have to consider the solution within the box.
We are looking for the solutions to the equation.
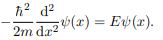
We rewrite this differential equation in the form:
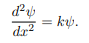
Wave equation
ψ(x) = A cos(kx) + B sin(kx)
The boundary conditions that the wave function should satisfy are
ψ (0) = 0 and ψ(L) = 0. The
First of these conditions implies that A = 0.
The second condition yields
B sin(kL) = 0
Which implies that kL = nπ, n = 1, 2, 3, ···
Or in other words k = nπ/L. Because E is related to k we hence obtain that
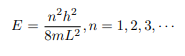
You will notice that the application of the boundary conditions naturally leads to quantization. In addition, observe that we do not consider n = 0 as a possibility because that would imply that the wave function is identically zero for all x or in other words there is no particle! The constant B is yet to be determined. The normalization condition on the wave function yields B.
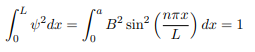
In cases where the wave function is not an eigen function of the operator corresponding to the observable, we will be concerned with the statistical mean of the measured values, averaged over a large number of measurements, the expectation value. The expectation value is defined of an operator is defined a:
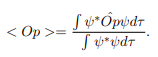
The average momentum is the
