Unit 5
Magneto static in a linear magnetic medium
Contents:
The Biot-Savart Law relates magnetic fields to the currents which are their sources. In a similar manner, Coulomb's law relates electric fields to the point charges which are their sources. Finding the magnetic field resulting from a current distribution involves the vector product, and is inherently a calculus problem when the distance from the current to the field point is continuously changing.

See the magnetic field sketched for the straight wire to see the geometry of the magnetic field of a current.
Each infinite small current element makes a contribution to the magnetic field at point P which is perpendicular to the current element, and perpendicular to the radius vector from the current element to the field point P.

The relationship between the magnetic field contribution and its source current element is called the Biot-Savart law.
The direction of the magnetic field contribution follows the right hand rule illustrated for a straight wire. This direction arises from the vector product nature of the dependence upon electric current.
Some examples of geometries where the Biot-Savart law can be used to advantage in calculating the magnetic field resulting from an electric current distribution.

The Curl of a Magnetic Field
From the equation, we can generate an expression for the curl of a magnetic field. Stokes' Theorem states that:
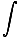 B·ds =
B·ds = 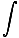 curl B·da
curl B·da
We have already established that 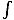 B·ds =
B·ds = 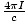 .
.
Thus:
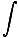 Curl B·Da =
Curl B·Da = 
To remove the integral from this equation we include the concept of current density, J. Recall that I = 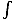 J·Da. Substituting this into our equation, we find that
J·Da. Substituting this into our equation, we find that
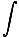 Curl B·Da =
Curl B·Da = 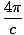
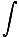 J·Da
J·Da
Clearly, then:
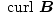 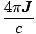 |
|
Thus, the curl of a magnetic field at any point is equal to the current density at that point. This is the simplest statement relating the magnetic field and moving charges. It is mathematically equivalent to the line integral equation we developed before, but is easier to work with in a theoretical sense.
The Divergence of the Magnetic Field
Recall that the divergence of the electric field was equal to the total charge density at a given point. We have already examined qualitatively that there is no such thing as magnetic charge. All magnetic fields are, in essence, created by moving charges, not by static ones. Thus, because there are no magnetic charges, there is no divergence in a magnetic field:
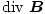 |
|
This fact remains true for any point in any magnetic field. Our expressions for divergence and curl of a magnetic field are sufficient to describe uniquely any magnetic field from the current density in the field. The equations for divergence and curl are extremely powerful; taken together with the equations for the divergence and curl for the electric field, they are said to encompass mathematically the entire study of electricity and magnetism.
Magnetic vector potential, A, is the vector quantity in classical electromagnetism defined so that its curl is equal to the magnetic field.
Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
a uniform magnetic field B⃗ =Bzz^
We have the relation connecting the magnetic field vector B⃗and the vector potential A⃗
B⃗ =∇×A⃗
Now, according to Stokes’s theorem, we have
∫S(∇×A⃗) ⋅dS⃗ =∮CA⃗ ⋅dr⃗
The theorem can be stated as follows: The surface integral of the curl of a vector field is equal to the line integral of the vector field around the boundary of the surface. So, in the above equation, the surface integral is across the surface SS bounded by a boundary curve CC, along which the line integral is taken.
Now,
∮CA⃗ ⋅dr⃗ =∫SB⃗ ⋅dS⃗
Since the magnetic field is uniform and points in a direction along the axis of the cylinder, the magnetic vector potential lies along the radial direction. At the end, the magnetic field points in the samedirection as the cross-sectional area of the hollow cylinder. Hence the dot product simplifies as
∮CA⃗ ⋅dr⃗ =Bz∫SdS
If we choose our origin on an axis of symmetry, so that we can take AA as circumferential (ϕ^ component only) and a function only of r, then
∮CA⃗ ⋅dr⃗ =Aϕ(2πr)
Magnetization, also termed as magnetic polarization, is a vector quantity that gives the measure of the density of permanent or induced dipole moment in a given magnetic material. As we know, magnetization results from the magnetic moment, which results from the motion of electrons in the atoms or the spin of electrons or the nuclei. The net magnetization results from the response of a material to the external magnetic field, together with any unbalanced magnetic dipole moment that is inherent in the material due to the motion in its electrons as mentioned earlier. The concept of magnetization helps us in classifying the materials on the basis of their magnetic property. In this section, we will learn more about magnetization and the concept of magnetic intensity.
The magnetization of a given sample material M can be defined as the net magnetic moment for that material per unit volume.
Mathematically,
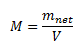
Let us now consider the case of a solenoid. Let us take a solenoid with n turns per unit length and the current passing through it be given by I, then the magnetic field in the interior of the solenoid can be given as,
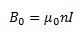
Now, if we fill the interior with the solenoid with a material of non-zero magnetization, the field inside the solenoid must be greater than before. The net magnetic field B inside the solenoid can be given as,
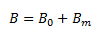
Where Bm gives the field contributed by the core material. Here, Bm is proportional to the magnetization of the material, M. Mathematically,
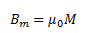
Here, µ0 is the constant of permeability of a vacuum.
Let us now discuss another concept here, the magnetic intensity of a material. The magnetic intensity of a material can be given as,

From this equation, we see that the total magnetic field can also be defined as,
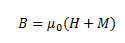
Here, the magnetic field due to the external factors such as the current in the solenoid is given as H and that due to the nature of the core is given by M. The latter quantity, that is M is dependent on external influences and is given by,
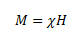
Where χ is the magnetic susceptibility of the material. It gives the measure of the response of a material to an external field. The magnetic susceptibility of a material is small and positive for paramagnetic materials and is small and negative for diamagnetic materials.
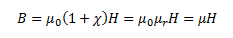
Here, the term µr is termed as the relative magnetic permeability of a material, which is analogous to the dielectric constants in the case of electrostatics. We define the magnetic permeability as,
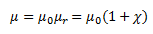
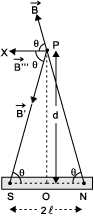
- Magnetic field strength at a point due to a bar magnet on the axial line
Let NS be a bar magnet of length 2l and centre O. Let point P lies on the axial line at distance d from O.
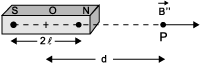 |
- If m is the pole strength, then magnetic field strength of point P due to N pole of the magnet is
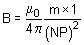
 ... (i)
... (i)
Similarly magnetic field strength at point P due to S pole is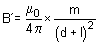 ... (ii)
... (ii)
So net magnetic field strength at point P
B = B – B’’
Using equations (i) and (ii)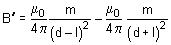
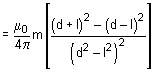

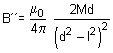 ... (iii)
... (iii)
When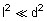
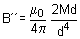
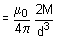 ... (iv)
... (iv)
Direction of B’’ is along SN. - Magnetic field strength at a point due to a bar magnet on the equatorial line
When point P lies on the equatorial line of a bar magnet NS at a distance OP = d, magnetic field strength at point P due to N pole of the magnet is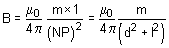
 |
- Similarly, magnetic field strength at point P due to S pole of the magnet is
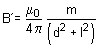
Since B = B’’in magnitude, so net magnetic field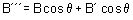

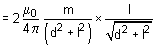
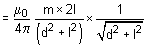
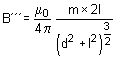
 ... (v)
... (v)
If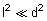
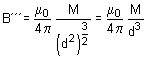 ... (vi)
... (vi)
Direction of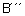 is along PX.
is along PX.
Now from equation (iv) and (vi)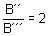
or 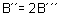
So it can be concluded that the magnetic field due to a short bar magnet at any point on the axial line is twice the magnetic field at a point on the equatorial line of that magnet at the same distance.
In a large class of materials, there exists an approximately linear relationship between  and
and  . If the material is isotropic then
. If the material is isotropic then
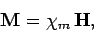 |
|
Where  is called the magnetic susceptibility. If
is called the magnetic susceptibility. If 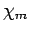 is positive then the material is called paramagnetic, and the magnetic field is strengthened by the presence of the material. On the other hand, if
is positive then the material is called paramagnetic, and the magnetic field is strengthened by the presence of the material. On the other hand, if  is negative then the material is diamagnetic, and the magnetic field is weakened in the presence of the material. The magnetic susceptibilities of paramagnetic and diamagnetic materials are generally extremely small.
is negative then the material is diamagnetic, and the magnetic field is weakened in the presence of the material. The magnetic susceptibilities of paramagnetic and diamagnetic materials are generally extremely small.
A linear relationship between 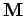 and
and  also implies a linear relationship between
also implies a linear relationship between 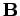 and
and  . In fact, we can write
. In fact, we can write
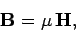 |
|
Where
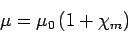 |
|
Is termed the magnetic permeability of the material in question. (Likewise, 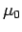 is termed the permeability of free space.) Note that
is termed the permeability of free space.) Note that 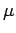 has the same units as
has the same units as 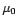 . It is clear that the permeabilities of common diamagnetic and paramagnetic materials do not differ substantially from the permeability of free space. In fact, to all intents and purposes, the magnetic properties of such materials can be safely neglected (i.e.,
. It is clear that the permeabilities of common diamagnetic and paramagnetic materials do not differ substantially from the permeability of free space. In fact, to all intents and purposes, the magnetic properties of such materials can be safely neglected (i.e.,  ).
).
The magnetic materials are generally classified into three types based on the behaviour of materials in a magnetising field. They are diamagnetic, paramagnetic and ferromagnetic materials which are dealt with in this section.
a) Diamagnetic materials
The orbital motion of electrons around the nucleus produces a magnetic field perpendicular to the plane of the orbit. Thus, each electron orbit has finite orbital magnetic dipole moment. Since the orbital planes are oriented in random manner, the vector sum of magnetic moments is zero and there is no resultant magnetic moment for each atom.
In the presence of an external magnetic field, some electrons are speeded up and some are slowed down. The electrons whose moments were anti-parallel are speeded up according to Lenz’s law and this produces an induced magnetic moment in a direction opposite to the field. The induced moment disappears as soon as the external field is removed.
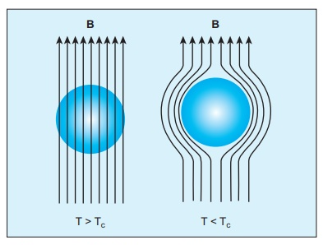
When placed in a non-uniform magnetic field, the interaction between induced magnetic moment and the external field creates a force which tends to move the material from stronger part to weaker part of the external field. It means that diamagnetic material is repelled by the field.
This action is called diamagnetic action and such materials are known as diamagnetic materials. Examples: Bismuth, Copper and Water etc.
The properties of diamagnetic materials are
- Magnetic susceptibility is negative.
- Relative permeability is slightly less than unity.
- The magnetic field lines are repelled or expelled by diamagnetic materials when placed in a magnetic field.
- Susceptibility is nearly temperature independent.
(b) Paramagnetic materials
In some magnetic materials, each atom or molecule has net magnetic dipole moment which is the vector sum of orbital and spin magnetic moments of electrons. Due to the random orientation of these magnetic moments, the net magnetic moment of the materials is zero.
In the presence of an external magnetic field, the torque acting on the atomic dipoles will align them in the field direction. As a result, there is net magnetic dipole moment induced in the direction of the applied field. The induced dipole moment is present as long as the external field exists.
When placed in a non-uniform magnetic field, the paramagnetic materials will have a tendency to move from weaker to stronger part of the field. Materials which exhibit weak magnetism in the direction of the applied field are known as paramagnetic materials. Examples: Aluminium, Platinum and chromium etc.
The properties of paramagnetic materials are:
- Magnetic susceptibility is positive and small.
- Relative permeability is greater than unity.
- The magnetic field lines are attracted into the paramagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
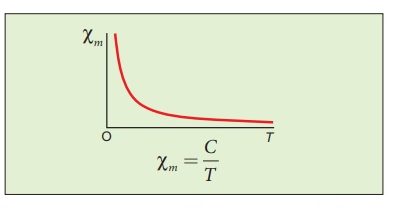
Curie’s law
When temperature is increased, thermal vibration will upset the alignment of magnetic dipole moments. Therefore, the magnetic susceptibility decreases with increase in temperature. In many cases, the susceptibility of the materials is
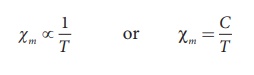
This relation is called Curie’s law. Here C is called Curie constant and temperature T is in kelvin. The graph drawn between magnetic susceptibility and temperature is shown in Figure 3.26, which is a rectangular hyperbola.
(c)Ferromagnetic materials
An atom or a molecule in a ferromagnetic material possesses net magnetic dipole moment as in a paramagnetic material. A ferromagnetic material is made up of smaller regions, called ferromagnetic domain. Within each domain, the magnetic moments are spontaneously aligned in a direction. This alignment is caused by strong interaction arising from electron spin which depends on the inter-atomic distance. Each domain has net magnetisation in a direction.However, the direction of magnetisation varies from domain to domain and thus net magnetisation of the specimen is zero.
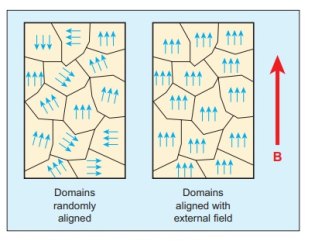
In the presence of external magnetic field, two processes take place
1. The domains having magnetic moments parallel to the field grow in size
2. The other domains (not parallel to field) are rotated so that they are aligned with the field.
Domains: We know magnets aren’t attracted to everything; if we put a magnet on a wooden wall, it will fall right down. Generally, magnets are attracted to objects that are made of the metals iron, nickel, or cobalt. These materials are called ferromagnetic materials. The reason magnets stick to these metals is because of a special characteristic about the atoms inside these metals. In most other materials that are not magnetic, the magnetic moments of the atoms inside are all oriented in random directions that cancel each other out. In ferromagnetic materials, the atoms form structures called domains. A domain is a region inside of a material where groups magnetic moments naturally align in the same direction.


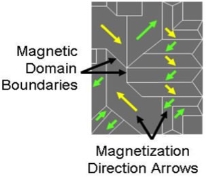
There can be numerous domains within an object. When there is no external magnetic field present, the domains are also oriented randomly so that there is no net magnetic field. However, when an external magnetic field is present, the domains will rotate and align with the external magnetic field. When all or most of the domains are aligned in the same direction, the whole object becomes magnetized in that direction and becomes a magnet.


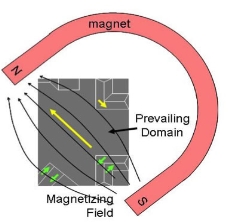
The process of using a magnetic field to magnetize another object is called induction. Once a magnet has been induced, it produces its own magnetic field as long as its domains are aligned.
Hysteresis
Once we have induced a magnet, we can observe an interesting effect when the external magnetic field is removed. Depending on the material, the domains will stay lined up together in the same direction even after the external field is gone. The domains do not instantly return to normal. This tendency to stay aligned is called hysteresis. Hysteresis is what allows us to make permanent magnets. To make permanent magnets, we take our material, create whatever shape we want, and then place the material inside of a very strong magnetic field. The domains inside the material align with the magnetic field, and when we remove the field, the domains stay aligned, and we now have a new magnet. While these are magnets are not truly “permanent”, some magnets’ domains will not return to their original state for much longer than a single lifetime.