Unit 4
Electrostatics in vacuum and dielectric medium
Contents
Distribution
Charge at the centre of a dielectric sphere
Suppose, a system of charges having charges as q1, q2, q3……. Up to qn. We can easily find out the net charge by adding charges algebraically.
Net electric field and net force can be obtained by using the principle of superposition. The continuous charge distribution system is a system in which the charge is uniformly distributed over the conductor. In continuous charge system, infinite numbers of charges are closely packed and have minor space between them.
Unlikely from the discrete charge system, the continuous charge distribution is uninterrupted and continuous in the conductor. There are three types of the continuous charge distribution system. Types of continuous charged distributions:
1. Linear Charge Distribution
2. Surface Charge Distribution
3. Volume charge distribution
Linear Charge Distribution:
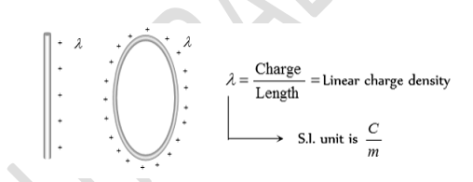
When the distribution of charge is uniformly along the line then it is called Linear Charge Distribution. e.g. Line making the circumference of a circle, straight line, etc. Here we define a new physical quantity called the linear charge density, It is denoted by symbol ‘λ’ and is given by---
λ = dq / dl.
And Such that total charge on the distribution is
q =∫ λ dl
It is measured in Cm-1. Let us take a small element having length dl of the line. The small amount of charge on this element is dq= λ. Dl
Surface Charge Distribution:
When charge is distributed uniformly over some area it is called surface charge distribution.
For example, a charged thin sheet. The surface charge density σ of a wire is given as where Δs is a small area element of a charged sheet and ΔQ is the charge contained in that area element. The unit for σ is C/m2.
Also, dq =σ ds and q =∫σ ds
Volume Charge Density:
Volume Charge Density is defined as continuous charge distribution over a volume.
For example, a metal sphere or cylinder etc. The volume charge density or simply called charge density ρ is given as

Where ΔV is a small volume element of a charged sphere on macroscopic scale and ΔQ is the charge contained in that volume element. The unit for ρ is C/m3 or coulomb per cubic metre

Also, dq = ρ dv and q = ∫ρ dv
The electric field of an infinite line charge with a uniform linear charge density can be obtained by a using Gauss' law. Considering a Gaussian surface in the form of a cylinder at radius r, the electric field has the same magnitude at every point of the cylinder and is directed outward. The electric flux is then just the electric field times the area of the cylinder.


|
|
Electric Field:
Sheet of Charge
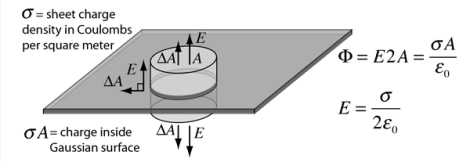
For an infinite sheet of charge, the electric field will be perpendicular to the surface. Therefore only the ends of a cylindrical Gaussian surface will contribute to the electric flux . In this case a cylindrical Gaussian surface perpendicular to the charge sheet is used. The resulting field is half that of a conductor at equilibrium with this surface charge density.
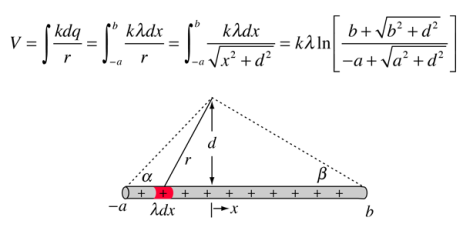
The potential of a line of charge can be found by superposing the point charge potentials of infinitesmal charge elements. It is an example of a continuous charge distribution.
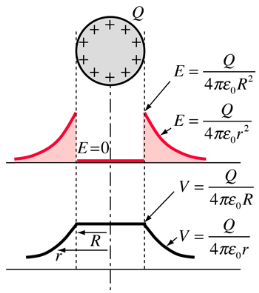
Potential: Charged Conducting Sphere
The use of Gauss' law to examine the electric field of a charged sphere shows that the electric field environment outside the sphere is identical to that of a point charge. Therefore the potential is the same as that of a point charge:
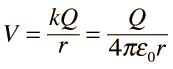
The electric field inside a conducting sphere is zero, so the potential remains constant at the value it reaches at the surface:
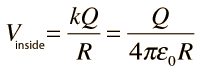
One approach to continuous charge distributions is to define electric flux and make use of Gauss' law to relate the electric field at a surface to the total charge enclosed within the surface. This involves integration of the flux over the surface.
Another approach is to relate derivatives of the electric field to the charge density. This approach can be considered to arise from one of Maxwell's equations and involves the vector calculus operation called the divergence. The divergence of the electric field at a point in space is equal to the charge density divided by the permittivity of space.
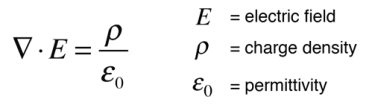
In a charge-free region of space where r = 0, we can say
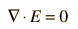
While these relationships could be used to calculate the electric field produced by a given charge distribution, the fact that E is a vector quantity increases the complexity of that calculation. It is often more practical to convert this relationship into one which relates the scalar electric potential to the charge density. This gives Poisson's equation and Laplace’s equation.
The curl of a vector field E = E(x, y, z) is defined, in terms of the deloperators∇, like a cross product
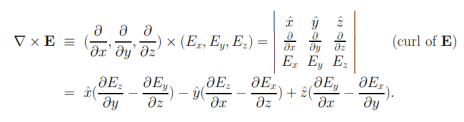
The proof of curl-free nature of static electric fields can be given by first showing that Coulomb field of a static charge is curl-free, and then making use of the superposition principle along with the fact that the curl of a sum must be the sum of curls — like differentiation, “taking curl” is a linear operation
t ∇× E = 0
with the Coulomb field of a point charge Q located at the origin.
A useful approach to the calculation of electric potentials is to relate that potential to the charge density which gives rise to it. The electric field is related to the charge density by the divergence relationship

And the electric field is related to the electric potential by a gradient relationship
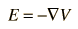
Therefore, the potential is related to the charge density by Poisson's equation
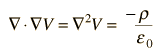
In a charge-free region of space, this becomes Laplace’s equation
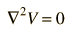
This mathematical operation, the divergence of the gradient of a function, is called the Laplacian. Expressing the Laplacian in different coordinate systems to take advantage of the symmetry of a charge distribution helps in the solution for the electric potential V. For example, if the charge distribution has spherical symmetry, you use the LaPlacian in spherical polar coordinates.
Since the potential is a scalar function, this approach has advantages over trying to calculate the electric field directly. Once the potential has been calculated, the electric field can be computed by taking the gradient of the potential.
Poisson's equation is
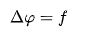
where is the Laplace operator, and are real or complex?
Valued functions on a manifold. Usually, is given and is sought. When the manifold is Euclidean space, the Laplace operator is often denoted as ∇2 and so Poisson's equation is frequently written as
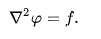
In three-dimensional Cartesian coordinates, it takes the form
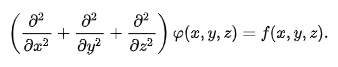
When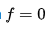
identically we obtain Laplace's equation
Poisson's equation may be solved using a Green's function:
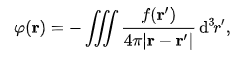
Where the integral is over all of space. A general exposition of the Green's function for Poisson's equation is given in the article on the screened Poisson equation. There are various methods for numerical solution, such as the relaxation method, an iterative algorithm
- First law: Like charges of electricity repel each other, whereas unlike charges attract each other.
- Second law: According to this law, the force exerted between two point charges
i) is directly proportional to the product of their strengths.
ii) is inversely proportional to the square of the distance between them. And
iii) is inversely proportional to the absolute permittivity of the surrounding medium.
This is known as Coulomb's Law
Electrostatic phenomena arise from the forces that electric charges exert on each other and are described by Coulomb’s law. Even though electrostatically induced forces seem to be rather weak.
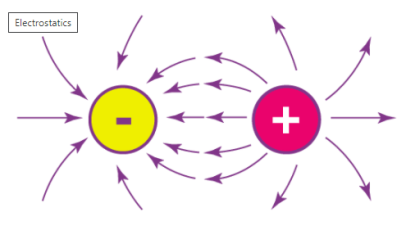
We begin with the magnitude of the electrostatic force between two-point charges q and Q. It is convenient to label one of these charges, q, as a test charge, and call Q a source charge. As we develop the theory, more source charges will be added. If r is the distance between two charges, then the force of electrostatic formula is:
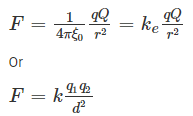
Electric field
Electric field lines are useful for visualizing the electric field. Field lines begin on positive charge and terminate on negative charge. Electric field lines are parallel to the direction of the electric field, and the density of these field lines is a measure of the magnitude of the electric field at any given point.
We show charge with “q” or “Q” and smallest unit charge is 1.6021 x 10-19 Coulomb (C). One electron and a proton have same amount of charge.
Positively Charged Particles
In this type of particles, numbers of positive ions are larger than the numbers of negative ions. Means, the numbers of protons are larger than the number of electrons. To neutralize positively charged particles, electrons from the surroundings come to this particle until the number of protons and electrons become equal.
Negatively Charged Particles
Similarly, numbers of electrons are larger than the number of protons. To neutralize negatively charged particles, since protons cannot move and cannot come to negatively charged particles, electrons moves to the ground or any other particle around
Neutral Particles: Include equal numbers of protons and electrons. They have both protons, neutrons and electrons however, numbers of positive ions are equal to the numbers of negative ions.
Dielectric Polarisation
A dielectric may be made up of polar or non-polar molecules. But the net effect of an external field is almost the same, i.e., the external field will compel the molecules to align their dipole moments along its own direction.
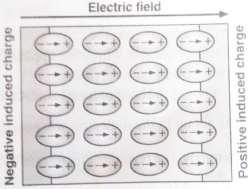
Let us consider a dielectric slab in an electric field which is acting in the direction shown in the figure. The arrangement of charges within the molecules of the dielectric in the electric field is as shown in the figure. The positive charges move in the direction of the field and the negative charges in the opposite direction. In other words, the electric dipoles align themselves with the direction of the field. In this state, the entire dielectric and its molecules are said to be polarised.
The alignment of the dipole moments of the permanent or induced dipoles with the direction of the applied electric field is called polarisation.
Within the two extremely thin surface layers indicated by shaded regions, there is an excess negative charge in one layer and an excess equal positive charge in the other layer.
The induced charges on the surfaces of the dielectric are due to these layers. These charges are not free but each is bound to a molecule lying in or near the surface. That is why these charges are called bound charges or fictitious charges. Within the remaining dielectric, the net charge per unit volume remains zero. Thus, although the dielectric is polarized, yet as a whole, it remains electrically neutral.
The positive induced surface charge must be equal in magnitude to the negative induced surface charge. Thus, in polarisation, the internal state of the slab is characterised not by an excess charge but by the relative displacement of the charges within it.
Polarisation can thus also be thought of as a phenomenon in which an alignment of positive and negative charges takes place within the dielectric resulting in no net increase in the charge of the dielectric.
The extent to which a dielectric is polarized is described by a vector quantity P called the polarisation.
Polarisation is defined as the electric dipole moment per unit volume.
P has the same direction as the molecular dipole moment.
In electrostatics, the permeability is the measure of the ability of the material to allow the formation of magnetic lines of force or magnetic field within. It speaks on the ability of magnetization that a material possesses for the applied magnetic field. In simpler words, we can define magnetic permeability as “the extent to which magnetic field lines can enter substance.” or “The power of conducting magnetic field lines by a substance.” It is denoted by the Greek alphabet μ. Following is the table with the mathematical representation of permeability, SI unit, and dimensional formula:

The permeability of free space is called Permeability constant and has the value μ0 = 4𝝅×10-7 H/m
It is a scalar quantity of isotropic medium and second rank tensor for anisotropic medium. Magnetic permeability plays an important role in classifying the magnetization property of a material. The material is said to be diamagnetic if its magnetic permeability is less than μ0. Similarly, the material is said to be paramagnetic if its magnetic permeability is greater than μ0.
Dielectric constant, also called relative permittivity or specific inductive capacity, property of an electrical insulating material (a dielectric) equal to the ratio of the capacitance of a capacitor filled with the given material to the capacitance of an identical capacitor in a vacuum without the dielectric material. The insertion of a dielectric between the plates of, say, a parallel-plate capacitor always increases its capacitance, or ability to store opposite charges on each plate, compared with this ability when the plates are separated by a vacuum. If C is the value of the capacitance of a capacitor filled with a given dielectric and C0 is the capacitance of an identical capacitor in a vacuum, the dielectric constant, symbolized by the Greek letter kappa, κ, is simply expressed as κ = C/C0. The dielectric constant is a number without dimensions. In the centimetre-gram-second system, the dielectric constant is identical to the permittivity. It denotes a large-scale property of dielectrics without specifying the electrical behaviour on the atomic scale.
Polar Molecules
A polar molecule is one in which the ‘centres of gravity’ of the positive charges (i.e., protons) and negative charges (i.e., electrons) do not coincide. Such molecules are called permanent electric dipoles as these have permanent dipole moments. Some common polar molecules are HCl, H2O, N2O, NH3, H2S, C2H5OH, SO2.
In a molecule of HCl, there is an excess positive charge on the H-ion and an equal negative charge on the Cl-ion. The molecule, therefore, has a dipole moment at every instant and is a polar molecule. Another interesting example of polar molecules is H2O.
In the water molecule, two O-H bonds are not placed opposite to each other (unlike the CO2 molecule) but are inclined at an angle of about 105°. The hydrogen ion forms a dipole moment with each of the oxygen ion,
(i) In the absence of an electric field, the electric dipole moments of these polar molecules point in random directions [Fig. (b)] and cancel each other. Therefore, even though each molecule has a dipole moment, the average moment per unit volume is zero.
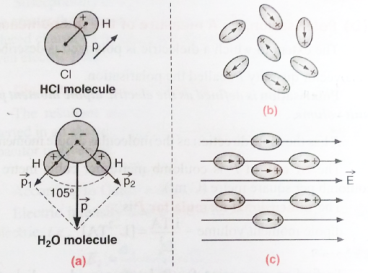
(ii) On the application of an electric field, the dipole moments of these molecules align themselves parallel, to the direction of the electric field as shown in figure (c). But this alignment is incomplete due to the thermal vibrations of the molecules. It is obvious that the alignment of the molecules with the applied field increases if:
- The electric intensity of the field is increased.
- Temperature is decreased.
It should be noted that increased electric intensity may also increase the dipole moment. It is due to the reason that with increased electric intensity, the distance between the centres of gravity of the positive and negative charges increases which results in an increase in the dipole moment.
A non-polar molecule is one in which the centres of gravity of positive charges (i.e., protons) and negative charges (i.e., electrons) coincide. These molecules, thus, do not have any permanent dipole moment.
Some common examples of non-polar molecules are CO2, CCl4, oxygen (O2), nitrogen (N2), hydrogen (H2), methane (CH4) and ethane (C2H6).
In a molecule of CO2, the oxygen ions are symmetrically placed with respect to the carbon ion, hence the dipole moment is zero

In CCl4, the external electric field changes the orientation of the C-Cl bond and thus produces induced dipole moment.
Thus, in general, when a non-polar molecule is placed in an electric field, the centres of positive and negative charges get displaced and the molecule is then said to have been polarized as shown in fig. (d). Such a molecule is then called the induced electric dipole and its electric dipole moment is called the induced electric dipole moment. As soon as the electric field is removed, the induced electric dipole moment disappears.
In the case of a spherical dielectric cavity, the problem can be solved very easily. Without loss of any generality, let us consider a dielectric sphere of radius a with a point charge q being located on the x-axis at a distance rs < a from the centre of the sphere,
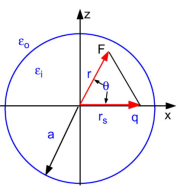
When λ = 0, the analytical solution to this classical electrostatic problem by the famous Kirkwood expansion is well-documented in the literature. More precisely, with respect to a spherical coordinate system (r, θ, ϕ) with its origin at the centre of the sphere (the pole is denoted by the x-axis in this note), due to the azimuthal symmetry, the electrostatic potential at an observation point r=(r, θ, ϕ) is
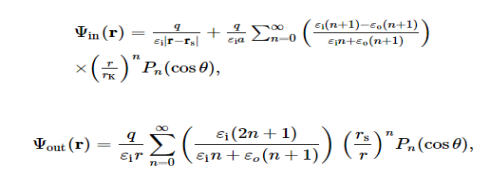
Where Pn(x) is the Legendre polynomial, and rK = a2/rs.
When λ≠ 0, the problem can be solved analytically by using the classical electrostatic theory as well. The exact solution is in fact given as
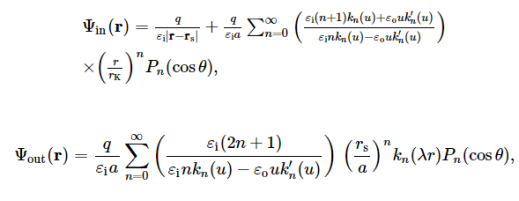
where u = λa, and kn(r) is the modified spherical Hankel function of order n (also called the modified spherical Bessel function of the second or third kind) defined as
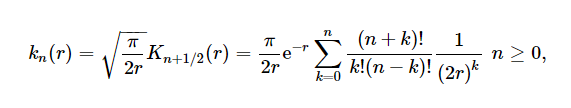
Where Kn(x) is the modified Bessel function of the third kind.
, when the ionic strength of the solvent, or equivalently the inverse Debye screening length λ, tends to zero and can be identified with and, respectively.