Unit 2
Mechanics of Solids
Contents
For an object rotating about an axis, every point on the object has the same angular velocity. The tangential velocity of any point is proportional to its distance from the axis of rotation. Angular velocity has the units rad/s.
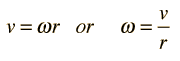
Angular velocity is the rate of change of angular displacement and can be described by the relationship
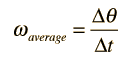
And if v is constant, the angle can be calculated from
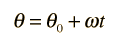
Angular velocity can be considered to be a vector quantity, with direction along the axis of rotation in the right-hand rule sense
The angular displacement is defined by:
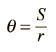
For a circular path it follows that the angular velocity is
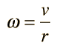
And the angular acceleration is
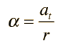
Where the acceleration here is the tangential acceleration.
In addition to any tangential acceleration, there is always the centripetal acceleration:
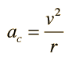
For objects that rotate with a constant angular acceleration, there are a few equations, called the kinematic equations for angular motion, that you can use to determine the angular position or angular velocity of the object at any point in time.
|
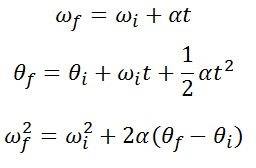
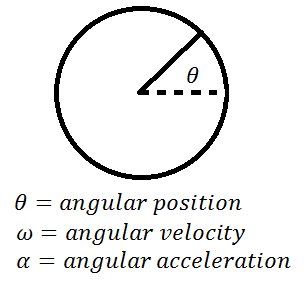
Before you can use these equations correctly, you have to know what each symbol represents. Angular position, velocity, and acceleration are always represented using the symbols shown below
Displacement
Instead of s, which you use in linear travel, use
;
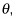The angular displacement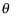 
is measured in radians.
Velocity
In place of the velocity, v, use the angular velocity,
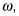
Angular velocity is the number of radians covered per second.
Acceleration
Instead of acceleration, a, use the angular acceleration,
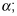
The unit for angular acceleration is radians per second2.
The table compares the formulas for both linear and angular motion.
For example, that you have a ball tied to a string. What’s the angular velocity of the ball if you whirl it around? It makes a complete circle,
In 0.5 seconds, so its angular velocity is
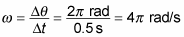
Another demonstration of the usefulness of radians in measuring angles is that the linear speed can easily be related to the angular speed. If you take the equation
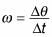
And multiply both sides by the radius, r, you get
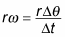
The term
Is simply the distance travelled by an object moving in a circle of radius r, so this equation becomes?
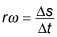
The kinetic energy of a rotating object is analogous to linear kinetic energy and can be expressed in terms of the moment of inertia and angular velocity. The total kinetic energy of an extended object can be expressed as the sum of the translational kinetic energy of the center of mass and the rotational kinetic energy about the center of mass. For a given fixed axis of rotation, the rotational kinetic energy can be expressed in the form
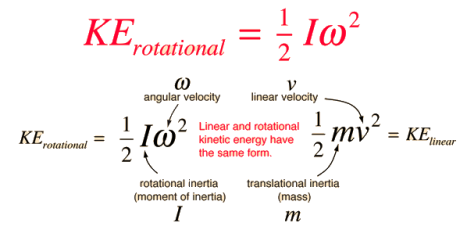
The expressions for rotational and linear kinetic energy can be developed in a parallel manner from the work-energy principle. Consider the following parallel between a constant torque exerted on a flywheel with moment of inertia I and a constant force exerted on a mass m, both starting from rest.
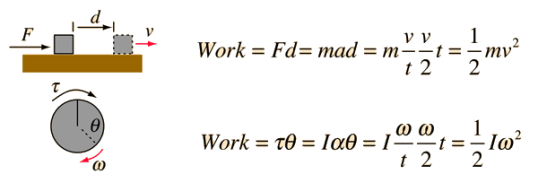
For the linear case, starting from rest, the acceleration from Newton's second law is equal to the final velocity divided by the time and the average velocity is half the final velocity, showing that the work done on the block gives it a kinetic energy equal to the work done.
For the rotational case, also starting from rest, the rotational work is τθ and the angular acceleration α given to the flywheel is obtained from Newton's second law for rotation. The angular acceleration is equal to the final angular velocity divided by the time and the average angular velocity is equal to half the final angular velocity. It follows that the rotational kinetic energy given to the flywheel is equal to the work done by the torque.
The moment of inertia of any object about an axis through its center of mass is the minimum moment of inertia for an axis in that direction in space. The moment of inertia about any axis parallel to that axis through the center of mass is given by
The expression added to the center of mass moment of inertia will be recognized as the moment of inertia of a point mass - the moment of inertia about a parallel axis is the center of mass moment plus the moment of inertia of the entire object treated as a point mass at the center of mass.
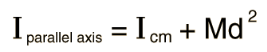
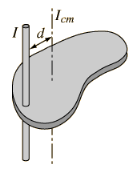
Since the moment of inertia of an ordinary object involves a continuous distribution of mass at a continually varying distance from any rotation axis, the calculation of moments of inertia generally involves calculus, the discipline of mathematics which can handle such continuous variables. Since the moment of inertia of a point mass is defined by
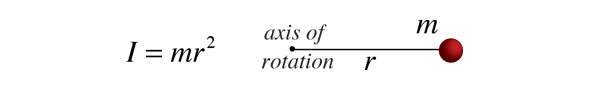
Then the moment of inertia contribution by an infinitesmal mass element dm has the same form. This kind of mass element is called a differential element of mass and its moment of inertia is given by
Note that the differential element of moment of inertia dI must always be defined with respect to a specific rotation axis. The sum over all these mass elements is called an integral over the mass.
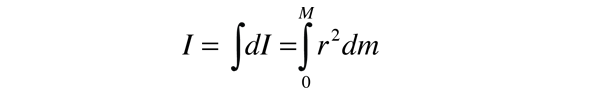
Usually, the mass element dm will be expressed in terms of the geometry of the object, so that the integration can be carried out over the object as a whole (for example, over a long uniform rod).
Moment of inertia is defined with respect to a specific rotation axis. The moment of inertia of a point mass with respect to an axis is defined as the product of the mass times the distance from the axis squared. The moment of inertia of any extended object is built up from that basic definition. The general form of the moment of inertia involves an integral.
The expression for the moment of inertia of a solid cylinder can be built up from the moment of inertia of thin cylindrical shells.
Using the general definition for moment of inertia:
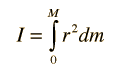
The mass element can be expressed in terms of an infinitesimal radial thickness dr by
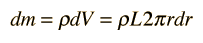
Substituting gives a polynomial form integral:
A body is said to satisfy the first condition for equilibrium if the resultant of all the forces acting on it is zero. Let n number of forces F1, F2, F3,……, Fn is acting on a body such that:
F1 +F2+F3+……+Fn =0
Or ∑ F =0 ……(1)
The symbol ∑ is a Greek letter called sigma used for summation. Equation (1) is called the first condition of equilibrium.
The first condition for equilibrium can also be stated in terms of X and Y components of the forces acting on the body as:
F1x +F2x+F3x+……+Fnx =0
And
F1y+F2y+F3y+……+Fny=0
Or
∑ Fx =0
∑ Fy=0
According to this, a body satisfies the second condition for equilibrium when the resultant torque acting on it is zero. Mathematically:
∑ τ =0
When a member is being loaded similar to that in figure one bending stress (or flexure stress) will result. Bending stress is a more specific type of normal stress. When a beam experiences load like that shown in figure one the top fibre of the beam undergo a normal compressive stress. The stress at the horizontal plane of the neutral is zero. The bottom fibres of the beam undergo a normal tensile stress. It can be concluded therefore that the value of the bending stress will vary linearly with distance from the neutral axis.
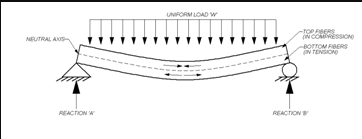
Normal stress is a result of load applied perpendicular to a member. Shear stress however results when a load is applied parallel to an area. Looking again at figure one, it can be seen that both bending and shear stresses will develop. Like in bending stress, shear stress will vary across the cross-sectional area.
Strain energy is defined as the energy stored in a body due to deformation. The strain energy per unit volume is known as strain energy density and the area under the stress-strain curve towards the point of deformation. When the applied force is released, the whole system returns to its original shape. It is usually denoted by U.
The strain energy formula is given as,
U = Fδ / 2
Where,
δ = compression,
F = force applied.
When stress σ is proportional to strain ϵ, the strain energy formula is given by,
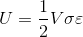
Where,
σ = stress
= strain
V = volume of body
Regarding Young’s modulus E, the strain energy formula is given as,
U = σ2 / 2E × V.
Where,
σ = stress,
E = Young’s modulus,
V = volume of body.
(Young Modulus)
If a metal bar of cross-sectional area A is pulled by a force F at each end, the bar stretches from its original length L0 to a new length Ln. (Simultaneously the cross section decreases.)
The stress is the quotient of the tensile force divided by the cross-sectional area, or F/A.
The strain or relative deformation is the change in length,
Ln − L0, divided by the original length, or (Ln − L0)/L0.
(Strain is dimensionless.)
Thus, Young’s modulus may be expressed mathematically as
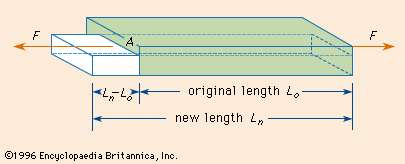
Young’s modulus = stress/strain = (FL0)/A(Ln − L0)
The units of Young’s modulus in the English system are pounds per square inch (psi),
And in the metric system newtons per square metre (N/m2).
The value of Young’s modulus for aluminium is about 1.0 × 107 psi, or 7.0 × 1010 N/m2. The value for steel is about three times greater, which means that it takes three times as much force to stretch a steel bar the same amount as a similarly shaped aluminium bar.
Objects deform when pushed, pulled, and twisted. Elasticity is the measure of the amount that the object can return to its original shape after these external forces and pressures stop.[2] This is what allows springs to store elastic potential energy.
The opposite of elasticity is plasticity; when something is stretched, and it stays stretched, the material is said to be plastic. When energy goes into changing the shape of some material and it stays changed, that is said to be plastic deformation. When the material goes back to its original form, that's elastic deformation
Mechanical energy is lost whenever an object undergoes plastic deformation. Manufacturing goods from raw materials involves a great deal of plastic deformation. For example, rolling steel into a particular shape (like rebar for construction) involves plastic deformation, since a new shape is created.
Most materials have an amount of force or pressure for which they deform elastically. If more force or pressure is applied, then they have plastic deformation. Materials that have a fair amount of plastic deformation before breaking are said to be ductile.[3] Materials that can't stretch or bend much without breaking are said to be brittle. Copper is quite ductile, which is part of why it is used for wires (most metals are ductile (but copper especially so). Glass and ceramics are often brittle; they will break rather than bend!
