Unit 1
Physical Quantities, Motion in Two or Three dimensions
A unit of measurement is some specific quantity that has been chosen as the standard against which other measurements of the same kind are made. For example, the meter (m) is the unit of measurement for length in the metric system. When an object is said to be 4 m long, that means that the object is four times as long as the unit standard (1 m).
The term standard refers to the physical object on which the unit of measurement is based. For example, for many years the standard used in measuring length in the metric system was the distance between two scratches on a platinum-iridium bar kept at the Bureau of Standards in Sèvres, France. A standard serve as a model against which other measuring devices of the same kind are made. The meter stick in a classroom or home is thought to be exactly 1 m long because it was made from a permanent model kept at the manufacturing plant that was originally copied from the standard meter in France.
All measurements consist of two parts: a scalar (numerical) quantity and the unit designation. In the measurement 8.5 m, the scalar quantity is 8.5 and the unit designation is meters.
ISQ Base Quantity | SI Base Unit |
Length | Meter (m) |
Mass | Kilogram (kg) |
Time | Second (s) |
Electrical current | Ampere (A) |
Thermodynamic temperature | Kelvin (K) |
Amount of substance | Mole (mol) |
Luminous intensity | Candela (cd) |
This is the fundamental apples and oranges'' rule. If I have six apples and seven oranges and add them together, I don't have thirteen apples, and I don't have thirteen oranges. Perhaps I have thirteen fruit, but if I do I should have written, and thought of, this as adding 6 fruit to 7 fruit. This is even more apparent if I subtract - who knows that subtracting two oranges from 6 apples even means? Adding two anti-oranges to the six apples?
This means that when we write:
 |
|
In (say) physics, 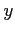 ,
, 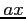 (as a product) and
(as a product) and 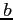 had better all have the same units and describe the same kind of physical quantity, or be dimensionless - pure numbers. This puts some obvious limitations on what you can do with algebraic transformation!
had better all have the same units and describe the same kind of physical quantity, or be dimensionless - pure numbers. This puts some obvious limitations on what you can do with algebraic transformation!
As we noted above, in most scientific disciplines, we use the same symbols over and over again to stand for different specific kinds of quantities that carry different kinds of units that are either implicit - assumed by convention if no units are given - or explicitly indicated in the problem. In physics, the units are usually the Standard International (SI) unit set, where e.g. a mass symbol such as 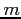 or
or 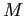 is in kilograms, a time symbol
is in kilograms, a time symbol 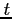 ,
, 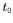 , or
, or 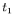 is in seconds, lengths like
is in seconds, lengths like 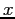 ,
, 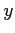 , or
, or 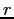 are in meters.
are in meters.
This means that expressions like 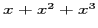 (the sum of a length, an area, and a volume) or
(the sum of a length, an area, and a volume) or 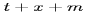 (the sum of a time, a length, a mass) are completely meaningless! Requiring consistency of units is a powerful (and additional) difference between ordinary math'' algebra and algebra used in application to the real world!
(the sum of a time, a length, a mass) are completely meaningless! Requiring consistency of units is a powerful (and additional) difference between ordinary math'' algebra and algebra used in application to the real world!
This actually is a great boon to those seeking to solve problems! You can take it as a given that physical laws are always dimensionally consistent. If you try to formulate and solve a problem using them and end up with things on two sides of an equal sign with different units or a sum on one side of an equal’s sign containing terms with different units, you can be absolutely certain that your answer is wrong and furthermore, that you made a mistake doing the algebra! This means that you can go back to the algebra and check and see where you multiplied where you should have divided or the like, and possibly solve the problem correctly.
Let’s consider a simple example of how to convert units. Suppose we want to convert 80 m to kilometers. The first thing to do is to list the units you have and the units to which you want to convert. In this case, we have units in meters and we want to convert to kilometers. Next, we need to determine a conversion factor relating meters to kilometers. A conversion factor is a ratio that expresses how many of one unit are equal to another unit. For example, there are 12 in. In 1 ft, 1609 m in 1 mi, 100 cm in 1 m, 60 s in 1 min, and so on. For a more complete list of conversion factors. In this case, we know that there are 1000 m in 1 km. Now we can set up our unit conversion.
Measurements may be accurate, meaning that the measured value is the same as the true value; they may be precise, meaning that multiple measurements give nearly identical values (i.e., reproducible results); they may be both accurate and precise; or they may be neither accurate nor precise. The goal of scientists is to obtain measured values that are both accurate and precise.
Suppose, for example, that the mass of a sample of gold was measured on one balance and found to be 1.896 g. On a different balance, the same sample was found to have a mass of 1.125 g. Which was correct? Careful and repeated measurements, including measurements on a calibrated third balance, showed the sample to have a mass of 1.895 g.
The masses obtained from the three balances are in the following table:

Whereas the measurements obtained from balances 1 and 3 are reproducible (precise) and are close to the accepted value (accurate), those obtained from balance 2 are neither. Even if the measurements obtained from balance 2 had been precise (if, for example, they had been 1.125, 1.124, and 1.125), they still would not have been accurate.
When scientists make a measurement or calculate some quantity from their data, they generally assume that some exact or "true value" exists based on how they define what is being measured (or calculated). Scientists reporting their results usually specify a range of values that they expect this "true value" to fall within. The most common way to show the range of values is:
Measurement = best estimate ± uncertainty
Experimental uncertainties should be rounded to one significant figure.
Wrong: 52.3 cm ± 4.1 cm
Correct: 52 cm ± 4 cm
Always round the experimental measurement or result to the same decimal place as the uncertainty
Wrong: 1.237 s ± 0.1 s
Correct: 1.2 s ± 0.1 s
It is important to be honest when reporting a measurement, so that it does not appear to be more accurate than the equipment used to make the measurement allows. We can achieve this by controlling the number of digits, or significant figures, used to report the measurement.
Determining the Number of Significant Figures
The number of significant figures in a measurement, such as 2.531, is equal to the number of digits that are known with some degree of confidence (2, 5, and 3) plus the last digit (1), which is an estimate or approximation. As we improve the sensitivity of the equipment used to make a measurement, the number of significant figures increases.
Postage Scale |
| 3 g |
| 1 significant figure |
Two-pan balance |
| 2.53 g |
| 3 significant figures |
Analytical balance |
| 2.531 |
| 4 significant figures |
Rules for counting significant figures are summarized below.
Zeros within a number are always significant. Both 4308 and 40.05 contain four significant figures.
Zeros that do nothing but set the decimal point are not significant. Thus, 470,000 has two significant figures.
Trailing zeros that aren't needed to hold the decimal point are significant. For example, 4.00 has three significant figures.
If you are not sure whether a digit is significant, assume that it isn't. For example, if the directions for an experiment read: "Add the sample to 400 mL of water," assume the volume of water is known to one significant figure.
Addition and Subtraction with Significant Figures
When combining measurements with different degrees of accuracy and precision, the accuracy of the final answer can be no greater than the least accurate measurement. This principle can be translated into a simple rule for addition and subtraction: When measurements are added or subtracted, the answer can contain no more decimal places than the least accurate measurement.
150.0 g H2O | (using significant figures) |
+ 0.507 g salt | |
150.5 g solution | |
Multiplication and Division with Significant Figures
The same principle governs the use of significant figures in multiplication and division: the final result can be no more accurate than the least accurate measurement. In this case, however, we count the significant figures in each measurement, not the number of decimal places: When measurements are multiplied or divided, the answer can contain no more significant figures than the least accurate measurement.
Example: To illustrate this rule, let's calculate the cost of the copper in an old penny that is pure copper. Let's assume that the penny has a mass of 2.531 grams, that it is essentially pure copper, and that the price of copper is 67 cents per pound. We can start by from grams to pounds.
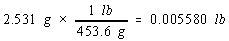
We then use the price of a pound of copper to calculate the cost of the copper metal.

Order of magnitude is the quantity of powers of 10 that there are in a number, or the number of powers of 0.1 in a negative number. Order of magnitude is usually written as 10 to the nth power. The n represents the order of magnitude. If you raise a number by one order of magnitude, you are basically multiplying that number by 10. If you decrease a number by one order of magnitude, you are basically multiplying that number by 0.1.
Estimation means using prior experience and sound physical reasoning to arrive at a rough idea of a quantity’s value. Because the process of determining a reliable approximation usually involves the identification of correct physical principles and a good guess about the relevant variables, estimating is very useful in developing physical intuition. Estimates also allow us perform “sanity checks” on calculations or policy proposals by helping us rule out certain scenarios or unrealistic numbers. They allow us to challenge others (as well as ourselves) in our efforts to learn truths about the world.
Many estimates are based on formulas in which the input quantities are known only to a limited precision. As you develop physics problem-solving skills (which are applicable to a wide variety of fields), you also will develop skills at estimating. You develop these skills by thinking more quantitatively and by being willing to take risks.
To describe motion in two and three dimensions, we must first establish a coordinate system and a convention for the axes. We generally use the coordinates x, y, and z to locate a particle at point P (x, y, z) in three dimensions. If the particle is moving, the variables x, y, and z are functions of time (t):
x=x(t) y=y(t) z=z(t).
The position vector from the origin of the coordinate system to point P is r⃗ (t). In unit vector notation, introduced in Coordinate Systems and Components of a Vector, r⃗ (t) is
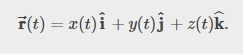
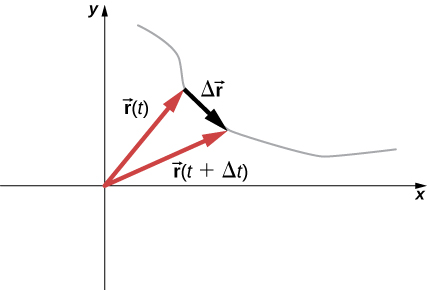
The instantaneous velocity vector is now
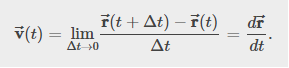
Let’s look at the relative orientation of the position vector and velocity vector graphically. We show the vectors r⃗ (t)and r⃗ (t+Δt) which give the position of a particle moving along a path represented by the Gray line. As Δt goes to zero, the velocity vector, becomes tangent to the path of the particle at time t.
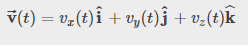
Where
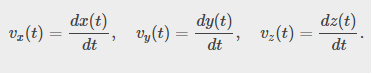
Acceleration vector at any point in time along its trajectory. This acceleration vector is the instantaneous acceleration and it can be obtained from the derivative with respect to time of the velocity function, as we have seen in a previous chapter. The only difference in two or three dimensions is that these are now vector quantities. Taking the derivative with respect to time →v(t),v→(t), we find
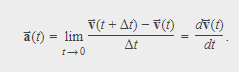
The acceleration in terms of components is
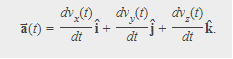
Also, since the velocity is the derivative of the position function, we can write the acceleration in terms of the second derivative of the position function:
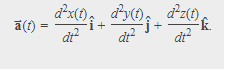
When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion. Air resistance to the motion of the body is to be assumed absent in projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
- Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle.
- Along y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle.
Accelerations in the horizontal projectile motion and vertical projectile motion of a particle: When a particle is projected in the air with some speed, the only force acting on it during its time in the air is the acceleration due to gravity (g). This acceleration acts vertically downward. There is no acceleration in the horizontal direction, which means that the velocity of the particle in the horizontal direction remains constant.
Parabolic Motion of Projectiles
Let us consider a ball projected at an angle θ with respect to the horizontal x-axis with the initial velocity u as shown below:
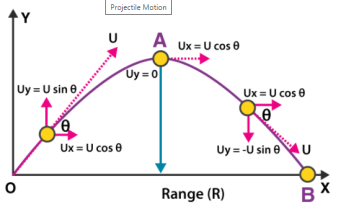
The point O is called the point of projection; θ is the angle of projection and OB = Horizontal Range or Simply Range. The total time taken by the particle from reaching O to B is called the time of flight.
For finding different parameters related to projectile motion, we can make use of differential equations of motions:
Total Time of Flight:
Resultant displacement (s) = 0 in Vertical direction. Therefore, by using the Equation of motion:
i.e. gt2 = 2t × u sin θ
Therefore, the total time of flight (t):

Horizontal Range:
Horizontal Range (OA) = Horizontal component of velocity (ux) × Total Flight Time (t)
R = u cos θ × 2u×sinθg
Therefore, in a projectile motion the Horizontal Range is given by (R):

Maximum Height:
It is the highest point of the trajectory (point A). When the ball is at point A, the vertical component of the velocity will be zero. i.e. 0 = (u sin θ)2 – 2g Hmax [s = Hmax , v = 0 and u = u sin θ]
Therefore, in projectile motion, the Maximum Height is given by (Hmax):
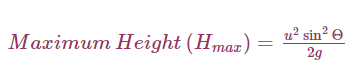
The equation of Trajectory:
Let, the position of the ball at any instant (t) be M (x, y). Now, from Equations of Motion:
x = t × u cos θ . . . . . . (1)
y = u sin θ × t – 12×t2g . . (2)
On substituting Equation (1) in Equation (2):

This is the Equation of Trajectory in projectile motion, and it proves that the projectile motion is always parabolic in nature.
Circular motion is the motion of a body following a circular path. Uniform circular motion is a specific type of circular motion in which the motion of a body following a circular path is at a constant speed. The body has a fixed central point and remains equidistant from it at any given position.
When an object goes around in a circle, the description of its motion becomes interesting in many ways. To better understand the circular motion let us look at an example.
Suppose you have a ball attached to a string and you move it constantly in a circular motion. Then we observe two things:
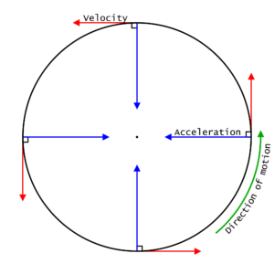
- The speed of the ball is constant. It traces a circle with a fixed centre.
- At every point of its motion, the ball changes its direction. Therefore, we can say that in order to stay on a circular path, the ball has to change its direction continuously.
Newton’s first law of motion tells us that there can be no acceleration without a net force. So, there must be a force associated with the circular motion. In other words, for the circular motion to take place a net force has to act on the object. Thus, the change in direction is a result of a centripetal force.
As long as the ball is attached to the string, it will continue to follow the circular path. The moment the string breaks or you let go of the string, the centripetal force stops acting and the ball flies away.
The relative velocity is the velocity of an object or observer B in the rest frame of another object or the observer A. The general formula of velocity is:
 ,
,
This is the only formula that describes the concept of relative velocity. When two objects are moving in the same direction, then
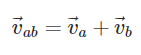
When two objects are moving in the opposite direction, then
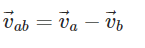
Consider two trains moving with same speed and in the same direction. Even if both the trains are in motion with respect to buildings, trees along the two sides of the track, yet to the observer of the train, the other train does not seem to be moving at all. The velocity of the other train appears to be zero.
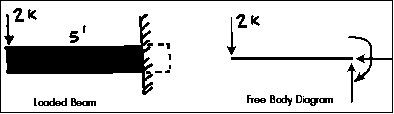
One of the most useful aids for solving a statics problem is the free body diagram (FBD). A free body diagram is a graphic, dematerialized, symbolic representation of the body (structure, element or segment of an element) in which all connecting "pieces" have been removed. A FBD is a convenient method to model the structure, structural element, or segment that is under scrutiny. It is a way in which to conceptualize the structure, and its composite elements, so that an analysis may be initialized.
All of the physical attributes of the structure are removed. This is not completed at random, rather with a distinct method. A body, or segment thereof, is represented by a simple single line. Each connection is solely represented by a juncture with distinct properties, or is replaced by a set of forces and moments which would represent the action at that connection. Internal forces which would be found at a node (connection or joint) can be replaced by representational external forces where that "part" connects would connect with the other member in the FBD. All loads are represented as force systems.
Everything that is needed to solve a force system is included on the FBD. Free body diagrams may not seem necessary in the relatively simple current applications, but as problems become more complex, their usefulness increases.

Conservative Forces:
Conservative forces are those for which work done depends only on initial and final points.
For example, Gravitational Force, Electrostatic Force
Non-Conservative Forces:
Non-Conservative forces are those where the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object.
For example, Frictional Force

A force is said to be central under two conditions.
First, the direction of the force must always be toward or away from a fixed point. This point is known as the centre of the force.
Second, the magnitude of the force should only be proportional to the distance r between the particle and the centre of the force. The central force may be written as
F=f(r)r1
Where r1r1 is a unit vector in the direction of r. Therefore, if f(r)<0 then the central force is an attractive force since it is directed toward the centre of the force O and if f(r)>0f, the force is repulsively directed away from O.
Properties of a Central Force
The resulting motion of the particle takes place in a plane. To show that we have from

Where h is a constant vector. Therefore, r and v always lie in the same plane where h is perpendicular to that plane for every value of t. As a result, the path of the particle takes place in a plane
The angular momentum of the particle is conserved., we have
m(r×v) =mh
Or
L=mh=constant
The position vector r of the particle with respect to the centre of force sweeps out equal areas in equal times or in other words, the areal velocity is constant. To show that, consider the plane of motion to be the x–y plane. During an infinitesimally small-time interval dt, the radius vector r sweeps out an area equal to dA. This area is equal to half of the area of a parallelogram with sides r and dr. That is,
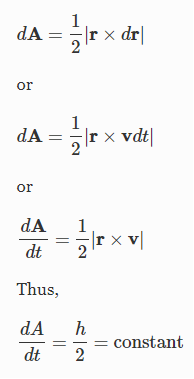
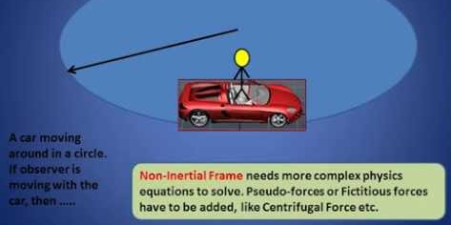
Now we can define a non-inertial frame as a frame that is accelerated with respect to the assumed inertial frame of reference. Newton’s law will not hold true in these frames. So, in the above example if I assume earth to be an inertial reference frame the moon becomes a non-inertial reference frame as it is in accelerated motion with respect to earth. But if we want to make Newton’s law hold here, we need to take some mysterious forces also known as pseudo forces
Non−inertial reference frame is a reference frame that is accelerating either in linear fashion or rotating around some axis.
Examples: − inertial references frames − A train moving with constant velocity.
Non−inertial references frames− A turning car with constant speed