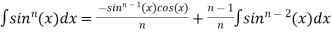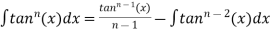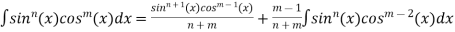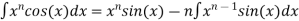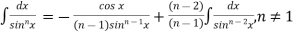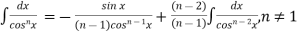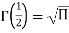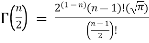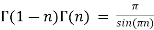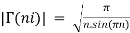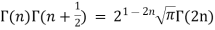UNIT-1
1.1Evaluation of definite and improper integrals.
An improper integral is a definite integral—one with upper and lower limits—that goes to infinity in one direction or another. Either one of its limits are infinity, or the integrand (that function inside the interval, usually represented by f(x)) goes to infinity in the integral.
Improper integrals are integrals you can’t immediately solve because of the infinite limit(s) or vertical asymptote in the interval. The reason you can’t solve these integrals without first turning them into a proper integral (i.e. one without infinity) is that in order to integrate, you need to know the interval length. And if your interval length is infinity, there’s no way to determine that interval. The workaround is to turn the improper integral into a proper one and then integrate by turning the integral into a limit problem.
Example1: Solve the following improper Integral
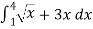
Solution:
Given, 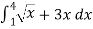
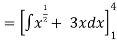
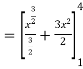
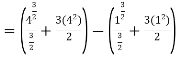
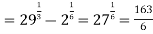
Example 2: Solve the following improper Integral
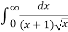
Solution: Given,
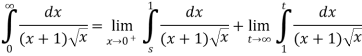
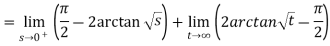
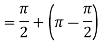
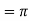
Example 3: Solve the following improper Integral
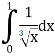
Solution: Given,
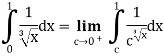
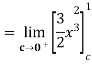
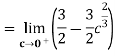
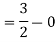

Example 4 : Solve the following improper Integral
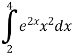
Solution: Given,
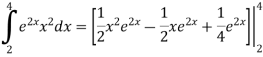
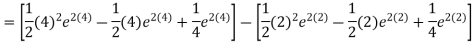
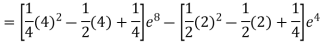
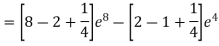

Reduction formula is regarded as a method of integration. Integration by reduction formula helps to solve the powers of elementary functions, polynomials of arbitrary degree, products of transcendental functions and the functions that cannot be integrated easily, thus, easing the process of integration and its problems.
Reduction Formula for Exponential Functions
∫xn emx dx = [(1/m) xnemx ]− [(n/m) ∫xn−1 emx ]dx
∫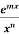 dx = − [
dx = − [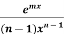 ]+ [(
]+ [(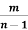 ) ∫
) ∫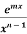 dx, n≠1
dx, n≠1
Reduction Formula for Hyperbolic Trigonometric Functions
- ∫sinhnx dx = −
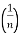 sinhn−1 x cosh x −
sinhn−1 x cosh x − 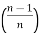 ∫sinhn−2x dx
∫sinhn−2x dx - ∫coshnx dx =
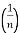 sinhx coshn−1 x −
sinhx coshn−1 x − 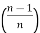 ∫coshn−2x dx
∫coshn−2x dx - ∫tanhnx dx = −
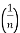 tanhn−1x + ∫tanhn−2x dx, n≠1
tanhn−1x + ∫tanhn−2x dx, n≠1 - ∫cothnx dx = −
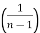 cothn−1x + ∫cothn−2x dx, n≠1
cothn−1x + ∫cothn−2x dx, n≠1 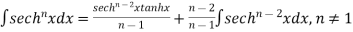
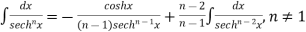

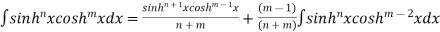
Reduction formulae for Trigonometric Functions
Reduction Formula for Logarithmic Functions:
Example 1: evaluate the integral 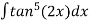
Solution: we use 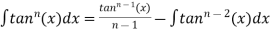
Substituting a=2x
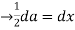
Hence,
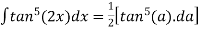
= 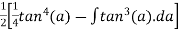
=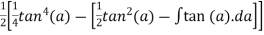
= 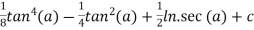
= 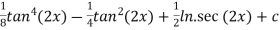
Example2: evaluate the integral 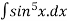
Solution: we use the formula 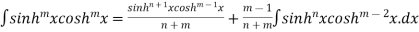
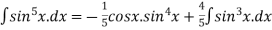
= 
= 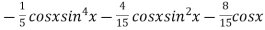 .
.
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral
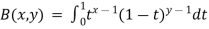
For complex number inputs x, y such that Re x > 0, Re y > 0.
Gamma properties:
Beta properties:
 (m, n) = B (n, m)
(m, n) = B (n, m) (m, n) =
(m, n) = 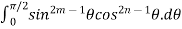
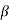 (m, n) =
(m, n) = 
 (m, n) =
(m, n) = 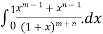
Relation between beta and gamma function is defined by:
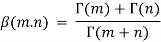
Example 1: f(B) = 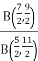 Solve the given function.
Solve the given function.
Solution: 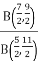 =
= 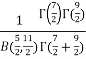
= 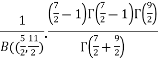 [Recursive function for the gamma function]
[Recursive function for the gamma function]
=  [Recursive formula for the gamma function]
[Recursive formula for the gamma function]
=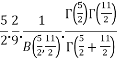
=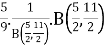 [By the definition of Beta function]
[By the definition of Beta function]
= 
Example 2: B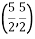 =
=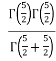
= 
= 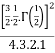
=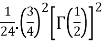
= 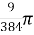 [because
[because  ]
]
Example 1: Find the area of the surface generated by rotating the function about the x-axis over
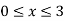 and the curve
and the curve 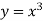
Solution: we have the equation of the form y=f(x) and we are rotating around the x-axis, we’ll use the formula
S = 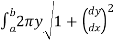
We will calculate 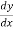 and then substitute it back into the equation
and then substitute it back into the equation
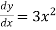
S = 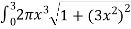
S =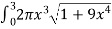
Using u-substitution and setting u= 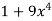 and du=36x3dx,
and du=36x3dx,
We calculate

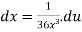
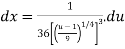
Plugging these values back into the integral we get,
S= 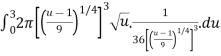
S = 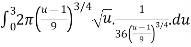
S = 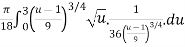
S = 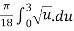
By integration we get
S = 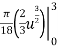
S =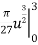
We will insert back for u, and we have u = 1+9x4, and then evaluate over the interval
S = 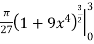
= 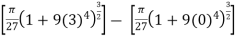
S = 2, 294.8 square units.
THEREFORE,
The surface area obtained by rotating y= x3 around the x-axis over the interval 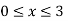 is S = 2, 294.8
is S = 2, 294.8
Example 2: Find the volume generated by revolving the region bounded by y = x2 and the x-axis on [-2,3] about the x-axis
Solution: The volume(v) of the solid is
V = 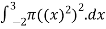
= 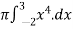
= 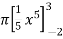
= 
V = 55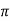 .
.