Unit – 6
Infinite Series
A sequence is a list of numbers in a special order. It is a string of numbers following a particular pattern, and all the elements of a sequence are called its terms. Let us consider a sequence,
[1, 3, 5, 7, 9, 11……]
We can say this is sequence because we know that they are the collection of odd natural numbers. Here the number of terms in the sequence will be infinite. Such a sequence which contains the infinite number of terms is known as an infinite sequence. But what if we put end to this.
[1, 3, 5, 7, 9, 11…..131]
If 131 is the last term of this sequence, we can say that the number of terms in this sequence is countable. So in such a sequence in which the number of terms is countable, they are called finite sequences. A finite sequence has a finite number of terms. So as discussed earlier here 1 is the term, 3 is the term so is 5, 7, …..
Fibonacci Sequence
The special thing about the Fibonacci sequence is that the first two terms are fixed. When we talk about the terms, there is a general representation of these terms in sequences and series. A term is usually denoted as an here ‘ n ‘ is the nth term of a sequence. For the Fibonacci sequence, the first two terms are fixed.
The first term is as a1= 1 and a2= 1. Now from the third term onwards, every term of this Fibonacci sequence will become the sum of the previous two terms. So a3 will be given as a1 + a2
Therefore, 1 + 1 = 2. Similarly,
a4 = a2 + a3
∴ 1 + 2 = 3
a5 = a3+ a4
∴ 2 + 3 = 5
Therefore if we want to write the Fibonacci sequence, we will write it as,
[1 1 2 3 5…]. So, in general, we can say,
an = an-1 + an-2
Where the value of n ≥ 3.
Types of Sequences
- Arithmetic sequence: In an arithmetic (linear) sequence the difference between any two consecutive terms is constant.
- Quadratic Sequence: A quadratic sequence is a sequence of numbers in which the second difference between any two consecutive terms is constant.
- Geometric Sequence: A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
Series
Series is the sum of sequences. The series is finite or infinite according to the given sequence is finite or infinite. Series are represented as sigma, which indicates that the summation is involved. For example, a series S can be,
S = Sum (1, 3, 5, 7, 9, 11, …)
Example:
Identify the sequence of the following function n (n+3)
- 4, 10, 26, …
- 4, 12, 18, …
- 2, 10, 16, …
- 4, 10, 27, …
Solution: Correct option is A. The given function is n(n+3),
When n = 1, 1(1+3) = 4
n = 2, 2(2+3) = 10
n=3, 3(3+3) = 27
So, 4, 10, 27…is the function for the sequence n(n+3).
Example 2:
Question: Adding first 100 terms in a sequence is
- Term
- Series
- Constant
- Sequence
Solution: Correct option is B. Adding first 100 terms in a sequence is series. Also adding the number of some set is a series.
A series 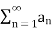 is said to Converge to the sum s if the sequence of partial
is said to Converge to the sum s if the sequence of partial
Sums (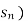
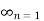 = 1 converges to s, i.e.,
= 1 converges to s, i.e., 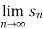 =s.
=s.
A series is said to Diverge if it does not converge to any sum.
*If the sum of the series is finite then the series is convergent.
Ie., 1 - 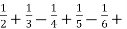 .........
.........
* If the sum of the series is finite then the series is divergent.
Ie., 1+2+4+8+16+...........
*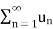 =
=  diverges.
diverges.
*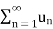 = a , converges.
= a , converges.
Example 1:
Determine whether the following series converges or diverges
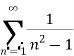
Solution:
Consider the given series ie., 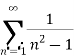
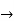
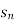 =
= 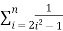 =
= -
-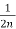 -
-
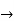
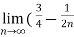 -
-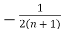 ) =
) = 
Since ,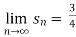
 therefore the given series is convergent.
therefore the given series is convergent.
Example 2:
Determine whether the following series is divergent or convergent

Solution:
Given,
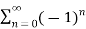
 s0 =1
s0 =1
 s1 = 1-1=0
s1 = 1-1=0
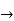 s2 = 1-1+1=1
s2 = 1-1+1=1
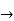 s3 = 1-1+1-1=0
s3 = 1-1+1-1=0
Hence the series diverges since 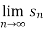 doesn’t exist.
doesn’t exist.
A necessary and sufficient condition is established which ensures the strong convergence of the steepest descent approximation to a solution of equations involving quasi-accretive operators defined on a uniformly smooth Banach space.
Let ak be a sequence of real numbers. Let An be a sequence of partial sums of
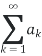
If , 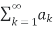 converges (i.e. An converges), then
converges (i.e. An converges), then
(a) 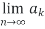 =0 converges.
=0 converges.
(b) An is bounded.
In other words, (a) and (b) are necessary conditions for the convergence of a series.
Example 1:
Given 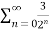 =
=  n
n
= 3(1)+3( ) +3(
) +3( )2 +.........
)2 +.........
Has a ratio of r=  with a=3
with a=3
As 0< 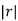 <1, the series converges and the sum is
<1, the series converges and the sum is
S=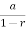 =
=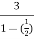 =6.
=6.
Example 2:
Solve the following geometric series,
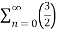 n =1+
n =1+  +
+ +
+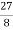 +........
+........
Gives a ratio of r=
Because 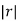
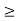 1, the series diverges.
1, the series diverges.
p-series test:
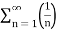 p =
p =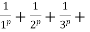 .........
.........
Converges , if p>1
Diverges, if p<1
Example 1:
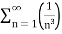 =
= 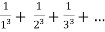
Here p = 3 so p>1 ,thus the given series converges.
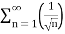 =
= 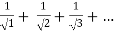
Here p= ie., p<1,thus the given series diverges
ie., p<1,thus the given series diverges
Example 2:
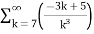
= 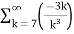 +
+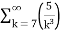
= -3.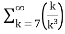 +5.
+5.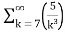
=-3.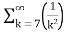 +5.
+5.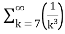
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges.
Comparison test:
- If the infinite series
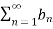 converges and 0≤
converges and 0≤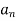 ≤
≤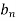 ,for all n>N,
,for all n>N,
Where N is some fixed number, then 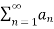 also converges.
also converges.
- If the infinite series
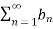 diverges and 0≤
diverges and 0≤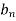 ≤
≤ ,for all n>N,
,for all n>N,
Where N is some fixed number, then 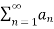 also diverges.
also diverges.
Example 1:
Find whether the following series is convergent or divergent?

Solution:
=  <
< 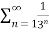 =
= 
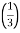 n-1 <
n-1 <
So the series converges
Example 2:
 .dx ., test for convergence
.dx ., test for convergence
Solution :
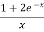 >
> 
Hence the series diverges
Ratio test:
To test convergence of ratio test we follow the below method,
Consider,
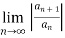 = L
= L
If L<1 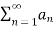 is absolutely convergent
is absolutely convergent
If L > 1 or 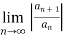 =
=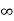 then
then 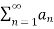 is divergent
is divergent
If L=1 then the series is inconclusive.
Example 1:
L = 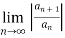
=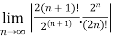
= 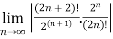
= 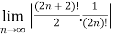
= 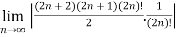
=
=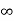
Example 2:

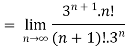
=
= 0
Therefore the series converges since, 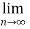 is 0.
is 0.
Nth root test:
If 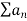 is a series with positive terms and
is a series with positive terms and 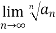 =L then,
=L then,
The series converges if L < 1
The series diverges if L>1
The test is in conclusive if L=1
Note : These rules are same for ratio test.
Example 1:
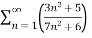 n=
n= 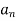
=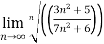 n =
n = 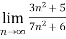 =
= <1
<1
Therefore the series is convergent by root test.
Example 2:
L= 
= 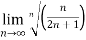 n
n
= 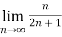
= ½
Therefore the series is convergent
Leibnitz test:
Leibnitz test is an alternative way of expressing derivatives to ff’(x),g’(x),etc.,
If y is expressed in terms of x then the derivative is written as 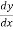
Example 1:
Y = 3x2 – 7x
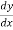 = 6x-7
= 6x-7
Example 2:
Q = 9R2- 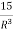 to find
to find 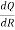
Solution:
Q = 9R2-15R-3
Now,
 = 18R+45R-2 = 18R +
= 18R+45R-2 = 18R +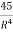
Power series:
A power series can be written in the form of
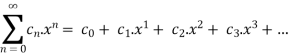
It can be written in the form of a function as.,
f(x) =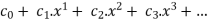
If we let 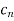 =1 for all n then the power series tends to geometric series
=1 for all n then the power series tends to geometric series
f(x) = 1+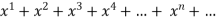
The above series converges if -1<x<1
The above series diverges if x≥ 1 and x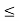 -1
-1
Example:
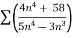 n
n
L= 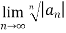 =
= 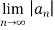 1/n
1/n
L= 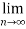
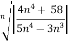 n =
n =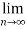

=  <1
<1
Hence the series converges.
Taylor series:
The Taylor’s series can be represented as the following
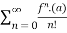 (x-a)n
(x-a)n
Example 1:
Find the Taylor series for the following:
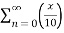
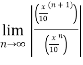 =
= 
 <1
<1
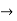 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
 ROC =10
ROC =10
Example 2:
f(n)5 = 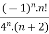
Here the ROC is 4
McLaurin series:
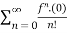 (x)n
(x)n
Example:
f(x)=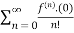
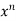
= f(0)+f’(0)x+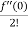 x2 +
x2 +  x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 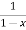
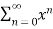
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson
Unit – 6
Infinite Series
A sequence is a list of numbers in a special order. It is a string of numbers following a particular pattern, and all the elements of a sequence are called its terms. Let us consider a sequence,
[1, 3, 5, 7, 9, 11……]
We can say this is sequence because we know that they are the collection of odd natural numbers. Here the number of terms in the sequence will be infinite. Such a sequence which contains the infinite number of terms is known as an infinite sequence. But what if we put end to this.
[1, 3, 5, 7, 9, 11…..131]
If 131 is the last term of this sequence, we can say that the number of terms in this sequence is countable. So in such a sequence in which the number of terms is countable, they are called finite sequences. A finite sequence has a finite number of terms. So as discussed earlier here 1 is the term, 3 is the term so is 5, 7, …..
Fibonacci Sequence
The special thing about the Fibonacci sequence is that the first two terms are fixed. When we talk about the terms, there is a general representation of these terms in sequences and series. A term is usually denoted as an here ‘ n ‘ is the nth term of a sequence. For the Fibonacci sequence, the first two terms are fixed.
The first term is as a1= 1 and a2= 1. Now from the third term onwards, every term of this Fibonacci sequence will become the sum of the previous two terms. So a3 will be given as a1 + a2
Therefore, 1 + 1 = 2. Similarly,
a4 = a2 + a3
∴ 1 + 2 = 3
a5 = a3+ a4
∴ 2 + 3 = 5
Therefore if we want to write the Fibonacci sequence, we will write it as,
[1 1 2 3 5…]. So, in general, we can say,
an = an-1 + an-2
Where the value of n ≥ 3.
Types of Sequences
- Arithmetic sequence: In an arithmetic (linear) sequence the difference between any two consecutive terms is constant.
- Quadratic Sequence: A quadratic sequence is a sequence of numbers in which the second difference between any two consecutive terms is constant.
- Geometric Sequence: A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
Series
Series is the sum of sequences. The series is finite or infinite according to the given sequence is finite or infinite. Series are represented as sigma, which indicates that the summation is involved. For example, a series S can be,
S = Sum (1, 3, 5, 7, 9, 11, …)
Example:
Identify the sequence of the following function n (n+3)
- 4, 10, 26, …
- 4, 12, 18, …
- 2, 10, 16, …
- 4, 10, 27, …
Solution: Correct option is A. The given function is n(n+3),
When n = 1, 1(1+3) = 4
n = 2, 2(2+3) = 10
n=3, 3(3+3) = 27
So, 4, 10, 27…is the function for the sequence n(n+3).
Example 2:
Question: Adding first 100 terms in a sequence is
- Term
- Series
- Constant
- Sequence
Solution: Correct option is B. Adding first 100 terms in a sequence is series. Also adding the number of some set is a series.
A series 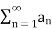 is said to Converge to the sum s if the sequence of partial
is said to Converge to the sum s if the sequence of partial
Sums (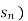
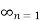 = 1 converges to s, i.e.,
= 1 converges to s, i.e., 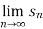 =s.
=s.
A series is said to Diverge if it does not converge to any sum.
*If the sum of the series is finite then the series is convergent.
Ie., 1 - 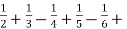 .........
.........
* If the sum of the series is finite then the series is divergent.
Ie., 1+2+4+8+16+...........
*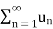 =
=  diverges.
diverges.
*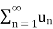 = a , converges.
= a , converges.
Example 1:
Determine whether the following series converges or diverges
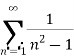
Solution:
Consider the given series ie., 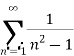
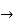
 =
= 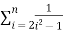 =
= -
-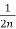 -
-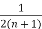
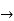
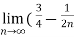 -
-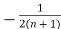 ) =
) = 
Since ,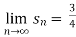
 therefore the given series is convergent.
therefore the given series is convergent.
Example 2:
Determine whether the following series is divergent or convergent

Solution:
Given,
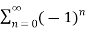
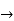 s0 =1
s0 =1
 s1 = 1-1=0
s1 = 1-1=0
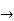 s2 = 1-1+1=1
s2 = 1-1+1=1
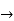 s3 = 1-1+1-1=0
s3 = 1-1+1-1=0
Hence the series diverges since 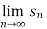 doesn’t exist.
doesn’t exist.
A necessary and sufficient condition is established which ensures the strong convergence of the steepest descent approximation to a solution of equations involving quasi-accretive operators defined on a uniformly smooth Banach space.
Let ak be a sequence of real numbers. Let An be a sequence of partial sums of
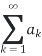
If , 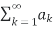 converges (i.e. An converges), then
converges (i.e. An converges), then
(a)  =0 converges.
=0 converges.
(b) An is bounded.
In other words, (a) and (b) are necessary conditions for the convergence of a series.
Example 1:
Given 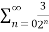 =
= 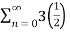 n
n
= 3(1)+3( ) +3(
) +3( )2 +.........
)2 +.........
Has a ratio of r=  with a=3
with a=3
As 0< 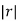 <1, the series converges and the sum is
<1, the series converges and the sum is
S=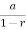 =
=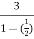 =6.
=6.
Example 2:
Solve the following geometric series,
 n =1+
n =1+  +
+ +
+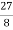 +........
+........
Gives a ratio of r=
Because 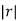
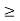 1, the series diverges.
1, the series diverges.
p-series test:
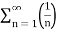 p =
p =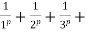 .........
.........
Converges , if p>1
Diverges, if p<1
Example 1:
 =
= 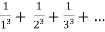
Here p = 3 so p>1 ,thus the given series converges.
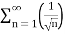 =
= 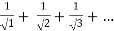
Here p= ie., p<1,thus the given series diverges
ie., p<1,thus the given series diverges
Example 2:
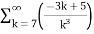
= 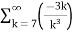 +
+
= -3.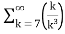 +5.
+5.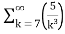
=-3.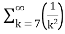 +5.
+5.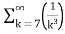
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges.
Comparison test:
- If the infinite series
 converges and 0≤
converges and 0≤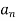 ≤
≤ ,for all n>N,
,for all n>N,
Where N is some fixed number, then 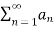 also converges.
also converges.
- If the infinite series
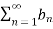 diverges and 0≤
diverges and 0≤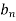 ≤
≤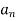 ,for all n>N,
,for all n>N,
Where N is some fixed number, then 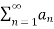 also diverges.
also diverges.
Example 1:
Find whether the following series is convergent or divergent?

Solution:
= 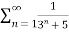 <
<  =
= 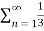
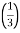 n-1 <
n-1 <
So the series converges
Example 2:
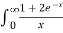 .dx ., test for convergence
.dx ., test for convergence
Solution :
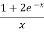 >
> 
Hence the series diverges
Ratio test:
To test convergence of ratio test we follow the below method,
Consider,
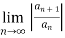 = L
= L
If L<1  is absolutely convergent
is absolutely convergent
If L > 1 or 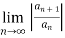 =
=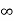 then
then  is divergent
is divergent
If L=1 then the series is inconclusive.
Example 1:
L = 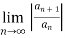
=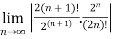
= 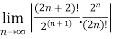
= 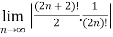
= 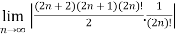
=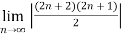
=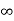
Example 2:
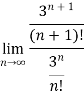
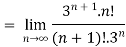
=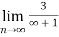
= 0
Therefore the series converges since, 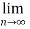 is 0.
is 0.
Nth root test:
If 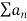 is a series with positive terms and
is a series with positive terms and 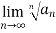 =L then,
=L then,
The series converges if L < 1
The series diverges if L>1
The test is in conclusive if L=1
Note : These rules are same for ratio test.
Example 1:
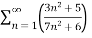 n=
n= 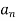
=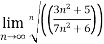 n =
n = 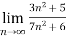 =
= <1
<1
Therefore the series is convergent by root test.
Example 2:
L= 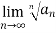
= 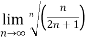 n
n
= 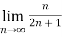
= ½
Therefore the series is convergent
Leibnitz test:
Leibnitz test is an alternative way of expressing derivatives to ff’(x),g’(x),etc.,
If y is expressed in terms of x then the derivative is written as 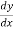
Example 1:
Y = 3x2 – 7x
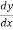 = 6x-7
= 6x-7
Example 2:
Q = 9R2- 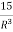 to find
to find 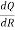
Solution:
Q = 9R2-15R-3
Now,
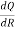 = 18R+45R-2 = 18R +
= 18R+45R-2 = 18R +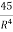
Power series:
A power series can be written in the form of

It can be written in the form of a function as.,
f(x) =
If we let 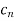 =1 for all n then the power series tends to geometric series
=1 for all n then the power series tends to geometric series
f(x) = 1+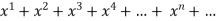
The above series converges if -1<x<1
The above series diverges if x≥ 1 and x -1
-1
Example:
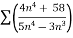 n
n
L= 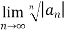 =
= 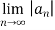 1/n
1/n
L= 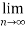
 n =
n =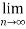
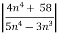
=  <1
<1
Hence the series converges.
Taylor series:
The Taylor’s series can be represented as the following
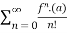 (x-a)n
(x-a)n
Example 1:
Find the Taylor series for the following:
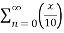
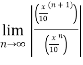 =
= 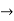
 <1
<1
 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
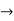 ROC =10
ROC =10
Example 2:
f(n)5 = 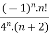
Here the ROC is 4
McLaurin series:
 (x)n
(x)n
Example:
f(x)=
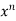
= f(0)+f’(0)x+ x2 +
x2 + 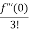 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 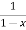
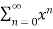
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson