Unit - 5
Algebra of Complex numbers and Roots of polynomial Equations
Geometric representation of complex numbers
With complex numbers, operations can also be represented geometrically. With the geometric representation of the complex numbers we can recognize new connections, which make it possible to solve further questions.
The complex plane (Gaussian plane)
Complex numbers are defined as numbers in the form z=a+ib or z=a+bi, where i is the imaginary part and a and b are real numbers. A complex number z is thus uniquely determined by the numbers (a,b)(a,b).
The geometric representation of complex numbers is defined as follows
A complex number z=a+ib z=a+ib is assigned the point (a,b)(a,b) in the complex plane. The complex plane is similar to the Cartesian coordinate system, it differs from that in the name of the axes.
The x-axis represents the real part of the complex number. This axis is called real axis and is labelled as Rℝ or Re
The y-axis represents the imaginary part of the complex number. This axis is called imaginary axis and is labelled with iR or Im
The origin of the coordinates is called zero point.
On the complex plane, the number 1 is a unit to the right of the zero point on the real axis and the Number ii is a unit above the zero point on the imaginary axis.
The complex numbers can be represented by points on a two-dimensional Cartesian coordinate system called the complex plane. In this way we establish a one to one correspondence between the set of all complex numbers and the set of all points in the plane. The set of all real numbers corresponds to the real axis x and the set of all purely imaginary numbers corresponds to the imaginary axis y
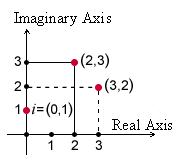
The Cartesian representation of the complex numbers specifies a unique point on the complex plane, and a given point has a unique Cartesian representation of the complex numbers.
Algebraic Operations on Complex Numbers
There can be four types of algebraic operation on complex numbers which are mentioned below. Visit the linked article to know more about these algebraic operations along with solved examples. The four operations on the complex numbers include:
- Addition
- Subtraction
- Multiplication
- Division
Roots of Complex Numbers
When we solve a quadratic equation in the form of ax2 +bx+c = 0, the roots of the equations can be determined in three forms;
- Two Distinct Real Roots
- Similar Root
- No Real roots (Complex Roots)
Complex Number Formulas
While performing the arithmetic operations of complex numbers such as addition and subtraction, combine similar terms. It means that combine the real number with the real number and imaginary number with the imaginary number.
Addition
(a + ib) + (c + id) = (a + c) + i(b + d)
Subtraction
(a + ib) – (c + id) = (a – c) + i(b – d)
Multiplication
When two complexes are multiplied by each other, the multiplication process should be similar to the multiplication of two binomials. It means that FOIL method (Distributive multiplication process) is used.
(a + ib). (c + id) = (ac – bd) + i(ad + bc)
Division
The division of two complex number can be performed by multiplying the numerator and denominator by its conjugate value of the denominator, and then applies the FOIL Method.
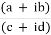 =
=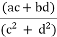 +i
+i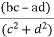
Complex Numbers Identities
Let us see some of the identities:
- (z1 + z2)2 = (z1)2 + (z2)2 + 2 z1 × z2
- (z1 – z2)2 = (z1)2 + (z2)2 – 2 z1 × z2
- (z1)2 – (z2)2 = (z1 + z2)(z1 – z2)
- (z1 + z2)3 = (z1)3 + 3(z1)2 z2 +3(z2)2 z1 + (z2 )3
- (z1 – z2)3 = (z1)3 – 3(z1)2 z2 +3(z2)2 z1 – (z2 )3 a
Properties of Complex Numbers
The properties of complex numbers are listed below:
- The addition of two conjugate complex numbers will result in a real number
- The multiplication of two conjugate complex number will also result in a real number
- If x and y are the real numbers and x+yi =0, then x =0 and y =0
- If p, q, r, and s are the real numbers and p+qi = r+si, then p = r, and q=s
- The complex number obeys the commutative law of addition and multiplication.
z1+z2 = z2+z1
z1. z2 = z2. z1
- The complex number obeys the associative law of addition and multiplication.
(z1+z2) +z3 = z1 + (z2+z3)
(z1.z2).z3 = z1. (z2. z3)
- The complex number obeys the distributive law
z1. (z2+z3) = z1.z2 + z1.z3
- If the sum of two complex number is real, and also the product of two complexnumber is also real, then these complex numbers are conjugate to each other.
- For any two complex numbers, say z1 and z2, then |z1+z2| ≤ |z1|+|z2|
- The result of the multiplication of two complex numbers and its conjugate value should result in a complex number and it should be a positive value.
Modulus and Conjugate:
Let z = a+ib be a complex number.
The Modulus of z is represented by |z|.
Mathematically, |z|=
The conjugate of “z” is denoted by 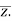
Mathematically,
 = a – ib
= a – ib
ArgandPlane and Polar Representation:
Similar to the XY plane, the Argand(or complex) plane is a system of rectangular coordinates in which the complex number a+ib is represented by the point whose coordinates are a and b.
We find the real and complex components in terms of r and θ, where r is the length of the vector and θ is the angle made with the real axis. Check out the detailed argand plane and polar representation of complex numbers in this article and understand this concept in a detailed way along with solved examples.
Example 1:
Problem: simplify 16 i+10i (3-i)
Solution:
Given,
16i +10i (3-i)
=16i+10i(3i)+10i(-i)
=16i+30i-10i2
=46i-10(-1)
=46i+10
Here real part is 10 and imaginary part is 46
Example 2:
Problem: express the following into a+ib form
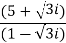
Solution:
Given., 
z = 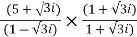 =
= 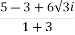 =
= +
+ i
i
Modulus ,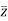 =
=  =
=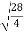 =
= 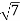
Conjugate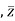 = (
= (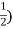 -
- 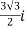
The polar form of complex number is
x+yj where j=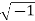
We find the real (horizontal) and imaginary (vertical) components in terms of r (the length of the vector) and θ (the angle made with the real axis):
From Pythagoras, we have
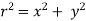
Tan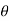 =
= , x= r. Cos
, x= r. Cos y=r.sin
y=r.sin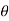
Multiplying the last expression throughout by j gives us
Yj =jr+sin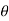
So we can write the polar form of a complex number as
x+yj = r(cos +j sin
+j sin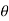 )
)
r is the absolute value of the complex number.
 is the argument of the complex number.
is the argument of the complex number.
There are two other ways of writing the polar form of a complex number:
r cis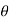 this is just a short hand for r(cos
this is just a short hand for r(cos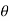 +j sin
+j sin )
)
r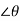 means r(cos
means r(cos +j sin
+j sin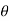 )
)
Example 1:
Find the polar form of 7-5j
Solution:
We need to find r and 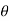
r=
=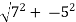
= 
=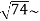 8.6
8.6
To find θ, we first find the acute angle α ,
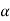 = tan-1(
= tan-1( )
)
= tan-1( )
)
= 35.540
7-5j is in the fourth quadrant so we we have,
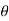 = 3600 -35.540 = 324.460
= 3600 -35.540 = 324.460
So expressing 7-5j in the polar form as.,
7-5j = 8.6(cos324.50 +j sin324.50 )
Example 2:Represent 1+j in polar form
in polar form
 = arctan
= arctan 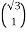 =600
=600
R= 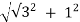 =
= 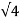 =2
=2
So,
1+j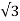 = 2
= 2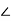 600 = 2( cos600 +jsin 600 )
600 = 2( cos600 +jsin 600 )
De Moiver’s Theorem:
Statement:
For any complex number x and any integer n
r(cos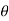 +i sin
+i sin )n = rn (cos(n
)n = rn (cos(n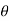 )+isin(n
)+isin(n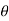 ))
))
Proof:
We will prove this theorem b inaction
We have,
zn=( r(cos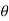 +isin
+isin 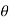 ))n =rn (cos(n
))n =rn (cos(n )+i.sin(n
)+i.sin(n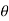 )
)
= rn(cos +i sin
+i sin )n
)n
Now consider,
(cos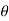 +i sin
+i sin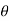 )n for n=1 , we have
)n for n=1 , we have
(cos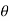 +i sin
+i sin )1 = cos(1.
)1 = cos(1. +isin (1.
+isin (1.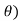
Hence theorem is true for n=1
Now assume that theorem is true for n=k,
Then we have,
(cos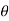 +i sin
+i sin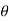 )k= (cos(k
)k= (cos(k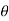 )+i.sin(k
)+i.sin(k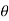 ))
))
For n=k+1 we have,
(cos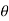 +i sin
+i sin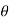 )k+1 =(cos(k+1
)k+1 =(cos(k+1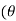 ))+i.sin(k+1
))+i.sin(k+1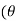 ))
))
We get,
(cos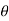 +i sin
+i sin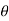 )k+1=(cos
)k+1=(cos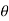 +i sin
+i sin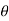 )k (cos
)k (cos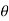 +i sin
+i sin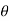 )1
)1
= (cos(k )+isin(k
)+isin(k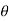 ))(cos(1
))(cos(1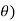 +isin(1
+isin(1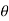 ))
))
= cos (k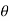 )cos (1
)cos (1 +cos (k
+cos (k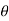 )i sin (1
)i sin (1 ) +i sin(k
) +i sin(k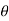 ).cos(1
).cos(1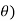 +i2 i sin(k
+i2 i sin(k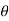 )i sin(1
)i sin(1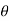 )
)
=cos (k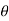 +
+ 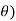 +i sin (k
+i sin (k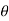 +
+ 
Thus, for n=k+1 we have.,
(cos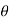 +i sin
+i sin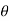 )k+1 =(cos(k+1
)k+1 =(cos(k+1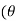 ))+i.sin(k+1
))+i.sin(k+1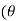 ))
))
Hence the De Moiver’s Theorem is true for all n 1.
1.
Example 1:Write (  ) 7 in the form of a+ib
) 7 in the form of a+ib
First determine the radius ie ., r
Let r= 
r = 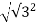 + i2
+ i2
r= 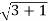
r=2
Now cos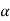 =-
=-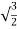 and sin
and sin 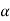 =
= ,
,  must be in the first quadrant and
must be in the first quadrant and 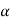 =300
=300
Therefore,
(  ) 7 =
) 7 =  7
7
( 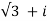 ) 7 = 27 [cos 7.300 +i sin 7.300]
) 7 = 27 [cos 7.300 +i sin 7.300]
= 128[cos 2100+isin2100]
= 128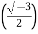 +i
+i 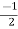
( 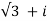 ) 7 = 64
) 7 = 64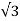 -64 i
-64 i
Example 2:Write ( +i
+i  )4 in the form of a+ib
)4 in the form of a+ib
First we determine the radius,
r = 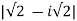
r= 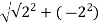
r=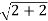
r=2
Now,
( +i
+i 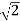 )4 =
)4 =  4
4
= [24 (cos 4.3150 + isin 4.3150)
=16(cos 21600+i sin 21600)
= 16( cos 1800+i.sin 1800)
= 16(-1+0i)
= -16
A function 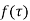 is analytic in a domain if it is analytical at every point of the domain.
is analytic in a domain if it is analytical at every point of the domain.
Position on exponential Trigonometric logarithm
Example; Prove that function 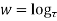 is analytic function.
is analytic function.
Solution. Real and Imaginary parts of 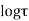 are
are
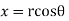
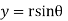
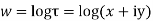
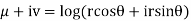
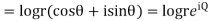
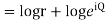
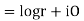
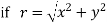

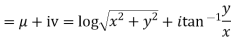
If, 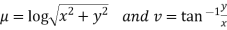
On differentiating u,v we get
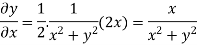
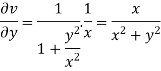
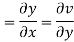
Again differentiating
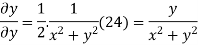
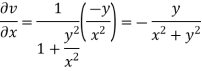

Hence e-R-Equation satisfies.
Properties
(i) Polynomials rational function are entire.
(ii) A differentiable function is always continuous but converse is not true.
Ques Determine P such that the function  analytic
analytic
Ans 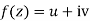
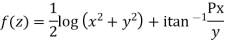
Hence 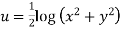
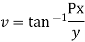
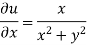
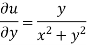


f(z) is analytic Cauchy Riemann should be satisfied that is
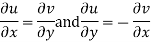
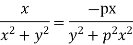
And 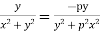
P=-1
Question If  and
and  is an analytic function of z=x+iy find f(z) in terms of z by Milne Thomas method
is an analytic function of z=x+iy find f(z) in terms of z by Milne Thomas method
Answer f(z) is analytic since f is analytic
Let f’=u+iv
Then 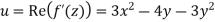

Since u.v satisfy C-R conditions

Integrating w.r.t y we get
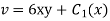
Differentiation v w.r.t x and using second C-R condition we get

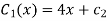
Thus V(x,y)=6xy+4x+
Where  is an arbitrary constant Then
is an arbitrary constant Then 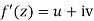

Applying Milne Thomas method replace x by z and y by 0 we get
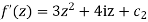
Integrating w.r.t z we get
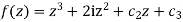
Where 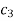 is an arbitrary constant since f(1+ i)=0
is an arbitrary constant since f(1+ i)=0
We get

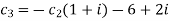
Thus 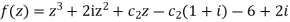
Every polynomial equation having complex coefficients and degree 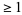 has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial
has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial 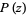 of degree
of degree  has
has  values
values 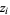 (some of them possibly degenerate) for which
(some of them possibly degenerate) for which  . Such values are called polynomial roots. An example of a polynomial with a single root of multiplicity
. Such values are called polynomial roots. An example of a polynomial with a single root of multiplicity 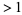 is
is 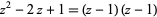 , which has
, which has  as a root of multiplicity 2.
as a root of multiplicity 2.
Example 1:
2y=4x−16 and y=2x−8 perpendicular.
Solution:
Let 2y =4x-16 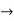 (1)
(1)
Y=2x-8 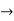 (2)
(2)
Let s write equation (1) in the form of y= mx+c and  2)
2)
 y= 2x-8 and y = 2x-8
y= 2x-8 and y = 2x-8
Here we see that there is only one line,
But if there are two lines , they would have been parallel as the gradients are same.
 y= 2x+5 and y= 2x-8 are parallel
y= 2x+5 and y= 2x-8 are parallel
 y= --
y= -- x-8 and y=2x-8 are perpendicular
x-8 and y=2x-8 are perpendicular
-- are perpendicular.
are perpendicular.
Example 2:
Lisa will make up a punch that is 25% fruit juice by adding pure fruit-juice to a
2-liter mixture that is 10% pure fruit-juice. How many litres of pure fruit juice does she need to add?
Solution:
Let’s call the amount to be found z
Then you will end up with x+2L of 25% juice
This will contain 0.25(x+2) =0.25x+0.5pure juice
The original 2L already contained 0.10.2=0.2 juice
So we added 0.25x=0.3 juice, but this is also x(as x=100% juice).
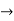 0.25x+0.3=x
0.25x+0.3=x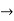 0.75x=0.3
0.75x=0.3  x=0.4 liter
x=0.4 liter
The cardano’s formula:
The Cardano's formula (named after Girolamo Cardano 1501-1576), which is similar to the perfect-square method to quadratic equations, is a standard way to find a real root of a cubic equation l
Ax3+bx3+cx3+d=0.
We can then find the other two roots (real or complex) by polynomial division and the quadratic formula. The solution has two steps. We first "depress" the cubic equation and then solve the depressed equation.
Example :
Finding the real root of the following polynomial equation using cardano’s method
X3+2x2+3x+4=0
Given that ., a=1, b=2, c=3, d=4
Compute Q and R:
Q=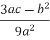 =
= 
R= 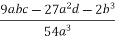 =
=
Compute S and T :
S=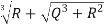 =
= 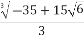
T= 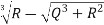 =
= 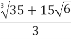
Compute the roots:
X1 = S+T- 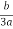
= 
= -1.651
X2 =  -
- +i
+i (s-t)
(s-t)
=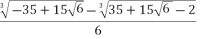 + i.
+ i.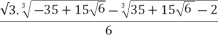
X3 = 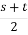 -
-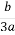 +i
+i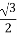 (s-t)
(s-t)
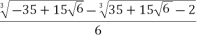 - i.
- i.
 -0.175 -1.547 i.
-0.175 -1.547 i.
The Ferrari method is a method for reducing the solution of an equation of degree 4 over the complex numbers (or, more generally, over any field of characteristic $ne 2,3$) to the solution of one cubic and two quadratics
Given quadratic equation: 36x4 -72x3-391x2-123x+270
Applying Ferrari’s method:
We have,
A=36, B=-72, C=-391, D=-123, E=270

 -
- 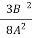 =-
=- 
 -
- 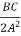 +
+ = -
= -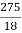
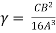 -
- -
-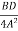 +
+ =
= 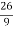
P= - 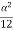 –
–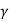 =
=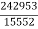 =15.62
=15.62 16
16
Q=  -
- 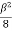 -
-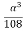 = -
= - 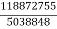 =23.59
=23.59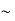 24
24
Finally,
R= -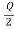
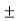
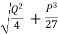 = -
= -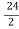
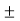

By solving the above equation we get., 12 .
.
Example 2 :
Consider the quadratic equation y4+ay3+by2+cy+d=0
By substituting y= x- the above equation will be reduced to the following
the above equation will be reduced to the following
=X4+ px2+qz+r=0,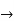 (1)
(1)
The above equation doesn’t contain x3., if one introduces an auxiliary parameter ,then the left hand side of equation (1) can be written as follows:
,then the left hand side of equation (1) can be written as follows:
=X4+ px2+qz+r = (x2 +  +
+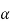 )2 – [2ax2 –qx+(
)2 – [2ax2 –qx+( 2 +p
2 +p +
+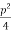 -r)]
-r)] (2)
(2)
= q2 -4.2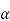 (
( 2 +p
2 +p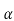 +
+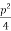 –r) =0
–r) =0
Then the required equation for 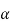 =
= 0 the polynomial in square brackets in equation (2) has one double root
0 the polynomial in square brackets in equation (2) has one double root
X0= 
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson
Unit - 5
Algebra of Complex numbers and Roots of polynomial Equations
Geometric representation of complex numbers
With complex numbers, operations can also be represented geometrically. With the geometric representation of the complex numbers we can recognize new connections, which make it possible to solve further questions.
The complex plane (Gaussian plane)
Complex numbers are defined as numbers in the form z=a+ib or z=a+bi, where i is the imaginary part and a and b are real numbers. A complex number z is thus uniquely determined by the numbers (a,b)(a,b).
The geometric representation of complex numbers is defined as follows
A complex number z=a+ib z=a+ib is assigned the point (a,b)(a,b) in the complex plane. The complex plane is similar to the Cartesian coordinate system, it differs from that in the name of the axes.
The x-axis represents the real part of the complex number. This axis is called real axis and is labelled as Rℝ or Re
The y-axis represents the imaginary part of the complex number. This axis is called imaginary axis and is labelled with iR or Im
The origin of the coordinates is called zero point.
On the complex plane, the number 1 is a unit to the right of the zero point on the real axis and the Number ii is a unit above the zero point on the imaginary axis.
The complex numbers can be represented by points on a two-dimensional Cartesian coordinate system called the complex plane. In this way we establish a one to one correspondence between the set of all complex numbers and the set of all points in the plane. The set of all real numbers corresponds to the real axis x and the set of all purely imaginary numbers corresponds to the imaginary axis y
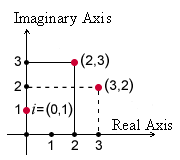
The Cartesian representation of the complex numbers specifies a unique point on the complex plane, and a given point has a unique Cartesian representation of the complex numbers.
Algebraic Operations on Complex Numbers
There can be four types of algebraic operation on complex numbers which are mentioned below. Visit the linked article to know more about these algebraic operations along with solved examples. The four operations on the complex numbers include:
- Addition
- Subtraction
- Multiplication
- Division
Roots of Complex Numbers
When we solve a quadratic equation in the form of ax2 +bx+c = 0, the roots of the equations can be determined in three forms;
- Two Distinct Real Roots
- Similar Root
- No Real roots (Complex Roots)
Complex Number Formulas
While performing the arithmetic operations of complex numbers such as addition and subtraction, combine similar terms. It means that combine the real number with the real number and imaginary number with the imaginary number.
Addition
(a + ib) + (c + id) = (a + c) + i(b + d)
Subtraction
(a + ib) – (c + id) = (a – c) + i(b – d)
Multiplication
When two complexes are multiplied by each other, the multiplication process should be similar to the multiplication of two binomials. It means that FOIL method (Distributive multiplication process) is used.
(a + ib). (c + id) = (ac – bd) + i(ad + bc)
Division
The division of two complex number can be performed by multiplying the numerator and denominator by its conjugate value of the denominator, and then applies the FOIL Method.
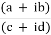 =
=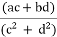 +i
+i
Complex Numbers Identities
Let us see some of the identities:
- (z1 + z2)2 = (z1)2 + (z2)2 + 2 z1 × z2
- (z1 – z2)2 = (z1)2 + (z2)2 – 2 z1 × z2
- (z1)2 – (z2)2 = (z1 + z2)(z1 – z2)
- (z1 + z2)3 = (z1)3 + 3(z1)2 z2 +3(z2)2 z1 + (z2 )3
- (z1 – z2)3 = (z1)3 – 3(z1)2 z2 +3(z2)2 z1 – (z2 )3 a
Properties of Complex Numbers
The properties of complex numbers are listed below:
- The addition of two conjugate complex numbers will result in a real number
- The multiplication of two conjugate complex number will also result in a real number
- If x and y are the real numbers and x+yi =0, then x =0 and y =0
- If p, q, r, and s are the real numbers and p+qi = r+si, then p = r, and q=s
- The complex number obeys the commutative law of addition and multiplication.
z1+z2 = z2+z1
z1. z2 = z2. z1
- The complex number obeys the associative law of addition and multiplication.
(z1+z2) +z3 = z1 + (z2+z3)
(z1.z2).z3 = z1. (z2. z3)
- The complex number obeys the distributive law
z1. (z2+z3) = z1.z2 + z1.z3
- If the sum of two complex number is real, and also the product of two complexnumber is also real, then these complex numbers are conjugate to each other.
- For any two complex numbers, say z1 and z2, then |z1+z2| ≤ |z1|+|z2|
- The result of the multiplication of two complex numbers and its conjugate value should result in a complex number and it should be a positive value.
Modulus and Conjugate:
Let z = a+ib be a complex number.
The Modulus of z is represented by |z|.
Mathematically, |z|=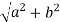
The conjugate of “z” is denoted by 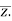
Mathematically,
 = a – ib
= a – ib
ArgandPlane and Polar Representation:
Similar to the XY plane, the Argand(or complex) plane is a system of rectangular coordinates in which the complex number a+ib is represented by the point whose coordinates are a and b.
We find the real and complex components in terms of r and θ, where r is the length of the vector and θ is the angle made with the real axis. Check out the detailed argand plane and polar representation of complex numbers in this article and understand this concept in a detailed way along with solved examples.
Example 1:
Problem: simplify 16 i+10i (3-i)
Solution:
Given,
16i +10i (3-i)
=16i+10i(3i)+10i(-i)
=16i+30i-10i2
=46i-10(-1)
=46i+10
Here real part is 10 and imaginary part is 46
Example 2:
Problem: express the following into a+ib form

Solution:
Given., 
z =  =
=  =
= +
+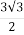 i
i
Modulus ,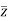 =
= 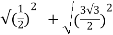 =
=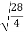 =
= 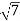
Conjugate = (
= (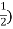 -
- 
The polar form of complex number is
x+yj where j=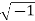
We find the real (horizontal) and imaginary (vertical) components in terms of r (the length of the vector) and θ (the angle made with the real axis):
From Pythagoras, we have
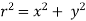
Tan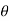 =
= , x= r. Cos
, x= r. Cos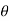 y=r.sin
y=r.sin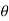
Multiplying the last expression throughout by j gives us
Yj =jr+sin
So we can write the polar form of a complex number as
x+yj = r(cos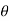 +j sin
+j sin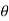 )
)
r is the absolute value of the complex number.
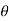 is the argument of the complex number.
is the argument of the complex number.
There are two other ways of writing the polar form of a complex number:
r cis this is just a short hand for r(cos
this is just a short hand for r(cos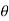 +j sin
+j sin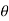 )
)
r means r(cos
means r(cos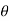 +j sin
+j sin )
)
Example 1:
Find the polar form of 7-5j
Solution:
We need to find r and 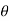
r=
=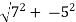
= 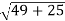
=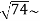 8.6
8.6
To find θ, we first find the acute angle α ,
 = tan-1(
= tan-1( )
)
= tan-1( )
)
= 35.540
7-5j is in the fourth quadrant so we we have,
 = 3600 -35.540 = 324.460
= 3600 -35.540 = 324.460
So expressing 7-5j in the polar form as.,
7-5j = 8.6(cos324.50 +j sin324.50 )
Example 2:Represent 1+j in polar form
in polar form
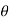 = arctan
= arctan 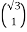 =600
=600
R= 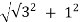 =
=  =2
=2
So,
1+j = 2
= 2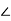 600 = 2( cos600 +jsin 600 )
600 = 2( cos600 +jsin 600 )
De Moiver’s Theorem:
Statement:
For any complex number x and any integer n
r(cos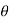 +i sin
+i sin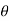 )n = rn (cos(n
)n = rn (cos(n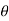 )+isin(n
)+isin(n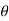 ))
))
Proof:
We will prove this theorem b inaction
We have,
zn=( r(cos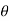 +isin
+isin  ))n =rn (cos(n
))n =rn (cos(n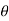 )+i.sin(n
)+i.sin(n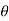 )
)
= rn(cos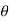 +i sin
+i sin )n
)n
Now consider,
(cos +i sin
+i sin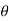 )n for n=1 , we have
)n for n=1 , we have
(cos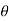 +i sin
+i sin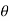 )1 = cos(1.
)1 = cos(1.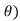 +isin (1.
+isin (1.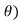
Hence theorem is true for n=1
Now assume that theorem is true for n=k,
Then we have,
(cos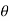 +i sin
+i sin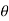 )k= (cos(k
)k= (cos(k )+i.sin(k
)+i.sin(k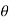 ))
))
For n=k+1 we have,
(cos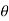 +i sin
+i sin )k+1 =(cos(k+1
)k+1 =(cos(k+1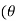 ))+i.sin(k+1
))+i.sin(k+1 ))
))
We get,
(cos +i sin
+i sin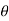 )k+1=(cos
)k+1=(cos +i sin
+i sin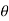 )k (cos
)k (cos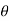 +i sin
+i sin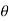 )1
)1
= (cos(k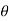 )+isin(k
)+isin(k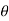 ))(cos(1
))(cos(1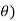 +isin(1
+isin(1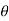 ))
))
= cos (k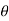 )cos (1
)cos (1 +cos (k
+cos (k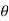 )i sin (1
)i sin (1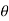 ) +i sin(k
) +i sin(k ).cos(1
).cos(1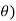 +i2 i sin(k
+i2 i sin(k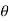 )i sin(1
)i sin(1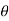 )
)
=cos (k +
+  +i sin (k
+i sin (k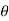 +
+ 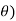
Thus, for n=k+1 we have.,
(cos +i sin
+i sin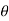 )k+1 =(cos(k+1
)k+1 =(cos(k+1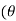 ))+i.sin(k+1
))+i.sin(k+1 ))
))
Hence the De Moiver’s Theorem is true for all n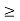 1.
1.
Example 1:Write ( 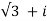 ) 7 in the form of a+ib
) 7 in the form of a+ib
First determine the radius ie ., r
Let r= 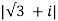
r = 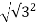 + i2
+ i2
r= 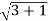
r=2
Now cos =-
=-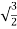 and sin
and sin 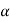 =
= ,
, 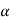 must be in the first quadrant and
must be in the first quadrant and 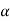 =300
=300
Therefore,
( 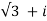 ) 7 =
) 7 = 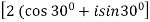 7
7
( 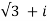 ) 7 = 27 [cos 7.300 +i sin 7.300]
) 7 = 27 [cos 7.300 +i sin 7.300]
= 128[cos 2100+isin2100]
= 128 +i
+i 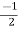
(  ) 7 = 64
) 7 = 64 -64 i
-64 i
Example 2:Write (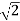 +i
+i  )4 in the form of a+ib
)4 in the form of a+ib
First we determine the radius,
r = 
r= 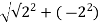
r=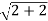
r=2
Now,
( +i
+i 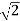 )4 =
)4 =  4
4
= [24 (cos 4.3150 + isin 4.3150)
=16(cos 21600+i sin 21600)
= 16( cos 1800+i.sin 1800)
= 16(-1+0i)
= -16
A function 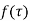 is analytic in a domain if it is analytical at every point of the domain.
is analytic in a domain if it is analytical at every point of the domain.
Position on exponential Trigonometric logarithm
Example; Prove that function 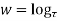 is analytic function.
is analytic function.
Solution. Real and Imaginary parts of 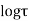 are
are
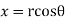

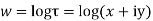
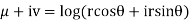
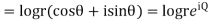
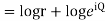
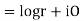



If, 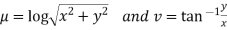
On differentiating u,v we get
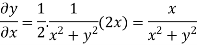


Again differentiating

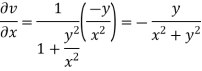

Hence e-R-Equation satisfies.
Properties
(i) Polynomials rational function are entire.
(ii) A differentiable function is always continuous but converse is not true.
Ques Determine P such that the function  analytic
analytic
Ans 
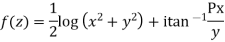
Hence 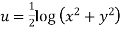
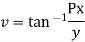
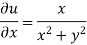
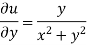
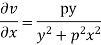

f(z) is analytic Cauchy Riemann should be satisfied that is
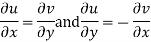

And 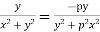
P=-1
Question If  and
and  is an analytic function of z=x+iy find f(z) in terms of z by Milne Thomas method
is an analytic function of z=x+iy find f(z) in terms of z by Milne Thomas method
Answer f(z) is analytic since f is analytic
Let f’=u+iv
Then 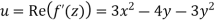

Since u.v satisfy C-R conditions
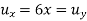
Integrating w.r.t y we get
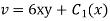
Differentiation v w.r.t x and using second C-R condition we get
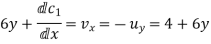
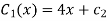
Thus V(x,y)=6xy+4x+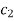
Where 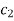 is an arbitrary constant Then
is an arbitrary constant Then 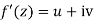
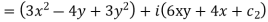
Applying Milne Thomas method replace x by z and y by 0 we get
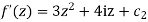
Integrating w.r.t z we get
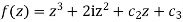
Where 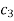 is an arbitrary constant since f(1+ i)=0
is an arbitrary constant since f(1+ i)=0
We get
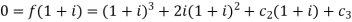
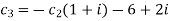
Thus 
Every polynomial equation having complex coefficients and degree  has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial
has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial 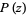 of degree
of degree  has
has  values
values  (some of them possibly degenerate) for which
(some of them possibly degenerate) for which 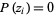 . Such values are called polynomial roots. An example of a polynomial with a single root of multiplicity
. Such values are called polynomial roots. An example of a polynomial with a single root of multiplicity 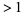 is
is 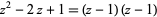 , which has
, which has  as a root of multiplicity 2.
as a root of multiplicity 2.
Example 1:
2y=4x−16 and y=2x−8 perpendicular.
Solution:
Let 2y =4x-16  (1)
(1)
Y=2x-8  (2)
(2)
Let s write equation (1) in the form of y= mx+c and 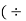 2)
2)
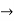 y= 2x-8 and y = 2x-8
y= 2x-8 and y = 2x-8
Here we see that there is only one line,
But if there are two lines , they would have been parallel as the gradients are same.
 y= 2x+5 and y= 2x-8 are parallel
y= 2x+5 and y= 2x-8 are parallel
 y= --
y= -- x-8 and y=2x-8 are perpendicular
x-8 and y=2x-8 are perpendicular
-- are perpendicular.
are perpendicular.
Example 2:
Lisa will make up a punch that is 25% fruit juice by adding pure fruit-juice to a
2-liter mixture that is 10% pure fruit-juice. How many litres of pure fruit juice does she need to add?
Solution:
Let’s call the amount to be found z
Then you will end up with x+2L of 25% juice
This will contain 0.25(x+2) =0.25x+0.5pure juice
The original 2L already contained 0.10.2=0.2 juice
So we added 0.25x=0.3 juice, but this is also x(as x=100% juice).
 0.25x+0.3=x
0.25x+0.3=x 0.75x=0.3
0.75x=0.3  x=0.4 liter
x=0.4 liter
The cardano’s formula:
The Cardano's formula (named after Girolamo Cardano 1501-1576), which is similar to the perfect-square method to quadratic equations, is a standard way to find a real root of a cubic equation l
Ax3+bx3+cx3+d=0.
We can then find the other two roots (real or complex) by polynomial division and the quadratic formula. The solution has two steps. We first "depress" the cubic equation and then solve the depressed equation.
Example :
Finding the real root of the following polynomial equation using cardano’s method
X3+2x2+3x+4=0
Given that ., a=1, b=2, c=3, d=4
Compute Q and R:
Q=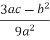 =
= 
R=  =
=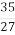
Compute S and T :
S= =
= 
T= 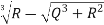 =
= 
Compute the roots:
X1 = S+T- 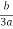
= 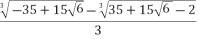
= -1.651
X2 =  -
-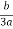 +i
+i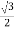 (s-t)
(s-t)
=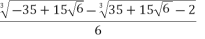 + i.
+ i.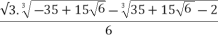
X3 =  -
-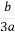 +i
+i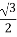 (s-t)
(s-t)
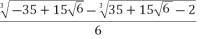 - i.
- i.
 -0.175 -1.547 i.
-0.175 -1.547 i.
The Ferrari method is a method for reducing the solution of an equation of degree 4 over the complex numbers (or, more generally, over any field of characteristic $ne 2,3$) to the solution of one cubic and two quadratics
Given quadratic equation: 36x4 -72x3-391x2-123x+270
Applying Ferrari’s method:
We have,
A=36, B=-72, C=-391, D=-123, E=270

 -
- 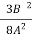 =-
=- 
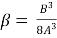 -
- 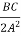 +
+ = -
= -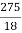
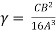 -
-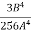 -
-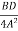 +
+ =
= 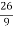
P= - 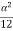 –
– =
= =15.62
=15.62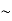 16
16
Q=  -
- 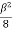 -
- = -
= - 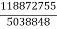 =23.59
=23.59 24
24
Finally,
R= -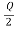
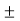
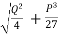 = -
= -
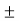
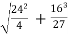
By solving the above equation we get., 12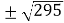 .
.
Example 2 :
Consider the quadratic equation y4+ay3+by2+cy+d=0
By substituting y= x- the above equation will be reduced to the following
the above equation will be reduced to the following
=X4+ px2+qz+r=0,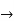 (1)
(1)
The above equation doesn’t contain x3., if one introduces an auxiliary parameter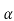 ,then the left hand side of equation (1) can be written as follows:
,then the left hand side of equation (1) can be written as follows:
=X4+ px2+qz+r = (x2 + 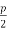 +
+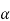 )2 – [2ax2 –qx+(
)2 – [2ax2 –qx+( 2 +p
2 +p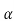 +
+ -r)]
-r)] (2)
(2)
= q2 -4.2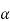 (
(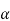 2 +p
2 +p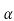 +
+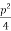 –r) =0
–r) =0
Then the required equation for 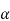 =
=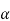 0 the polynomial in square brackets in equation (2) has one double root
0 the polynomial in square brackets in equation (2) has one double root
X0= 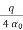
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson