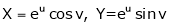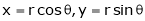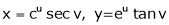Unit - 3
Applications of Partial differentiation
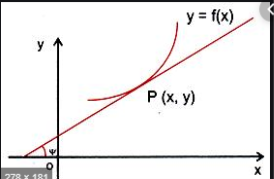
The tangent is a line which passes through a single point of the curve. Also known as slope of the curve.
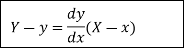 Let
Let 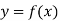 be the curve in the XY plane. Then the equation of the tangent at a point P(x,y) in the XY plane is given by
be the curve in the XY plane. Then the equation of the tangent at a point P(x,y) in the XY plane is given by
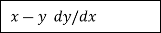 Intercepts: The equation of the intercept that meet the x axis is (Y=0)
Intercepts: The equation of the intercept that meet the x axis is (Y=0)
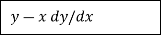 And the equation of the intercept that meet the y axis is (X=0).
And the equation of the intercept that meet the y axis is (X=0).
Example1: Find the equation of the tangent to the curve 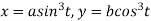 at the point
at the point 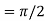 ?
?
Given Curve 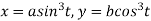
Differentiating both side with respect to t.
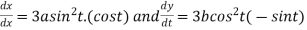
By Chain Rule 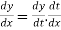
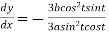
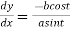
Therefore the equation of the tangent
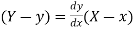
Or 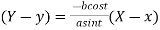 …(i)
…(i)
At the point 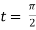
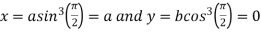
Also 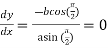
Substituting all these values in (i) we get
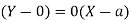
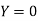
Hence the equation of the tangent is 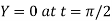 .
.
Example2: At what point is the tangent to the curve 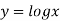 parallel to the chord joining the points (0,0) and (0,1).
parallel to the chord joining the points (0,0) and (0,1).
Given curve is 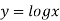
Equation of the chord joining the points (0,0) and (0,1) is

Or 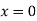 i.e. Parallel toY-axis …(i)
i.e. Parallel toY-axis …(i)
Given curve is 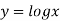
Differentiating both side with respect to x.
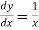
Equation of tangent parallel to Y-axis is 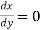
Or  (as above)
(as above)
Since curve is 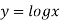
At 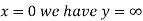 (ii)
(ii)
From (i) and (ii) we conclude that the point tangent parallel to the chord is 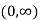 .
.
Hence the point tangent parallel to the chord is 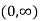 .
.
Example3: Prove that 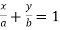 touches the curve
touches the curve 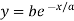 at the point where the curve crosses the axis of y.
at the point where the curve crosses the axis of y.
Given curve is 
It will cross the y-axis at x=0, we get
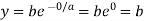
Hence the point of the curve on the Y-axis is 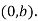
Since curve is 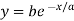
Differentiating both side with respect to x, we get
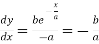
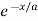 .
.
At point (0,b) we have 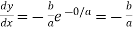 …(i)
…(i)
Again given 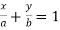
Differentiating both side with respect to x, we get
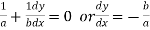
Again at the point (0,b) we have 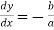 …..(ii)
…..(ii)
As we know that two curve touches each other then they have Same Lope at the point of intersection.
From (i) and (ii) we conclude that both the curve touches each other on Y-axis.
Normal:
A normal is a line which passes through a point and is perpendicular to the normal at there.
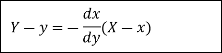 Let
Let 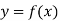 be the curve in the XY plane. Then the equation of the normal at a point P(x,y) in the XY plane is given by
be the curve in the XY plane. Then the equation of the normal at a point P(x,y) in the XY plane is given by
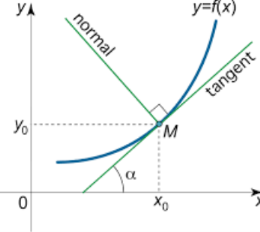
Angle of intersection of two curves:
Angle of intersection of two curves is formed at the intersection point of tangents to the curve.
Procedure: 1. Solve the given equations of the curve to get the point of intersection let it be M.
2. Find out the slopes of the given curves (i.e. 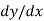 ) at point M. Let the slope of first curve be
) at point M. Let the slope of first curve be 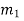 and second be
and second be 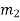 .
.
3. Let the angle at the point M be 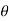 . Then
. Then
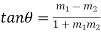
In case 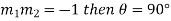 it means the curves are orthogonal to each other.
it means the curves are orthogonal to each other.
Lengths of Tangent and Normal
The length of the following is given by formulas:
- Tangent =

- Normal =
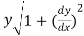
- Sub tangent =
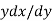
- Sub normal=
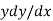 .
.
Example1: Find the equation of the normal of the curve  at
at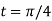 .
.
Given curve 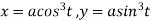
Differentiating both side with respect to t.
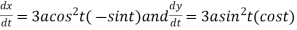
By Chain Rule 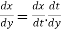
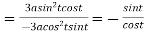
At the point 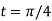 ,
,

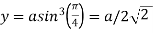
Also 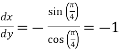
Therefore equation of the normal at 
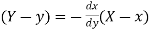
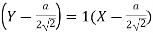
Hence the equation of the normal at 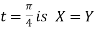 .
.
Example2: Prove that the curve  and
and 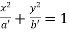 will cut orthogonally if
will cut orthogonally if 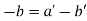 ?
?
Given curves 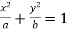 …(i)
…(i)
And 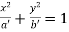 …(ii)
…(ii)
Let 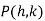 be a intersection point of curve (i) and (ii)
be a intersection point of curve (i) and (ii)
Then 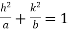
And 
On solving we get
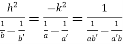
Or 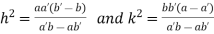 …(iii)
…(iii)
Differentiating (i) with respect to x.
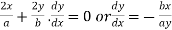
At the point 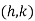 slope of (i) is given by
slope of (i) is given by 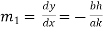
Differentiating (ii) with respect to x.
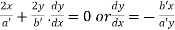
At the point 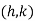 slope of (ii) is given by
slope of (ii) is given by 
For orthogonal intersection, we have 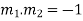
Substituting the values of slopes we get,
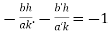
Or 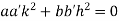
Putting values from (iii) we get
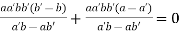

Or 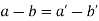
Hence proved.
Example3: Find the lengths of the tangent, normal, sub tangent and subnormal for the cycloid:
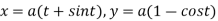
The equation of the cycloid 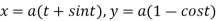
Differentiating both with respect to t .

By Chain Rule
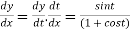
Length of tangent is 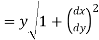
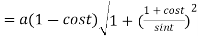

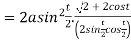
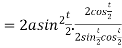

Length of normal is 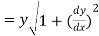

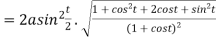
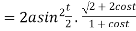
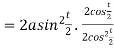
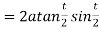
Length of sub tangent =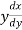
=
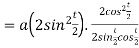
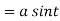
Length of sub normal =
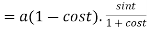
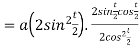

Let 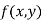 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 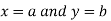 is said to be a maximum point of
is said to be a maximum point of 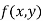 if
if
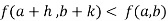
Or 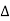 =
= 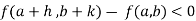
For all positive and negative values of h and k.
Similarly the point 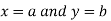 is said to be a minimum point of
is said to be a minimum point of 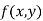 if
if
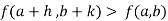
Or  =
= 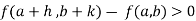
For all positive and negative values of h and k.
Saddle point: Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643290640_7940006.png)
At the point.
Stationary Value
The value  is said to be a stationary value of
is said to be a stationary value of 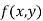 if
if
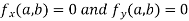
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 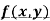
- Calculate
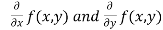 .
. - Form and solve
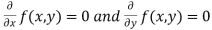 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 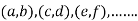
- Calculate the following values :

4. (a) If 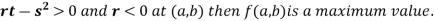
(b) If 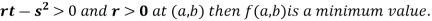
(c) If 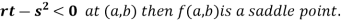
(d) If 
Example1 Find out the maxima and minima of the function
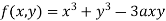
Given 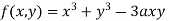 …(i)
…(i)
Partially differentiating (i) with respect to x we get
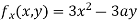 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
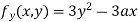 ….(iii)
….(iii)
Now, form the equations 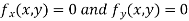
Using (ii) and (iii) we get
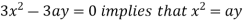
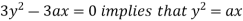
 using above two equations
using above two equations
Squaring both side we get
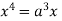
Or 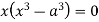
This show that 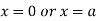
Also we get 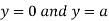
Thus we get the pair of value as 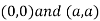
Now, we calculate
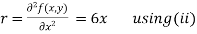
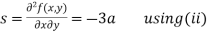

Putting above values in
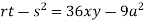
At point (0,0) we get

So, the point (0,0) is a saddle point.
At point 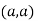 we get
we get
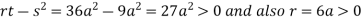
So the point 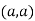 is the minimum point where
is the minimum point where 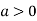
In case 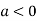
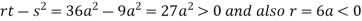
So the point 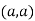 is the maximum point where
is the maximum point where 
Example2 Find the maximum and minimum point of the function
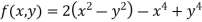
Partially differentiating given equation with respect to and x and y then equate them to zero
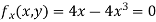
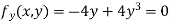
On solving above we get 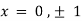
Also 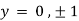
Thus, we get the pair of values (0,0), (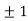 ,0) and (0,
,0) and (0,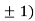
Now, we calculate

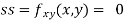
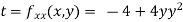
At the point (0,0)
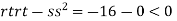
So function has saddle point at (0,0).
At the point (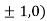
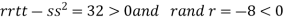
So the function has maxima at this point (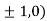 .
.
At the point (0,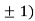

So the function has minima at this point (0,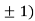 .
.
At the point (
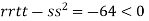
So the function has an saddle point at (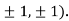
Generally to calculate the stationary value of a function with some relation by converting the given function into the least possible independent variables and then solve them. When this method fail, we use Lagrange’s method.
This method is used to calculate the stationary value of a function of several variables which are all not independent but are connected by some relation.
Let 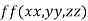 be the function in the variable x, y and z which is connected by the relation
be the function in the variable x, y and z which is connected by the relation 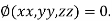
Rule: a) Form the equation
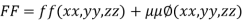
Where 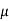 is a parameter.
is a parameter.
b) Form the equation using partial differentiation is
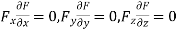
(We always try to eliminate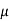 )
)
c) Solve the all above equation with the given relation 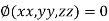
These give the value of 
These value obtained when substituted in the given function will give the stationary value of the function.
Example1 Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f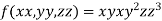
And the relation 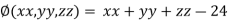
By Lagrange’s Method

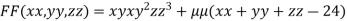 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
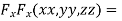
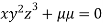 ….(ii)
….(ii)
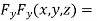
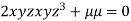 ….(iii)
….(iii)
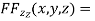
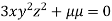 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
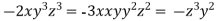
On solving
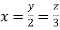
Putting it in given relation we get
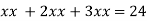
Or 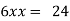
Or 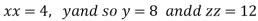
Thus the first number is 4 second is 8 and third is 12
Example2 The temperature T at any point 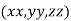 in space is
in space is  .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Given function is 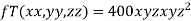
On the surface of unit sphere given 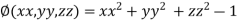 [
[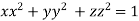 is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
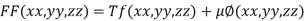
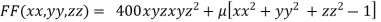 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
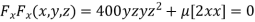 or
or 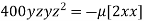 …(ii)
…(ii)
 or
or 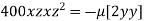 …(iii)
…(iii)
 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get
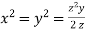
Using given relation 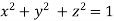
Or 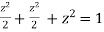
Or 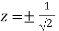
So that 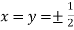
Or 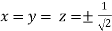
Thus points are 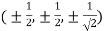
The maximum temperature is 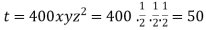
Example3 If 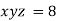 ,Find the value of x and y for which
,Find the value of x and y for which 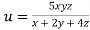 is maximum.
is maximum.
Given function is 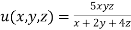
And relation is 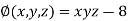
By Lagrange’s Method
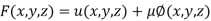
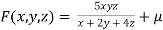 [
[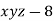 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
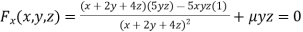
Or  …(ii)
…(ii)
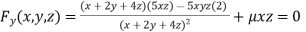
Or 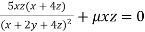 …(iii)
…(iii)
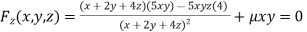
Or 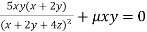 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
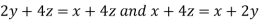
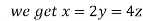
Using the given relation we get 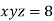
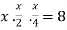
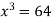

So that 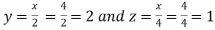
Thus the point for the maximum value of the given function is 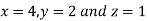
Example4: Find the points on the surface 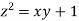 nearest to the origin.
nearest to the origin.
Let  be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin 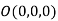 is
is
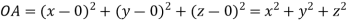
Thus the given equation will be
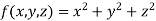
And relation is 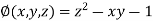
By Lagrange’s Method
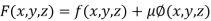
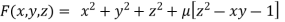 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
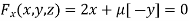
Or 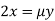 …(ii)
…(ii)
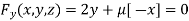
Or 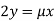 …(iii)
…(iii)
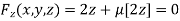
Or 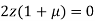
Or 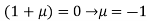
On solving equation (ii) by (iii) we get
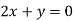
And 
On subtracting we get 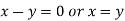
Putting in above 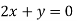
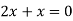
Or 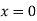
Thus 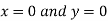
Using the given relation we get
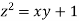 = 0.0 +1=1
= 0.0 +1=1
Or 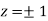
Thus point on the surface nearest to the origin is 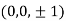
Jacobians, Errors and Approximations, maxima and minima
Jacobians
If u and v be continuous and differentiable functions of two other independent variables x and y such as
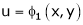 ,
,  then we define the determine
then we define the determine
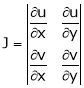 as Jacobian of u, v with respect to x, y
as Jacobian of u, v with respect to x, y
Similarly ,
JJ’ = 1
Actually Jacobins are functional determines
Ex.
 Calculate
Calculate 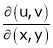
- If
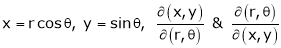
- If
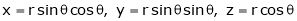
ST 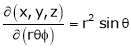
4.  find
find 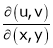
5. If 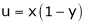 and
and 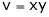 , find
, find 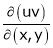
6. 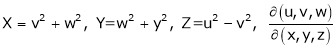
7. If 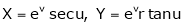
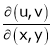
8. If 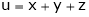 ,
, 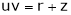 ,
, 
JJ1 = 1
If  ,
, 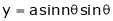
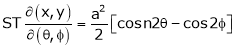
JJ1=1
Jacobian of composite function (chain rule)
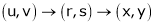
Then 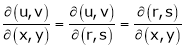
Ex.
- If
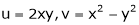
Where 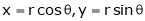

2. If 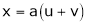
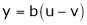 and
and 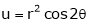

Find 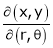
3. If 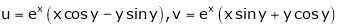
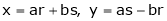
Find 
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
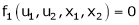 ,
, 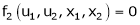
Then 
Similarly,
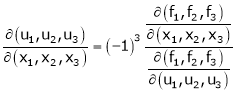
Ex.
If 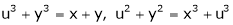
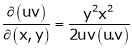
If 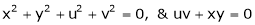
Find 
Partial derivative of implicit functions
Consider four variables u, v, x, y related by implicit function.
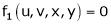 ,
, 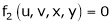
Then
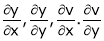

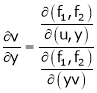
Ex.
If 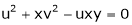 and
and 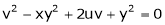
Find 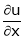
If 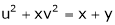 and
and 
Find 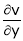
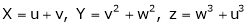
Find 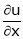
If 
Find 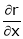
The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because:
* The measurement of the data is not precise due to the instruments. (e.g., the accurate reading of a piece of paper is 4.5 cm but since the ruler does not use decimals, you round it to 5 cm.) or
* Approximations are used instead of the real data (e.g., 3.14 instead of π).
In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm.
One commonly distinguishes between the relative error and the absolute error.
Given some value v and its approximation v approx, the absolute error is
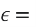 |
|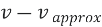 |
|
where the vertical bars denote the absolute value. If v ≠0 , the relative error is
 =
= =|
=| 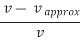 | = | 1 -
| = | 1 - 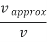 |
|
And the percent error is.,
 =100%.
=100%.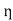 = 100 %.
= 100 %. =100%.| 1 -
=100%.| 1 - 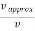 |
|
In words, the absolute error is the magnitude of the difference between the exact value and the approximation. The relative error is the absolute error divided by the magnitude of the exact value. The percent error is the relative error expressed in terms of per 100.
An error bound is an upper limit on the relative or absolute size of an approximation error.
Example 1:
If the exact value is 50 and the approximation is 49.9, then the absolute error is 0.1 and the relative error is 0.1/50 = 0.002 = 0.2%.
Example 2:
If in measuring a 6 mL beaker, the value read was 5 mL. The correct reading being 6 mL, this means the percent error in that particular situation is, rounded, 16.7%.
Example 3:
Compute the error and relative error when xT=0.3320 and xA=0.3321.
Using the formula above, we have that the error of xA from xT is:
(1)
Error (xA)=xT−xA=0.3320−0.3321=−0.0001
Now the relative error of xA from xT is:
(2)
Rel(xA)=xT−xAxT=−0.00010.3320≈−0.00030120
Example 4:
A polynomial p(x) is used to approximate a function f(x) that is difficult to compute at x=0. We find that p(0)=9.1111334 and the true value f(0)=9.1122114. Find the error and relative error of p(0) from f(0).
Using the formula above, we have that the error of p(0) (our approximate value) from f(0) (the actual value) is:
(3)
Error(p(0))=f(0)−p(0)=9.1122114−9.1111334=0.001078
Now the relative error of p(0) from f(0) is:
(4)
Rel(p0)=f(0)−p(0)f(0)=0.0010789.1122114≈0.0001183...
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson