Unit - 2
Partial differentiation
Partial Differentiation of composite function
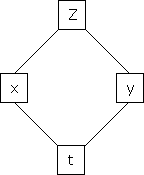
a) Let 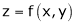 and
and 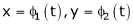 , then z becomes a function of
, then z becomes a function of 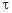 , In this case z is called composite function of
, In this case z is called composite function of 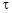 .
.
i.e.
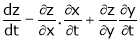
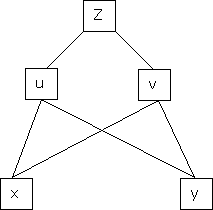
b) Let 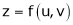 possess continuous partial derivatives and let
possess continuous partial derivatives and let 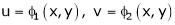 possess continuous partial derivatives, then z is called composite function of x and y.
possess continuous partial derivatives, then z is called composite function of x and y.
i.e.

&
Continuing in this way, …..
Ex. If 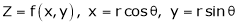 Then prove that
Then prove that
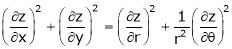
Ex. If 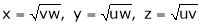 then prove that
then prove that
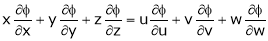
Where  is function of x, y, z.
is function of x, y, z.
Ex. If 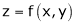 where
where 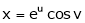 ,
,
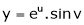 then show that,
then show that,
i) 
Ii) 
Notations of partial derivatives of variable to be treated as a constant
Let
 and
and 
i.e.

Then 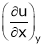 means partial derivative of u w.r.t. x treating y const.
means partial derivative of u w.r.t. x treating y const.
To find  from given reactions we first express x in terms of u & v.
from given reactions we first express x in terms of u & v.
i.e. 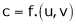 & then diff. x w.r.t. u treating v constant.
& then diff. x w.r.t. u treating v constant.
To find 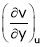 express v as a function of y and u i.e.
express v as a function of y and u i.e. 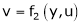 then diff. v w.r.t. y treating u as a const.
then diff. v w.r.t. y treating u as a const.
Ex. If  ,
, 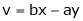 then find the value of
then find the value of
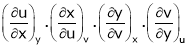 .
.
Ex. If  ,
, 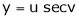 then prove that
then prove that
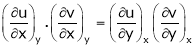
A polynomial in x & y is said to be Homogeneous expression in x & y of degree n. If the degree of each term in the expression is same & equal to n.
e.g.
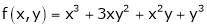 is a homogeneous function of degree 3.
is a homogeneous function of degree 3.
To find the degree of homogeneous expression f(x, y).
- Consider
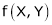
- Put
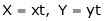 . Then if we get
. Then if we get  .
.
Then the degree of 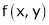 is n.
is n.
Ex.
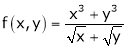
Consider 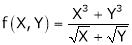
Put 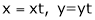
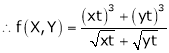

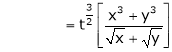
 .
.
Thus degree of f(x, y) is 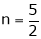
Note that
If 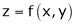 be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
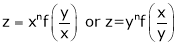
Differentiation of Implicit function
Suppose that we cannot find y explicitly as a function of x. But only implicitly through the relation f(x, y) = 0.
Then we find 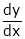
Since 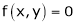
 diff. P. w.r.t. x we get
diff. P. w.r.t. x we get
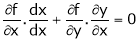
i.e. 
Similarly,
It f (x, y, z) = 0 then z is called implicit function of x, y. Then in this case we get
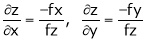
Ex.
Find 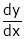 if
if 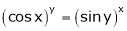
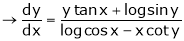
Ex. Find  . If
. If 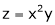 , &
, &
Ex. If 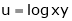 , where
, where 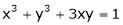
Find 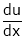
Ex. If 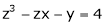
Then find 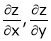
Eulers Theorem on Homogeneous functions:
Statement:
If 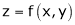 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
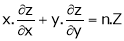
Deductions from Eulers theorem
- If
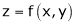 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
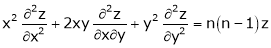 .
.
2. If 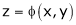 be a homogeneous functions of degree n in x & y and also
be a homogeneous functions of degree n in x & y and also 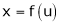 then,
then,
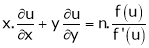
And
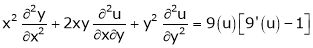
Where 
Ex.
If 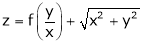 , find the value of
, find the value of

Ex.
If 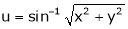 then find the value of
then find the value of 
Ex. If 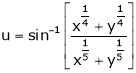 then prove
then prove
That 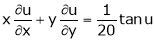
Ex. If  the prove that
the prove that
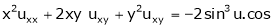
Ex. If then show
then show
That 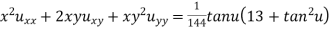
In calculus, the general Leibniz rulenamed after Gottfried Wilhelm Leibniz, generalizes the product rule (which is also known as "Leibniz's rule"). It states that if f and g are n-times differentiable functions, then the product fg is also n-times differentiable and its nth derivative is given by
(fg)n = 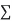 k=0n (nk) f(n-k).g(k)
k=0n (nk) f(n-k).g(k)
Alternatively, by letting F = f ∘ g (equiv., F(x) = f(g(x)) for all x), one can also write the chain rule in Lagrange's notation, as follows:
F’(X)= f’(g(x)).g’(x)
The chain rule may also be rewritten in Leibniz's notation in the following way. If a variable z depends on the variable y, which itself depends on the variable x (i.e., y and z are dependent variables), then z, via the intermediate variable of y, depends on x as well. In which case, the chain rule states that:

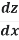 =
= 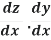
The Chain Rule Formula is as follows –
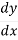 =
= .
.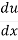
Solved Examples
Example 1: Differentiate y = cos x2
Solution:
Given,
y = cos x2
Let u = x2, so that y = cos u
Therefore: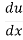 =2x
=2x
 = -sin u
= -sin u
And so, the chain rule says:
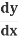 =
=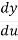 .
.
 = -sin u × 2x
= -sin u × 2x
= -2x sin x2
Example 2:
Differentiate f(x)=(1+x2)5.
Solution:
Using the Chain rule,
 =
= 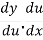
Let us take y = u5 and u = 1+x2
Then 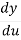 =
= 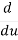 (u5) = 5u4
(u5) = 5u4
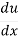 =
= 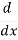 (1 + x2 )= 2x.
(1 + x2 )= 2x.
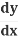 = 5u4⋅2x = 5(1+x2)4⋅2x
= 5u4⋅2x = 5(1+x2)4⋅2x
= 10x(1+x4)
3. Implicit differentiation
Implicit differentiation:
A function can be explicit or implicit:
Explicit: "y = some function of x". When we know x we can calculate y directly.
Implicit: "some function of y and x equals something else". Knowing x does not lead directly to y.
How to do Implicit Differentiation
- Differentiate with respect to x
- Collect all the
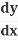 on one side
on one side - Solve for
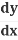
Example 1: x2 + y2 = r2
Differentiate with respect to x:
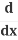 (x2) +
(x2) +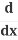 (y2) =
(y2) = (r2)
(r2)
Let's solve each term:
Use the Power Rule: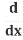 (x2) = 2x
(x2) = 2x
Use the Chain Rule (explained below):  (y2) = 2y
(y2) = 2y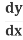
r2 is a constant, so its derivative is 0:d/dx(r2) = 0
Which gives us:
2x + 2y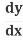 = 0
= 0
Collect all the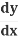 on one side
on one side
Y 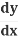 = −x
= −x
Solve for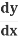 :
:
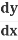 =-
=- 
The Chain Rule Using  :
:
Let's look more closely at how 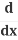 (y2) becomes 2y
(y2) becomes 2y 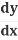
The Chain Rule says:
 =
=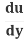 .
.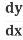
Substitute in u = y2:
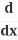 (y2) =
(y2) =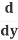 (y2) .
(y2) .
And then:
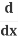 (y2) = 2y
(y2) = 2y
Basically, all we did was differentiate with respect to y and multiply by dy/dx
Example 2:
The following problems require the use of implicit differentiation. Implicit differentiation is nothing more than a special case of the well-known chain rule for derivatives. The majority of differentiation problems in first-year calculus involve functions y written EXPLICITLY as functions of x. For example, if
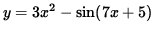 ,
,
Then the derivative of y is
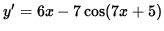 .
.
However, some functions y is written IMPLICITLY as functions of x. A familiar example of this is the equation
x2 + y2 = 25,
Which represents a circle of radius five cantered at the origin. Suppose that we wish to find the slope of the line tangent to the graph of this equation at the point (3, -4) .
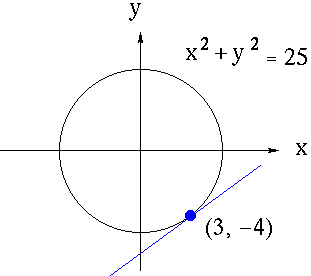
How could we find the derivative of y in this instance? One way is to first write y explicitly as a function of x. Thus,
x2 + y2 = 25,
y2 = 25 - x2,
And
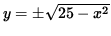 ,
,
Where the positive square root represents the top semi-circle and the negative square root represents the bottom semi-circle. Since the point
(3, -4) lies on the bottom semi-circle given by
 ,
,
The derivative of y is
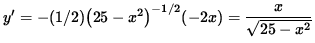 ,
,
i.e.,
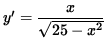 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
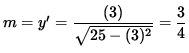 .
.
Unfortunately, not every equation involving x and y can be solved explicitly for y . For the sake of illustration we will find the derivative of y WITHOUT writing y explicitly as a function of x . Recall that the derivative (D) of a function of x squared, (f(x))2 , can be found using the chain rule :
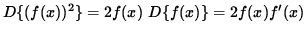 .
.
Since y symbolically represents a function of x, the derivative of y2 can be found in the same fashion :
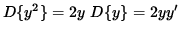 .
.
Now begin with
x2 + y2 = 25 .
Differentiate both sides of the equation, getting
D ( x2 + y2 ) = D ( 25 ) ,
D ( x2 ) + D ( y2 ) = D ( 25 ) ,
And
2x + 2 y y' = 0 ,
So that
2 y y' = - 2x ,
And
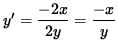 ,
,
i.e.,
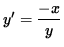 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
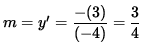 .
.
The total differential is:
Dz=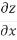 dx+
dx+ 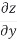 dy
dy
EXAMPLE 1:
Find the total differential of w=x3yz + xy +z +3 at (1,2,3)
Sol: the total differential at the point ( x0,y0,z0) is
Dw= wx( x0,y0,z0).dx +wy( x0,y0,z0).dy+wz( x0,y0,z0).dz
In our case,
wx=3x2yz+y wy=x3z+x wz=x3y+1
Substituting in the point (1,2,3) we get
wx(1,2,3)=20
wy(1,2,3)=4
wz(1,2,3)=3
Thus, the total differential is.,
Dw= 20dx+4dy+3dz.
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson