Unit - 1
Higher order derivatives and applications
SET THEORY:
The theory had the revolutionary aspect of treating infinite sets as mathematical objects that are on an equal footing with those that can be constructed in a finite number of steps. Since antiquity, a majority of mathematicians had carefully avoided the introduction into their arguments of the actual infinite (i.e., of sets containing an infinity of objects conceived as existing simultaneously, at least in thought). Since this attitude persisted until almost the end of the 19th century, Cantor’s work was the subject of much criticism to the effect that it dealt with fictions—indeed, that it encroached on the domain of philosophers and violated the principles of religion. Once applications to analysis began to be found, however, attitudes began to change, and by the 1890s Cantor’s ideas and results were gaining acceptance. By 1900, set theory was recognized as a distinct branch of mathematics.
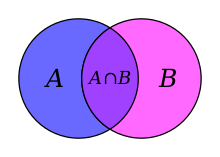
The intersection operation is denoted by the symbol ∩. The set A ∩ B—read “A intersection B” or “the intersection of A and B”—is defined as the set composed of all elements that belong to both A and B. Thus, the intersection of the two committees in the foregoing example is the set consisting of Blanshard and Hixon.
If E denotes the set of all positive even numbers and O denotes the set of all positive odd numbers, then their union yields the entire set of positive integers, and their intersection is the empty set. Any two sets whose intersection is the empty set are said to be disjoint.
FUNCTIONS OF A SET THEORY
Today we’re going to expand on functions within the world of set theory. Similar to previous concepts introduced, the nomenclature for standard functions within sets is slightly different than other branches of math, & therefore requires reviewing. There are quite a few terms to introduce, so let’s jump right in! This first table of function terms below mirrors the idea of domain, range, & output for a standard function:

- A function is injective (a.k.a “one-to-one”) if each element of the codomain mapped to by at most one element of the domain.
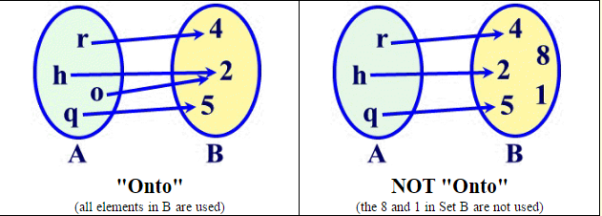
- A function is surjective (a.k.a “onto”) if each element of the codomain is mapped to by at least one element of the domain. (That is, the image and the codomain of the function are equal.)
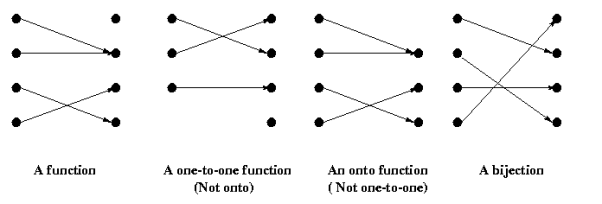
- A function is bijective (a.k.a “one-to-one & onto,” “one-to-one correspondence”) if each element of the codomain is mapped to by exactly one element of the domain.
Limits and continuity concept is one of the most crucial topics in calculus. Both concepts have been widely explained in Class 11 and Class 12.
A limit is defined as a number approached by the function as an independent function’s variable approaches a particular value. For instance, for a function f(x) = 4x, you can say that “The limit of f(x) as x approaches 2 is 8”. Symbolically, it is written as;
Limx→2(4x)=4×2=8
Continuity is another popular topic in calculus. The easy method to test for the continuity of a function is to examine whether a pen can trace the graph of a function without lifting the pen from the paper. When you are doing with precalculus and calculus, a conceptual definition is almost sufficient, but for higher level, a technical explanation is required. You can learn a better and precise way of defining continuity by using limits.
Continuity Definition
A function is said to be continuous at a particular point if the following three conditions are satisfied.
- f(a) is defined
- Limx→af(x) exists
- Limx→a+f(x)=limx→a−f(x)=f(a)
A function is said to be continuous if you can trace its graph without lifting the pen from the paper. But a function is said to be discontinuous when it has any gap in between. Let us see the types discontinuities.
Types of Discontinuity
There are basically two types of discontinuity:
- Infinite Discontinuity
- Jump Discontinuity
Infinite Discontinuity
A branch of discontinuity wherein, a vertical asymptote is present at x = a and f(a) is not defined. This is also called as Asymptotic Discontinuities. If a function has values on both sides of an asymptote, then it cannot be connected, so it is discontinuous at the asymptote.
Jump Discontinuity
A branch of discontinuity wherein limx→a+f(x)≠limx→a−f(x), but both the limits are finite. This is also called simple discontinuity or continuities of first kind.
Positive Discontinuity
A branch of discontinuity wherein a function has a pre-defined two-sided limit at x=a, but either f(x) is undefined at a, or its value is not equal to the limit at a.
Limit Definition
A limit of a function is a number that a function reaches as the independent variable of the function reaches a given value. The value (say a) to which the function f(x) gets close arbitrarily as the value of the independent variable x becomes close arbitrarily to a given value a symbolized as f(x) = A.
Points to remember:
- If limx→a- f(x) is the expected value of f at x = a given the values of ‘f’ near x to the left of a. This value is known as left-hand limit of ‘f’ at a.
- If limx→a+ f(x) is the expected value of f at x = a given the values of ‘f’ near x to the right of a. This value is known as the right-hand limit of f(x) at a.
- If the right-hand and left-hand limits coincide, we say the common value as the limit of f(x) at x = a and denote it by limx→a f(x).
One-Sided Limit
The limit that is based completely on the values of a function taken at x -value that is slightly greater or less than a particular value. A two-sided limit limx→af(x) takes the values of x into account that are both larger than and smaller than a. A one-sided limit from the left limx→a−f(x) or from the right limx→a−f(x) takes only values of x smaller or greater than a respectively.
Properties of Limit
- The limit of a function is represented as f(x) reaches L as x tends to limit a, such that; limx→af(x) = L
- The limit of the sum of two functions is equal to the sum of their limits, such that: limx→a [f(x) + g(x)] = limx→a f(x) + limx→a g(x)
- The limit of any constant function is a constant term, such that, limx→a C = C
- The limit of product of the constant and function is equal to the product of constant and the limit of the function, such that: limx→a m f(x) = m limx→a f(x)
- Quotient Rule: limx→a[f(x)/g(x)] = limx→af(x)/limx→ag(x); if limx→ag(x) ≠ 0
Examples
1). Compute limx→−2(3x2+5x−9)
Solution:
First, use property 2 to divide the limit into three separate limits. Then use property 1 to bring the constants out of the first two. This gives,
Limx→−2(3x2+5x−9)=limx→−2(3x2)+limx→−2(5x)−limx→−2(9)
=3(−2)2+5(−2)−(9)
= -7
2). Find the limits of limx→3 [x(x+2)].
Solution: limx→3 [x(x+2)] = 3(3+2) = 3 x 5 = 15
Differentiability of a real variables :
The derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.
Differentiability of a single variable and its uses:
The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.
The Derivative of a function of a Single Variable We motivate the definition of the derivative of a function of two or more variables as follows. Recall from calculus I, Definition. Derivatives in One Dimension
Let f : D ⊂ R → R and let x0 be an interior point of D. Then f is differentiable at x0 if the limit below exists.
(1) lim x→x0 f(x) − f(x0) x − x0 = f ′ (x0) and the number f ′ (x0) is called the derivative of f at x0.
We also saw that although continuity didn’t guarantee differentiability, the converse was true. That is, differentiability implies continuity.
Theorem 1.
Differentiability Implies Continuity If f is differentiable at x0, then f is continuous at x0.
It turns out that equation (1) can be restated.
Definition. Derivatives in One Dimension - Alternate Definition
Let f : D ⊂ R → R and let x0 be an interior point of D.
Then f is differentiable at x0 if there is a number f ′ (x0) such that (2) lim x→x0 f(x) − f(x0) − (x − x0)f ′ (x0) |x − x0| = 0 and the number f ′ (x0) is called the derivative of f at x0.
We use this definition to create a definition of the derivative for functions of
Several variables. Definition. Derivatives in Higher Dimensions Let f : D ⊂ R n → R
And let P0 be an interior point of D. Then f is differentiable at P0 if there is a vector
f ′ (P0) such that
 lim P→P0 f (P) − f (P0) − # » P0P · f ′ (P0) =0
lim P→P0 f (P) − f (P0) − # » P0P · f ′ (P0) =0
|P − P0|
Uses of differentiability of a single variable:
*In single variable calculus, a function is differentiable at if the following limit exists: This limit exists if and only if In turn, this is true if and only if If we let, this is equivalent to Recall that, as defined above, is the linear approximation to at.
Example 1:
Suppose there is a c∈Rc∈R and a function E:R→RE:R→R, s.t. f(x)=f(a)+c(x−a)+E(x)f(x)=f(a)+c(x−a)+E(x) near aa and limx→aE(x)x−a=0limx→aE(x)x−a=0.
Then:
Limx→af(x)−f(a)x−a−c=limx→af(x)−f(a)−c(x−a)x−a=0limx→af(x)−f(a)x−a−c=limx→af(x)−f(a)−c(x−a)x−a=0
So that means:
f′(x)f′(x) exists and f′(x)=cf′(x)=c. Of course writing f′(x)f′(x) instead of cc before you know this is indeed begging the question.
Example 2:
For a function f:R→Rf:R→R, suppose that there exist a real number AA such that for all xx in some neighbourhood of aa,
f(x)=f(a)+A(x−a)+E(x)f(x)=f(a)+A(x−a)+E(x)
And that
Limx→aE(x)(x−a)=0limx→aE(x)(x−a)=0
,we say that ff is differentiable at aa. If ff is differentiable at aa we define f′(a)f′(a) by
f′(a)=Af′(a)=A
This definition is not circular and is useful since it can be generalized to the case where f:Rn→Rmf:Rn→Rm. In this case AA is a matrix instead of a real number (to be precise, AA is a linear operator
Successive differentiation
Let f be a differentiable function on an interval I. Then the derivative f′ is a function of x and if f′ is differentiable at x, then the derivative of f′ at x is called second derivative of f at x. It is denoted by f″(x) or f(2)(x). Similarly, if f” is differentiable at x , then this derivative is called the 3rd derivative of f and it is denoted by f(3)(x). Proceeding in this way the nth derivative of f is the derivative of the function f(n-1)(x) and it the denoted by f(n)(x).
If y = f(x) then f(n) (x) is denoted by dn y/ dxn or Dn y or yn or yn and
F(n) (x)= lim h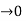 f(n-1) (x+h) – f(n-1) (x )/ h
f(n-1) (x+h) – f(n-1) (x )/ h
Successive nth derivative of elementary functions ie., trigonometric
Find the nth derivative of sin3 x
Sol: we know that sin 3x= 3sin x 4sin3 x = sin3x = 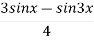
Differentiate n times w.r.t x,
 ( sin3 x) =
( sin3 x) = 
 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Example 2:
Find the nth derivative of sin 5x. Sin 3x.?
Sol: let y = sin 5x.sin 3x=  ( sin 5x.sin 3x)
( sin 5x.sin 3x)
⇒y=  ( cos 2x - cos8x)
( cos 2x - cos8x)
⇒ y= ( cos 2x- cos8x )
( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = 
 ( cos 2x - cos8x )
( cos 2x - cos8x )
⇒ yn =  ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Successive n th derivative of nth elementary function ie., exponential
If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Example 2:
If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol : y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
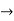 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
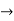 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)  (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
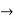 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Successive differentiation of nth derivative of elementary functions ie., logarithmic
Example :
If Y 2) = log( x +
2) = log( x + 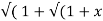 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y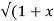 2) = log( x +
2) = log( x + 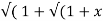 2) )
2) )
Differentiating w.r.to x.,
y.1/ 2 2 .2x+
2 .2x+ 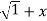 2. Y1.
2. Y1.
=(1+x ) y +xy = 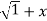 . 1/x
. 1/x 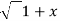 2 .
2 .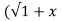 2) +x/
2) +x/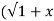 2 =1
2 =1
Successive differentiation of nth derivative of elementary functions ie., logarithmic
Example :
If Y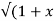 2) = log( x +
2) = log( x + 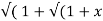 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y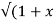 2) = log( x +
2) = log( x + 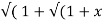 2) )
2) )
Differentiating w.r.to x.,
y.1/ 2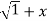 2 .2x+
2 .2x+ 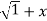 2. Y1.
2. Y1.
=(1+x ) y +xy = 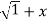 . 1/x+
. 1/x+ 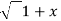 2 .
2 .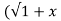 2) +x/
2) +x/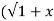 2 =1
2 =1
In calculus, the general Leibniz rule named after Gottfried Wilhelm Leibniz, generalizes the product rule (which is also known as "Leibniz's rule"). It states that if f and g are n-times differentiable functions, then the product fg is also n-times differentiable and its nth derivative is given by
(fg)n =  k=0n (nk) f(n-k).g(k)
k=0n (nk) f(n-k).g(k)
where (nk) = n /k
/k 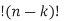 is the binomial coefficient and f(j) denotes the jth derivative of f and f(0) = f
is the binomial coefficient and f(j) denotes the jth derivative of f and f(0) = f
In particular.
The rule can be proved by using the product rule and mathematical induction
Maclaurin’s Series Expansions
Statement:-
Maclaurin’s series of f(x) at x = 0 is given by,
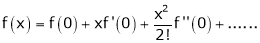
Expansion of some standard functions
i) f(x) = ex then
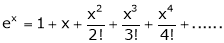
Proof:-
Here
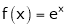

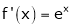
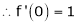
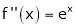
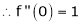
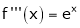
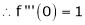
 By Maclaurin’s series we get,
By Maclaurin’s series we get,
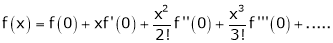
i.e. 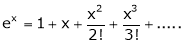
Note that
- Replace x by –x we get
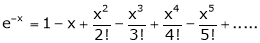
2. f(x) = sin x then

Proof:
Let (x) = sin x
Then by Maclaurin’s series,
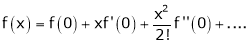 … (1)
… (1)
Since
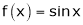
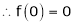
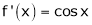
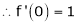
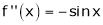
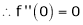
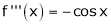

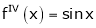
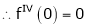
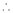 By equation (i) we get,
By equation (i) we get,
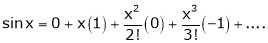
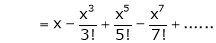
3. 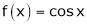 Then
Then
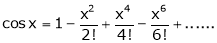
Proof:
Let f(x) = cos x
Then by Maclaurin’s series,
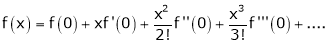 … (1)
… (1)
Since
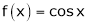

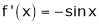
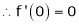

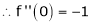
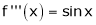
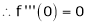
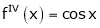
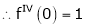
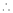 From Equation (1)
From Equation (1)
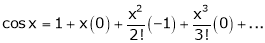
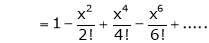
4. 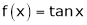 then
then
Proof:
Here f(x) = tan x
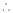 By Maclaurin’s expansion,
By Maclaurin’s expansion,
 … (1)
… (1)
Since
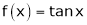
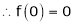

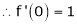


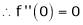
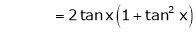

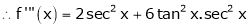
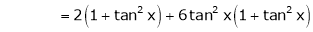
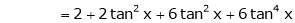
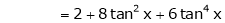
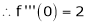
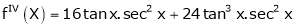
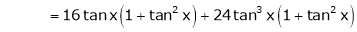

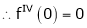
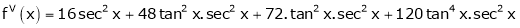
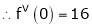 …..
…..
 By equation (1)
By equation (1)
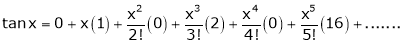
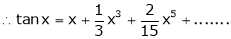
5. 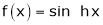 Then
Then
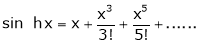
Proof:-
Here f(x) = sin hx.
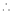 By Maclaurin’s expansion,
By Maclaurin’s expansion,
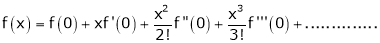 (1)
(1)
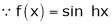
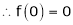
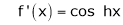
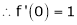

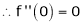
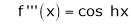
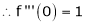
 By equation (1) we get,
By equation (1) we get,
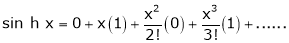
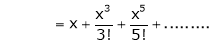
6. 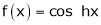 . Then
. Then
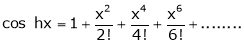
Proof:-
Here f(x) = cos hx
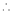 By Maclaurin’s expansion
By Maclaurin’s expansion
 (1)
(1)
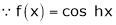
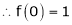

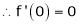

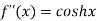


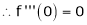
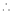 By equation (1)
By equation (1)

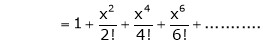
7. f(x) = tan hx
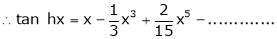
Proof:
Here f(x) = tan hx
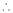 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
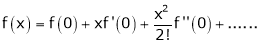 … (1)
… (1)
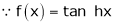
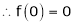
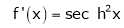
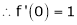
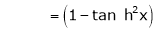

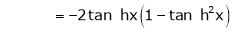

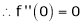
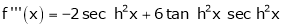
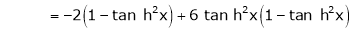
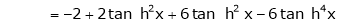
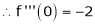

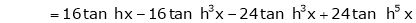
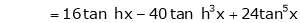
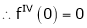
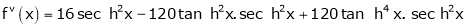

 By equation (1)
By equation (1)
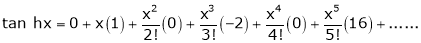
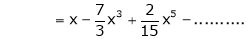
8. 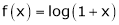 then
then
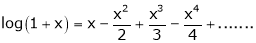
Proof:-
Here f(x) = log (1 + x)
 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
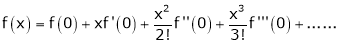 … (1)
… (1)
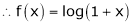
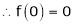
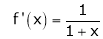
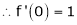
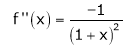
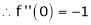
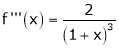
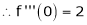
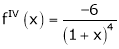

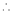 By equation (1)
By equation (1)


9. 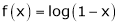
In above result we replace x by -x
Then
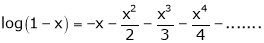
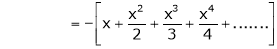
10. Expansion of tan h-1x
We know that
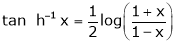


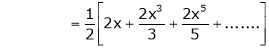
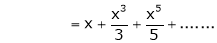
Thus

11. Expansion of (1 + x)m
Proof:-
Let f(x) = (1 + x)m
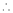 By Maclaurin’s series.
By Maclaurin’s series.
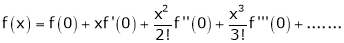 … (1)
… (1)
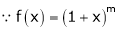
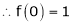
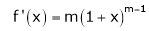
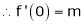
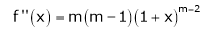
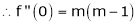
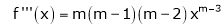
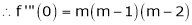
 By equation (1) we get,
By equation (1) we get,
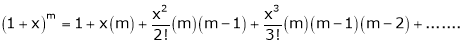
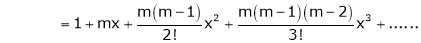
Note that in above expansion if we replace m = -1 then we get,

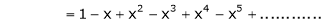
Now replace x by -x in above we get,
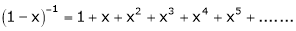
Expand by, Maclaurin’s theorem
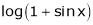
Solution:
Here f(x) = log (1 + sin x)
 By Maclaurin’s Theorem,
By Maclaurin’s Theorem,
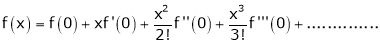 … (1)
… (1)
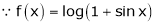
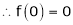
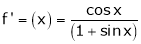
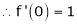
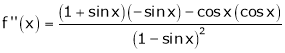
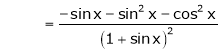
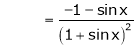
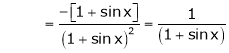
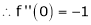
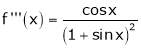
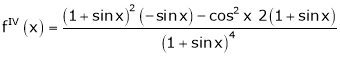
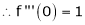
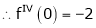 ……..
……..
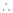 equation (1) becomes,
equation (1) becomes,

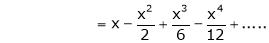
Expand by Maclaurin’s theorem,
Log sec x
Solution:
Let f(x) = log sec x
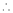 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
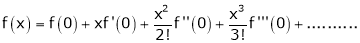 (1)
(1)
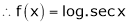
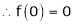
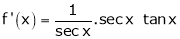
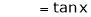

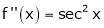
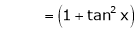
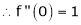
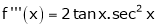
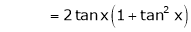
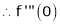
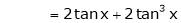
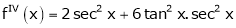



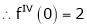
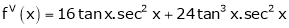
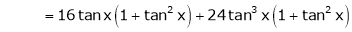
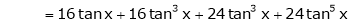
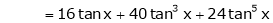

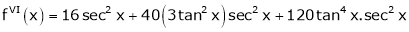
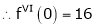
 By equation (1)
By equation (1)
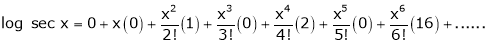
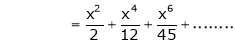
Prove that 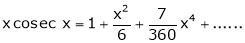
Solution:
Here f(x) = x cosec x
= 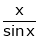
Now we know that
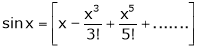
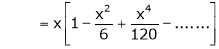
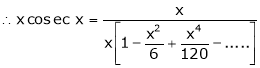
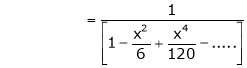
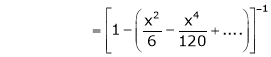
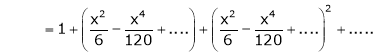
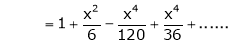
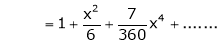
Expand 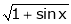 upto x6
upto x6
Solution:
Here 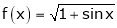
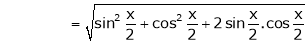
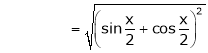
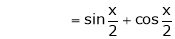
Now we know that
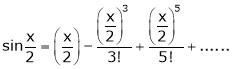 … (1)
… (1)
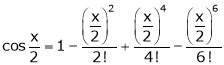 … (2)
… (2)
Adding (1) and (2) we get
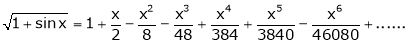
Show that 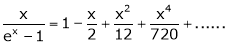
Solution:
Here 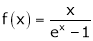
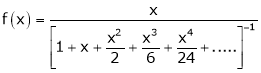
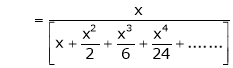
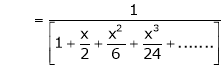
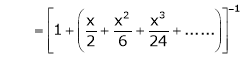
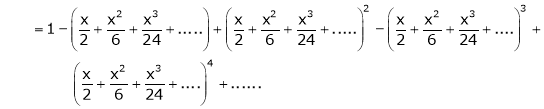
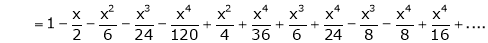
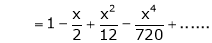
Thus
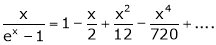
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
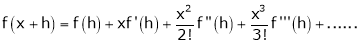
b) The expansion of f(x+h) in ascending power of h is
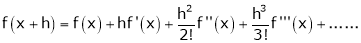
c) The expansion of f(x) in ascending powers of (x-a) is,

Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions
Expand 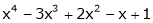 in power of (x – 3)
in power of (x – 3)
Solution:
Let 
Here a = 3
Now by Taylor’s series expansion,
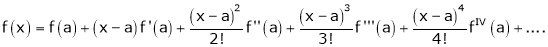 … (1)
… (1)

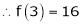
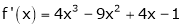
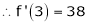
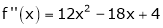
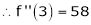

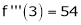
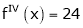
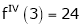
 equation (1) becomes.
equation (1) becomes.
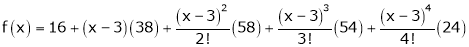
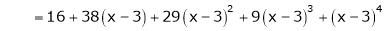
Using Taylors series method expand
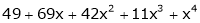 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 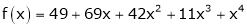
a = -2
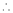 By Taylors series,
By Taylors series,
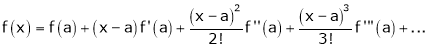 … (1)
… (1)
Since

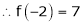
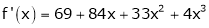
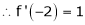
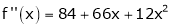
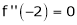
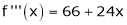
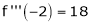
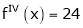
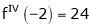 ,
, 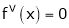 , …..
, …..
Thus equation (1) becomes
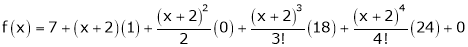
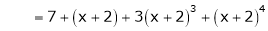
Expand 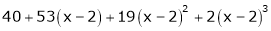 in ascending powers of x.
in ascending powers of x.
Solution:
Here
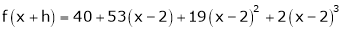
i.e. 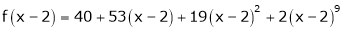
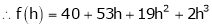
Here h = -2
 By Taylors series,
By Taylors series,
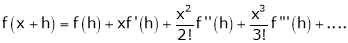 … (1)
… (1)
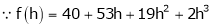
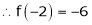
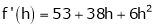
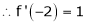

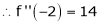
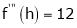
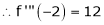

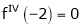
 equation (1) becomes,
equation (1) becomes,
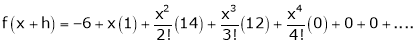
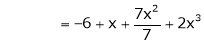
Thus
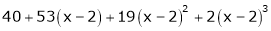
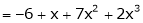
Expand 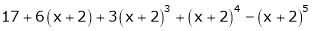 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
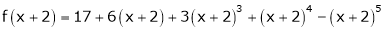
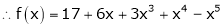
i.e. 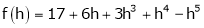
Here
h = 2
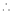 By Taylors series
By Taylors series
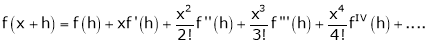 … (1)
… (1)


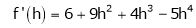
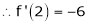
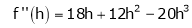
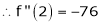
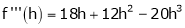
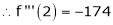
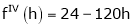
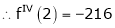
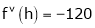
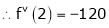
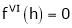
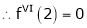
 By equation (1)
By equation (1)
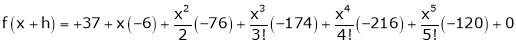
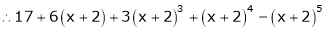
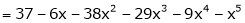
L – Hospital rule for 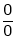 and
and 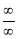
Statement:
If 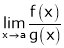 takes either
takes either 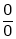 or
or 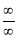
Indeterminate form, then
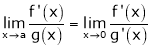 Provided limit is exist
Provided limit is exist
If 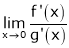 again takes either
again takes either 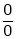 or
or 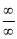 .
.
Then 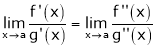 ; limit is exist
; limit is exist
We continue the procedure until the limit is exist.
Exercise 1
Evaluate 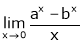
Solution:
Let
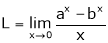 …
… 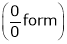
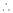 By L – Hospital rule,
By L – Hospital rule,
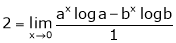
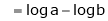
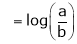
Exercise 2
Evaluate 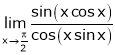
Solution:
Let
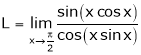 …
… 
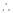 By L – Hospital rule
By L – Hospital rule
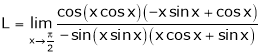
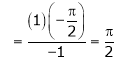
Exercise 3
Evaluate 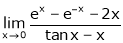
Solution:
Let
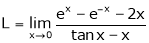 …
… 
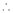 By L – Hospital rule
By L – Hospital rule
 …
… 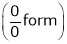
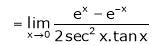 …
… 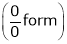
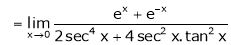
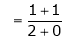

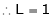
Find the value of a, b if 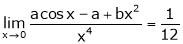
Solution:
Let
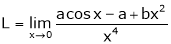 …
… 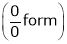
 By L – Hospital rule
By L – Hospital rule
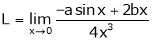 …
… 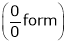
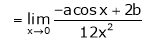 …
… 
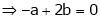 … (1)
… (1)
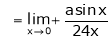 …
… 
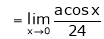
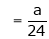
But 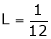
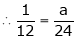
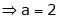
 From equation (1)
From equation (1)
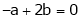
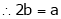
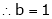
Evaluate 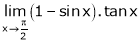
Solution:
Let
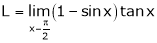 …
… 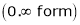
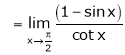 …
… 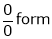
 (By L – Hospital Rule)
(By L – Hospital Rule)
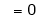
Evaluate 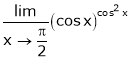
Solution:
Let
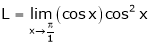 … 0o form
… 0o form
Taking log on both sides we get,
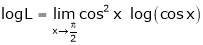 …
… 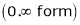
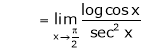 …
… 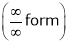
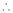 By L – Hospital Rule
By L – Hospital Rule
i.e. 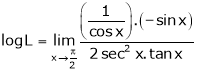

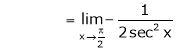

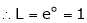
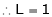
Evaluate 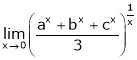
Solution:
Let
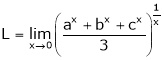 …
… 
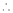 Taking log on both sides,
Taking log on both sides,

 …
… 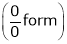
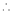 By L – Hospital rule,
By L – Hospital rule,
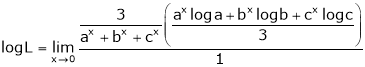
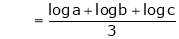
i.e. 
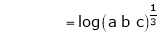
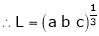
Evaluate 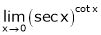
Solution:
Let
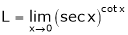 …
… 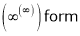
 Taking log on both sides, we get
Taking log on both sides, we get
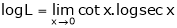
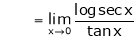 …
… 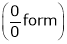
 By L – Hospital Rule,
By L – Hospital Rule,
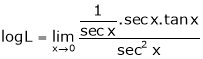
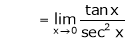
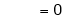
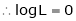

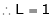
Reference Books
1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008
2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007
3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.
4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson