UNIT -1
ERROR ANALYSIS
UNCERTAINTIES IN MEASUREMENTS
Measurement of any physical quantity involves comparison with a certain basic, arbitrarily chosen, internationally accepted reference standard known as unit.
Uncertainty of measurement is the doubt that exists about the result of any measurement. You might think that well-made rulers, clocks and thermometers should be trustworthy and give the right answers. But for every measurement even you take the case of the most careful one, a margin of doubt is always there.
However, all measurements have some degree of uncertainty that may come from a variety of sources. The process of evaluating the uncertainty associated with a measurement result is often called uncertainty analysis or error analysis.
When we make a measurement, we generally assume that some exact or true value exists based on how we define what is being measured. While we may never know this true value exactly, we attempt to find this ideal quantity to the best of our ability with the time and resources available. As we make measurements by different methods, or even when making multiple measurements using the same method, we may obtain slightly different results.
If you measure the same object two different times, the two measurements may not be exactly the same. The difference between two measurements is called a variation in the measurements.
Another word for this variation - or uncertainty in measurement - is "error." This "error" is not the same as a "mistake." It does not mean that you got the wrong answer. The error in measurement is a mathematical way to show the uncertainty in the measurement. It is the difference between the result of the measurement and the true value of what you were measuring. We seek to minimize uncertainty and hence error to the extent possible.
It is important not to confuse the terms ‘uncertainty’ and ‘error’.
Uncertainty is a quantification of the doubt about the measurement result.
Or
Uncertainty means the range of possible values within which the true value of the measurement lies.
When you repeat a measurement you often get different results. There is an uncertainty in the measurement that you have taken. It is important to be able to determine the uncertainty in measurements so that its effect can be taken into consideration when drawing conclusions about experimental results.
Error means the difference between a measured value and the true value for a measurement.
SOURCES AND ESTIMATION OF ERRORS
Types of Errors: The errors in measurement can be broadly classified as
- Systematic errors
- Random errors
- Least count error
- Systematic Errors
The systematic errors are those errors that tend to be in one direction, either positive or negative. Basically, these are the errors whose causes are known.
a) Instrumental Errors
These errors arise from the errors due to imperfect design or calibration of the measuring instrument, zero error in the instrument etc.
Example: Temperature graduations of a thermometer may be inadequately calibrated. It may read 103 °C at the boiling point of water at STP whereas it should read 100 °C.
In a vernier calliper the zero mark of vernier scale may not coincide with the zero mark of the main scale
b) Imperfection in experimental technique or procedure
To determine the temperature of a human body, a thermometer placed under the armpit will always give a temperature lower than the actual value of the body temperature.
Other external conditions such as changes in humidity, temperature, wind velocity, etc. during the experiment may systematically affect the measurement.
c) Personal errors
Such errors arise due to an individual’s bias, lack of proper setting of the apparatus or individual’s carelessness in taking observations without observing proper precautions, etc.
For example, if you, by habit, always hold your head a bit too far to the right while reading the position of a needle on the scale, you will introduce an error due to parallax.
2. Random Errors
The random errors are those errors, which occur irregularly and hence are random with respect to sign and size. These can arise due to random and unpredictable fluctuations in experimental conditions (e.g. Unpredictable fluctuations in temperature, voltage supply, mechanical vibrations of experimental set-ups, etc.), personal (unbiased) errors by the observer taking readings, etc.
For example, when the same person repeats the same observation, it is very likely that he may get different readings every time.
3. Least Count Error
Least count is the smallest value that can be measured by the measuring instrument. Least count error is the error associated with the resolution of the instrument.
For example, a vernier callipers has the least count as 0.01 cm; a spherometer may have a least count of 0.001 cm.
Least count error belongs to the category of random errors but within a limited size; it occurs with both systematic and random errors.
ABSOLUTE ERROR, RELATIVE ERROR AND PERCENTAGE ERROR
Absolute Error
Let the values obtained in several measurements are a1 , a2 , a3……..an The arithmetic mean of these values is taken as the best possible value of the quantity under the given conditions of measurement as a mean = (a1 + a2 + a3 … + an )/n
The magnitude of the difference between the true value of the quantity and the individual measurement value is called the absolute error of the measurement.
This is denoted by |Δa|.
Note: In the absence of any other method of knowing true value, we considered arithmetic mean as the true value.
Then the errors in the individual measurement values are
Δa1 = amean – a1
Δa2 = amean – a2
.... .... ....
.... .... ....
Δan = amean – an
The Δa calculated above may be positive in certain cases and negative in Some other cases. But absolute error |Δa| will always be positive.
Mean Absolute Error
It is the arithmetic mean of the magnitude of absolute errors in all the measurement of the quantity. It is generally represented by Δamean. If we do a single measurement, the value we get may be in the range amean ± Δamean
So a = amean ± Δamean
Relative Error
The relative error is the ratio of the mean absolute error Δamean to the
Mean value amean of the quantity measured.
i.e., Relative error = Δamean / a mean
Percentage Error
Percentage error,
δa = (Δamean /amean ) × 100%
Combination of Errors
(a) Error of a sum or a difference
When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
Z = A + B
We have by addition, Z ± ΔZ = (A ± ΔA) + (B ± ΔB).
The maximum possible error in Z
ΔZ = ΔA + ΔB
For the difference Z = A – B, we have
Z ± Δ Z = (A ± ΔA) – (B ± ΔB) = (A – B) ± ΔA ± ΔB
Or, ± ΔZ = ± ΔA ± ΔB
The maximum value of the error ΔZ is again ΔA + ΔB.
(b) Error of a product or a quotient
When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.
Suppose Z = AB and the measured values of A and B are A ± ΔA and B ±ΔB. Then
Z ± ΔZ = (A ± ΔA) (B ± ΔB) = AB ± B ΔA ± A ΔB ± ΔA ΔB.
Dividing LHS by Z and RHS by AB we have,
1 ± (ΔZ/Z) = 1 ± (ΔA/A) ± (ΔB/B) ± (ΔA/A)(ΔB/B).
Since ΔA and ΔB are small, we shall ignore their product.
Hence the maximum relative error
ΔZ/ Z = (ΔA/A) + (ΔB/B).
(c) Error in case of a measured quantity raised to a power
The relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.
Suppose Z = A2 Then,
ΔZ/Z = (ΔA/A) + (ΔA/A) = 2 (ΔA/A).
Hence, the relative error in A2 is two times the error in A.
In general, if Z = (Ap Bq )/Cr
Then,
ΔZ/Z = p (ΔA/A) + q (ΔB/B) + r (ΔC/C).
SIGNIFICANT FIGURES
Significant figures in the measured value of a physical quantity tell the number of digits in which we have confidence. Larger the number of significant figures obtained in a measurement, greater is the accuracy of the measurement. The reverse is also true.
Important Rules of counting significant figures
- All the non-zero digits are significant.
- All the zeros between two non-zero digits are significant, no matter where the decimal point is, if at all.
- If the number is less than 1, the zero(s) on the right of decimal point but to the left of the first non-zero digit are not significant.
- The terminal or trailing zero(s) in a number without a decimal point are not significant. [Thus 123 m = 12300 cm = 123000 mm has three significant figures, the trailing zero(s) being not significant.]
- The trailing zero(s) in a number with a decimal point are significant. The numbers 3.500 or 0.06900 have four significant figures each.
- For a number greater than 1, without any decimal, the trailing zero(s) are not significant.
- For a number with a decimal, the trailing zero(s) are significant.
Rules for Arithmetic Operations with Significant Figures
(1) In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.
(2) In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.
Cautions to remove ambiguities in determining number of significant figures
- Change of units should not change number of significant digits. Example, 4.700m = 470.0 cm = 4700 mm. In this, first two quantities have 4 but third quantity has 2 significant figures.
- Use scientific notation to report measurements. Numbers should be expressed in powers of 10 like a x 10b where b is called order of magnitude. Example, 4.700 m = 4.700 x 102 cm = 4.700 x 103 mm = 4.700 x 10-3 In all the above, since power of 10 are irrelevant, number of significant figures are 4.
- Multiplying or dividing exact numbers can have infinite number of significant digits. Example, radius = diameter / 2. Here 2 can be written as 2, 2.0, 2.00, 2.000 and so on.
Rounding Off the Uncertain Digits
(i) If the digit dropped is less than 5, then the preceding digit is left unchanged.
(ii) If the digit to be dropped is more than 5, then the preceding digit is raised by one.
(iii) If the digit to be dropped is 5 followed by digits other than zero, then the preceding digit is raised by one.
(iv) If the digit to be dropped is 5 or 5 followed by zeroes, then the preceding digit is left unchanged, if it is even.
(v) If the digit to be dropped is 5 or 5 followed by zeroes then the preceding digit is raised by one, if it is odd.
Rules for Determining the Uncertainty in the Results of Arithmetic
(i) Calculations Rules for determining the uncertainty in the results of arithmetic calculations can be understood with the following examples:
Example
Suppose,
l = 16.2 ± 0.1 cm = 16.2 cm ± 0.6 % and
b = 10.1 ± 0.1 cm= 10.1 cm ± 1 %
Then, the error of the product of two experimental values, using the combination of errors rule, will be
Lb = 163.62 cm2 + 1.6% = 163.62 + 2.6 cm2
This leads us to quote the final result as
Lb = 164 + 3 cm2
Here, 3 cm2 is the uncertainty or error in the estimation of area of rectangular sheet.
(ii) If a set of experimental data is specified to n significant figures, a result obtained by combining the data will also be valid to n significant figures.
Example: 12.9 g – 7.06 g, both specified to three significant figures, can’t properly be evaluated as 5.84 g but only as 5.8 g, as uncertainties in subtraction or addition combine in a different fashion such as smallest number of decimal places rather than the number of significant figures in any of the number added or subtracted.
(iii) The relative error of a value of number specified to significant figure depends not only on n but also on the number itself.
Example: the accuracy in measurement of mass 1.02 g is ± 0.01 g
Whereas another measurement 9.89 g is also accurate to ± 0.01 g.
The relative error in 1.02 g is = (± 0.01/1.02) × 100 % = ± 1%
Similarly, the relative error in 9.89 g is = (± 0.01/9.89) × 100 % = ± 0.1 %
PRECISION AND ACCURACY
Precision refers to the amount of scatter in a set of numbers presumed to measure the same quantity. For example, suppose you repeatedly placed the same coin on an analytical balance. The scatter in your results would define the precision of the measurement. Accuracy refers to the degree to which the set of numbers represents the "true" value of the quantity. If, in the above example, the balance were not properly levelled, it might give good precision, but the value could be wrong, thereby leading to poor accuracy.
Further, there is important aspect of reporting measurement. It should be consistent, systematic and revealing in the context of accuracy and precision.
Accuracy is a measure of how close the result of the measurement comes to the "true", "actual", or "accepted" value. It is associated with systematic error.
Precision of measurement is related to the ability of an instrument to measure values in greater details. The precision of a measuring instrument is determined by the smallest unit to which it can measure. The precision is said to be the same as the smallest fractional or decimal division on the scale of the measuring instrument. It is associated with random error.
Accuracy of a measurement is how close the measured value is to the true value.
Example Suppose you weigh a box and noted 3.1 kg but its known value is 9 kg, then your measurement is not accurate.
Precision is the resolution or closeness of a series of measurements of a same quantity under similar conditions.
Suppose you weigh the same box five times and get close results like 3.1, 3.2, 3.22, 3.4, and 3.0 then your measurements are precise.
Let us take a look on another example for clarity. If the true value of a certain length is 3.678 cm and two instruments with different resolutions, up to 1 (less precise) and 2 (more precise) decimal places respectively are used. If first measures the length as 3.5 and the second as 3.38 then the first has more accuracy but less precision while the second has less accuracy and more precision.
Accuracy and Precision are two independent terms. You can be very accurate but non-precise, or vice-versa.
Measurements of units revolve around accuracy and precision, that’s why we find our experiment readings to be in decimal form.
PARENT DISTRIBUTION - MEAN AND STANDARD DEVIATION OF DISTRIBUTION
Parent Distributions Measurement of any physical quantity is always affected by uncontrollable random processes. These produce a statistical scatter in the values measured.
The parent distribution for a given measurement gives the probability of obtaining a particular result from a single measure.
It is fully defined and represents the idealized outcome of an infinite number of measures, where the random effects on the measuring process are assumed to be always the same.
Moments of Parent Distribution
The parent distribution is characterized by its moments:
Parent probability distribution p(x)
Mean: first moment μ = ∫x p(x)dx
Variance: second moment Var(x) = ∫(x−μ)2p(x)dx
Standard Deviation (Sigma): σ = √Var(x)
σ is the standard deviation, but is also known as the “dispersion” or “r.m.s. Dispersion”
•μ measures the “center” and σ measures the “width” of the parent distribution.
Poisson distribution
The Poisson distribution is derived as a limit of the “binomial distribution” based on the fact that time can be divided up into small intervals such that the probability of an event in any given interval is arbitrarily small. If n is the number of counts observed in one δt bin, then
PP(n) =(μn /n! ) e−μ
Properties:
∞∑n=0 pP(n) = 1
Asymmetric about μ;
Mode≤μ
Mean value per bin:μ. μ need not be an integer.
Variance: μ
Standard deviation: σ=√μ
Implies mean/width=μ/√μ=√μ→“Square root of n statistics”
The Poisson distribution is the proper description of a uniform counting process for small numbers of counts. For larger numbers (n&30), the Gaussian distribution is a good description and is easier to compute.
Gaussian Probability Distribution
The Gaussian, or “normal,” distribution is the limiting form of the Poisson distribution for large μ(&30) Probability distribution:
PG(x) =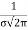 exp [ -
exp [ - 
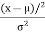 ]
]
Properties:
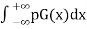 =1
=1
“Bell-shaped” curve; symmetric about mode at μ
Mean value :μ (=median and mode)
Variance: σ2
Full Width Half Maximum= 2.355σ
Then σ=√μ
Importance: The “central limit theorem” of Gauss demonstrates that a Gaussian distribution applies to any situation where a large number of independent random processes contribute to the result. This means it is a valid statistical description of an enormous range of real-life situations. Much of the statistical analysis of data measurement is based on the assumption of Gaussian distributions.
SAMPLE DISTRIBUTIONS- MEAN AND STANDARD DEVIATION OF DISTRIBUTION
A sampling distribution is a probability distribution of a statistic obtained from a larger number of samples drawn from a specific population. The sampling distribution of a given population is the distribution of frequencies of a range of different outcomes that could possibly occur for a statistic of a population.
In statistics, a population is the entire pool from which a statistical sample is drawn. A population may refer to an entire group of people, objects, events, hospital visits, or measurements.
It describes a range of possible outcomes that of a statistic, such as the mean or mode of some variable, as it truly exists a population.
The majority of data analyzed by researchers are actually drawn from samples, and not populations.
A population or one sample set of numbers will have a normal distribution. However, because a sampling distribution includes multiple sets of observations, it will not necessarily have a bell-curved shape.
The distribution of sample statistics is called sampling distribution.
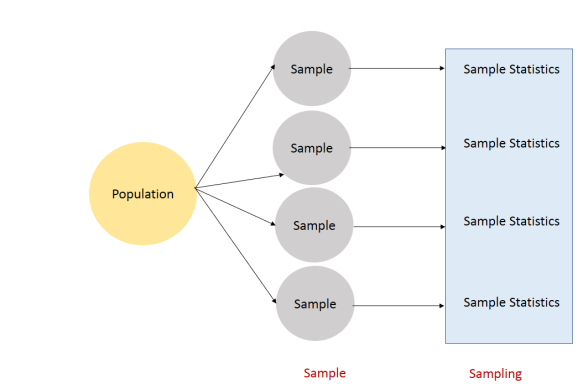
Suppose that a sample of size sixteen (N=16) is taken from some population. The mean of the sixteen numbers is computed. Next a new sample of sixteen is taken, and the mean is again computed. If this process were repeated an infinite number of times, the distribution of the now infinite number of sample means would be called the sampling distribution of the mean.
Sampling Distribution of the Mean
Suppose we draw all possible samples of size n from a population of size N. Suppose further that we compute a mean score for each sample. In this way, we create a sampling distribution of the mean.
We know the following about the sampling distribution of the mean. The mean of the sampling distribution (μx) is equal to the mean of the population (μ). And the standard error of the sampling distribution (σx) is determined by the standard deviation of the population (σ), the population size (N), and the sample size (n). These relationships are shown in the equations below:
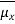 = μ
= μ
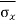 = [σ /
= [σ / ] *
] *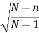
In the standard error formula, the factor 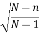 is called the finite population correction or fpc. When the population size is very large relative to the sample size, the fpc is approximately equal to one; and the standard error formula can be approximated by:
is called the finite population correction or fpc. When the population size is very large relative to the sample size, the fpc is approximately equal to one; and the standard error formula can be approximated by:
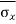 = [σ /
= [σ /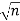 ]
]
Example: The mean and standard deviation of the tax value of all vehicles registered in a certain state are μ=15,575Rs and σ=4200Rs. Suppose random samples of size 100 are drawn from the population of vehicles. What are the mean μX¯ and standard deviation σX¯ of the sample mean X¯?
Solution
Since n=100
Using above the formulas
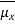 = μ =15,575Rs
= μ =15,575Rs
And
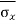 = [σ /
= [σ /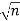 ] = 4200 /
] = 4200 /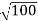 =420 Answer
=420 Answer
AVERAGE ERROR or MEAN ERROR
The mean error usually refers to the average of all the errors in a set. An “error” in this context is an uncertainty in a measurement, or the difference between the measured value and true/correct value. The more formal term for error is measurement error also called observational error.
The mean error usually results in a number that isn’t helpful because positives and negatives cancel each other out. For example, two errors of +100 and -100 would give a mean error of zero:
Mean = sum of all values/number in the set
= (+100 + -100) / 2
= 0 / 2 = 0.
Zero implies that there is no error, when that’s clearly not the case for this example.
Use the mean absolute error (MAE) instead. The MAE uses absolute values of errors in the calculations, resulting in average errors that make more sense.
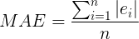
Or
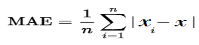
The mean absolute error is usually used in experiments instead of the informal “mean error.”
The mean absolute error (MAE) is defined as the sum of the absolute value of the differences between all the expected values and predicted values, divided by the total number of predictions. In equation form, it looks like this:
Let us look at example to understand it in better way
Example: How do we calculate the mean absolute error?
Expected value | Predicted Value | Error |
5 | 10 | 5 |
11 | 19 | 8 |
37 | 32 | -5 |
9 | 9 | 0 |
21 | 30 | 9 |
48 | 43 | -5 |
33 | 21 | -12 |
25 | 22 | -3 |
12 | 15 | 3 |
MAE= (|5|+|8|+|-5|+|0|+|9|+|-5|+|-12|+|-3|+|3|)/9
= (5+8+5+0+9+5+12+3+3)/9 = 50/9 =~ 5.55
You might be wondering why we use absolute values. This is important to take into consideration the fact that we have two types of errors:
- In some cases the predicted value is lower than the expected value.
- In some cases the predicted value is higher than the expected value.
The absolute value ensures that both types contribute to the overall error. Without it, the positive and negative errors would cancel each other. This is bad: your regression model might perform terribly and still return a very low overall error.
To illustrate this point, repeat the calculation for total error using the data in the table, but this time don't use the absolute values:
Total Error = (5 + 8+ -5 + 0 + 9 + -5 + -12 + -3 + 3)/9 = 0
Yes, a total value of 0 despite making several mistakes. MAE is a very simple and useful metric for error
R.M.S ERROR
Root- mean -square (RMS) error, also known as RMS deviation, is a frequently used measure of the differences between values predicted by a model or an estimator and the values actually observed. These individual differences are called residuals when the calculations are performed over the data sample that was used for estimation, and are called prediction errors when computed out-of-sample. The differences between values occur because of randomness or because the estimator doesn’t account for information that could produce a more accurate estimate.
The use of RMSE is very common, and it is considered an excellent general-purpose error metric for numerical predictions.
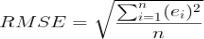
n the number of observations available for analysis.
RMSE is a good measure of accuracy, but only to compare prediction errors of different models.
RMSE can be clearer with the following example
Step 1: Square the error values
Error | Squared Error |
5 | 25 |
8 | 64 |
-5 | 25 |
0 | 0 |
9 | 81 |
-5 | 25 |
-12 | 144 |
-3 | 9 |
3 | 9 |
Step 2: Sum the squared errors and divide the result by the number of examples (calculate the average)
MSE = (25 + 64 + 25 + 0 + 81 + 25 + 144 + 9 + 9)/9 =~ 42.44
Step 3: Calculate the square root of the average
RMSE = 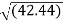 =~ 6.51
=~ 6.51
PROBABLE ERROR
Probable error is the coefficient of correlation that supports in finding out about the accurate values of the coefficients.
It also helps in determining the reliability of the coefficient.
The calculation of the correlation coefficient usually takes place from the samples. These samples are in pairs. The pairs generally come from a very large population.
The correlation coefficient for a population is usually based on the knowledge and the sample relating to the correlation coefficient. Therefore, probable error is the easy way to find out or obtain the correlation coefficient of any population. Hence, the definition is:
Probable Error = 0.674 × 1−r2 /√N
Here, r = correlation coefficient of ‘n’ pairs of observations for any random sample and N = Total number of observations.
Conditions to find Probable Error
We can find the probable error if and only if the given below conditions are taken care of.
- The data that we have must be a bell-shaped curve. This means that the data has to give us a normal frequency curve
- It is important to take the probable error for measuring the statistics from the sample only
- It is compulsory that the sample items are taken off in an unbiased manner and must remain independent of each other’s value
Question: Find the probable error. Assume that the correlation coefficient is 0.8 and the pairs of samples are 25.
Solution: We will use the most common method to calculate the outcome of the following.
Here, r = 0.8 and n = 25. We know that,
Probable Error = 0.674 × 1−r2 /√N
So, on putting the values:
Probable Error = 0.674 × {(1 – (0.8)2 )/√25}
= 0.674 × {(1 – 0.64)/5}
= 0.674 × (0.36/5)
≈ 0.0486
Therefore, the probable error is: 0.0486.
Probable Limit
To get the upper limit and the lower limit, all we need to do is respectively add and subtract the value of probable error from the value of ‘r.’ This is exactly where the value of correlation of coefficient lies.
ρ (rho) = r ± P.E.
Here, the value of rho is nothing but the correlation coefficient of a population. This is also the limit of the correlation of coefficient.
Probable Error = 2/3 SE where, S.E is Standard Error of Correlation Coefficient
Standard Error = (1-r2)/√N
Standard Error is basically the standard deviation of any mean. It is the sampling distribution of the standard deviation. The standard error is generally used to refer to any sort of estimate belonging to the standard deviation. Therefore, we use probable error to calculate and check the reliability associated with the coefficient.
Example If the value of r = 0.7 and that of n = 64, then find the P. E. Of the correlation of coefficient. Furthermore, find the limits for the population correlation coefficient.
Solution: Here, we have to calculate the probable error.
Given, r = 0.7 and n = 64. We know that,
P. E. = 0.674 × {(1-r2 )/√N}
= 0.6745 × {(1 – (0.7)2 )/√64}
= 0.6745 × 0.06375
≈ 0.043
Therefore, the P.E. Is 0.043. Now, we have to calculate the limits of the population correlation coefficient. We use the formula,
Probable Limit- ρ (rho) = r ± P.E.r
Hence, we get, (0.7 ± 0.043) i.e. (0.743, 0.657).
PROPAGATION OF ERROR
Propagation of Error (or Propagation of Uncertainty) is defined as the effects on a function by a variable's uncertainty. It is a calculus derived statistical calculation designed to combine uncertainties from multiple variables, in order to provide an accurate measurement of uncertainty.
In statistics, propagation of uncertainty (or propagation of error) is the effect of variables uncertainties on the uncertainty of a function based on them.
Error propagation (or propagation of uncertainty) is what happens to measurement errors when you use those uncertain measurements to calculate something else.
For example, you might use velocity to calculate kinetic energy, or you might use length to calculate area. When you use uncertain measurements to calculate something else, they propagate To take this propagation into account, use one of the following formulas in your experiments.
Error Propagation
- Addition or Subtraction Formula
- Multiplication or Division formula
- Measured Quantity Times Exact Number formula
- General formula
- Power formula
1. Addition or Subtraction
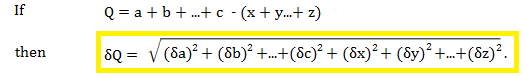
Where:
- a,b,c are positive measurements
- x,y,z are negative measurements
- δ is the error associated with each measurement (the absolute error). δa is the uncertainty associated with measurement a, δb is the uncertainty associated with measurement b, and so on.
Example: Let’s say you measured your height (a) as 2.00 ± 0.03 m. Your waistband (b) is 0.88 ± 0.04 m from the top of your head, which means your pant length P would be p = H – w = 2.00 m – 0.88 m = 1.12 m. The uncertainty, using the addition formula is: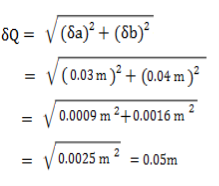
2. Multiplication or Division formula
When calculating errors, there is no difference between multiplication and division.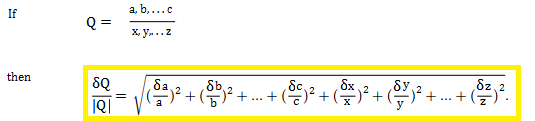
3. Power formula
If n is an exact number and Q = xn, then
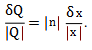
4. Measured Quantity Times Exact Number formula
If A is exact measurement (e.g. A = 9 or A = π) and Q = Ax, then:
δQ = |A| δx
The general formula (using derivatives) for error propagation (from which all of the other formulas are derived) is: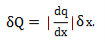
Where Q = Q(x) is any function of x
REGRESSION ANALYSIS
Regression Analysis is a set of statistical processes for estimating the relationships between a dependent variable and one or more independent variables.
Regression analysis is a powerful statistical method that allows you to examine the relationship between two or more variables of interest.
In order to understand regression analysis fully, it’s essential to understand the following terms:
- Dependent Variable: This is the main factor that you’re trying to understand or predict.
- Independent Variables: These are the factors that you hypothesize have an impact on your dependent variable.
Regression analysis is a statistical technique used to describe relationships among variables. The simplest case to examine is one in which a variable Y, referred to as the dependent or target variable, may be related to one variable X, called an independent or explanatory variable, or simply a regressor.
The simplest case to examine is one in which a variable Y, referred to as the dependent or target variable, may be related to one variable X, called an independent or explanatory variable, or simply a regressor. If the relationship between Y and X is believed to be linear, then the equation for a line may be appropriate:
Y=β1+β2X,
Where β1 is an intercept term and β2 is a slope coefficient.
In simplest terms, the purpose of regression is to try to find the best fit line or equation that expresses the relationship between Y and X.
Example: The angle (Θ) between the two lines of regressions x+4y=3 & 3x+y=15 is given by
Answer
m1= slope of line of regression y on x= byx = −1/4
m2= slope of line of regression x on y= 1/ bxy = −3
∴ tanθ = 
= 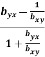 =
= 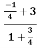
Tanθ =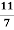
θ = tan-1(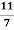 )
)
USES OF REGRESSION
Applications of regression are numerous and occur in almost every field, including engineering, the physical and chemical sciences, economics, management, life and biological sciences, and the social sciences. In fact, regression analysis may be the most widely used statistical technique
Regression models are used for several purposes, including the following:
1. Data description
2. Parameter estimation
3. Prediction and estimation
4. Control
1. Data description
Engineers and scientists frequently use equations to summarize or describe a set of data. Regression analysis is helpful in developing such equations. For example, we may collect a considerable amount of delivery time and delivery volume data, and a regression model would probably be a much more convenient and useful summary of those data than a table or even a graph
2. Parameter estimation
Sometimes parameter estimation problems can be solved by regression methods. For example, chemical engineers use the Michaelis – Menten equation
Y =β1x /( x+β2 ) +ε to describe the relationship between the velocity of reaction y
And concentration x. Now in this model, β1 is the asymptotic velocity of the reaction, that is, the maximum velocity as the concentration gets large. If a sample of observed values of velocity at different concentrations is available, then the engineer can use regression analysis to fit this model to the data, producing an estimate of the maximum velocity.
3. Prediction and estimation
Many applications of regression involve prediction of the response variable. For example, we may wish to predict delivery time for a specified number of cases of soft drinks to be delivered. These predictions may be helpful in planning delivery activities such as routing and scheduling or in evaluating the productivity of delivery operations. The dangers of extrapolation when using a regression model for prediction because of model. However, even when the model form is correct, poor estimates of the model parameters may still cause poor prediction performance.
4. Control
Regression models may be used for control purposes. For example, a chemical engineer could use regression analysis to develop a model relating the tensile strength of paper to the hardwood concentration in the pulp. This equation could then be used to control the strength to suitable values by varying the level of hard-wood concentration. When a regression equation is used for control purposes, it is important that the variables be related in a causal manner.
Regression analysis is helpful statistical method that can be leveraged across an organization to determine the degree to which particular independent variables are influencing dependent variables.
The possible scenarios for conducting regression analysis to yield valuable, actionable business insights are endless.
Some numerical problem related to above topics.
1.Example: The sides of a fence are measured with at tape measure to be 124.2cm, 222.5cm,151.1cm and164.2cm.Each measurement has an uncertainty of 0.07cm.Calculate the measured perimeter including its uncertainty
Solution: P = 124.2cm+222.5cm+151.1cm+164.2cm = 662.0cm
∆P =  = 0.14cm
= 0.14cm
Pm = 662.0cm ±0.1cm
2.Example: The length of metal plate was measured using a vernier callipers of least count 0.01 cm. The measurements made were 3.11 cm, 3.13 cm, 3.14 cm and 3.10 cm. Find absolute error for measurements.
Solution:
Mean length am=43.11+3.13+3.14+3.10=3.12cm
Absolute error for measurements
∣Δa1∣=∣am−a1∣=∣3.12−3.11∣=0.01cm
∣Δa2∣=∣am−a2∣=∣3.12−3.13∣=0.01cm
∣Δa3∣=∣am−a3∣=∣3.12−3.14∣=0.02cm
∣Δa4∣=∣am−a4∣=∣3.12−3.10∣=0.02cm
3.Example: In an experiment, the values of refractive indices of glass were found to be 1.54, 1.53, 1.44, 1.54, 1.56 and 1.45 in successive measurements. Find the Mean absolute error of measurements.
Solution:
Mean=(61.54+1.53+1.44+1.54+1.56+1.45 )/6=1.51
Mean absolute error
(∣1.51−1.54∣+∣1.51−1.53∣+∣1.51−1.44∣+∣1.51−1.54∣+∣1.51−1.56∣+∣1.51−1.45∣)/6
=0.04
4.Example: John measures the size of the metal ball as 3.97 cm but the actual size of it is 4 cm. Calculate the relative error.
Solution:
The measured value of metal ball xo=3.97cm
The true value of ball x = 4 cm
Absolute error=Δx=True value−Measured value=x−xo=0.03
Relative error=xΔx=4(0.03)=0.0075
5.Example: The least count of a stopwatch is 1/5 sec. The time of 20 oscillations of a pendulum is measured to be 25 sec. The maximum percentage error in this measurement is
Solution:
Error % = 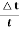 ×100
×100
△t=least count
t=25sec
⇒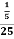 ×100
×100
= = 0.8%
= 0.8%
6.Example: Given that the distribution of student’s height is given by N(62.5, 2.5). What will be the mean and standard deviation if you randomly select 10 women as your sample?
Solution: = μ = 62.5 inches
= μ = 62.5 inches
And
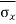 = [σ /
= [σ /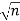 ] = 2.5 /
] = 2.5 /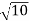 = 0.79 inches
= 0.79 inches
7.Example: The period of oscillation of a simple pendulum is T =2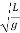 Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution. What is the accuracy in the g?
Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution. What is the accuracy in the g?
Solution:
As
T =2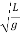 and g = 4π2(L/T2)
and g = 4π2(L/T2)
 x 100 =
x 100 =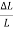 x 100 +2
x 100 +2  x 100)
x 100)
Now L=20.0cm, L=0.1cm, T for 100 oscillation = 90sec , T=1 sec
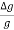 x 100 =
x 100 = 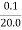 x 100 +2
x 100 +2 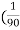 x 100)=0.5 +2.22 =2.72% =3%
x 100)=0.5 +2.22 =2.72% =3%
8. Example: Find the relative error in Z, if Z=A4 B1/3 / CD3/2
Solution: In relative error in Z is
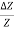 = 4 x
= 4 x 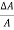 +
+
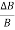 +
+ 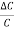 +
+

9. Example: Mean refractive index is given as 1.29, 1.33, 1.34, 1.35, 1.32, 1.36, 1.30, 1.33 find absolute error, Mean Absolute error, Relative error and Percentage error.
Solution:
Mean refractive index is average of eight values i.e.
μmean = (1.29 + 1.33 + 1.34 + 1.35 + 1.32 + 1.36 + 1.30 + 1.33) ÷ 8
μmean =10.62 ÷ 8 = 1.3275 ≈ 1.33
Absolute error are:
Δμ1 = μmean – μ1 = 1.33 – 1.29 = 0.04
Δμ2 = μmean – μ2 = 1.33 – 1.33 = 0.00
Δμ3 = μmean – μ3 = 1.33 – 1.34 = -0.01
Δμ4 = μmean – μ4 = 1.33 – 1.35 = -0.02
Δμ5 = μmean – μ5 = 1.33 – 1.32 = 0.01
Δμ6 = μmean – μ6 = 1.33 – 1.36 = -0.03
Δμ7 = μmean – μ7 = 1.33 – 1.30 = 0.03
Δμ8 = μmean – μ8 = 1.33 – 1.33 = 0.00
Mean Absolute error Δμmean
= (|Δμ1 | + |Δμ2 | + |Δμ3 | + | Δμ4 | + | Δμ5 | + | Δμ6 | + |Δμ7 | + |Δμ8 |) ÷ 8
= ( 0.04 + 0.00 + 0.01 + 0.02 + 0.01 + 0.03 + 0.03 + 0.00) ÷ 8
= 0.14 ÷ 8 = 0.0175 ≈ 0.02
Relative error (δμ) = Δμmean/ μmean = 0.02 ÷ 1.33 = ± 0.015 ≈ 0.02
Percentage error = (Δμmean/ μmean) × 100% = ± 0.015 × 100 = ± 1.5
10. Example: A current of 3.5 ± 0·5 ampere flows through metallic conductor. And a potential difference of 21 ± 1 volt is applied. Find the Resistance of the wire.
Answer: Given V = 21± 1volts, ΔV = 1, I = 3.5 ± 0·5 A and ΔI = 0.5A
Resistance R = V / I = 21± 1 / 3.5 ± 0·5 = 6 ± ΔR
ΔR/R = error in measurement = ΔV/V + ΔI/I = 1/21 + 0.5/3.5 = 0.048 + 0.143 = 0.191 ≈ 0.19
⇒ ΔR = 0.19 × R = 0.19 × 6 = 1.14
∴ Effective resistance R = 6 ± 1.14 Ω
11. Example: A rectangular board is measured with a scale having accuracy of 0.2cm. The length and breadth are measured as 35.4 cm and 18.4 cm respective. Find the relative error and percentage error of the area calculated.
Answer: Given length (l) = 35.4 cm, Δl = 0.2cm
Width  = 18.4cm and Δw = 0.2cm
= 18.4cm and Δw = 0.2cm
Area (A) = l × w = 35.4 × 18.4 = 651.36 cm2
Relative error in Area (δA) = ΔA/A = Δl/l + Δw/w =0.2/35.4 + 0.2/18.4 = 0.006 + 0.011 = 0.017
Percentage error = ΔA/A × 100 = 0.017 × 100 = 1.7%