UNIT 6
Fundamentals of Kinematics and Kinetics of Particles
Motion is one of the most common phenomena we come across in our daily lives. For example, a moving car, a kid running on the road or a fly moving in the air are all said to be in motion. So, in general terms, a body is said to be in motion if it changes its position with respect to a reference point and time. Depending upon the path taken by the particle the motion can be of different types like projectile motion, rectilinear motion, rotational motion, etc. For now, we will only focus on the rectilinear motion which is also known as linear motion.
When we require only one co-ordinate axis along with time to describe the motion of a particle it is said to be in linear motion or rectilinear motion. Some examples of linear motion are a parade of soldiers, a train moving along a straight line, and many more.
Distance and Displacement
So now that we have learned about linear motion we will discuss two terms related to change in position. These are called – ‘Distance’ and ‘Displacement’.
Distance is defined as, The total path length covered during a journey While displacement is defined as, The path length from final position of the particle to the origin O. Consider the following figure:

We have an origin O, measurements to the right of O are taken as a positive while to the left are taken as negative. Suppose a person who starts from origin O reaches point A,
Distance = OA
Displacement = OA
Now he turns and reaches point B,
Distance = OA + AB
Displacement = -OB
As we can see, displacement is negative since it is measured to the left of the origin. From the above example, we can infer that distance is always positive while displacement can either be positive or negative.
Speed and Velocity
These terms are used to describe the rate of change of position. Speed is the rate of change of distance while velocity is the rate of change of displacement. Comparing from above as distance can never be negative so the speed is never negative while velocity can be both positive and negative. In mathematical terms, these are defined as follows:
Speed = Distance Travelled Time Taken
Velocity = (Final position–Initial position) Time Taken
Examples for Rectilinear Motion
Following are the rectilinear motion examples:
- The use of elevators in public places is an example of rectilinear motion.
- Gravitational forces acting on objects resulting in free fall is an example of rectilinear motion.
- Kids sliding down from a slide are a rectilinear motion.
- The motion of planes in the sky is a rectilinear motion.
Curvilinear motion is defined as motion that occurs when a particle travels along a curved path. The curved path can be in two dimensions (in a plane), or in three dimensions. This type of motion is more complex than rectilinear (straight-line) motion.
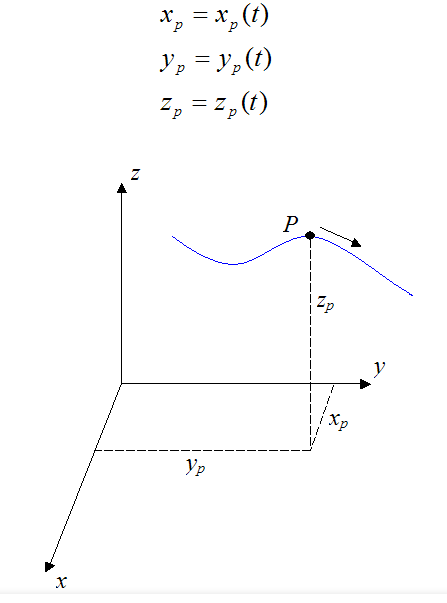
Three-dimensional curvilinear motion describes the most general case of motion for a particle.To find the velocity and acceleration of a particle experiencing curvilinear motion one only needs to know the position of the particle as a function of time.
Let’s say we are given the position of a particle P in three-dimensional Cartesian (x,y,z) coordinates, with respect to time, where
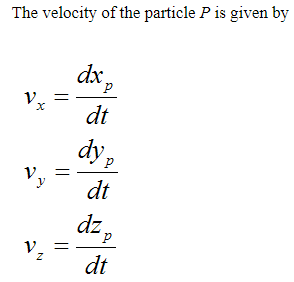
The acceleration of the particle P is given by
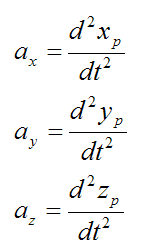
As you can see, if we know the position of a particle as a function of time, it is a fairly simple exercise to find the velocity and acceleration. You simply take the first derivative to find the velocity and the second derivative to find the acceleration.
The magnitude of the velocity of particle P is given by
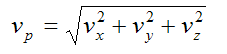
The magnitude of the acceleration of particle P is given by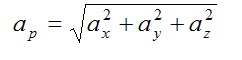
Note that the direction of velocity of the particle P is always tangent to the curve (i.e. the path travelled, denoted by the blue curve in the figure above). But the direction of acceleration is generally not tangent to the curve.
However, the acceleration component tangent to the curve is equal to the time derivative of the magnitude of velocity of the particle P (along the curve). In other words, if vt is the magnitude of the particle velocity (tangent to the curve), the acceleration component of the particle tangent to the curve (at) is simply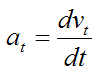
In addition, the acceleration component normal to the curve (an) is given by
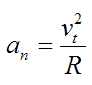
where R is the radius of curvature of the curve at a given point on the curve (xp,yp,zp).
The figure below illustrates the acceleration components at and an at a given point on the curve (xp,yp,zp).

For the specific case where the path of the blue curve is given by y = f(x) (two-dimensional motion), the radius of curvature R is given by
where |x| means the “absolute value” of x. For example, |-2.5| = 2.5, and |3.1| = 3.1.
However, it is usually not necessary to know the radius of curvature R along a curve. But nonetheless, it is informative to understand it on the basis of its relationship to the normal acceleration (an).
A rigid body is an idealization of a solid body where the deformations occurring on the body are neglected. In other words, the distance between any two given points of a rigid body remains a constant regardless of the external force acting upon it.
The concept of rigid body and Rigid body dynamics was developed to solve a range of problems that could not be explained with classical physics. Motions such as rotation of a fan, a potter’s wheel, a top, etc cannot be adequately explained with a point mass. In real life, in the case of bodies such as wheels and steel rods, deformation or bending is considered to be negligible, and we treat them as rigid.
Rigid Body Dynamics:
The question is, what kind of motion can a rigid body have? This new outlook meant that there now could be two different types of rigid body motion. We could explore and understand more kinds of problems and in doing so develop a deeper understanding of the world around us. Rigid Body Dynamics laid the foundation to what has come after, Quantum Mechanics. The two types of motion a rigid body can undergo are;
- Translational Motion
- Rotational Motion
Configuration Space for a Rigid Body:
A macroscopic body is made up of a very large number of atoms. Describing the motion of such a system without some simplifications is clearly impossible. Many objects of interest, however, are very well approximated by the assumption that the distances between the atoms in the body are fixed. This constitutes a set of holonomic constraints, but not independent ones, as we have here 12n(n−1) constraints on 3n coordinates.
Rather than trying to solve the constraints, we can understand what are the generalized coordinates by recognizing that the possible motions which leave the interparticle lengths fixed are combinations of translations of the body as a whole, r⃗ α→r⃗ α+C⃗ and rotations of the body about some fixed, or “marked”, point.
We will need to discuss how to represent the latter part of the configuration, (including what a rotation is), and how to re-express the kinetic and potential energies in terms of this configuration space and its velocities.
The first part of the configuration, describing the translation, can be specified by giving the coordinates of the marked point fixed in the body, R~(t). Often, but not always, we will choose this marked point to be the center of mass R⃗ (t) of the body.
In order to discuss other points that are part of the body, we will use an orthonormal coordinate system fixed in the body, known as the body coordinates, with the origin at the fixed point R~.
The constraints mean that the position of each particle of the body has fixed coordinates in terms of this coordinate system. Thus, the dynamical configuration of the body is completely specified by giving the orientation of these coordinate axes in addition to R~. This orientation needs to be described relative to a fixed inertial coordinate system, or inertial coordinates, with an orthonormal basis ei.
Stay tuned with BYJU’S to learn more about Rigid Body Dynamics, Translational Motion and Rotational Motion, and much more with interesting video lectures.
Newton’s First Law of Motion

The first law of motion implies that things cannot start, stop, or change direction all by themselves. It requires some force from the outside to cause such a change. This property of massive bodies to resist changes in their state of motion is called inertia. Newton’s first law is also known as the law of inertia.
Newton’s 1st law states that a body at rest or uniform motion will continue to be at rest or uniform motion until and unless a net external force acts on it.
Newton’s Second Law of Motion
The second law of motion describes what happens to the massive body when acted upon by an external force. The 2nd law of motion states that the force acting on the body is equal to the product of its mass and acceleration.
Newton’s 2nd law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
Newton’s second law describes precisely how much an object will accelerate for a given net force.
Mathematically, we express the second law of motion as follows:
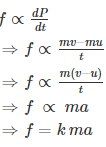
In the equation, k is the constant of proportionality, and it is equal to 1 when the values are taken in SI unit. Hence, the final expression will be,
F=ma
Newton’s Third Law of Motion

The third law of motion describes what happens to the body when it exerts a force on another body.
The Newton’s 3rd law states that for every action there is an equal and opposite reaction.
When two bodies interact, they apply force on each other that are equal in magnitude and opposite in direction. To understand Newton’s third law with the help of an example, let us consider a book resting on a table. The book applies a downward force equal to its weight on the table. According to the third law of motion, the table applies an equal and opposite force on the book. This force occurs because the book slightly deforms the table; as a result, the table pushes back on the book like a coiled spring.
The kinetic energy of an object is the energy associated with the object which is under motion. It is defined as “the energy required by a body to accelerate from rest to stated velocity.” It is a vector quantity.
Mathematically expressed as-
K.E=1/2mv2
Where,
m is the mass of the object measured in kg.
v is the velocity of the object measured in m/s
Kinetic Energy unit
The SI Unit of Kinetic Energy is Joules.
Momentum
The momentum of an object is the virtue of its mass. It is defined as the product of mass and velocity. It is a vector quantity.
The momentum of a moving object can be mathematically expressed as –
p=mv
Where,
- p is the momentum.
- m is the mass of the object measure using kg.
- v is the velocity of object measure using m/s.
Momentum unit
The SI Unit of Momentum is kg.m/s
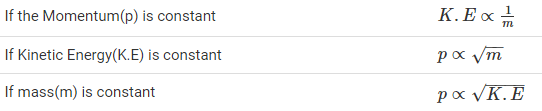
Relation between Momentum and Kinetic Energy
Kinetic energy and momentum of a moving body can be mathematically related as follows-
Consider the formula of kinetic energy-
K.E=1/2mv2
Multiply and divide R.H.S by m
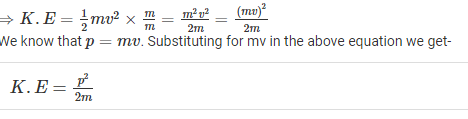
The above equation gives the relation between Kinetic energy and momentum of the object which is under motion.