UNIT 5
Centroid and Centre of Gravity
The Centroid is the average position of all the points of an object. When we cut a plane shape from a piece of card it balances perfectly on its centroid.
Center of Gravity
The Center of Gravity is the same as the centroid when the density is the same throughout. Center of gravity centre of mass and centroid are all the same for simple solids. They are often marked by a cross or dot and sometimes the letters CG or just G

For a torus the centroid is at the very center (even though there is no part of the torus there!)
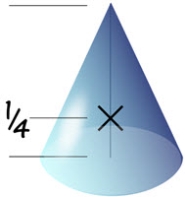
For a right solid cone the centroid is on the center line and ¼ of the way from the base

The center of gravity of a car can be very hard to figure out, as there is lots of empty space and materials of different density (such as the engine vs the seats).
1. Definition of Gravity and Centroid
Centre of gravity is the point where the total weight of the body acts while centroid is the geometric centre of the object. Centre of gravity or centre of mass is the point where the whole mass of the body is concentrated. This is where the gravitational force (weight) of the body acts for any orientation of the body. Centroid is the centre of gravity for objects of uniform density.
2. Calculation of Gravity and Centroid
Calculating centre of gravity is not a simple procedure because the mass (and weight) may not be uniformly distributed throughout the object. Centre of gravity can be calculated from cg * W = S x dw where x is the distance from a reference line, dw is an increment of weight, and W is the total weight of the object. Centroid can be found with methods such as the plumb line method discussed above.
Centre of Gravity vs. Centroid: Comparison Chart
Centre of Gravity | Centroid |
Centre of mass of a geometric object with any density | Centre of mass of a geometric object of uniform density |
Point where weight of a body or system may be considered to act | Geometrical centre |
Denoted by g | Denoted by c |
Summary of Gravity and Centroid
- The gravitational forces of the elementary parts of which the body is composed can be replaced with the action of a resultant force with intensity as large as the weight of the body directed at the centre of gravity of the body.
- The centre of gravity is located in the intersection of the gravitational lines, and in the correct geometric bodies is determined geometrically. This is true if the density of the substance throughout the body is the same, i.e. that the body is homogeneous. In that case the centre of gravity is equivalent with the centroid of the body
- Centroid is the average position of all the points of an object. It is the point at which a cutout of the shape could be perfectly balanced
Centre of gravity, in physics, an imaginary point in a body of matter where, for convenience in certain calculations, the total weight of the body may be thought to be concentrated. The concept is sometimes useful in designing static structures (e.g., buildings and bridges) or in predicting the behaviour of a moving body when it is acted on by gravity.
Centre of gravity
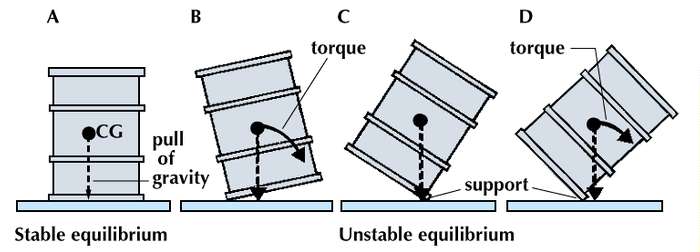
When a drum is stood on end, its centre of gravity (CG) is firmly supported, and the drum is in stable equilibrium (A). If the drum is tilted slightly to either side (B), the pull of gravity on this centre creates a torque, or turning force, around the new point of support and pulls the drum back to the stable position. A drum balanced on its rim (C) is in unstable equilibrium. Even a tiny displacement (D) will create a torque that will turn the drum farther from the unstable position.
In a uniform gravitational field the centre of gravity is identical to the centre of mass, a term preferred by physicists. The two do not always coincide, however. For example, the Moon’s centre of mass is very close to its geometric centre (it is not exact because the Moon is not a perfect uniform sphere), but its centre of gravity is slightly displaced toward Earth because of the stronger gravitational force on the Moon’s near side.
The location of a body’s centre of gravity may coincide with the geometric centre of the body, especially in a symmetrically shaped object composed of homogeneous material. An asymmetrical object composed of a variety of materials with different masses, however, is likely to have a centre of gravity located at some distance from its geometric centre. In some cases, such as hollow bodies or irregularly shaped objects, the centre of gravity (or centre of mass) may occur in space at a point external to the physical material—e.g., in the centre of a tennis ball or between the legs of a chair.

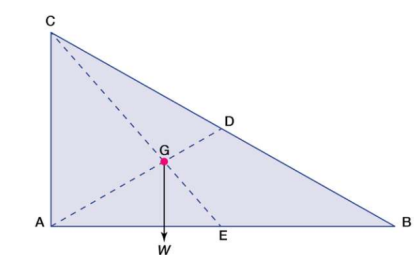
Published tables and handbooks list the centres of gravity for most common geometric shapes. For a triangular metal plate such as that depicted in the figure, the calculation would involve a summation of the moments of the weights of all the particles that make up the metal plate about point A. By equating this sum to the plate’s weight W, multiplied by the unknown distance from the centre of gravity G to AC, the position of G relative to AC can be determined. The summation of the moments can be obtained easily and precisely by means of integral calculus.
Centre of gravity
Centre of gravity. The red dot is the centre of gravity G.
The centre of gravity of anybody can also be determined by a simple physical procedure. For example, for the plate in the figure, the point G can be located by suspending the plate by a cord attached at point A and then by a cord attached at C. When the plate is suspended from A, the line AD is vertical; when it is suspended from C, the line CE is vertical. The centre of gravity is at the intersection of AD and CE. When an object is suspended from any single point, its centre of gravity lies directly beneath that point.
Taking the simple case first, we aim to find the centroid for the area defined by a function f(x), and the vertical lines x = a and x = b as indicated in the following figure.
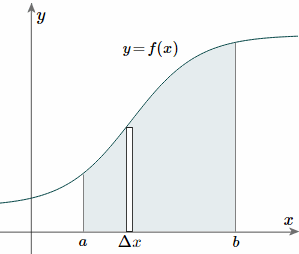
To find the centroid, we use the same basic idea that we were using for the straight-sided case above. The "typical" rectangle indicated is x units from the y-axis, and it has width Δx (which becomes dx when we integrate) and height y = f(x)
Generalizing from the above rectangular areas case, we multiply these 3 values x, f(x) and Δx, which will give us the area of each thin rectangle times its distance from the x-axis), then add them. If we do this for infinitesimally small strips, we get the x-coordinates of the centroid using the total moments in the x-direction, given by:
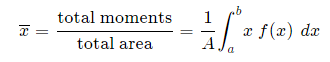
And, considering the moments in the y-direction about the x-axis and re-expressing the function in terms of y, we have:
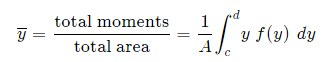
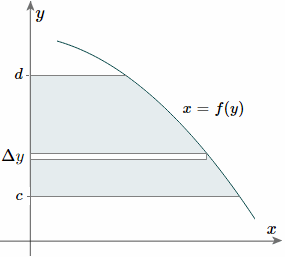
Notice this time the integration is with respect to y, and the distance of the "typical" rectangle from the x-axis is y units. Also note the lower and upper limits of the integral are c and d, which are on the y-axis.
Of course, there may be rectangular portions we need to consider separately. (I've used a different curve for the y case for simplification.)
Alternate method: Depending on the function, it may be easier to use the following alternative formula for the y-coordinate, which is derived from considering moments in the x-direction (Note the "dx" in the integral, and the upper and lower limits are along the x-axis for this alternate method).
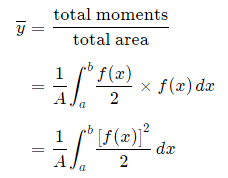
This is true since for our thin strip (width dx) the centroid will be half the distance from the top to the bottom of the strip. Another advantage of this second formula is there is no need to re-express the function in terms of y.
Centroids for Areas Bounded by 2 Curves
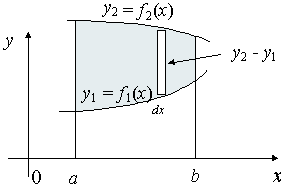
We extend the simple case given above. The "typical" rectangle indicated has width Δx and height y2 − y1, so the total moments in the x-direction over the total area is given by:
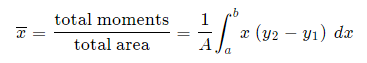
For the y coordinate, we have 2 different ways we can go about it.
Method 1: We take moments about the y-axis and so we'll need to re-express the expressions x2 and x1 as functions of y.
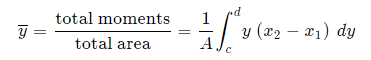
Method 2: We can also keep everything in terms of x by extending the "Alternate Method" given above:
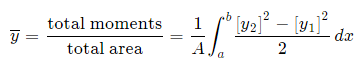
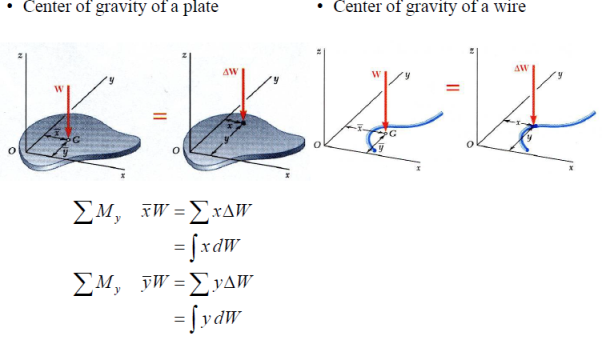

First Moments of Areas and Lines
•An area is symmetric with respect to an axis BB’ if for every point P there exists a point P’ such that PP’ is perpendicular to BB’ and is divided into two equal parts by BB’.
•The first moment of an area with respect to a line of symmetry is zero.
•If an area possesses a line of symmetry, its centroid lies on that axis
•If an area possesses two lines of symmetry, its centroid lies at their intersection.
•An area is symmetric with respect to a center O if for every element dA at (x,y) there exists an area dA’ of equal area at (-x,-y).
•The centroid of the area coincides with the center of symmetry.

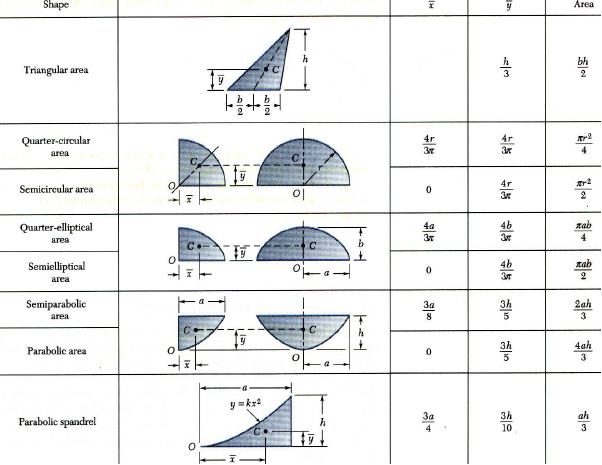
Centroids of Common Shapes of Areas: