Unit - 2
Available energy
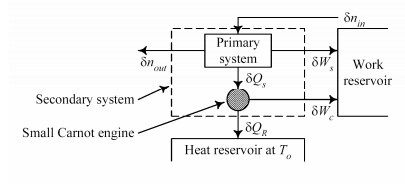
Consider a fully reversible process with no dissipative effects – that is all work is transferred without loss and all heat is transferred using an ideal Carnot process to generate additional work.
The resulting maximum work in Secondary system given by
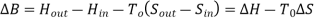
ΔB= change in availability
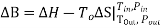
Clearly, the availability B is a state function in the strictest mathematical sense so the maximum (or minimum) work associated with any steady state process is also independent of the path. Availability: • Yields the maximum work producing potential or the minimum work requirement of a process •Allows evaluation and quantitative comparison of options in a sustainability context
Before deriving a general mathematical definition that relates Exergy to other state variables and state functions (i.e., “properties”), the following simple example of transforming heat to work is used to illustrate the concept of Exergy in its simplest form.
The Kelvin-Planck formulation of the 2nd Law of Thermodynamics states that network cannot be produced from a thermodynamically cyclic process if there is interaction (i.e., heat transfer) with only one thermal reservoir. The simplistic understanding of this is that heat cannot be converted to work on a 1:1 basis (i.e., with 100% efficiency), see Figure 1.a. In fact, the mathematical representation of Kelvin-Planck (Wcycle 0) indicates that no work can be produced, and equality (Wcycle 0) only applies to the reversible case.
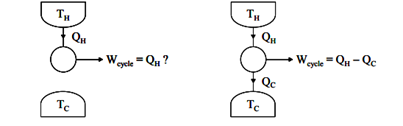
If, on the other hand, the thermodynamically cyclic process interacts with two thermal reservoirs (extracts heat QH from a reservoir with temperature TH and delivers heat QC to a reservoir with temperature TC TH), see Figure 1.b, then some work can be delivered by the system, ranging from zero to an upper bound given by the 2nd Law of Thermodynamics as shown below. For a cyclic process, the 1st Law of Thermodynamics reduces to:
∆Ucycle = Qcycle –Wcycle= 0
Wcycle= Qcycle=QH-QC ……3
Notice that the sign convention of Mechanical Engineering Thermodynamics (heat is positive if received by the system from the surroundings, and work is positive if developed by the system and applied to the surroundings) is not used here; all entities are regarded to be positive, and the arrows in Figures 1.a and 1.b indicate the direction of heat and work between the system (undergoing a cyclic process) and the surroundings. The work that can be developed from an arrangement as the one in Figure 1.b is then constrained to be in the following range:
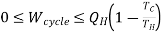 ……4
……4
In Equation 4, one recognizes the maximum thermal efficiency to be that of the Carnot cycle, which is a reversible cyclic process with 2 adiabatic and 2 isothermal stages:
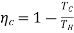 …….5
…….5
Rather than focusing on a cyclic process operating between two thermal reservoirs, consider an amount of heat Q at a temperature T. The amount of Exergy that this heat represents is stated by words in Section 1 to be the maximum amount of work (i.e., Ideal Work) that can be developed if equilibrium is established with the surroundings and only reversible processes are involved. A common definition of the surroundings is (despite variations in climate across the world) a large thermal reservoir with a fixed temperature T 0 = 25ºC (or ≈ 298 K) and a fixed pressure 0 p = 1 atm (or ≈ 1 bar).
Using Equation 4 and an analogy to the case in Figure 1.b, the surroundings act as the cold reservoir, while heat Q at a temperature T acts as the hot reservoir. The Exergy content of heat Q is then the maximum amount of work that can be extracted from this arrangement:
 ……...6
……...6
Equation 6 illustrates one important fact regarding the Energy Quality of heat. For a given amount of heat Q, the amount of work that can be produced (and thus its Exergy or Energy Quality) increases with temperature. Thus, temperature is a quality parameter for heat.
A common graphical illustration of the quality (or Exergy) of heat is shown in Figure 2. The illustration is made in a Ts-diagram, since heat for internally reversible processes can be found from the following integral:
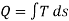
Heat (as a form of energy) can be divided into one part that can produce work (its Exergy), and one part that cannot be used to produce work, which is commonly referred to as Anergy. For heat Q at temperature T, the following decomposition can be made with reference to the ambient temperature T0:
Energy =Exergy+ Anergy
Flow Processes:
1. Flow process is one in which there is energy as well as mass transfer across the boundary of the system. Following are the flow processes.
(i) from inlet of compressor to its outlet in a refrigeration system
(ii) Through a nozzle
(iii) flow across a turbine.
2. Flow process takes place in an open system.
3. Steady flow system in which properties do not change with respect to time.
4. Steady flow energy equation is a heat balance for the system.
5. Work done in an open system is n times the work done in a closed system.
6. All flow systems are OPEN systems since energy and work cross their boundaries.
7. When properties are constant with respect to time it is called a steady flow system. All the experimental data is recorded under steady flow conditions.
8. When properties vary with respect to time it is called a non-steady flow system. Nothing useful can be found under unsteady flow conditions.
9. Firstly, work done in a poly-tropic process in open system is n times in a closed system
10. Secondly work Done in a poly-tropic compression (closed system) =∫p dv =(p2v2–p1v1)/(n-1)
11. Thirdly work Done in a poly-tropic compression (Open system)
An irreversible process is one in which heat is transferred through a finite temperature
Example: 1. relative motion with friction
2. Combustion
3. Diffusion
An irreversible process is usually represented by a dotted line joining the end states to indicate that the intermediate.
Two types of irreversibility.
External irreversibility: These are associated with dissipating effects outside the working fluid.
Internal irreversibility: these are associated with dissipating effects within the working fluid.
In open and closed systems, energy can cross the boundary in the form of heat q and work W. If the energy exchange is because of temperature difference between a system and its surroundings, this energy exchange appears as heat otherwise it appears as work. When a force acts on a system through a distance, then energy is transferred as work. The heat and work interactions change the internal energy of a closed system ΔU, which is estimated by
∆U=q+W
According to the modern energy sign convention recommended by the International Union of Pure and Applied Chemistry, heat and work are considered positive for their transfers into the system from their surroundings. Heat and work are negative when they are transferred out of the system to the surroundings. Total internal energy is an extensive property as its value depends on the quantity of material in a system. Finite exchanges of energy between a system and its surroundings obey the energy balance
∆ (Energy of the system) +∆ (Energy of the surroundings) = 0
It shows the mass and energy interactions between a system and its surroundings. As the energy is conserved, the net rate of change of energy within the system is equal to the net rate of energy exchanged between the system and its surroundings at steady state. Streams in various numbers may flow into and out of Energy Balances the system. These streams may have energy associated with them in the forms of internal, kinetic, and potential energies. All these forms of energy contribute to the energy change of the system.
The second law states that, due to the increase in entropy, heat cannot be converted to work without creating some waste heat. There due important efficiency equations with respect to this concept:

The temperatures here should be in Kelvin K = ºC + 273.15 or Rankin = 460 + ºF.
2. Second Law Efficiency Second Law efficiency is a measure of how much of the theoretical maximum (Carnot) you achieve, or in other words, a comparison of the system’s thermal efficiency to the maximum possible efficiency. The Second Law efficiency will always be between the Carnot and First Law efficiencies
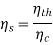
Some thermodynamic properties can be measured directly, but many others cannot. Therefore, it is necessary to develop some relations between these two groups so that the properties that cannot be measured directly can be evaluated. The derivations are based on the fact that properties are point functions, and the state of a simple, compressible system is completely specified by any two independent, intensive properties.
Some Mathematical Preliminaries
Thermodynamic properties are continuous point functions and have exact differentials. A property of a single component system may be written as general mathematical function z = z (x, y). For instance, this function may be the pressure P = P (T, v). The total differential of z is written as.
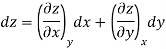
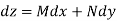
where
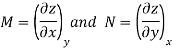
Taking the partial derivative of M with respect to y and of N with respect to x yields.
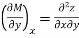 and
and 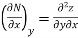
Since properties are continuous point functions and have exact differentials, the following is true

The equations that relate the partial derivatives of properties P, v, T, and s of a simple compressible substance to each other are called the Maxwell relations. They are obtained from the four Gibbs equations. The first two of the Gibbs equations are those resulting from the internal energy u and the enthalpy h.
du= T ds- Pdv
dh= T ds + v dP
The second two Gibbs equations result from the definitions of the Helmholtz function a and the Gibbs function g defined as
a= u - Ts
da = du - T ds - sdT
da = sdT - Pdv
g = h - Ts
dg = dh – T – ds - sdT
dg = sdT + v dP
Setting the second mixed partial derivatives equal for these four functions yields the Maxwell relations.


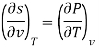
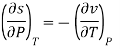
Now we develop two more important relations for partial derivatives—the reciprocity and the cyclic relations. Consider the function z = z (x, y) expressed as x = x (y, z). The total differential of x is
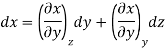
Now combine the expressions for dx and dz.
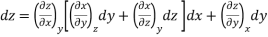
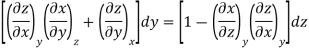
Since y and z are independent of each other, the terms in each bracket must be zero. Thus, we obtain the reciprocity relation that shows that the inverse of a partial derivative is equal to its reciprocal.
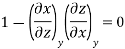
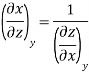
The second relation is called the cyclic relation
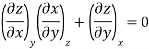
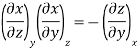
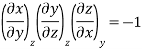
A substance can exist in three states; solid, liquid and gas. Out of these three, only two states can generally coexist in equilibrium. Whenever there is a change of state, either solid changes into liquid or liquid changes into vapour, the temperature remains constant during the change of state. This temperature, although depends upon pressure, is characteristic of each substance. When the change is from solid to liquid state, the characteristic temperature is called the melting point of the solid and when it is from liquid to vapour state, the temperature is called the boiling point of the liquid. The melting point or boiling point have got a specific value at a specific pressure and vice versa. It is possible to obtain a relation showing how the melting and boiling points vary with pressure by applying the second law of thermodynamics.
The idea is to run a Carnot engine between temperatures and T-dT for a two-phase medium and to let it undergo a change in phase. We can then derive an important relation known as the Clausius-Clapeyron equation, which gives the slope of the vapor pressure curve. We could then measure the vapor pressure curve for various substances and compare the measured slope to the Clausius-Clapeyron equation.
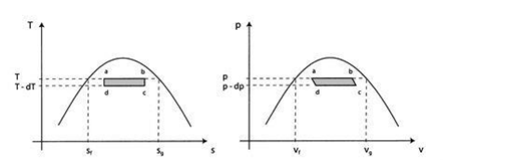
Consider the infinitesimal Carnot cycle abcd shown in figure (a) (b). Heat is absorbed between states a and b. To vaporize an arbitrary amount of mass m, the amount of heat.
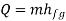
must be supplied to the system. From the 1st and 2nd laws of thermodynamics the thermal efficiency for a Carnot cycle can be written as

Hence, for the infinitesimal cycle considered above

The work along bc and da nearly cancel such that the network is the difference between the work along and ab and cd and dW can be viewed as the area enclosed by the rectangle abcd.
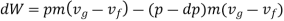

Substituting Equations (1) and (3) into (2) we obtain
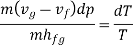
Rearranging terms yields the Clausius-Clapeyron equation, which defines the slope of the vapour pressure curve:
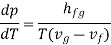
The beauty is that we have found a general relation between experimentally measurable quantities from first principles (1st and 2nd laws of thermodynamics). The Clapeyron’s latent heat equation holds for both the changes of state, i.e., from liquid to vapour and solid to liquid. In the later case hfg will represent the latent of fusion
The relations between the thermodynamic properties of a system are traced to the combined form of the first and second laws. The actual derivation may be done in a variety of ways. The simplest and most methodical procedure is to make the TdS equations and the energy equations the starting point. The three Tds equations are obtained by expressing the specific entropy as a function of the pairs of variables, (T, V), (T, P) and (P, V).
Taking entropy S as a function of volume V and temperature T i.e. S= f (V, T)
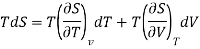
The 1st term of the right side of this equation is expressed in terms of CV, the specific heat at constant volume i.e., the volume becomes constant, hence change in volume dV = 0, now
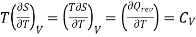
Eq. (1) reduces to
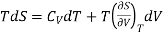
According to Maxwell’s relation

Hence, Eq. (3) reduces to
 …4
…4
This is known as 1st TdS equation.
Taking entropy S as a function of Pressure P and Temperature T. i.e., S= f (P, T)
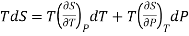 ….5
….5
The 1st term of the right side of this equation is expressed in terms of CP, the specific heat at constant pressure i.e., the volume becomes constant, hence change in pressure dP = 0, Now
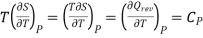
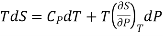 …7
…7
According to Maxwell’s thermodynamic relation
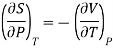
 ….8
….8
This is 2nd TdS equation. (iii) Taking entropy S as a function of Pressure P and volume V. i.e., S= f (P, V)
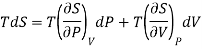
Now,
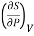 =
=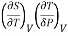

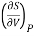 =
=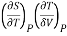

Putting in eq.


This is 3rd TdS equation.
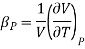
And in terms of isothermal compressibility
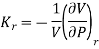
From Eq. (11) and Eq. (12), the ratio

The TdS equation may be written as
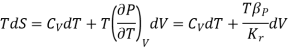
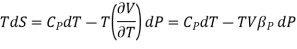
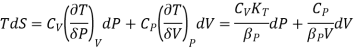
The isothermal compressibility is defined by the fractional differential change in volume due to a change in pressure.
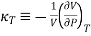
The negative sign is important in order to keep the value of kT positive, since an increase in pressure will lead to a decrease in volume. The 1/V term is needed to make the property intensive so that it can be tabulated in a useful manner.
There is a pressure drop associated with flow through a restriction like valves, capillary tube, porous plug etc.
• The enthalpy of the fluid remains a constant.
• The temperature of a fluid may increase, decrease, or remain constant during a throttling process.
• The behaviour of fluids in such flows is described by the Joule-Thomson coefficient. The Joule-Thomson coefficient is defined as:
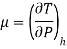
The Joule-Thomson coefficient is a measure of the change in temperature with pressure during a constant-enthalpy process.

Some h= constant lines on the T-P diagram pass through a point of zero slope or zero Joule-Thomson coefficient
•The line that passes through these points is called the inversion line, and the temperature at a point where a constant-enthalpy line intersects the inversion line is called the inversion temperature.
• The slopes of the h=constant lines are negative (μ0) to the left of the inversion line.
References:
1. Engineering Thermodynamics by P. K. Nag, Publisher: TMH
2. Engineering Thermodynamics by P. Chattopadhyay, OXFORD
3. Fundamentals of Thermodynamics by Sonntag, Borgnakke, Van Wylen, John Wiley & Sons
4. Thermodynamics An Engineering Approach by Yunus A. Cingel and Michale A. Boles, TMH
5. Engineering Thermodynamics by M. Achyuthan, PHI