Unit - 1
Review of First and Second laws
This law may be stated as follows:
(a) 'The heat and mechanical work are mutually convertible". According to this law, when a closed system undergoes a thermodynamic cycle, the net heat transfer is equal to the net work transfer. In other words, the cyclic integral of heat transfers is equal to the cyclic integral of work transfers.
Mathematically,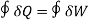 
where symbol f stands for cyclic integral (integral around a complete cycle), and ∂Q and ∂W represent infinitesimal elements of heat and work transfers respectively. It may be noted that ∂Q and ∂W are expressed in same units.
(b) The energy can neither be created nor destroyed though it can be transformed from one form to another. According to this law, when a system undergoes a change of State (or a thermodynamic process), then both heat transfer and work transfer takes place. The net energy transfer is stored within the system and is known as stored energy or total energy of the system. Mathematically
∂Q-∂W=dE
The symbol ∂ is used for a quantity which is inexact differential and symbol d is used for a quantity which is an exact differential. The quantity E is an extensive property and represents the total energy of the system at a particular State.
On integrating the above expression for a change of state from 1to 2, we have
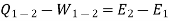… (Q, W and E are in same units)
For a unit mass, this expression is written as
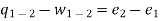
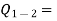Heat transferred to the system during the process from state 1 to state 2,
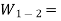Work done by the system on the surroundings during the process
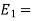Total energy of the system at the state 1
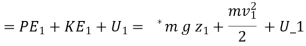
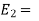Total energy of the system at the state 2
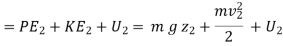
Thus, the above expression may be written as
… (i)
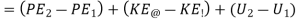… (ii)
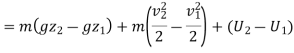
For unit mass, this expression is written as
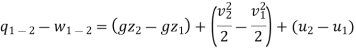
1. When there is no change in potential energy of the system (i.e., when the height of the system from the datum level is same), then PE1=PE2. Thus, the above equation (ii) is written as
Q1-2 - W1 _2 (KE2 - KE1) + (U 2 - U1) - - - (iii)
2. When there is no change of PE and also there is no flow of the mass into or out of the system, then PEI PE2 and KE1. Thus, the above equation (ü) is written as
Q12 —W12 = U2 —U1 = dU ... (iv)
In other words, in a closed or non-flow thermodynamic system,
PE=0 and KE=0
Thus, the equation (iv) is known as non-flow energy equation.
3. For an isolated system for which Q1 _2 = W12=0, the above equation (i) becomes
E2 = E1
This shows that the first law of thermodynamics is the law of conservation of energy.
Limitations of First Law of Thermodynamics
We have already discussed that according to first law of thermodynamics that - When a closed system undergoes a thermodynamic cycle, the net heat transfer is equal to the net work transfer. This statement does-not specify the direction of flow of heat and work (i.e., whether the heat flows from a hot body to a cold body or from a cold body to a hot body). It also does not give any condition under which these transfers take place.
2 The heat energy and mechanical work are mutual!) convertible. Though the mechanical work can be fully converted into heat energy, but only a part of heat energy can be converted into mechanical work. This means that the heat energy and mechanical work are not fully mutually convertible. In other words, there is a limitation on the conversion of one form of energy into another form.
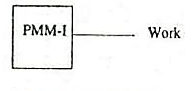
A machine which violates the first law of thermodynamics (i.e., energy can neither be created nor destroyed, but can be transformed from one form to another) is known as perpetual motion machine of the first kind (briefly written as PMM-I). It is defined as which produces work energy without consuming a machine of the first kind. equivalent of energy from other source. Such a machine, as shown in Fig. 1. 10, is impossible to obtain in actual practice, because no machine can produce energy of its own without consuming any other form of energy.
Second laws
The second law of thermodynamics may be defined in many ways, but the two common statements according to Kelvin - Planck and Clausius areas follows.
According to Kelvin-Planck 'It is impossible to Construct an engine working on a cyclic process, whose sole purpose is to convert heat energy from a single thermal reservoir into an equivalent amount of work'. In other words, no actual heat engine, working on a cyclic process, can convert whole of the heat supplied to it, into mechanical work. It means that there is a degradation of energy in the process of producing mechanical work from the heat supplied. Thus, the Kelvin - Planck statement it of the second law of thermodynamics, is sometimes known as law of degradation of energy
100 percent efficient machine which is impossible to obtain in actual practice, because no machine can convert whole of the heat energy supplied to it, into its equivalent amount of work.
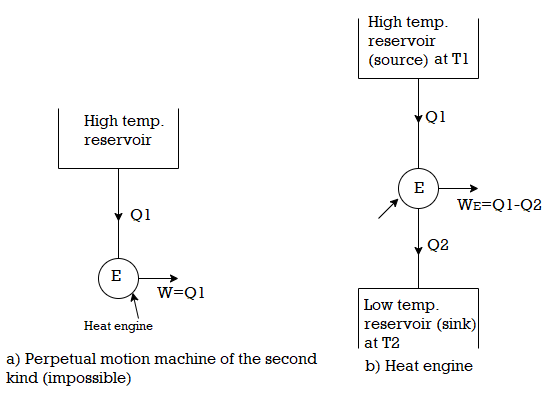
Thus, for the satisfactory operation of a heat engine which is a device used for converting heat energy into mechanical work, there should be at-least two reservoirs of heat, one at a higher temperature and the other at a lower temperature, as shown in Fig. In this case, consider that heat energy (Q 1) from the high temperature reservoir (or Source) at temperature T1 is supplied to the engine. A part of this heat energy is rejected to the low temperature reservoir (or sink) at temperature 1'2. If Q2 is the heat rejected to the sink, then the remaining heat (i.e., Q1 - Q2) is converted into mechanical work. The ratio of the maximum mechanical work obtained to the total heat supplied to the engine is known as maximum thermal efficiency (ii) of the engine. Mathematically
For a reversible engine, 
Steady flow processes:
rates of flow of mass, energy are constant across the system boundary – e.g., Turbines, compressors, heat exchangers etc
Energy analysis of steady flow systems: Several engineering devices can be approximated to operate as steady flow devices: turbine, compressors, nozzles etc.
• During a steady-flow process, no intensive or extensive properties within the control volume change with time.
• The boundary work is zero for steady-flow systems (since VCV =constant).
• The total mass or energy entering the control volume must be equal to the total mass or energy leaving it
Properties of steady flow processes
Unsteady flow processes:
rates of mass, energy are not constant across the system boundary – e.g., Charging and discharging process (tanks, pipelines etc.)
In other words, the integral remains the same no matter what the path is. It can be simply written as S 2-S1. The value depends only on the end states and not on the path followed. So, it is a state function or a property. Like energy entropy (s) is also an extensive property. It will have the units of J/K. Similar to energy where we converted it into specific property, specific entropy (lower case s) will have units of J/kg K (same as specific heat)
∫2 δQ /T= S 2-S 1 or 1 ∫2 δq /T= s 2-s 1 ⏐ δq /T= δs or δq = T δs
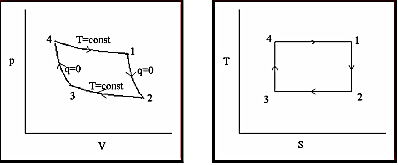
Figure (i) Integrals under P-V plane give work interaction (ii) Integrals under T-S plane give heat interactions
A system is closed if mass does not cross the system boundary during the period of time covered by energy balance. Energy balance for a closed system written between two instants of time is
∆U + ∆Ek + ∆Ep = Q − W
∆U is change internal energy, ∆Ek is change in kinetic energy and ∆Ep is change in potential energy, Q is heat transferred to the system and W is work done by the system. We take heat lost to surroundings as –ve and heat transferred to the system as +ve.
If the system is adiabatic, there is neither gain by the system not heat loss and Q is zero. If there are no moving parts, then W is zero.
Energy Balances on Open Systems
A system is open if mass crosses the system boundary. For such a system, work must be done on the fluid mass to push it into the system and work is done by the fluid mass exiting the system. These two constitute the flow work and should be included in the energy balance. Work could also be done by the fluid mass on moving parts of the system (example: steam driving a turbine). This is called shaft work.
The net rate of work done by an open system on its surroundings includes the works discussed above:
W= Ws+ Wfl
Ws is the shaft work and Wn is the flow work.
To understand shaft work, consider a single-inlet and single-outlet system into which fluid enters at Pin (N/m2) at a volumetric flow rate of Vin • (m3 /s) and leaves the unit at Pout (N/m2) at a volumetric flow rate of Vout • (m3 /s).
Work required to push the mass in = Pin Vin
• Work done by the fluid exiting the system = Pout Vout
• The net rate of work done by the system = Pin Vin - Pout Vout
• The energy balance takes the following form:
∆H+ ∆Ek+ ∆Ep= Q - Ws
∆ H is rate of change of enthalpy, a term defined below. ∆Ek is rate of change of kinetic energy and ∆Ep is rate of change of potential energy, • Q is rate at which energy is transferred to the system and Ws • is the rate at which work is done by the fluid on the system.
References:
1. Engineering Thermodynamics by P. K. Nag, Publisher: TMH
2. Engineering Thermodynamics by P. Chattopadhyay, OXFORD
3. Fundamentals of Thermodynamics by Sonntag, Borgnakke, Van Wylen, John Wiley & Sons
4. Thermodynamics An Engineering Approach by Yunus A. Cingel and Michale A. Boles, TMH
5. Engineering Thermodynamics by M. Achyuthan, PHI
