Unit – 5
Torsion
A member which subjected to couple which produce rotation about its longitudinal axis is known as Twisting moment or Torsion.
Due to Torque applied on shaft, the shaft produces shear stress and shear strain in the material.
In practice, torque is produced in shaft of motors or power equipments e.g. Fans, axles of vehicles, pumps, etc.
Shaft are circular in section only, hollow shaft is preferable for design.
Examples:
1. A metal bar 15mm diameter subjected to pull of 40KN elongated by 0.5 mm over a gauge length of 500 mm. In a torsion test on the same material, maximum shear stress of 45Mpa was measured on a bar of 50mm diameter and an angle of twist over a length of 300 mm was measured 0.4 degree. Determine Poisson’s ratio for the material.
Ans:
Given:
Tensile test: D = 15mm P = 40KN
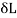 = 0.5 mm L = 500 mm
= 0.5 mm L = 500 mm
 = 45Mpa D = 50 mm
= 45Mpa D = 50 mm
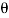 = 0.4
= 0.4 L = 300mm
L = 300mm
To find: 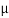
(i) Modulus of elasticity from tension test.
E =  =
= 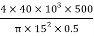 = 226.35
= 226.35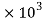 Mpa
Mpa
(ii) Shear modulus from torsion test:
G = 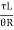 = 77.35
= 77.35 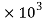 Mpa
Mpa
(iii) Possion ratio
E = 2G (1+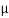 )
)
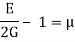
 = 1.463-1 = 0.463
= 1.463-1 = 0.463
2. A hollow circular of 200mm external diameter, thickness of metal 20mm is rotating at 180rpm. The angle of twist of 3m length was found to be 0.7 . Calculate the power transmitted and maximum shear stress induced in the material. Take G = 80
. Calculate the power transmitted and maximum shear stress induced in the material. Take G = 80 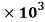 Mpa.
Mpa.
Ans:
Given
D = 200 mm
t = 20 mm
N = 180 rpm
L = 3m = 3000 mm
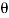 = 0.01222 radian
= 0.01222 radian
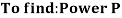
Internal diameter d= D – 2t = 200 - 2 20 = 160 mm
20 = 160 mm
 =
= 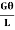
T = 30.2208 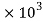 N.M
N.M
Power p = 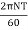 = 569.65 KW
= 569.65 KW
Key takeaways:
- A member which subjected to couple which produce rotation about its longitudinal axis is known as Twisting moment or Torsion.
- Due to Torque applied on shaft, the shaft produce shear stress and shear strain in the material
- In practice, torque are produce in shaft of motors or power equipments e.g. Fans, axles of vehicles, pumps, etc.
Torsion is the twisting of a beam beneath the movement of a torque (twisting moment). It is systematically implemented to screws, nuts, axles, power shafts etc, and is likewise generated extra randomly beneath provider situations in vehicle bodies, boat hulls, plane fuselages, bridges, springs and plenty of different systems and components.
Torsion is the twisting of a beam below the motion of a torque (twisting moment). It is systematically implemented to screws, nuts, axles, force shafts etc, and is likewise generated extra randomly below carrier situations in automobile bodies, boat hulls, plane fuselages, bridges, springs and plenty of different systems and components. A torque, T has the equal units (N m) as a bending moment, M. Both are the fabricated from a pressure and a distance.
In the case of a torque, the pressure is tangential and the space is the radial distance among this tangent and the axis of rotation.
Key takeaways:
- Torsion is the twisting of a beam beneath the movement of a torque (twisting moment).
- It is systematically implemented to screws, nuts, axles, power shafts etc, and is likewise generated extra randomly beneath provider situations in vehicle bodies, boat hulls, plane fuselages, bridges, springs and plenty of different systems and components.
- In the case of a torque, the pressure is tangential and the space is the radial distance among this tangent and the axis of rotation.
1. Strain energy in shear
If t is the uniform shear stress produce in the material by external force applied within elastic limit, the energy stored due to shear loading given by,
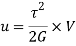
Where
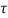 = shear stress
= shear stress
G= modulus of rigidity
Consider a square block ABCD of length l, faces BC and AD are subjected to shear stress let face AD is fixed
The section ABCD will deform to AB1C1D through the angle 
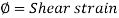


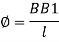
Force P on Face BC1
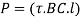
When P is applied gradually gradual load is,
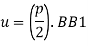

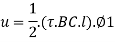
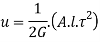
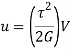
The elastic energy stored due to loading is known as shear resilience.
2. Strain energy in torsion
Let a shaft of period l be below the motion of torque T. Then, the paintings performed in twisting will be same to the stress strength because of torsion (U).
When a member is subjected to a uniform shear stress the strain energy stored in the member is
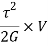
Consider a small element of ring of thickness dr at radius “r”
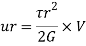
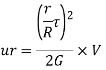
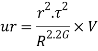
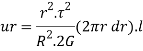

Total strain energy for whole section is obtained by integrating over a range from r=0, to r= D/2 for solid shaft
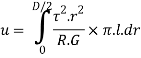
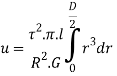
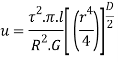
Put limit
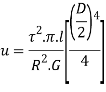
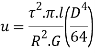
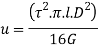
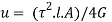
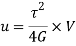
Strain energy due to torsion
Generally, hollow circular shafts are more stronger than solid circular shafts. Torsional rigidity is the product of modulus of rigidity G and polar moment of inertia lp
Torsional = GI Its unit is Nm2.
The electricity of the hole shaft is greater than the identical weight strong shaft.
Hollow shafts have a greater polar second of inertia, which allows them to transmit greater torque than strong shafts.
Hollow shafts do now no longer switch greater electricity however the electricity to weight ratio of hole shafts is greater compared to the strong shaft.
Cases stand up along with in propeller shafts of ships wherein a shaft is subjected to direct thrust similarly to bending second and torsion. In such instances the direct stresses because of bending second and the axial thrust should be combined right into a single resultant.
- Direct stress:
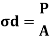
Where,
P= axial thrust
A= Area of cross section
2. Bending stress
Where,
M= Bending moment
I = Moment of inertia
3. Torsion Stress
Where,
T= Torque
R= Radius of shaft
J= polar moment of inertia
Combined Stresses:
Under combination of these stresses,
- Principle Stress
2. Maximum shear stress
Equivalent Moment and Torque
Equivalent bending second can be defined because the bending second with the intention to produce the identical direct pressure as produced by the bending second and torque appearing separately. Similarly, the equivalent torque can be defined because the torque which will produce the identical most shear pressure as produced by the bending second and torque appearing separately.
For a circular shaft of diameter, d = 2r
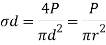
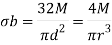
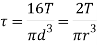
Power transmitted by a shaft
Torque= power (P) x 60 /2n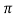
Where power is measured in watts and n is the speed in rpm
Closed Coiled Helical Springs: Designed to withstand stretching and twisting, these springs also are referred to as tension/extension springs.
These springs function a watch or a hook on the stop for attachment. These springs can undergo strain because of excessive torsion or bending
Spring is a vital element in nearly every machinery. These springs perform specific features in specific applications.
These take in shocks in vehicles jogging on choppy roads.
These shop power in toys and circuit breakers.
These deliver cushion impact in sofas and cars.
Springs are of various sorts particularly close and open coiled helical springs, laminated and spiral springs.
This spring is subjected to both axial load and axial couple.
The parameters to be studied in springs are stress, stiffness, deflection and resilience.
Key takeaway:
- These take in shocks in vehicles jogging on choppy roads.
- These shop power in toys and circuit breakers.
- These deliver cushion impact in sofas and cars.
There are particularly varieties of trying out completed on substances named Mechanical trying out and Non-damaging trying out. Here, handiest mechanical trying out might be discussed.
Mechanical Testing Mechanical trying out is a damaging form of trying out that makes use of static or dynamic forces to show the residences of the material. Mechanical trying out consists of the one-of-a-kind varieties of trying out which includes Tensile take a look at, hardness trying out, effect take a look at, fatigue take a look at, creep take a look at, bend take a look at, etc.
- Tensile trying out: This take a look at is completed at the regular trying out machines (UTM). In this take a look at, the specimen is subjected to uni axial tensile pressure in a managed manner till its failure.
- This take a look at facilitates us in getting access to the subsequent residences ductility, yield strength, tensile strength, Young's modulus (E), and Poisson's ratio (μ).
A conventional trying out system (UTM), additionally called a conventional tester substances trying out system or substances take a look at frame, is used to check the tensile power and compressive power of substances. An in advance call for a tensile trying out system is a tens meter.
The "conventional" a part of the call displays that it may carry out many fashionable tensile and compression exams on substances, components, and structures (in different words, that it's far versatile).
Key takeaways:
- Tensile trying out: This take a look at is completed at the regular trying out machines (UTM). In this take a look at, the specimen is subjected to uni axial tensile pressure in a managed manner till its failure.
- This take a look at facilitates us in getting access to the subsequent residences ductility, yield strength, tensile strength, Young's modulus (E), and Poisson's ratio (μ).
1. Testing of hardness:
Hardness is the resistance of a metallic to the penetration of every other tougher frame which does now no longer receive a everlasting set. Hardness Tests is composed in measuring the resistance to plastic deformation of layers of metals close to the floor of the specimen i.e. there are Ball indentation Tests. Ball indentation Tests: This method is composed in pressing a hardened steel ball under a constant load P into a specially organized flat floor at the check specimen as indicated within side .
After removing the load an indentation remains on the floor of the check specimen. If area of the round floor within side the indentation is denoted as F sq. Mm.
Brinell Hardness range is described as:

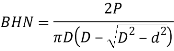
Is expressed in phrases of D and d
Where,
D = ball diameter
d = diametric of indentation and Brinell Hardness range is given by
Then is there may be additionally Vicker's Hardness Number wherein the ball is of conical shape.
2. Impact strength
Static tension assessments of the un notched specimen's do not always reveal the susceptibility of metal to brittle fracture. This crucial component is decided in effect assessments. In effect assessments we use the notched specimen'
This specimen is located on its helps on anvil in order that blow of the striker is contrary to the notch the effect power is described because the strength A, required to rupture the specimen
Impact Strength = A / f
Where
f = It is the cross – phase place of the specimen in cm2 at fracture & manifestly at notch.
The effect power is a complicated feature which takes under consideration each longevity and power of a material. The main purpose of notched – bar checks is to study the simultaneous effect of stress awareness and excessive speed load software Impact check are of the severest kind and facilitate brittle friction.
Impact power values can't be as but be used for layout calculations however those checks as rule supplied for in specs for carbon & alloy steels.
Further, it is able to be cited that during effect checks fracture can be both brittle and ductile. In the case of brittle fracture, fracture happens by separation and is not accompanied by noticeable plastic deformation as happens within side the case of ductile fracture.
Key takeaways:
- Static tension assessments of the un notched specimen's do not always reveal the susceptibility of metal to brittle fracture.
- This crucial component is decided in effect assessments. In effect assessments we use the notched specimen'
- This specimen is located on its helps on anvil in order that blow of the striker is contrary to the notch the effect power is described because the strength A, required to rupture the specimen
References:
- Timoshenko, S. And Young, D. H., “Elements of Strength of Materials”, DVNC, New York USA.
- Kazmi, S. M. A., “Solid Mechanics” TMH, Delhi, India.
- Hibbeler, R. C. Mechanics of Materials. 6th ed. East Rutherford, NJ: Pearson Prentice Hall, 2004
- Crandall, S. H., N. C. Dahl, and T. J. Lardner. An Introduction to the Mechanics of Solids 2nd ed. New York, NY: McGraw Hill, 1979
- Laboratory Manual of Testing Materials - William Kendrick Hall
- Mechanics of Materials - Ferdinand P. Beer, E. Russel Johnston Jr., John T. DEwolf – TMH 2002.