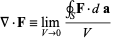UNIT 4
ELECTROMAGNETISM
In physics, we deal with two kinds of quantities – scalars and vectors.
A scalar is an entity which only has a magnitude – no direction. Examples of scalar quantities include mass, electric charge, temperature, distance, etc.
A vector, on the other hand, is an entity that is characterized by a magnitude and a direction. Examples of vector quantities are displacement, velocity, magnetic field, etc.
A scalar can be depicted just by a number, for e.g. a temperature of 300 K. On the other hand, vectorial quantities like acceleration are usually denoted by a vector. Given a vector V, the magnitude of the corresponding quantity can be calculated as the magnitude of the vector itself ∥V∥, while the direction would be specified by a unit vector in the direction of the original vector,
=
.
For example, consider a displacement of (3
+4
+5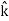
)m, where , as per standard convention, 
,
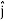and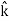
represent unit vectors in the X, Y and Z directions respectively. Therefore, it can be concluded that the distance travelled is ∥3
+4
+5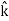
∥ m = 5
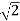m. The direction of travel is given by the unit vector 
+
+
.
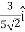Scalar Fields
If we consider temperature within a solid then we have a scalar field since temperature is a scalar quantity and by a scalar field, we mean that there are a set of values of a scalar that must be assigned throughout a continuous region of space. Again this field may be time-dependent if heat is being supplied to the solid. Physical quantities like electric potential, gravitational potential, temperature, density, etc. are expressed in the form of scalar fields.
Graphically scalar fields can be represented by contours which are imaginary surfaces drawn through all points for which field has the same value. For the temperature field, the contours are called isothermal surfaces or isotherms. In the case of electrostatics, if we put a point charge at any place, then electric potential around it will depend on the position of the point. Since the electric potential is a scalar quantity, the field around the charge will be known as a scalar potential field. If all such points at which potential is constant is joined by a surface then such a surface is called equipotential surface.
Such surfaces are also called level surfaces, each level surface having its own constant value. Two-level surfaces cannot cut each other because if they do so then scalar values corresponding to both must hold along their common line which contradicts our definition. Thus scalar point functions i.e. φ(x,y,z)are single-valued functions.
Vector Fields
Like scalar fields, we also have vector fields in which a vector is given for each point in space. As an example consider a fluid flowing along a tube of varying cross-section. In this case, if we specify the fluid velocity at each point, we obtain a vector field, which may be dependent on time if the pressure difference across the tube is varied with time.
The intensity of the electric field, magnetic field, and gravitational field, etc. are examples of a vector field. A vector field is represented at every point by a continuous vector function say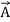 
(x,y,z). At any specific point of the field, the function 
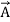(x,y,z)gives a vector of definite magnitude and direction, both of which changes continuously from point to point throughout the field region.
Graphically vector fields are represented by lines known as field or flux lines. These lines are drawn in the field in such a way that tangent at any point of the line gives the direction of a vector field at that point. To express the magnitude of the vector field at any point first draw an infinitesimal area perpendicular to the field line. The number of field lines passing through this area element gives the magnitude of the vector field. One more important thing here to note is that the lines representing vector fields cannot cross, because if they cross they would give non-unique field direction at the point of interaction.
In general, a field is a vector or scalar quantity that can be specified everywhere in space as a function of position. In this module, we deal with 3-dimensional spaces only. Hence, a field is defined as a function of the x, y and zcoordinates corresponding to a location in 3D space.
For example, temperate in 3 dimensional space (a temperature field) can be written as T(x,y,z) a scalar function of the position. An example of a scalar field in electromagnetism is the electric potential.
In a similar manner, a vector field can be defined as a vectorial function of the location (x,y,z)of any point in space.
For instance, every point on the earth may be considered to be in the gravitational force field of the earth. We may specify the field by the magnitude and the direction of acceleration due to gravity (i.e. force per unit mass)g(x,y,z)at every point in space.
To give an example from electromagnetism, consider an electric potential of form 2x2y, a scalar field in 3D space. The corresponding conservative electric field can be computed as the gradient of the electric potential function, and expressed as 4xy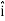
+2x2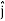
. The magnitude of this electric field can in turn be expressed as a scalar field of the form 
.
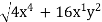GRADIENT
The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that
The term "gradient" is typically used for functions with several inputs and a single output (a scalar field). Yes, you can say a line has a gradient (its slope), but using "gradient" for single-variable functions is unnecessarily confusing. Keep it simple.
“Gradient” can refer to gradual changes of colour, but we’ll stick to the math definition. You’ll see the meanings are related.
PROPERTIES OF THE GRADIENT
Now that we know the gradient is the derivative of a multi-variable function, let’s derive some properties.
The regular, plain-old derivative gives us the rate of change of a single variable, usually x. For example, dF/dx tells us how much the function F changes for a change in x. But if a function takes multiple variables, such as x and y, it will have multiple derivatives: the value of the function will change when we “wiggle” x (dF/dx) and when we wiggle y (dF/dy).
We can represent these multiple rates of change in a vector, with one component for each derivative. Thus, a function that takes 3 variables will have a gradient with 3 components:
The gradient of a multi-variable function has a component for each direction.
And just like the regular derivative, the gradient points in the direction of greatest increase.
However, now that we have multiple directions to consider (x, y and z), the direction of greatest increase is no longer simply “forward” or “backward” along the x-axis, like it is with functions of a single variable.
If we have two variables, then our 2-component gradient can specify any direction on a plane. Likewise, with 3 variables, the gradient can specify and direction in 3D space to move to increase our function.
Gradient tells you how much something changes as you move from one point to another (such as the pressure in a stream). The gradient is the multidimensional rate of change of a particular function. The gradient vector is a representative of such vectors which present the value of differentiation in all the 360° direction for the given point on the curve”
The gradient is a vector function which operates on a scalar function to produce a vector whose scale is the maximum rate of change of the function at the point of the gradient and which is pointed in the direction of that utmost rate of change. The symbol for the gradient is ∇.
Figure 1
(i) A gradient of a scalar quantity is a Vector quantity.
(ii) The magnitude of that vector quantity is equal to the Maximum rate of change of that scalar quantity.
(iii) Change of scalar quantity does not depend only on the coordinate of the point, but also on the direction along which the change is shown.
For the gradient of a vector field, you can think of it as the gradient of each component of that vector field individually, each of which is a scalar. The gradient always points in the direction of the maximum rate of change in a field.
PHYSICAL SIGNIFICANCE OF GRADIENT
A scalar field may be represented by a series of level surfaces each having a stable value of scalar point function θ. The θ changes by a stable value as we move from one surface to another. These surfaces are known as Gaussian surfaces. Now let the two such surfaces are very close together, be represented by two scalar point functions and (θ + d θ). Let ‘r’ and (r + d θ) be the position vectors of points A and B, on the surfaces θ and (θ + d θ) correspondingly with respect to an origin 0 as shown in Figure 2. Clearly, the vector AB will be dr. Let the least detachment between the two surfaces ‘dn’ be in the direction of unit usual vector n at A.
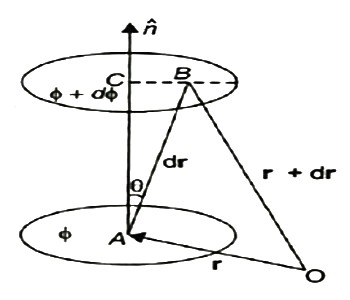
Figure 2
dn = drcos θ
= | n | dr | cosθ =n .dr
Dϕ = ∂ϕ/ dn =∂ϕ/dn n .dr…… (1)
Since the continuous scalar function defining the level surfaces (Gaussian surfaces) has a value θ at point A (x, y, z) and (θ + dθ) at point (x + dx, y + dy, z + dz), we have
dϕ = ∂ ϕ/dx dx +dϕ/∂y + ∂ϕ/∂x dz
= (I ∂ϕ/∂x +j ∂ϕ/vy +k ∂ϕ/∂z) .(idx +jdy +kdz)
= ∆ ϕ. dr … … (2)
From equations (1) and (2), equating the values of d θ,
We obtain ∆θ .dr =∆ϕ= ∂ϕ/ ∂n n .dr
As dr is an arbitrary vector, we have
∆ϕ =∂ϕ/∂ n
Grad ϕ = ∂ ϕ/∂n n
Therefore, the gradient an of a scalar field at any point is a vector field, the scale of which is equal to the highest rate of increase of θ at that point and the direction of it is similar as that of usual to the level surface at that point.
Its physical significance of grad can be understand in terms of the graph of some function z = f(x, y), where f is a reasonable function – say with continuous first partial derivatives. In this case we can think of the graph as a surface whose points have variable heights over the xy – plane. An illustration is given below.
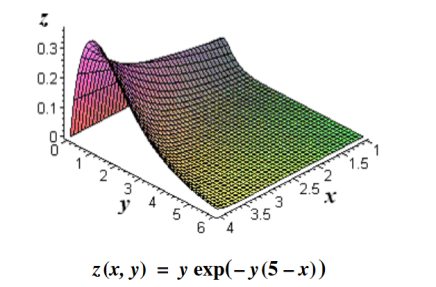
Figure 3
If, say, we place a marble at some point (x, y) on this graph with zero initial force, its motion will trace out a path on the surface, and in fact it will choose the direction of steepest descent. This direction of steepest descent is given by the negative of the gradient of f. One takes the negative direction because the height is decreasing rather than increasing.
Using the language of vector fields, we may restate this as follows: For the given function f(x, y), gravitational force defines a vector field F over the corresponding surfacez = f(x, y), and the initial velocity of an object at a point (x, y) is given mathematically by –∇f(x, y). The gradient also describes directions of maximum change in other contexts. For example, if we think offas describing the temperature at a point(x, y), then the gradient gives the direction in which the temperature is increasing most rapidly.
Divergence and curl are two measurements of vector fields that are very useful in a variety of applications. Both are most easily understood by thinking of the vector field as representing a flow of a liquid or gas; that is, each vector in the vector field should be interpreted as a velocity vector.
Divergence measures the tendency of the fluid to collect or disperse at a point, and curl measures the tendency of the fluid to swirl around the point. Divergence is a scalar, that is, a single number, while curl is itself a vector. The magnitude of the curl measures how much the fluid is swirling, the direction indicates the axis around which it tends to swirl.
DIVERGENCE
Consider water flowing through a large pipe. Now, it has smaller pipes joined to it. Hence, as the water flows, more water is added along the way by the smaller pipes. Hence, the mass flow rate increases as the water flows.
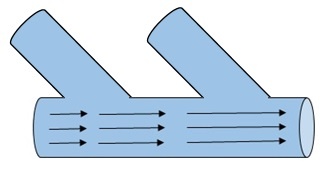
Figure 4
In another case, consider that there is a leakage in the pipe. Hence the mass flow rate decreases as it flows. This change in the flow rate through the pipe, whether it increases or decreases, is called as divergence. Divergence denotes only the magnitude of change and so, it is a scalar quantity. It does not have a direction.
When the initial flow rate is less than the final flow rate, divergence is positive (divergence > 0). If the two quantities are same, divergence is zero. If the initial flow rate is greater than the final flow rate divergence is negative (divergence <0).
Recall that if f is a function, the gradient of f is given by
∇f=⟨∂f/∂x,∂f/∂y,∂f/∂z⟩
Where
∇=⟨∂/∂x,∂/∂y,∂/∂z⟩
The divergence can be defined in terms of this same odd vector ∇ by using the dot product. The divergence of a vector field F=⟨f,g,h⟩ is
Figure 5
PHYSICAL INTERPRETATION OF THE DIVERGENCE
For an electric field:∇·E= ρ/ε, that is there are sources of electric field. Consider a vector field F that represents a fluid velocity: The divergence of F at a point in a fluid is a measure of the rate at which the fluid is flowing away from or towards that point.
A positive divergence is indicating a flow away from the point. ƒPhysically divergence means that either the fluid is expanding or that fluid is being supplied by a source external to the field. ƒThe lines of flow diverge from a source and converge to a sink.
If there is no gain or loss of fluid anywhere then div F= 0. Such a vector field is said to be solenoidal.
Air leaving a punctured tire: Divergence is positive, as closed surface (tire) exhibits net outflow.
CURL
Imagine pouring water in a cup. The water won’t just low linearly but rather, as it reaches the end of the cup, it will flow in a rotational motion before settling in the cup. Or consider water draining down the sink, it will swirl in a rotational motion before going out. If we plot this rotational flow of water as vectors and measure it, it will denote the Curl.
Figure 6
Curl is a measure of how much a vector field circulates or rotates about a given point. when the flow is counter-clockwise, curl is considered to be positive and when it is clock-wise, curl is negative. Sometimes, curl isn’t necessarily flow around a single time. It can also be any rotational or curled vector.
For example, curl can help us predict the voracity, which is one of the causes of increased drag. By using curl, we can calculate how intense it is and reduce it effectively. Calculating divergence helps us understand the flow rate and correct it to suit our needs.
The curl can be defined in terms of this same odd vector ∇ by using the cross product. The curl of a vector field F=⟨f,g,h⟩ is
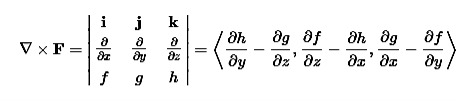
PHYSICAL INTERPRETATION OF THE CURL
Consider a vector field F that represents a fluid velocity:
The curl of F at a point in a fluid is a measure of the rotation of the fluid.
If there is no rotation of fluid anywhere then ∇x F= 0. Such a vector field is said to be irrotational or conservative.
An electrostatic field (denoted by E) has the property ∇xE= 0, an irrotational (conservative) field.
GAUSS DIVERGENCE THEOREM
In vector calculus, divergence theorem is also known as Gauss’s theorem. It relates the flux of a vector field through the closed surface to the divergence of the field in the volume enclosed.
The Gauss divergence theorem states that the vector’s outward flux through a closed surface is equal to the volume integral of the divergence over the area within the surface.
The sum of all sources subtracted by the sum of every sink will result in the net flow of an area. Gauss divergence theorem is the result that describes the flow of a vector field by a surface to the behaviour of the vector field within it.
Let
be a smooth vector field defined on a solid region V with boundary surface A oriented outward. Gauss divergence theorem is given by
The divergence of a vector field F, denoteddiv(F) or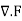
(the notation used in this work), is defined by a limit of the surface integral
| (1) |
where the surface integral gives the value of F integrated over a closed infinitesimal boundary surface S=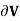
surrounding a volume element V, which is taken to size zero using a limiting process. The divergence of a vector field is therefore a scalar field. If 
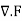=0, then the field is said to be a divergenceless field. The symbol
is variously known as "nabla" or "del."
The physical significance of the divergence of a vector field is the rate at which "density" exits a given region of space. The definition of the divergence therefore follows naturally by noting that, in the absence of the creation or destruction of matter, the density within a region of space can change only by having it flow into or out of the region. By measuring the net flux of content passing through a surface surrounding the region of space, it is therefore immediately possible to say how the density of the interior has changed. This property is fundamental in physics, where it goes by the name "principle of continuity." When stated as a formal theorem, it is called the divergence theorem, also known as Gauss's theorem.
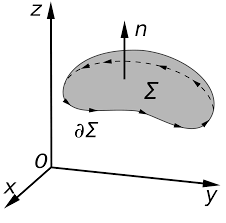
Stokes Theorem
Stokes Theorem is also referred to as the generalized Stokes Theorem. It is a declaration about the integration of differential forms on different manifolds. It generalizes and simplifies the several theorems from vector calculus. According to this theorem, a line integral is related to the surface integral of vector fields.
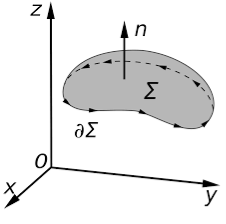
Figure 7
Stokes’ theorem relates the surface integral of the curl of the vector field to a line integral of the vector field around some boundary of a surface. It is named after George Gabriel Stokes. Although the first known statement of the theorem is by William Thomson and it appears in a letter of his to Stokes.
Stoke’s theorem statement is “the surface integral of the curl of a function over the surface bounded by a closed surface will be equal to the line integral of the particular vector function around it.” Stokes theorem gives a relation between line integrals and surface integrals. Depending upon the convenience, one integral can be computed in terms of the other.
Stokes Theorem Formula:
It is,
∮C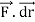 
= ∬S (∇ ×
). 
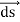
Where,
C = A closed curve.
S = Any surface bounded by C.
F = A vector field whose components are continuous derivatives in S.
Thus, it means that if we walk in the positive direction around C with our head pointing in the direction of n, then the surface will always be on our left. S is oriented smooth surface bounded by a simple, closed smooth-boundary curve C with positive orientation. It can be noted that the surface S can actually be any surface so long as its boundary curve is given by C. This is something that can be used to our advantage to simplify the surface integral on the occasion.
Stokes theorem physics and stokes theorem mathematics are very popular. We can find many applications of stokes theorem in Physics. It helps to derive many useful formulae and equations. For example, stokes theorem in electromagnetic theory is very popular in Physics.
The law was published posthumously in 1867 as part of a collection of work by the famous German mathematician Carl Friedrich Gauss.
Gauss’s law for the electric field describes the static electric field generated by a distribution of electric charges.
It states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
let’s calculate the electric flux through a spherical surface around a positive point charge q, since we already know the electric field in such a situation. Recall that when we place the point charge at the origin of a coordinate system, the electric field at a point P that is at a distance r from the charge at the origin is given by
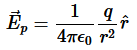
is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 8
.
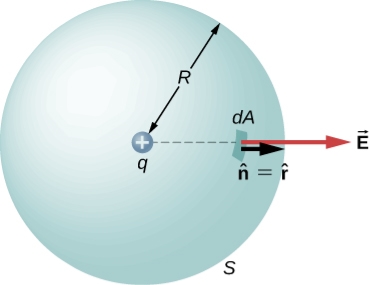
Figure 8: A closed spherical surface surrounding a point charge q.
Then we apply Φ=∫S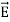
⋅
dA
to this system and substitute known values. On the sphere, 
and r=R
so for an infinitesimal area dA,
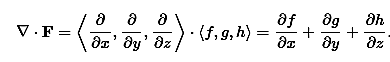
We now find the net flux by integrating this flux over the surface of the sphere
where the total surface area of the spherical surface is 4πR2. This gives the flux through the closed spherical surface at radius ras
Φ=q/ϵ0
A remarkable fact about this equation is that the flux is independent of the size of the spherical surface. This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r2with distance, which just cancels the r2 rate of increase of the surface area.
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
In integral form
in differential form
∇·E = ρ/ε0
But in free space charge ρ is zero so ∇·E =0
FARADAY’S LAW
Faraday’s law of electromagnetic induction (referred to as Faraday’s law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Faraday’s law states that a current will be induced in a conductor which is exposed to a changing magnetic field. Lenz’s law of electromagnetic induction states that the direction of this induced current will be such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it. The direction of this current flow can be determined using Fleming’s right-hand rule.
Let us understand Faraday’s law by faraday‘s experiment.
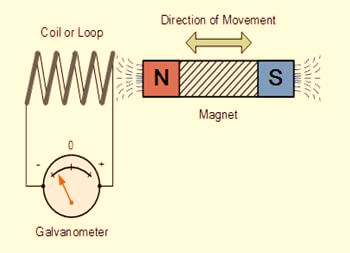
FARADAY’S EXPERIMENT
In this experiment, Faraday takes a magnet and a coil and connects a galvanometer across the coil. At starting, the magnet is at rest, so there is no deflection in the galvanometer i.e. the needle of the galvanometer is at the center or zero position. When the magnet is moved towards the coil, the needle of the galvanometer deflects in one direction.
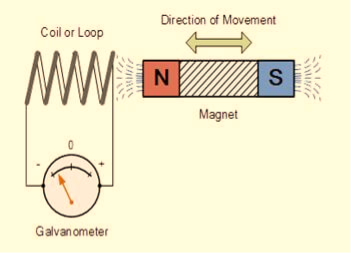
Figure 9
When the magnet is held stationary at that position, the needle of galvanometer returns to zero position. Now when the magnet moves away from the coil, there is some deflection in the needle but opposite direction, and again when the magnet becomes stationary, at that point respect to the coil, the needle of the galvanometer returns to the zero position.
Similarly, if the magnet is held stationary and the coil moves away, and towards the magnet, the galvanometer similarly shows deflection. It is also seen that the faster the change in the magnetic field, the greater will be the induced EMF or voltage in the coil.
Let us take a look at the following table. This table is showing the observation of faraday’s experiment.
Position of magnet | Deflection in galvanometer |
Magnet at rest | No deflection in the galvanometer |
Magnet moves towards the coil | Deflection in galvanometer in one direction |
Magnet is held stationary at same position (near the coil) | No deflection in the galvanometer |
Magnet moves away from the coil | Deflection in galvanometer but in the opposite direction |
Magnet is held stationary at the same position (away from the coil) | No deflection in the galvanometer |
CONCLUSION
From this experiment, Faraday concluded that whenever there is relative motion between a conductor and a magnetic field, the flux linkage with a coil changes and this change in flux induces a voltage across a coil.
Michael Faraday formulated two laws on the basis of the above experiments. These laws are called Faraday’s laws of electromagnetic induction.
FARADAY’S FIRST LAW
Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf and if the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
Method to change the magnetic field:
FARADAY’S SECOND LAW
It states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil. The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
According to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.
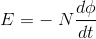………..(9)
Considering Lenz’s Law
Where:
FACTORS ON WHICH INDUCED EMF DEPEND
Displacement current is the rate of change of electric displacement field.
The type of current which passes through a conductor is known as conduction current and is caused by the actual movement of electrons through the conductor. This type of current is mostly used in our day to day life. There is also another kind of current, which is known as displacement current. Displacement current differs from the conduction current because the displacement current does not involve electrons' movement. The displacement current has enormous importance for the propagation of electromagnetic waves. In electromagnetism, displacement current is a quantity appearing in Maxwell's equations that is defined in terms of the rate of change of electric displacement field.
Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do.
It is mathematically represented as
ID = JD S = S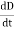 
Where
S = Area of the plate of the capacitor
ID =Displacement current
JD =Displacement current density
D = εE where ε is permittivity of the medium
During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor.
According to Ampere's law, the magnetic field should not present between the plates as there is no current, but in reality, the magnetic field exists there. Maxwell formulated this limitation of Ampere's law by adding a term in the equation of Ampere's law to solve the issue.
Maxwell predicted that the magnetic field will still exist even in the absence of conduction current, and the magnetic field may be associated with the changing electric field. This theory of Maxwell was experimentally proved.
Since the magnetic field is associated with the electric field, the general displacement current formula is given by,
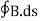= μ0( I+ε0
)
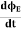This equation is the generalized formula of Maxwell-Ampere law.
Displacement Current Definition
The displacement current (ID) is the part which Maxwell has added to the Ampere's law.
ID = ε0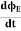
ε0= Permittivity of free space
Derivative of electric flux
Electric flux is the time rate change of flow of the electric field through a surface. If we take the derivative of electric flux, we get the rate of change of the electric field of a given area concerning time.
AMPERE’S LAW
Ampere’s circuital law (ACL) relates current to the magnetic field associated with the current.The magnetic field in space around an electric current is proportional to the electric current which serves as its source, just as the electric field in space is proportional to the charge which serves as its source.
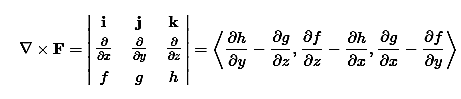
Figure 10
Ampere's Law states that
The integral around a closed path of the component of the magnetic field tangent to the direction of the path equals μ0 times the current intercepted by the area within the path.
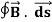= μ0I ………..(1)
Ampere's Law tells that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.
The equation (1) can be written as
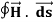= I ………..(2)
Thus the line integral (circulation) of the magnetic field around some arbitrary closed curve is proportional to the total current enclosed by that curve.
In order to apply Ampère’s Law
All currents have to be steady (i.e.do not change with time)
Only currents crossing the area inside the path are taken into account and have some contribution to the magnetic field
Currents have to be taken with their algebraic signs (those going “out” of the surface are positive, those going “in” are negative)-use right hand’s rule to determine directions and signs.
The total magnetic circulation is zero only in the following cases:-
Ampère’s Law can be useful when calculating magnetic fields of current distributions with a high degree of symmetry.
Finally, be aware that the form of Ampère’s Law addressed here applies to magneto statics only. In the presence of a time-varying electric field, the right side of ACL includes an additional term known as the displacement current.
Ampere's Circuital Law
Consider a long thin wire carrying a steady current I. Suppose that the wire is orientated such that the current flows along the z-axis. Consider some closed loop C in the x-y plane which circles the wire in an anti-clockwise direction, looking down the z-axis. Suppose that dr is a short straight-line element of this loop. Let us form the dot product of this element with the local magnetic field 
. Thus,
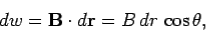……....(3)
Where θ is the angle subtended between the direction of the line element and the direction of the local magnetic field. We can calculate a dw for every line element which makes up the loop C. If we sum all of the dw values thus obtained, and take the limit as the number of elements goes to infinity, we obtain the line integral
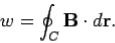…….....(4)
What is the value of this integral? In general, this is a difficult question to answer. However, let us consider a special case. Suppose that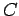 
is a circle of radius 
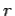centred on the wire. In this case, the magnetic field-strength is the same at all points on the loop. In fact,
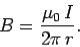……......(5)
Moreover, the field is everywhere parallel to the line elements which make up the loop. Thus,
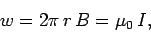…….......(6)
or
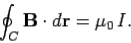……….....(7)
In other words, the line integral of the magnetic field around some circular loop C, centred on a current carrying wire, and in the plane perpendicular to the wire, is equal to μ0 times the current flowing in the wire. Note that this answer is independent of the radius r of the loop: i.e., the same result is obtained by taking the line integral around any circular loop centred on the wire.
In 1826, Ampère demonstrated that Eq. (7) holds for any closed loop which circles around any distribution of currents.
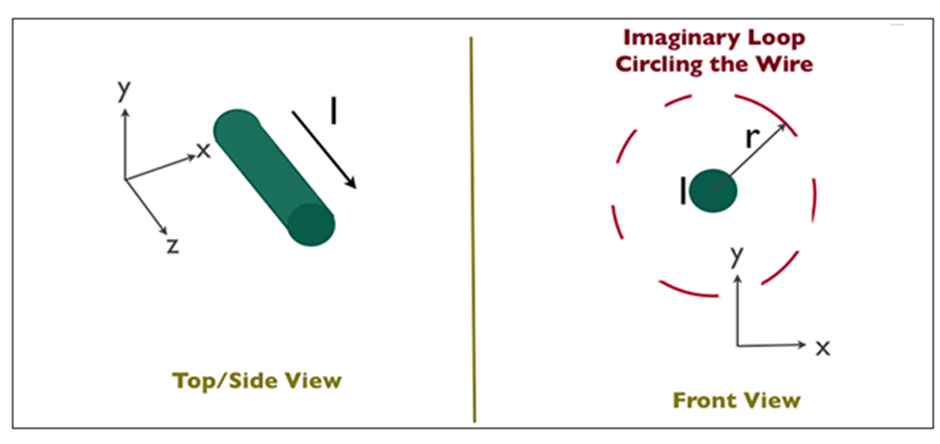
Determining Magnetic Field by Ampere’s Law
Suppose you have a long enough wire that carries a constant current I in amps. How would you determine the magnetic field wrapping the wire at any distance r from the wire?
In the figure below ( Figure11), a long wire exists that carries current in Amps. We need to find out how much is the magnetic field at a distance r. Therefore, we sketch an imaginary route around the wire indicated by dotted blue toward the right in the figure.
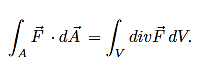
Figure 11
According to the second equation, if the magnetic field is integrated along the blue path, then it has to be equal to the current enclosed, I.
The magnetic field doesn’t vary at a distance r due to symmetry. The path length (in blue) in figure 11 equals to the circumference of a circle, 2πr.
When a constant value H is added to the magnetic field, the equation’s left side looks like this:
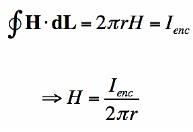
We have figured the magnitude of the field H. Since r is arbitrary, the value of the field H is known.
According to the equation, the magnetic field lowers in magnitude as we move wider. Hence, Ampere’s law can be applied to calculate the extent of the magnetic field surrounding the wire. The field H is a Vector field which reveals that each region has both a direction and a magnitude. The field’s direction is tangential at every point to the imaginary loops as shown in figure12 and the right-hand rule finds the direction of the magnetic field.
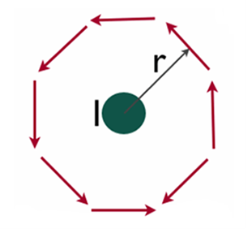
Figure 12
Maxwell Equations
Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.
Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects.
Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.
These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
Maxwell’s first equation (Gauss' Law for Electric Fields)
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
The First Maxwell’s equation (Gauss’s law for electricity)
The Gauss’s law states that flux passing through any closed surface is equal to 1/ε0 times the total charge enclosed by that surface.
Integral form of Maxwell’s 1st equation
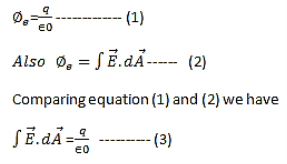
It is the integral form of Maxwell’s 1st equation.
Maxwell’s first equation in differential form
It is called the differential form of Maxwell’s 1st equation.
The Second Maxwell’s equation (Gauss’s law for magnetism)
The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.
we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero.
Why? Why isn't the divergence of B equal to the magnetic charge density?
Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero:
∇·B = 0
Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.
Maxwell’s Third equation (Faraday's Law)
Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.
Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.
∇×E = −∂B/∂t
According to Faraday’s law of electromagnetic induction
It is the differential form of Maxwell’s third equation.
Maxwell’s fourth equation (Ampere's Law)
Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced.
This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon.
The modified form of ampere Law is given by
H.dL=(J+dD/dt)
Take integration on both sides we have
∫H.dL=∫(J+dD/dt).dS
Apply stoke’s theorem to L.H.S. of above equation, we get
∫( ∇xH).dS=∫ H.dL
Now the above equation is written as
∫( ∇xH).dS =∫(J+dD/dt).dS
By cancelling the surface integral on both sides we have
∇xH =J+dD/dt
Which is the differential form of Maxwell’s equation.
This can also be written in the form B
The Ampere-Maxwell Law
Begin with the Ampere-Maxwell law in integral form.
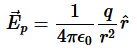
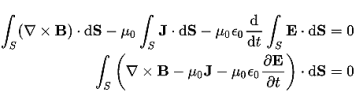
Set the equation to 0.
Physical Significance Of Each Equation
Physical significance of Maxwell’s Ist equation
∇·E = ρ/ε0
According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.
Physical significance of Maxwell’s 2nd equation
∇·B = 0
It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.
Physical significance of Maxwell’s 3rd equation
∇×E = −∂B/∂t
It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.
Physical significance ofMaxwell’s 4th equation
∇×H = J + ∂D/∂t
This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current densityand displacement current density.
Wave is nothing but a pattern of disturbance which propagates and carry energy with it. You can produce a wave on a rope by moving one end of the rope up and down. The wave produces on rope needs a medium to propagate and here medium is rope itself. This type of waves is known as mechanical waves. But in the case of Electromagnetic waves, they don't need a medium to propagate. Electromagnetic waves are waves that are created as a result of variations of electric field and a magnetic field. Or we can say that Electromagnetic waves are nothing but changing magnetic and electric fields. Electromagnetic waves are also known to be solutions of Maxwell's equations. And Maxwell's equations are the fundamental equations of electrodynamics. Electromagnetic waves can transmit energy and travel through a vacuum.
Light waves are examples of electromagnetic waves. Generally, Electromagnetic waves are shown by a sinusoidal graph.
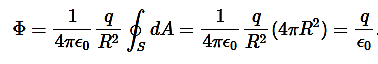
Figure 13
As shown in figure Electromagnetic waves consist of time-varying electric and magnetic fields and they are perpendicular to each other and these both fields are also perpendicular to the direction of propagation of waves.
Maxwell’s four equations are given by
∇·E = ρ/ε0 (1)
∇×E = −∂B/∂t (2)
∇×H = J + ∂D/∂t (3)
∇·B = 0 (4)
These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,
∇=(∂/∂x, ∂/∂y, ∂/∂z)
E is the electric vector
B is the magnetic induction
ρ is the electric charge density
j is the electric current density
ε0 is the permittivity of free space
c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE (5)
D = εE (6)
B = μH (7)
Here,
D is the electric displacement
H is the magnetic vector
σ is the specific conductivity
ε is the dielectric constant (or permittivity)
μ is the magnetic permeability
Free space or non-conducting medium. We know that non conducting medium means no current so conductivity is zero i.e. σ=0
So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below.
(a) No condition current i.eσ=0, thus J=0 ( J=σE)
(b) No charges (i.eρ=0)
For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as
∇.D=0 or ∇.E=0 as ρ=0 (12)
∇ x E= -dB/dt or ∇ x E= -μdH/dt because B = μH (13)
∇x H=d D/dt or ∇ x H = εdE/dt (J=0) and D = εE (14)
∇.B=0 (15)
WAVE EQUATION IN TERMS OF ELECTRIC FIELD INTENSITY, E
Now taking curl of second Maxwell’s equation (13) ,we get
∇x(∇ x E)=- μd/dt (∇ x H)
Applying standard vector identity, that is [∇ *(∇*E)=∇(∇.E)-∇2E] on left hand side of above equation, we get
∇ (∇ .E)-∇2E= -μd/dt (∇x H) (16)
Substituting equations (13) and (14) in equations (16) ,we get
-∇2E= – μεd/dt (dE/dt)
Or ∇2E=με d 2 E/dT2 (17)
Equation (17) is the required wave equation in terms of electric field intensity, E for free space . This is the law that E must obey.
WAVE EQUATION IN TERMS OF MAGNETIC FIELD INTENSITY, H
Take curl of fourth Maxwell’s equation (14) ,we get
∇x(∇xH)=ε d/dt(∇xE)
Applying standard vector identity that is
[∇*(∇*H)=∇ (∇.H)-∇2H]
On left side of above equation , we get
∇(∇.H)-∇2H= ε d/dt(∇xE) (18)
Substituting equations (14) and (13) in equation(18) ,we get
-∇2H= – μεd/dt(dH/dt)
Or
∇2H=με d2H/dt2 (19)
Equations (19) is the required wave equation in terms of magnetic field intensity, H and this is the law that H must obey
For vacuum μ=μ0 and ε=ε0, equations (17) and (19) will become
∇2 E=μ0ε0 d2E/dt2 (20)
And ∇2H= μ0ε0 d2H/dt2 (21)
This leads to an expression for the velocity of propagation
From equation both equations (20) and (21) have the form of the general wave equation for a wave
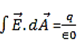
(x,t) traveling in the x direction with speed v. Equating the speed with the coefficients, we derive the speed of electric and magnetic waves, which is a constant that we symbolize with “c”
It is useful to note that in vacuum
c2=1/ε0μ0
Where μ0 is the permeability of free space
Let us rewrite the equation (20) and (21) for one dimension.
Or d 2 E/dx2 =μ0ε0 d 2 E/dt2 (22)
d2H/dx2= μ0ε0 d2H/dt2 (23)
The simplest solutions to the differential equations (22) and (23) are sinusoidal wave functions:
E(x) = Emaxcos(kx-t) (24)
B(x) = Bmaxcos(kx-t) (25)
where k = 2π/λis the wavenumber , ω = 2πƒ is the angular frequency, λ is the wavelength, f is the frequency and ω /k=f=v= c.
A wave’s energy is proportional to its amplitude squared. This is true for waves on guitar strings, for water waves, and for sound waves. In electromagnetic waves, the amplitude is the maximum field strength of the electric and magnetic fields. So the energy of electromagnetic field is proportional to its amplitude squared (E2 or B2).
The electric field describes an electromagnetic wave completely in free space. The magnetic field is related to the electric field by a simple relationship. Start from Faraday's law.
∇ x E= -dB/dt
From left side . Substitute the one dimensional wave equation for electricity and find its curl.
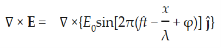
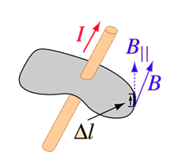
From right side, Substitute the one dimensional wave equation for magnetism and find its time derivative.
Set the two sides equal. Cancel the cosine terms and some other stuff. We will get
E0 = fB0
After Rearranging it
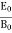=fλ
And we knowthatfλ is the speed of light. So the above equation can be written as
= c
This knowledge can then be used to simplify the energy density situation a bit. Start with the magnetic energy density and replace it with an expression containing the electric field.
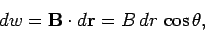
Recall that the speed of light is related to the permeability and permittivity constants.
c =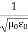 
So
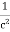= μ0ε0
Thus
ηB =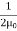 
μ0ε0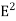 
= 
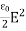
It's the electric energy density. For an electromagnetic wave in free space, half the energy is in the electric field and half is in the magnetic field
η = ηE + ηB
η =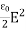 
+
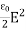
This gives us this compact equation for the total energy densityof an electromagnetic wave.
η = ε0E2
or this one, if you prefer to state things in terms of the magnetic field instead
η =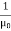 
B2
This is an interesting and simple set of relations, but keeps in mind that it only works for electromagnetic waves in free space. Things are different in a media and the electric and magnetic fields can have any values they want if they're static (meaning there's no accelerating charges).
Since waves are spread out in space and time, energy density is often a more useful concept than energy.
When electromagnetic wave travels in space, it carries energy and energy density is alwaysassociated with electric fields and magnetic fields.
The rate of energy travelled through per unit area i.e. the amount of energy flowing throughper unit area in the perpendicular direction to the incident energy per unit time is called Poyntingvector.
Mathematically Poynting vector is represented as
= 
=(
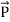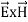) (i)
The direction of Poynting vector is perpendicular to the plane containing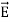 
and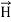
. Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer 
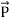is perpendicular to both 
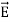and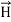
. It represents the rate of energy transfer per unit area.
UNIT
Its unit is W/m2.
Poynting Theorem
Poynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.
i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of charge
Note(Proof is not in your syllabus this is for your knowledge, just remember the final result)
Proof
The energy density carried by the electromagnetic wave can be calculated using Maxwell's equations
div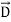
= 0 ...(i)
div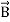
=0 ...(ii)
Curl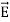 
= - 
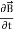…(iii)
Curl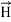 
= 
+ 
…(iv)
Taking scalar product of (3) with H and (4) with 
i.e. 
curl 
= - 
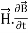……(v)
and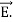
curl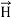 
= 
+ 
. 
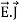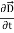…..(vi)
Doing (vi) – (v) i.e.
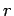
So from equation (vii)
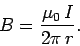
Or
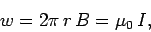
Integrating equation (viii) over a volume V enclosed by a Surface S
Total power leaving the volume = rate of decrease of stored e.m. energy -ohmic power dissipated due to charge motion
This equation (ix) represents the Poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses.
In equation (ix) 
.ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.
The term represent
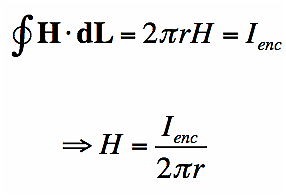
the energy stored in electric and magnetic fields respectively and their sum denotes the total energy stored in electromagnetic field. So total terms gives the rate of decrease of energy stored in volume V due to electric and magnetic fields.
Gives the rate of energy transferred into the electromagnetic field.
This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.
