1.1 Systems Properties Process State Cycle Internal energy Enthalpy

BME

Unit 1

Thermodynamics

1.1 Systems, Properties, Process, State, Cycle, Internal energy, Enthalpy

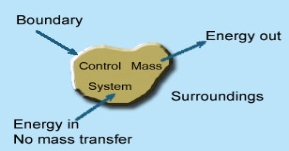
System

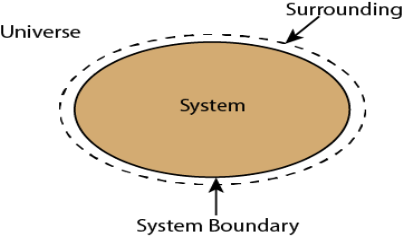
Whenever a change is to be analysed it is essential to specify the region in which the change take place. This is done by drawing a boundary around the region. Boundary may be real or imaginary.

Everything within the boundary is called the system. The region outside the boundary is called surroundings

There are three types of Thermodynamics systems:

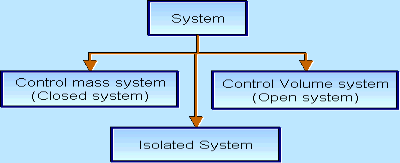
Objectives_template

1 – Open system (control volume system): If mass and energy both cross the boundary of a system it is called open system .in open system both mass and energy can transfer across the boundaries and the mass within the system may not be constant .most of the engineering devices are open systems involving flow of fluids through them.

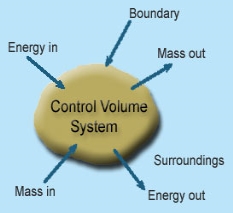
Objectives_template

Example of open system

Boiler – In boiler water convert from liquid to vapor phase. So, mass and energy both transfer the boundary.

Hydraulic turbine wheel – In this device potential energy of water convert into mechanical works. Water enters the wheel from head race side and leaves it to the tail race from the other end, and as such mass cross the system boundary.

Motor-car engine – The engine sucks charge which is mixture of air and petrol and finally exhausts the gases to the surrounding atmosphere.

2 – Closed system (control mass system): If the mass within the boundary of the system does not change, it is called closed system. A closed system does not allow any mass transfer across the boundary but allow transfer of energy across the boundary.

Objectives_template

Example of closed system

Piston cylinder assembly –the gas can reject or receive heat, expand or contract but no mass cross the boundary of system.

Ignition system – electric energy cross the boundary to cause a spark between electrodes an initiate combustion .there is heat transfer but not mass across the system.

Pressure cooker, refrigerator, ice cream freezer etc. are the example of closed system.

3 - Isolated system: Neither mass nor energy cross the boundary of a system .it is called an isolated system. In this no mass and energy cross the system

Objectives_template

Example of isolated system

Universe can be considered as an isolated system

Fluid enclosed in a perfectly insulated closed vessel (thermos flask)

State:

The application of thermodynamic principles begins by defining a system that is in some sense distinct from its surroundings. For example, the system could be a sample of gas inside a cylinder with a movable piston, an entire steam engine, a marathon runner, the planet Earth, a neutron star, a black hole, or even the entire universe. In general, systems are free to exchange heat, work, and other forms of energy with their surroundings.

A system’s condition at any given time is called its thermodynamic state. For a gas in a cylinder with a movable piston, the state of the system is identified by the temperature, pressure, and volume of the gas. These properties are characteristic parameters that have definite values at each state and are independent of the way in which the system arrived at that state. In other words, any change in value of a property depends only on the initial and final states of the system, not on the path followed by the system from one state to another. Such properties are called state functions. In contrast, the work done as the piston moves and the gas expands and the heat the gas absorbs from its surroundings depends on the detailed way in which the expansion occurs.

The behaviour of a complex thermodynamic system, such as Earth’s atmosphere, can be understood by first applying the principles of states and properties to its component part in this case, water, water vapour, and the various gases making up the atmosphere. By isolating samples of material whose states and properties can be controlled and manipulated, properties and their interrelations can be studied as the system changes from state to state.

Path:

If all the change of states of system are plotted and all the points are conned, then the line joining the change of states of the system is called the path

Process:

Thermodynamics process represents a transition in which a system changes from one state to another. When the path is completely specified then the change of state is called a process. A Process is defined as the transformation of the system from one fixed state to another fixed state .When any one of the properties changes, the working substance or system is said to have undergone a process.

Some of the processes are identified by special names as given below:

Isobaric process (constant pressure process)

Isochoric process (constant volume process)

Isothermal process (constant temperature process)

Isentropic process (constant entropy process)

Adiabatic process(perfectly insulated process)

Enthalpy:

In thermodynamics process constant enthalpy means that enthalpy does not change in all process. Best understand the concept of constant enthalpy we should understand the throttling process.

Throttling Process:

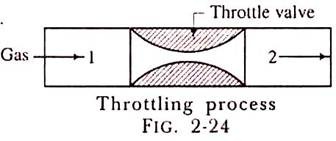
The throttling process is an expansion process in which the pressure reduces after expansion and the velocity is negligible. A throttling expansion occurs when a gas or a vapour is expanded through an aperture of minute dimensions such as a throat or a slightly opened valve.

During the throttling process the expanding fluid is forced through the aperture by its pressure but the hole is so narrow that the frictional resistance between the fluid and the wall reduces the fluid velocity to a negligible amount; as a result, the fluid escapes with a small amount of kinetic energy.

Due to friction kinetic energy reappears as heat and the gas is raised to its initial temperature. During a throttling process no heat is supplied or rejected, no external work is done and in the case of a perfect gas there is no alteration in temperature.

When a fluid expands through a throttle valve or a constricted orifice, the enthalpy before the throttling valve is equal to the enthalpy after throttling. This does not mean, however, that the throttling process is constant enthalpy process. Here the properties before and after the process are defined. Fig. 2-24 shows throttling process.

H1 = H2.

In this process the enthalpy remains constant. The enthalpy at condition 1 is equal to enthalpy at condition 2.

Internal Energy:

As usual, we get change in internal energy = U2 – U1 = m x Cv (T2 – T1).

Another way of determination of change in internal energy is very common in isentropic operation.

By first law of thermodynamics as applied to non-flow process,

Heat supplied = change in internal energy + work done; but heat supplied is zero

Change in internal energy = – work done.

Thus, we get an important relation in an isentropic process. This relation can be stated as “Change in internal energy is numerically equal to work done”. When the work is done by the gas, it loses internal energy and it gains internal energy when the work is done on the gas.

Cycle:

When a system goes through different change of states and return backs to the original state, i.e., all the properties are identical to the original state, then the system is said have gone through a thermodynamic cycle.

1.2 Zeroth Law, First law and Second Law of Thermodynamics

Zeroth Law of thermodynamics

If two systems are each in thermal equilibrium with the third system then the two systems are in thermal equilibrium which each other.

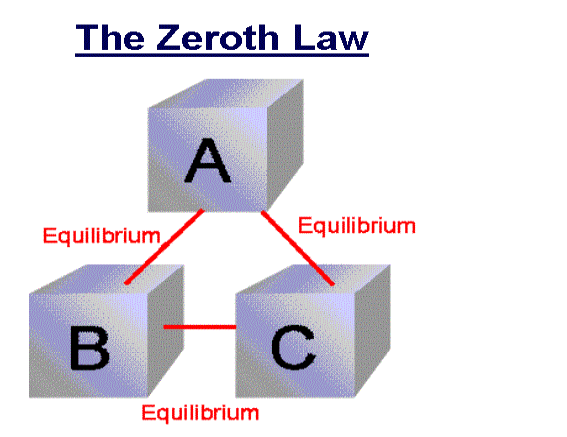
Description: Zeroth Law of Thermodynamics | Thermodynamics, Modern physics, Physics

When a body A is in thermal equilibrium with a body B , and also separately with a body C ,then B and C will thermal equilibrium with each other .this is known as the Zeroth law of thermodynamics.

First law of Thermodynamics

Sometimes our body start to sweat and feel warm when we are in a room full of people and the sweating becomes excessive if the room size is small. This happens because our body is trying to cool off hence heat transfers from our body in the form of ‘sweat’. This entails the first law of thermodynamics.

The first law of thermodynamics states that the total energy of an isolated system is constant. Energy can be transformed from one form to another, but can neither be created nor destroyed.

According to this law, some of the heat given to system is used to change the internal energy while the rest in doing work by the system. Mathematically,

ΔQ=ΔU+ΔW

Where,

ΔQ = Heat supplied to the system

ΔW= Work done by the system.

ΔU = Change in the internal energy of the system.

If Q is positive, then there is a net heat transfer into the system, if W is positive, then there is work done by the system. So positive Q adds energy to the system and positive W takes energy from the system.

It can also be represented as ΔU=ΔQ−W

We can say that internal energy tends to increase when heat is given to the system and vice versa.

Limitations of First Law of Thermodynamics

The limitation of the first law of thermodynamics is that it does not say anything about the direction of flow of heat.

It does not say anything whether the process is a spontaneous process or not.

The reverse process is not possible. In actual practice, the heat doesn’t convert completely into work. If it would have been possible to convert the whole heat into work, then we could drive ships across the ocean by extracting heat from the water of the ocean.

Statement of Second law of thermodynamics

The second law of thermodynamics can be understood by following two statements.

Kelvin-Planck statement

It is impossible to convert all the heat extracted from a hot body into work. In the heat engine, the working substance takes heat from the hot body, converts a part of it into work and gives the rest to the cold body. There is no engine that can convert all the heat taken from the source into work, without giving any heat into the sink. This means that for obtaining continuous work, a sink is necessary.

Clausius statement

It is not at all possible to transfer heat from a cold body to a hot body without the expenditure of work by an external energy source or its states that the heat energy cannot transfer from a body at a lower temperature to a body at a higher temperature without the addition of energy.

For example - There is a refrigerator that transfers an amount of heat from a cold body to a hot body without having any supply of external energy. So this is the violation of Clausius statement. Now suppose an engine working between the same hot and cold bodies takes in heat from hot body converts a part W into work and gives the remaining heat to the cold body.

The engine alone does not violate the second law of thermodynamics. But if the engine and refrigerator combine together, they form a device that takes up all the heat from the hot body and converts all into work without giving up any amount to the cold body. Its violets the Kelvin-Planck statement. So we say that the two statements of the second law of thermodynamics are equal in all respects

1.3 Basic Concept of Entropy

Entropy, the measure of a system’s thermal energy per unit temperature that is unavailable for doing useful work. Because work is obtained from ordered molecular motion, the amount of entropy is also a measure of the molecular disorder, or randomness, of a system. The concept of entropy provides deep insight into the direction of spontaneous change for many everyday phenomena.

The idea of entropy provides a mathematical way to encode the intuitive notion of which processes are impossible, even though they would not violate the fundamental law of conservation of energy. For example, a block of ice placed on a hot stove surely melts, while the stove grows cooler. Such a process is called irreversible because no slight change will cause the melted water to turn back into ice while the stove grows hotter. In contrast, a block of ice placed in an ice-water bath will either thaw a little more or freeze a little more, depending on whether a small amount of heat is added to or subtracted from the system. Such a process is reversible because only an infinitesimal amount of heat is needed to change its direction from progressive freezing to progressive thawing. Similarly, compressed gas confined in a cylinder could either expand freely into the atmosphere if a valve were opened (an irreversible process), or it could do useful work by pushing a moveable piston against the force needed to confine the gas. The latter process is reversible because only a slight increase in the restraining force could reverse the direction of the process from expansion to compression. For reversible processes the system is in equilibrium with its environment, while for irreversible processes it is not.

To provide a quantitative measure for the direction of spontaneous change, Clausius introduced the concept of entropy as a precise way of expressing the second law of thermodynamics. The Clausius form of the second law states that spontaneous change for an irreversible process in an isolated system (that is, one that does not exchange heat or work with its surroundings) always proceeds in the direction of increasing entropy. For example, the block of ice and the stove constitute two parts of an isolated system for which total entropy increases as the ice melts.

By the Clausius definition, if an amount of heat Q flows into a large heat reservoir at temperature T above absolute zero, then the entropy increase is ΔS = Q/T. This equation effectively gives an alternate definition of temperature that agrees with the usual definition. Assume that there are two heat reservoirs R1 and R2 at temperatures T1 and T2 (such as the stove and the block of ice). If an amount of heat Q flows from R1 to R2, then the net entropy change for the two reservoirs is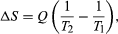 entropy equation

which is positive provided that T1 > T2. Thus, the observation that heat never flows spontaneously from cold to hot is equivalent to requiring the net entropy change to be positive for a spontaneous flow of heat. If T1 = T2, then the reservoirs are in equilibrium, no heat flows, and ΔS = 0.

The condition ΔS ≥ 0 determines the maximum possible efficiency of heat engines—that is, systems such as gasoline or steam engines that can do work in a cyclic fashion. Suppose a heat engine absorbs heat Q1 from R1 and exhausts heat Q2 to R2 for each complete cycle. By conservation of energy, the work done per cycle is W = Q1 – Q2, and the net entropy change is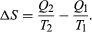 entropy equation

To make W as large as possible, Q2 should be as small as possible relative to Q1. However, Q2 cannot be zero, because this would make ΔS negative and so violate the second law. The smallest possible value of Q2 corresponds to the condition ΔS = 0, yielding entropy equation as the fundamental equation limiting the efficiency of all heat engines. A process for which ΔS = 0 is reversible because an infinitesimal change would be sufficient to make the heat engine run backward as a refrigerator.

The same reasoning can also determine the entropy change for the working substance in the heat engine, such as a gas in a cylinder with a movable piston. If the gas absorbs an incremental amount of heat dQ from a heat reservoir at temperature T and expands reversibly against the maximum possible restraining pressure P, then it does the maximum work dW = P dV, where dV is the change in volume. The internal energy of the gas might also change by an amount dU as it expands. Then by conservation of energy, dQ = dU + P dV. Because the net entropy change for the system plus reservoir is zero when maximum work is done and the entropy of the reservoir decreases by an amount dSreservoir = −dQ/T, this must be counterbalanced by an entropy increase of entropy equation for the working gas so that dSsystem + dSreservoir = 0. For any real process, less than the maximum work would be done (because of friction, for example), and so the actual amount of heat dQ′ absorbed from the heat reservoir would be less than the maximum amount dQ. For example, the gas could be allowed to expand freely into a vacuum and do no work at all. Therefore, it can be stated that entropy equation with dQ′ = dQ in the case of maximum work corresponding to a reversible process.

This equation defines Ssystem as a thermodynamic state variable, meaning that its value is completely determined by the current state of the system and not by how the system reached that state. Entropy is an extensive property in that its magnitude depends on the amount of material in the system.

In one statistical interpretation of entropy, it is found that for a very large system in thermodynamic equilibrium, entropy S is proportional to the natural logarithm of a quantity Ω representing the maximum number of microscopic ways in which the macroscopic state corresponding to S can be realized; that is, S = k ln Ω, in which k is the Boltzmann constant that is related to molecular energy.

All spontaneous processes are irreversible; hence, it has been said that the entropy of the universe is increasing: that is, more and more energy becomes unavailable for conversion into work. Because of this, the universe is said to be “running down.”

1.4 Properties of ideal gas

The properties of IDEAL gases are that:

they are compressible

they are always in motion, colliding elastically within a container

they take the shape of the container

they behave inertly

The IDEAL gases are compressible in the sense that because they have so much energy, it makes it easy to force them to move in an inward direction, thereby compressing them.

The IDEAL gases are always in motion, colliding elastically with the container, meaning that they lose no energy after collisions and thus can keep moving.

The IDEAL gases take the shape of the container as a result of their compressibility, and so the volume of the container can be assumed to be the overall volume of the gas(es) inside.

The IDEAL gases behave inertly, meaning that they are assumed to not react with each other. This keeps things simple, so that their properties can be studied in the absence of complications where the gases could have been used up in gas reactions.

1.5 Properties of pure substances

Properties of Pure Substance

A pure substance is a material with homogeneous and invariable composition.

Pure substances can have multiple phases, an ice water mixture is still a pure substance but an air-steam is not a pure substance.

Pure Substance:

A substance that has a fixed chemical composition throughout is called a pure substance i.e., water, nitrogen, helium, and CO2.

Substances which are mixture of various elements or compounds also qualify as pure substances as long as mixture is homogeneous.

Saturation Temperature and Saturation Pressure:

At given pressure, the temperature at which a pure substance changes phase is called the saturation temperature Tsat.

Likewise at a given temperature, the pressure at which a pure substance changes phase is called the saturation pressure psat.

Example: For water at a pressure of 101.325 kPa, Tsat is 100oC, conversely at a temperature of 100oC, psat is 101.325 kPa.

Latent Heat:

The amount of energy absorbed or released during a phase change process is called the latent heat.

The amount of energy absorbed during melting is called the latent heat of vaporization.

Similarly, the amount of energy absorbed during vaporization is called latent heat of vaporization and is equivalent to the energy released during condensation.

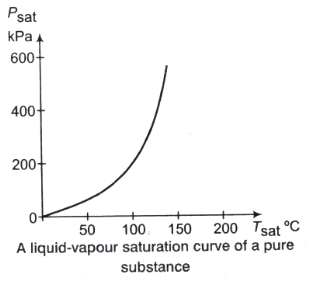
Liquid-Vapour Saturation Curve:

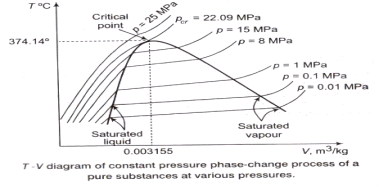
From the following figure, it is clear that Tsat increases with psat. Thus, a substance at higher pressure will boil at higher temperatures.

Tsat = f(psat)

In the kitchen, higher boiling temperature means shorter cooking time and energy saving.

The atmospheric pressure, and thus the boiling temperature of water, decreases with elevation. Therefore, it takes longer time to cook at higher altitudes than it does at sea level.

Property Diagrams for Phase-change Process

The T-V Diagram:

Consider piston cylinder device containing liquid water at 20oC and 1 atm.

Water will start boiling at a much higher temperature (179.9oC) at inside pressure of the cylinder reaches at 1 MP.

The specific volume of the saturated liquid is larger and the specific volume of the saturated vapour is smaller than the corresponding values at 1 atm pressure. That is, the horizontal line that connects the saturated liquid and saturated vapour states is much shorter.

As the pressure is increased further, this saturation line will continue to get shorter as shown in figure and it will become a point when the pressure reaches 22.09 MPa for the case of water. This point is called the critical point and it is defined as the point at which the saturated liquid and saturated vapour state are identical.

At pressure above the critical pressure, there will not be a distinct phase change. Instead, the specific volume of the substance will continually increase and at all times there will be only one phase present. It is customary to refer to the substance as superheated vapour at temperature above the critical temperature and as compressed liquid at temperatures below the critical temperature.

The p-V Diagram:

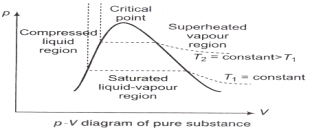
The general shape of the p-V diagram of a pure substance is very much like the T-V diagram but the T = constant lines on this diagram have a downward trend.

Consider again a piston cylinder device that contains liquid water at 1 MPa and 150°C, water at this state exists as a compressed liquid. Now, the weights on top of the piston are removed one by one so that the pressure inside the cylinder decreases gradually.

The water is allowed to exchange heat with the surroundings so its temperature remains constant.

As the pressure decreases, the volume of the water will increase slightly, when the pressure reaches the saturation pressure volume at the specific temperature, the water will start to boil.

During this vaporisation process, both the temperature and the pressure remain constant but the specific volume increases. Once the last drop of liquid is vaporised further reduction in pressure results in a further increase in specific volume.

If the process is repeated for other temperatures similar paths will be obtained for the phase change processes.

Triple Phase:

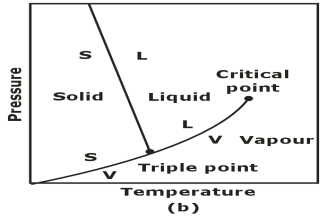
When all three phases of a pure substance co-exist in equilibrium. It is called triple phase.

Triple phase states form a line called the triple line.

The triple line appears as a point on the p-T diagram and therefore is often called the triple point.

No substance can exist in the liquid phase in stable equilibrium at pressure below the triple point pressure.

The same can be said for temperature for substance that contract on freezing.

Substances at high pressure can exist in the liquid phase at temperatures below the triple point temperature.

The p-T Diagram:

Solid – Liquid = Fusion

Liquid – Vapour = Vaporisation

Solid – Vapour = Sublimation

Enthalpy

Enthalpy is a measure of the total energy of a thermodynamic system.

It includes energy required to create a system and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.

For certain type of processes particularly in power generation and refrigeration.

Enthalpy (H )= U + pV(kJ) Or
per unit mass h = u + pV(kJ/kg)

Saturated Liquid and Saturated Vapour States:

Subscript f → properties of saturated liquid

Subscript g → properties of saturated vapour

Vf → specific volume of saturated liquid

Vg → specific volume of saturated vapour

Vfg → difference between Vg and Vfnthal

Vfg = Vg - Vf

hfg → enthalpy of vaporisation or latent heat of vaporisation (amount of energy need to vaporise a unit mass of saturated liquid at a given temperature of pressure).

The magnitude of latent heat depends on temperature and pressure at which phase change occurs.

For example at 1 atm pressure, the latent heat of fusion of water is 333.7 kj/kg and latent heat of vaporization is 2257.1 kj/kg.

At below triple point pressure, substance begins to change directly gas.

Enthalpy of vaporization decreases as the temperature or pressure increases and become zero at the critical point.

Saturated Liquid Vapour Mixture:

During vaporisation process, a substance exists as part liquid and part vapour.

A new property quality x is the ratio of mass of vapour to the total mass of the mixture.

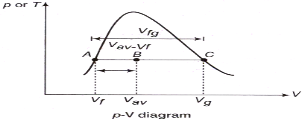
Quality or dryness fraction:

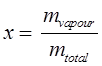
mtotal = mliquid + mvapour = mf + mg

Where, mf = mass of the saturated liquid, and mg = mass of the saturated vapour

Quality has significance for saturated mixtures only.

It has no meaning in the compressed liquid or superheated region.

Its value lie between 0 (saturated liquid) and 1 (saturated vapour).

The properties of the saturated liquid are the same whether it exists alone or in a mixture with saturated vapour.

During vaporization process, only the amount of saturated liquid changes not its properties. The same can be said about a saturated vapour.

Quality:

Vav = (1-x)Vf + xVg or Vav = Vf + xVg

Uav = Uf + Ufg

hav = hf + xhfg

Superheated Vapour:

Since, the superheated region is a single phase region (vapour phase only) temperature and pressure are no longer dependent properties and they can conveniently be used as the two independent properties.

Superheated vapour is characterised by:

Lower pressures (p < psat at a given T)

Higher temperatures (T < Tsat at a given p)

Higher specific volumes (U > Vg at a given p or T)

Higher internal energies (U > Ug at a given p or T)

Higher enthalpies (h > hg at a given p or T)

Compressed Liquid

A compressed liquid may be approximated as a saturated liquid at the given temperature.

This is because the compressed liquid properties depend on temperature much more strongly than they do on the pressure.

V ≅ Vf
u ≅ uf
h ≅ hf

In general, a compressed liquid is characterised by:

Higher pressures (p > psat at a given T)
Lower temperatures (T < Tsat at a given p)
Lower specific volumes (V <Vf at a given p or T)
Lower internal energies (U < Uf at a given p or T)
Lower enthalpies (h < hf at a given p or T)

The Ideal Gas Equation of State

Any equation that relates the pressure, temperature and specific volume of a substance is called an equation of state.

Property relations that involve other properties of a substance at equilibrium states are also referred to as equation of state.

Ideal gas equation of state: pV = RT, where, p = Absolute pressure, T = Absolute temperature, and V = Specific volume

Gas and vapour are often used as synonymous words.

The vapour phase of a substance is customarily called a gas when it is above the critical temperature.

Vapour usually implies a gas that is not far from a state of condensation.

Gas Constant

It has been experimentally observed that the ideal gas relation given closely approximately the p-V-T behaviour of real gases at low densities.

At low pressure and high temperature, the density of a gas decreases and the gas behaves as an ideal gas under these conditions.

Where, Ru = Universal gas constant, M = Molar mass, R = Gas constant.

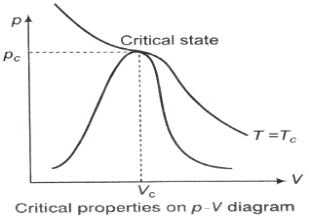
Compressibility Factor

Compressibility factor (correction factor) is measurement of deviation of gases from ideal gas behaviour.

Compressibility factor (z):

It can also be expressed as

For ideal gases ⇒ z = 1

For real gases ⇒ z is away from unity (> 1 or < 1)

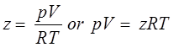
Reduce Pressure and Temperature

Gases behave differently at a given temperature and pressure, but they behave very much the same at temperature and pressures normalized with respect to their critical temperatures and pressures.

The normalization is done as introducing new terms,

Reduce pressure:

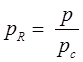
and reduce temperature:

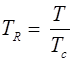
Where, Tcr = critical temperature, pcr = critical pressure.

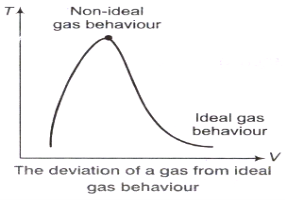
z factor for all gases is approximately the same at the same reduced pressure and temperature is greatest in the vicinity of the critical point.

Gases deviate from the ideal gas behaviour most in the neighbourhood of the critical point. So, we can say that at critical point. Compressibility factor is constant for all substances.

As mention above z factor for all gases is approximately the same at the same reduced pressure and temperature.

Pseudo reduced specific volume (VR) :

VR is defined differently from pR and TR. It is related to Tcr and pcr instead of Vcr.

All substances have same critical compressibility factor

Experimental value of Zc for most substances fall within a narrow range of 0.20 – 0.33.

Z the compressibility factor is the same function of pr and Tr for all gases.

Specific heat all constant pressure and volume are the properties of the substances and are always properties.

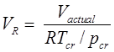
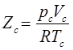
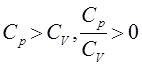
Van der wall’s Equation of State:

Two effects: Inter molecular attraction forces:

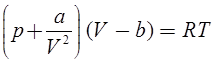
and b accounts for volume occupied by the gas molecules.

Virital Equation of State:

Van der Waal’s equation of state can be expressed in the virital form as given below

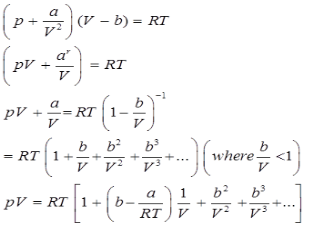
This is called the virital equation of state.

1.6 Steam formation, Types of Steam, Enthalpy, Specific volume

Enthalpy

The total heat content of a substance is called enthalpy. Actually it has much broad definition in thermodynamics but for 1st year BME students this definition works just fine. So, total heat content by steam is termed as its enthalpy. It is denoted by ‘H’. SI unit is KJ

‘h‘ is generally used term which represents specific enthalpy, unit for which is KJ/Kg.
In steam tables you will see enthalpy written as hi, hg, hig

hi is the enthalpy of liquid that is water at boiling point that’s why subscript ‘l’ is used, point ‘D’ in h-T diagram. Similarly hg is enthalpy of dry saturated steam, point ‘E’ in h-T diagram and hig is the latent heat, Process D to E in h-T diagram

Specific volume:

Gases (steam is a gas) occupy less space under higher pressure than under lower pressure. This means 1 kilogram of steam occupies different volumes, depending upon its pressure. The term specific volume refers to the volume that one kg of steam occupies at a given pressure and temperature.

Unit is m3 / kg denoted by v

Types of Steam

Steam for Indirect Heating

Saturated Steam

Saturated steam is the steam which is completely dry and has same temperature as the water from which it is formed. When we start boiling the water, its temperature goes on increasing till it reaches the boiling point at that pressure.

If further heat is added to the water, it converts to steam after absorbing the latent heat of evaporation. This steam, which exists at same temperature as that of the water is called as saturated steam. If saturated steam does not contain even slightest amount of water droplets, it is called as dry saturated steam.

Vacuum steam

As we all know, at a particular pressure, saturated steam always exists at the boiling point of water at that pressure. Saturated steam exists roughly at 100 Deg. C. at atmospheric pressure. As we go on increasing the pressure, the boiling point of water also goes up and hence, the temperature of saturated also goes up.

What will happen to the temperature of saturated steam if we go on reducing the pressure instead of increasing it? Logical answer is, the temperature at which saturated steam will be formed will also go down. This steam, which is generated at sub-atmospheric pressure (vacuum conditions) is called as vacuum steam. Vacuum steam has temperature below 100 Deg. C.

Let us take an example where we have to heat a fluid which is at 30 Degrees to 80 Degrees. The task can be accomplished by using hot water or vacuum steam of suitable temperature. Using vacuum steam is an expensive affair as vacuum pump will be required to create vacuum.

On the other hand, in case of heating with water, the temperature of water will go on decreasing as it will be losing its sensible heat. Hence, a larger heat transfer area is required. In case of vacuum steam, there is transfer of latent steam with high heat transfer coefficients and will require lower heat transfer area. As vacuum steam heats the fluid by losing its latent heat, the heating will take place at same temperature.

Steam for Power Generation

Superheated Steam

If saturated steam is further heated, its temperature goes on increasing beyond the boiling point. Such steam, with temperature higher than the boiling point at that pressure is called as superheated steam.

It is always recommended to use saturated steam for process application and superheated steam for power generation purpose.

Steam for Injection (Direct Heating)

Clean Steam (also referred to as clean steam, WFI steam, high purity steam, sanitary clean steam, pharmaceutical clean steam, GMP clean steam and pyrogen free steam) is similar to clean steam; however, the resulting condensate must meet the standards of USP grade water for injection (WFI) and contain no bacteria or pyrogens. Pure steam must be produced by a pure steam generator; which is classed as sanitary in design, or from a multiple effect still.

1.7 Internal energy and dryness fraction of steam, use of Steam tables

Internal energy and dryness fraction of steam

Internal energy may be considered a thermodynamic property. Internal energy is an extensive property because it depends on the mass of the system. Similarly, kinetic and potential energies are extensive properties. Internal energy may at times refer to both internal energy per unit mass and the total energy.

From the lesson Conservation of Energy, raising the temperature of a body increases its internal energy; lowering the body's temperature decreases its internal energy. Therefore, change in internal energy can often be associated with a change in temperature. In the absence of motion, gravity, surface effects, electricity, or other effects, the state of a pure substance is specified by two independent properties. It is very significant that, with these restrictions, the internal energy may be one of the independent properties of a pure substance. This means, for example, that if the pressure and internal energy are specified (with reference to an arbitrary base) of superheated steam, the temperature is also specified. Thus, in a table of thermodynamic properties such as the steam tables, the value of internal energy can be tabulated along with other thermodynamic properties. Most thermodynamic tables should list the internal energy for saturated states. Included should be the internal energy of saturated liquid uf and the internal energy of saturated vapor ufg. The values are given in relation to an arbitrarily assumed reference state, which, for water in the steam tables, is taken as zero for saturated liquid at the triple-point temperature, 0.01°C. All values of internal energy in the steam tables are then calculated relative to this reference (note that the reference state cancels out when finding a difference in u between any two states). Values for internal energy are found in the steam tables in the same manner as for specific volume. In the liquid–vapor saturation region:

U = Uliq + Uvap

or:

mu = mliquf + mvapug

Dividing by m and introducing the quality x gives:

u = (1 − x)uf + xug

u = uf + xufg

As an exmaple, the specific internal energy of saturated steam having a pressure of 0.6 MPa and a quality of 95% can be calculated as:

u = uf + xufg = 669.9 + 0.95(1897.5) = 2472.5 kJ/kg

In thermostatic, the only energy in a substance is that stored in a system by molecular activity and molecular bonding forces. This is commonly denoted as internal energy. A commonly accepted adjustment to this static situation for fluid flow is to add two more energy terms that arises from Newtonian mechanics.

In the study of thermodynamics, it is convenient to consider the bulk kinetic and potential energy separately and then to consider all the other energy of the control mass in a single property that we call the internal energy. The kinetic and potential energy of the control mass are associated with the coordinate frame that is selected and can be specified by the macroscopic parameters of mass, velocity, and elevation. The internal energy U includes all other forms of energy of the control mass and is associated with the thermodynamic state of the system.

Steam is said to be dry saturated when at that particular pressure its temperature is equal to the boiling point. It is difficult to produce dry saturated steam in practice and steam will often contains water droplets. So steam generated in the drum of the boiler is often wet and contains some moisture. If the moisture content of the steam is 7% by mass, then the dryness fraction of the steam is said to be 0.93 and that means the steam is only 93% dry.
Evaporation Enthalpy of wet steam is expressed as a product of specific enthalpy (hfg) and dryness fraction (x). Heat content of the wet steam and dry saturated steam are different. Dry saturated steam is having higher heat content (useable energy) than the wet steam.

Actual Enthalpy of Evaporation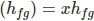
Actual total Enthalpy of wet steam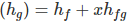

Where, hf is Liquid Enthalpy.
Density of water is higher than that of the steam, so the specific volume of the water is far lesser than that of the specific volume of the steam.
Thus the droplets of water in the wet steam will occupy negligible-space and the specific volume of the wet-steam is less than that of the dry steam and given by the formula:
Actual specific volume = x vg
Where, vg is the specific volume of dry saturated steam

Steam Phase Diagram

Relation of enthalpy and temperature corresponding to different pressure range is graphically represented in Phase Diagram.

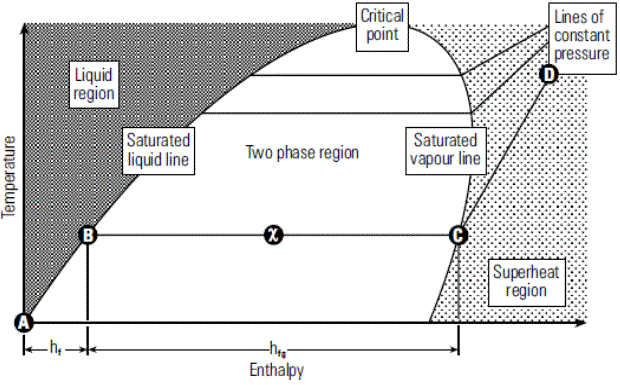
enthalpy curve

Liquid Enthalpy (hf) on Phase Diagram

When water is heated from 0oC to its saturation temperature at atmospheric pressure it follows the saturated liquid line until it has received all its liquid enthalpy hf and is represented by (A-B) on Phase diagram.

Enthalpy of Saturated Steam (hfg)

Any further heat addition results in change in phase to saturated steam and is represented by (hfg) on phase diagram i.e B-C

Dryness Fraction (x)

When heat is applied then the liquid start changing its phase from liquid to vapour and then the dryness fraction of the mixture starts increasing i.e moving towards unity. In the phase diagram dryness fraction of the mixture is 0.5 at exactly mid of the line B-C. Similarly at point C on the phase diagram dryness fraction value is 1.

Line C-D

Point C is in the saturated vapour line, any further heat addition results in increasing the steam temperature i.e beginning of steam super-heating represented by line C – D.

Liquid Zone

Region towards left side of the saturated liquid line.

Super Heat Zone

Region towards right side of the saturated vapour line.

Use of steam table:

The thermodynamics steam tables contain the following tables:

Saturated water and steam temperature tables: In these tables for every temperature the absolute pressure, specific volume for saturated water and saturated steam, specific enthalpy for saturated water and saturated steam and specific entropy for saturated and saturated steam are given.

Saturated water and steam pressure tables: In these tables for every pressure the temperature, specific volume for saturated water and saturated steam, specific enthalpy for saturated water and saturated steam and specific entropy for saturated and saturated steam is given.

Specific volume of superheated steam: In this table for every pressure the saturation temperature and the specific volume at various temperatures are given.

Enthalpy of superheated steam: In this table for every pressure the saturation temperature and the enthalpy of superheated steam at various temperatures are given.

Entropy of superheated steam: In this table for every pressure the saturation temperature and the entropy of superheated steam at various temperatures are given.

Specific volume of superheated steam: In this table at every absolute pressure the specific volume of supercritical steam is given.

Enthalpy of supercritical steam: In this table at every absolute pressure the enthalpy of supercritical steam is given.

Entropy of supercritical steam: In this table at every absolute pressure the entropy of supercritical steam is given.

How to Use the Steam Table

In steam tables the properties of the dry steam are listed and for the wet steam the properties may be calculated from the steam tables of the dry and saturated steam.

For values that are not listed exactly in the tables, the value between two figures can be obtained by linear interpolation. Interpolation is a mathematical tool by which, depending on the interval between two variables, a value in between can be calculated.

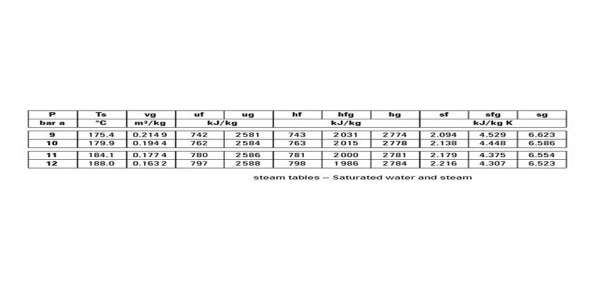Using the Thermodynamics Steam Table: Crucial Tool for Engineers The steam table shown above is a saturated water and steam table. As all the other tables are used on the same principle we will only discuss this one. For an absolute pressure of 9 bars, the saturation temperature is 175.4 C. It means that at a temperature of 175.4 and above C all of the steam will be saturated. Of course, any temperature above this will be super heating of the steam.

It must be noted however that at 175.4 C, depending on the latent heat supplied for vaporization, the steam can have any dryness faction. vg is the specific volume of steam, hf is the specific enthalpy of water, hg is the specific enthalpy of steam, sf is the specific entropy of water, and sg is the specific entropy of steam.

We will now become familiar with this formula:

h = hf + xL

Where x is dryness fraction and L = hg – hf

By the above formula, if we know the dryness fraction of steam, we can calculate the enthalpy of wet steam, and its value would lie between that of the saturated water and saturated steam.

For example if the dryness fraction is 0.8 for steam at 9 bars absolute pressure in bars.

Referring to the steam table above, hf = 743 kJ/Kg, L = 2031 kJ/Kg,

h = 743 + 0.8 x 2031 = 2367.8 kJ/Kg

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined