Unit – 2
Adversarial Search
Adversarial search is a sort of search that examines the problem that arises when we attempt to plan ahead of the world while other agents plan against us.
● In previous topics, we looked at search strategies that are purely associated with a single agent attempting to find a solution, which is often stated as a series of activities.
● However, in game play, there may be moments when more than one agent is looking for the same answer in the same search field.
● A multi-agent environment is one in which there are multiple agents, each of which is an opponent to the others and competes against them. Each agent must think about what another agent is doing and how that activity affects their own performance.
● Adversarial searches, also referred to as Games, are searches in which two or more players with conflicting goals try to find a solution in the same search space.
● The two fundamental variables that contribute in the modeling and solving of games in AI are a Search problem and a heuristic evaluation function.
Types of Games in AI
● Perfect information: A game with perfect information is one in which agents have complete visibility of the board. Agents can see each other's movements and have access to all game information. Examples include chess, checkers, go, and other games.
● Imperfect information: Tic-tac-toe, Battleship, blind, Bridge, and other games with incomplete information are known as such because the agents do not have all of the information and are unaware of what is going on.
● Deterministic games: Deterministic games have no element of chance and follow a strict pattern and set of rules. Examples include chess, checkers, go, tic-tac-toe, and other games.
● Non-deterministic games: Non-deterministic games are those with a number of unpredictable events and a chance or luck aspect. Dice or cards are used to introduce the element of chance or luck. These are unpredictably generated, and each action reaction is unique. Stochastic games are another name for these types of games.
Example: Backgammon, Monopoly, Poker, etc.
Key takeaway
● The mini-max algorithm is a recursive or backtracking method in decision-making and game theory. It offers the optimum course of action for the player, assuming that the opponent is also performing well.
● Recursion is used by the Mini-Max algorithm to search the game tree.
● The Min-Max algorithm is mostly used in AI for game play. Examples include chess, checkers, tic-tac-toe, go, and other two-player games. The current state's minimax choice is calculated using this algorithm.
● In this method, the game is played by two players, one named MAX and the other named MIN.
● Because the opponent player receives the smallest benefit while they receive the highest profit, both players are fighting it.
● Both players in the game are opponents, with MAX choosing the highest value and MIN choosing the lowest.
● The minimax method employs a depth-first search technique to investigate the whole game tree.
● The minimax algorithm descends all the way to the tree's terminal node, then backtracks the tree recursively.
Pseudo code for MIN - MAX Algorithm
function minimax(node, depth, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, false)
maxEva= max(maxEva,eva) //gives Maximum of the values
return maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, true)
minEva= min(minEva, eva) //gives minimum of the values
return minEva
Optimal decision in multiplayer games
A dependent strategy, which defines MAX's move in the initial state, then MAX's movements in the states resulting from every probable response by MIN (the opponent), and so on, is the optimal solution in adversarial search.
One move deep: If a game ends after one MAX and MIN move each, we say the tree is one move deep, with two half-moves, each referred to as a ply.
Minimax value: The node's minimax value is the utility (for MAX) of being in the corresponding state, assuming that both players play optimally from there until the game ends. The minimax value of a terminal state determines its utility.
Given a game tree, the optimal strategy can be computed using the minimax value of each node, i.e., MINIMAX (n).
MAX likes to get to the highest value state, whereas MIN prefers to go to the lowest value state.
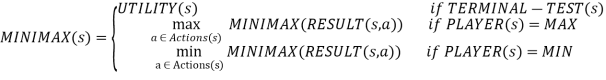
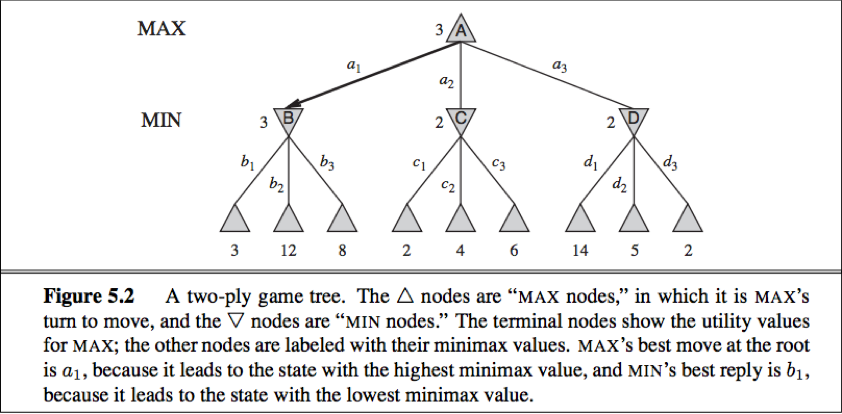
Fig 1: Two ply game tree
Multiplayer games
Each node's single value must be replaced by a vector of values. A vector VA, VB, VC> is associated with each node in a three-player game with players A, B, and C, for example.
From each actor's perspective, this vector indicates the utility of a terminal circumstance.
In nonterminal states, the backed-up value of a node n is always the utility vector of the successor state with the highest value for the player choosing at n.
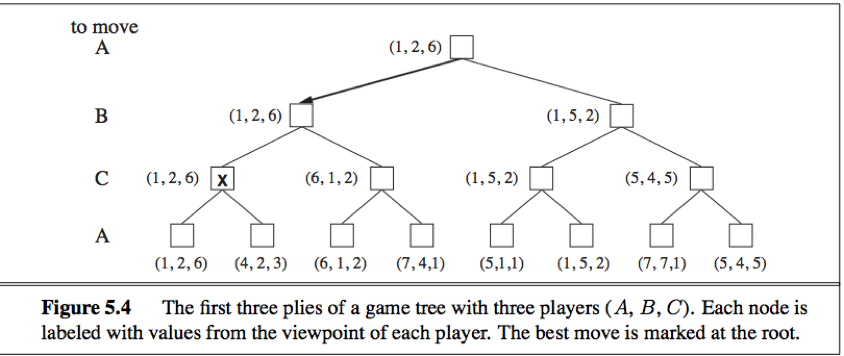
Fig 2: Three piles of a game tree with three players (A, B, C)
Key takeaway
● Alpha-beta pruning is a modified version of the minimax approach. It's a way to make the minimax algorithm better.
● As we observed with the minimax search approach, the number of game state that the minimax search algorithm must explore grows exponentially with the depth of the tree. We won't be able to eliminate the exponent, but we can cut it in half. As a result, we may compute the correct minimax choice without having to check each node of the game tree using a technique called pruning. It's called alpha-beta pruning because it involves two threshold parameters for future expansion, Alpha and beta. It's also known as the Alpha-Beta Algorithm.
● Alpha-beta pruning can be done at any level in a tree, and it can also prune the entire subtree as well as the tree leaves in some cases.
● Alpha: At any point along the Maximizer path, this is the best (highest-value) option we've uncovered so far. The value of alpha starts at -∞.
● Beta: At every point along the Minimizer path, this is the best (lowest-value) option we've uncovered thus far. Beta has a value of +∞ in the start.
● The Alpha-beta pruning to a conventional minimax algorithm achieves the same outcome as the usual technique, but it eliminates nodes that don't affect the final decision but slow down the process. As a result, reducing these nodes speeds up the process.
Pseudo code for Alpha beta Pruning
function minimax(node, depth, alpha, beta, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, False)
maxEva= max(maxEva, eva)
alpha= max(alpha, maxEva)
if beta<=alpha
break
return maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, true)
minEva= min(minEva, eva)
beta= min(beta, eva)
if beta<=alpha
break
return minEva
Evaluation function
The quality of a game-playing program's evaluation function determines its performance.
● The terminal states should be arranged in the same order as the true utility function.
● The probability of winning is related to the evaluation of nonterminal states.
● It must not take too long to compute!
Cutting off search
● Modify alpha-beta search so that:
○ Terminal? is replaced by Cutoff?
○ Utility is replaced by Eval
○ if Cutoff-Test (state, depth) then return Eval(state)
○ depth is chosen such that the amount of time used will not exceed what the rules of the game allow
○ Iterative deepening search can be applied
■ When the timer runs out, the move chosen by the deepest completed search is returned.
Key takeaway
● An intelligent agent needs knowledge of the real world in order to make effective decisions and reasoning.
● Knowledge-based agents are capable of retaining an internal state of knowledge, reasoning about it, updating it in response to observations, and acting on it. These agents can represent the world and operate intelligently using some type of formal representation.
● Two major components make up knowledge-based agents:
○ Knowledge-base and
○ Inference system.
The following tasks must be performed by a knowledge-based agent:
● Agents should be able to represent states, actions, and other things.
● A representative new percept should be able to be incorporated.
● The internal representation of the world can be updated by an agent.
● The internal representation of the world can be deduced by an agent.
● An agent can deduce the best course of action.
The Architecture of knowledge-based agents
Fig 3: Architecture of knowledge-based agents
The graphic above shows a general design for a knowledge-based agent. The knowledge-based agent (KBA) collects input from the environment by monitoring it. The agent's inference engine processes the data and communicates with KB to make judgments based on the knowledge contained in KB. The learning component of KBA keeps the knowledge base current by learning new material.
Key takeaway
A logic is a formal language that allows sound inference and has well defined syntax and semantics. There are various logics that allow you to represent various types of things and allow for more or less efficient inference. Different varieties of logic exist, such as propositional logic, predicate logic, temporal logic, and description logic. However, expressing something in logic may not be natural, and conclusions may be ineffective.
Example of logic
Language of numerical constraints:
● A sentence:
x + 3 ≤ z x,
z - variable symbols (primitives in the language)
● An interpretation:
I: x = 5, z = 2
Variables mapped to specific real numbers
● Valuation (meaning) function V:
V (x + 3 ≤ z, I) is False for I: x = 5, z = 2
is True for I: x = 5, z = 10
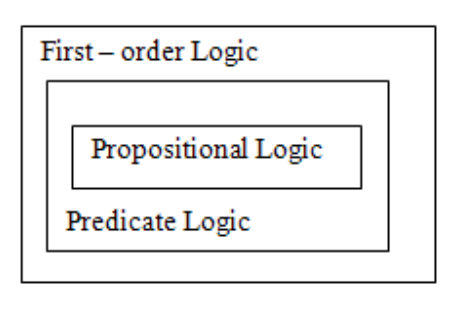
Fig 4: Logic
Types of logic
● Different types of logics possible
● Propositional logic
● First-order logic
● Temporal logic
● Numerical constraints logic
● Map-coloring logic
Key takeaway
Propositional logic is the most basic type of logic, in which all statements are made up of propositions. A declarative statement that can be true or false is referred to as a "proposition." It's a logical and mathematical approach of expressing information.
Sentences can be a bit of a gamble. Boolean reasoning is used in propositional logic to convert our real-world data into a computer-readable structure. "Today is hot and humid," for example, will be misunderstood by the machine. If we can develop propositional logic for this sentence, we can have the machine read and analyze our message.
The notion that all propositions' final output (meaning) is either true or false is at the heart of propositional logic, which is developed from Boolean logic. It's impossible to be both at the same time.
Some basic propositional logic facts are listed below.
● Propositional logic is sometimes known as Boolean logic since it works with 0 and 1.
● In propositional logic, symbolic variables are employed to express the logic, and any symbol, such as A, B, C, P, Q, R, and so on, can be used to represent a proposition.
● Propositions can be true or false at the same moment, but not both.
● Propositional logic is made up of an object, relations or functions, and logical connectives.
● The essential parts of propositional logic are propositions and connectives.
● Connectives are logical operators that link two sentences together.
● Tautology, commonly known as a legitimate sentence, is a proposition formula that is always true.
● Contradiction is a proposition formula that is always false.
● The term "proposition formula" refers to a formula that has both true and false values.
● Propositions are statements that are inquiries, demands, or views, such as "Where is Kabir," "How are you," and "What is your name."
Representation of proposition logic
There are two types of prepositions that can be represented by propositional logic: atomic and complicated prepositions. A single preposition, such as "the sky is blue," "hot days are humid," "water is liquid," and so on, is referred to as atomic.
Complex prepositions are prepositions that are created by joining one, two, or more phrases. In propositional logic, the syntax that represents the link between two or more sentences is made up of five symbols. The structure used to express data is referred to as syntax.
Name | Symbol | Stands for |
Conjunction | 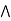 | And |
Disjunction | 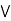 | Or |
Implication | 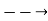 | If-then |
Negation | 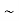 | Not |
Biconditional | 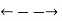 | If and only if |
Fig 5: Logical connectives
Advantages of propositional logic
● The declarative character of propositional logic states that knowledge and inference are different, and that inference is domain-independent.
● Propositional logic is a declarative language since its semantics is based on a truth connection between words and alternative worlds.
● It also has the expressive power to deal with missing data by using disjunction and negation.
Reasoning
Reasoning is the mental activity of drawing logical conclusions and making predictions from available knowledge, facts, and beliefs. "We can state that reasoning is a means to deduce facts from existing evidence." It's a general approach to arriving at valid findings.
Reasoning is essential in artificial intelligence in order for the computer to think rationally and function as well as a human brain.
The process of generating a conclusion from a collection of premises using a system of rules is known as reasoning.
The reasoning process includes thinking, rationally arguing, and forming inferences.
When a system is asked to perform a task for which it has not been given explicit instructions, it must reason. It must infer what it needs to know based on the data it already has.
Numerous different types of reasoning have been discovered and recognized, but there are still many questions about their logical and computational properties.
Popular reasoning processes include abduction, induction, model-based reasoning, explanation, and confirmation.
Types of Reasoning
In artificial intelligence, reasoning can be divided into the following categories:
● Deductive reasoning
● Inductive reasoning
● Abductive reasoning
● Common Sense Reasoning
● Monotonic Reasoning
● Non-monotonic Reasoning
Resolution
Construction of rebuttal proofs, or proofs by contradictions, is a form of theorem proof known as resolution. John Alan Robinson, a mathematician, invented it in 1965.
We use resolutions when numerous statements are provided and we need to show a conclusion from those claims. Unification is a fundamental concept in proofs by resolutions. Resolution is a single inference rule that can efficiently function on both the conjunctive normal form and the clausal form.
Steps for Resolution
Example:
Demonstrate with a resolution that:
f. Peanuts are a favorite of John's.
Key takeaway
● First-order logic is a type of knowledge representation used in artificial intelligence. It's a propositional logic variation.
● FOL is expressive enough to convey natural language statements in a concise manner.
● First-order logic is sometimes known as predicate logic or first-order predicate logic. First-order logic is a complex language for constructing information about objects and expressing relationships between them.
● First-order logic (as does natural language) assumes not just that the world contains facts, as propositional logic does, but also that the world has the following:
○ Objects: People, numbers, colors, conflicts, theories, squares, pits, wumpus,
○ Relation: It can be a unary relation like red, round, or nearby, or an n-any relation like sister of, brother of, has color, or comes between.
○ Functions: Father of, best friend, third inning of, last inning of......
● First-order logic contains two basic pieces as a natural language:
○ Syntax
○ Semantics
Syntax
Syntax has to do with what ‘things’ (symbols, notations) one is allowed to use in the language and in what way; there is/are a(n):
● Alphabet
● Language constructs
● Sentences to assert knowledge
Logical connectives (⇒, ∧, ∨, and ⇐⇒), negation (¬), and parentheses. These will be used to recursively build complex formulas, just as was done for propositional logic.
Constants symbols are strings that will be interpreted as representing objects, e.g., Bob might be a constant.
Variable symbols will be used as “place holders” for quantifying over objects.
Predicate symbols Each has an arity (number of arguments) associated with it, which can be zero or some other finite value. Predicates will be used to represent object characteristics and relationships.
Zero-arity Because predicate symbols are viewed as propositions in first-order logic, propositional logic is subsumed. These assertions can be thought of as world properties.
Predicates with a single parameter can be thought of as specifying object attributes. If Rich is a single-arity predicate, then Rich (Bob) is used to indicate that Bob is wealthy. Multi-arity predicates are used to describe relationships between items.
Formula 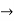 PrimitiveFormula
PrimitiveFormula
| (Formula Connective Formula)
| 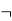 Sentence
Sentence
| Qualifier Variable Formula
PrimitiveFormula 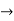 Predicate(Term,…,Term)
Predicate(Term,…,Term)
Term 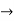 Function(Term,…,Term)
Function(Term,…,Term)
| Constant
| Variable
Connectifier 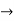
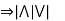
Quantifier 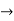
Constant 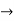 any string that is not used as a variable predicate or function
any string that is not used as a variable predicate or function
Variable 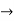 any string that is not used as a constant predicate or function
any string that is not used as a constant predicate or function
Predicate 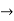 any string that is not used as a constant variable or function
any string that is not used as a constant variable or function
Function 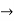 any string that is not used as a constant predicate or constant
any string that is not used as a constant predicate or constant
Function symbols Each has a specific arity (number of input arguments) and is understood as a function that maps the stated number of input objects to objects. Allowing FatherOf to be a single-arity function symbol, the natural interpretation of FatherOf (Bob) is Bob's father.
Zero-arity function symbols are considered to be constants.
Universal and existential quantifier symbols will be used to quantify over objects. For example, ∀ x Alive(x) ⇒ Breathing(x) is a universally quantified statement that uses the variable x as a placeholder.
Semantics of First-Order Logic
As with all logics, the first step in determining the semantics of first-order logic is to define the models of first-order logic. Remember that one of the benefits of using first-order logic is that it allows us to freely discuss objects and their relationships. As a result, our models will comprise objects as well as information about their properties and interactions with other items.
First order model
A first-order model is a tuple hD, Ii, where D denotes a non-empty object domain and I denote an interpretation function. D is nothing more than a collection of items or elements that can be finite, infinite, or uncountable. The interpretation function I gives each of the available constant, function, and predicate symbols a meaning or interpretation as follows:
● If c is a constant symbol, then I(c) is an object in D. Thus, given a model, a constant can be viewed as naming an object in the domain.
● If f is a function symbol of arity n, then I(f) is a total function from Dn to D. That is the interpretation of f is a function that maps n domain objects to the domain D.
● If p is a predicate symbol of arity n > 0, then I(p) is a subset of Dn; that is, a predicate symbol is interpreted as a set of tuples from the domain. If a tuple O = (o1, · · · , on) is in I(p) then we say that p is true for the object tuple O.
● If p is a predicate symbol of arity 0, i.e., a simple proposition, then I(p) is equal to either true or false.
Assume we have a single predicate TallerThan, a single function FatherOf, and a single constant Bob. The following could be a model M1 for these symbols:
D = {BOB, JON, NULL}
I(Bob) = BOB
I(TallerThan) = {hBOB, JONi}
Because I(FatherOf) is a function, we'll only show the value for each argument to give the FatherOf meaning.
I(FatherOf)(BOB) = JON
I(FatherOf)(JON) = NULL
I(FatherOf)(NULL) = NULL
M2 could also be interpreted as follows,
D = { BOB, JON }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi,hJON, BOBi }
I(FatherOf)(BOB) = BOB
I(FatherOf)(JON) = JON
It's vital to highlight the difference between Bob, which is a constant (a syntactic entity), and BOB, which is a domain object (a semantic entity). The second interpretation isn't exactly what we're looking for (the objects are dads of themselves, and TallerThan is inconsistent), but it's still a viable model. By imposing proper limitations on the symbols, the knowledge base can rule out such unexpected models from consideration.
Key takeaway
Inference is used in First-Order Logic to generate new facts or sentences from current ones. It's crucial to understand some basic FOL terms before diving into the FOL inference rule.
Substitution:
Substitution is a fundamental approach for modifying phrases and formulations. All first-order logic inference systems contain it. The substitution becomes more difficult when there are quantifiers in FOL. We refer to the replacement of a constant "a" for the variable "x" when we write F[a/x].
Equality:
Atomic sentences are generated in First-Order Logic not only through the employment of predicate and words, but also through the application of equality. We can do this by using equality symbols, which indicate that the two terms relate to the same thing.
FOL inference rules for quantifier:
Because inference rules in first-order logic are comparable to those in propositional logic, below are some basic inference rules in FOL:
● Universal Generalization
● Universal Instantiation
● Existential Instantiation
● Existential introduction
Universal Generalization:
● Universal generalization is a valid inference rule that states that if premise P(c) is true for any arbitrary element c in the universe of discourse, we can arrive at the conclusion x P. (x).
● It can be represented as: 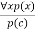
● If we want to prove that every element has a similar property, we can apply this rule.
● x must not be used as a free variable in this rule.
Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.
Universal Instantiation:
● Universal instantiation, often known as universal elimination or UI, is a valid inference rule. It can be used numerous times to add more sentences.
● The new knowledge base is logically equivalent to the previous one.
● We can infer any phrase by replacing a ground word for the variable, according to the UI.
● According to the UI rule, any phrase P(c) can be inferred by substituting a ground term c (a constant inside domain x) for any object in the universe of discourse in x P(x).
● It can be represented as: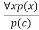
Example: IF "Every person like ice-cream"=> ∀x P(x) so we can infer that
"John likes ice-cream" => P(c)
Existential Instantiation:
● Existential Elimination, also known as Existential Instantiation, is a valid first-order logic inference rule.
● It can only be used once to substitute for the existential sentence.
● Despite the fact that the new KB is not conceptually identical to the previous KB, it will suffice if the old KB was.
● This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
● The only constraint with this rule is that c must be a new word for which P(c) is true.
● It can be represented as:
Existential introduction
● An existential generalization, also known as an existential introduction, is a valid inference rule in first-order logic.
● If some element c in the world of discourse has the characteristic P, we can infer that something else in the universe has the attribute P, according to this rule.
● It can be represented as: 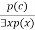
Example: Let's say that,
"Pritisha got good marks in English."
"Therefore, someone got good marks in English."
Propositional vs. First-Order Inference
Previously, inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.
Inference rules for quantifiers:
To get sentences without quantifiers, several inference techniques can be applied to sentences containing quantifiers. We'll be able to make the conversion if we follow these requirements.
Universal Instantiation (UI):
The rule states that by substituting a ground word (a term without variables) for the variable, we can deduce any sentence. Let SUBST () stand for the outcome of the substitution on the sentence a. The rule is then written.
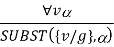
For any v and g ground term combinations. For example, in the knowledge base, there is a statement that states that all greedy rulers are Evil.
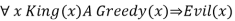
For the variable x, with the substitutions like {x/John}, {x/Richard} the following sentences can be inferred
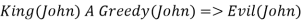
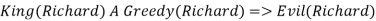
As a result, the set of all potential instantiations can be used to substitute a globally quantified phrase.
Existential Instantiation (EI):
The existential statement states that there is some object that fulfills a requirement, and that the instantiation process is simply giving that object a name that does not already belong to another object. A Skolem constant is the moniker given to this new name. Existential Instantiation is a subset of a broader process known as "skolemization."
If the statement a, variable v, and constant symbol k do not occur anywhere else in the knowledge base,
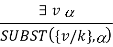
For example, from the sentence
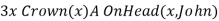
So we can infer the sentence
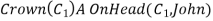
As long as C1 does not appear elsewhere in the knowledge base. Thus, an existentially quantified sentence can be replaced by one instantiation
Elimination of Universal and Existential quantifiers should give new knowledge base which can be shown to be inferentially equivalent to old in the sense that it is satisfiable exactly when the original knowledge base is satisfiable.
Key takeaway
● Unification is the process of finding a substitute that makes two separate logical atomic expressions identical. The substitution process is necessary for unification.
● It accepts two literals as input and uses substitution to make them identical.
● Let Ψ1 and Ψ2 be two atomic sentences and 𝜎 be a unifier such that, Ψ1𝜎 = Ψ2𝜎, then it can be expressed as UNIFY (Ψ1, Ψ2).
● Example: Find the MGU for Unify {King(x), King (John)}
Let Ψ1 = King(x), Ψ2 = King (John),
Substitution θ = {John/x} is a unifier for these atoms, and both phrases will be identical after this replacement.
● For unification, the UNIFY algorithm is employed, which takes two atomic statements and returns a unifier for each of them (If any exist).
● All first-order inference techniques rely heavily on unification.
● If the expressions do not match, the result is failure.
● The replacement variables are referred to as MGU (Most General Unifier).
Example: Let's say there are two different expressions, P (x, y), and P (a, f(z)).
In this example, we need to make both above statements identical to each other. For this, we will perform the substitution.
P (x, y)......... (i)
P (a, f(z))......... (ii)
● Substitute x with a, and y with f(z) in the first expression, and it will be represented as a/x and f(z)/y.
● With both the substitutions, the first expression will be identical to the second expression and the substitution set will be: [a/x, f(z)/y].
Conditions for Unification:
The following are some fundamental requirements for unification:
● Atoms or expressions with various predicate symbols can never be united since they have different predicate symbols.
● Both phrases must have the same number of arguments.
● If two comparable variables appear in the same expression, unification will fail.
Generalized Modus Ponens:
For atomic sentences pi, pi ', and q, where there is a substitution θ such that SU θ, pi) = SUBST (θ, pi '), for all i
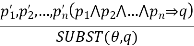
N + 1 premises = N atomic sentences + one implication. Applying SUBST (θ, q) yields the conclusion we seek.
p1’ = King (John) p2’ = Greedy(y)
p1 = King(x) p2 = Greedy(x)
θ = {x / John, y/ John} q = Evil(x)
SUBST (θ, q) is Evil (John)
Generalized Modus Ponens = lifted Modus Ponens
Lifted - transformed from:
Propositional Logic → First-order Logic
Unification Algorithms
Algorithm: Unify (L1, L2)
1. If L1 or L2 are both variables or constants, then:
1. If L1 and L2 are identical, then return NIL.
2. Else if L1 is a variable, then if L1 occurs in L2 then return {FAIL}, else return (L2/L1).
3. Also, Else if L2 is a variable, then if L2 occurs in L1 then return {FAIL}, else return (L1/L2). d. Else return {FAIL}.
2. If the initial predicate symbols in L1 and L2 are not identical, then return {FAIL}.
3. If LI and L2 have a different number of arguments, then return {FAIL}.
4. Set SUBST to NIL. (At the end of this procedure, SUBST will contain all the substitutions used to unify L1 and L2.)
5. For I ← 1 to the number of arguments in L1:
1. Call Unify with the ith argument of L1 and the ith argument of L2, putting the result in S.
2. If S contains FAIL, then return {FAIL}.
3. If S is not equal to NIL, then:
2. Apply S to the remainder of both L1 and L2.
3. SUBST: = APPEND (S, SUBST).
6. Return SUBST.
Key takeaway
Forward chaining is also known as forward deduction or forward reasoning when using an inference engine. Forward chaining is a method of reasoning that begins with atomic sentences in a knowledge base and uses inference rules to extract more information in the forward direction until a goal is reached.
Beginning with known facts, the Forward-chaining algorithm activates all rules with satisfied premises and adds their conclusion to the known facts. This procedure is repeated until the problem is resolved.
It's a method of inference that starts with sentences in the knowledge base and generates new conclusions that may then be utilized to construct subsequent inferences. It's a plan based on data. We start with known facts and organize or chain them to get to the query. The ponens modus operandi is used. It begins with the data that is already accessible and then uses inference rules to extract new data until the goal is achieved.
Example: To determine the color of Fritz, a pet who croaks and eats flies, for example. The Knowledge Base contains the following rules:
If X croaks and eats flies — → Then X is a frog.
If X sings — → Then X is a bird.
If X is a frog — → Then X is green.
If x is a bird — -> Then X is blue.
In the KB, croaks and eating insects are found. As a result, we arrive at rule 1, which has an antecedent that matches our facts. The KB is updated to reflect the outcome of rule 1, which is that X is a frog. The KB is reviewed again, and rule 3 is chosen because its antecedent (X is a frog) corresponds to our newly confirmed evidence. The new result is then recorded in the knowledge base (i.e., X is green). As a result, we were able to determine the pet's color based on the fact that it croaks and eats flies.
Properties of forward chaining
● It is a down-up approach since it moves from bottom to top.
● It is a process for reaching a conclusion based on existing facts or data by beginning at the beginning and working one's way to the end.
● Because it helps us to achieve our goal by exploiting current data, forward-chaining is also known as data-driven.
● The forward-chaining methodology is often used in expert systems, such as CLIPS, business, and production rule systems.
Backward chaining
Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.
It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.
Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:
If X croaks and eats flies — → Then X is a frog.
If X sings — → Then X is a bird.
If X is a frog — → Then X is green.
If x is a bird — -> Then X is blue.
The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.
Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.
Properties of backward chaining
● A top-down strategy is what it's called.
● Backward-chaining employs the modus ponens inference rule.
● In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.
● Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.
● The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.
● The backward-chaining method relied heavily on a depth-first search strategy for proof.
Key takeaway
It's a type of inference technique. The following steps are carried out.
1. Analyze data and make logical assertions from it (propositional or predicate logic).
2. Put them in the normal Conjunctive form (CNF).
3. Make an argument in opposition to the conclusion.
4. To locate a solution, use the resolution tree.
For instance: If the jewelry was taken by the maid, the butler was not to blame.
Either the maid took the jewels or she milked the animal.
The butler received the cream if the cow was milked by the maid.
If the butler was at fault, he received his cream as a result.
Step1: Expressing as propositional logic.
P= maid stole the jewellery.
Q= butler is guilty.
R= maid milked the cow.
S= butler got the cream.
Step 2: Convert to propositional logic.
1. P — -> ~Q
2. P v R
3. R — -> S
4. Q — -> S (Conclusion)
Step 3: Converting to CNF.
1. ~P v ~Q
2. P v R
3. ~R v S
4. ~Q v S (Conclusion)
Step 4: Negate the conclusion.
~ (~Q v S) = Q ^ ~S
It is not in CNF due to the presence of ‘^’. Thus, we break it into two parts: Q and ~S. We start with Q and resolve using the resolution tree.
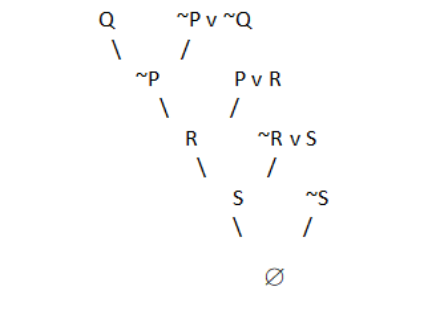
Fig 7: Resolution tree
A null value is obtained by negating the conclusion. As a result, our conclusion has been proven.
References: