Unit - 3

Design of short and long column

3.1 Design of short and long column with axial and eccentric loadings

Axially Loaded Short Columns with Minimum Eccentricity Requirement

Assumptions (Clause 39.1 of IS456: 2000)

(1) The maximum compressive strain in concrete in axial compression is taken as 0.002

(2) Strain in concrete and steel are equal.

(3) The maximum compressive strain at the highly compression extreme fiber in concrete subjected to axial compression and bending and when there is no tension on the section shall be 0.0035 minus 0.75 times the strain at the least compressed extreme fiber.

(4) Stress in steel is governed by characteristic stress-strain curve of steel in compression. The stress-strain curve of steel in compression is the same as in tension.

(5) The column is short.

Equation for Short Axially Loaded Tied Columns (Clause39.3 of IS456: 2000)

According to Clause 39.3 of IS456 2000, when the eccentricity does not exceed 0.05 times the lateral dimension, the member may be designed by the following equation.

P u= 0.4fck Ac+0.67fy.Asc

Where Pu, = factored axial load on the member,

Fck = characteristics compressive strength

Ac = area of concrete

Fy = Characteristics strength of the compression reinforcement

Asc = area of longitudinal reinforcement for column.

Equation of Short Axially Loaded

Columns with Helical Ties (Clause39.4 of IS 456: 2000)

The code further recommends that the ratio of volume of helical reinforcement to the volume of core shall not be less than 0.36 (A/A, -1) (fa/), in order to apply the additional strength factor of 1.05 (Clause 39.4.1). Accordingly, the governing equation of the spiral columns may be written as

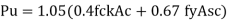
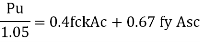
The pitch of helical reinforcement is determined using the following relation as per C1 39.4.1 of IS456 2000.

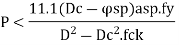
Where Dc = Diameter of concrete core,

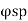= Diameter of spiral reinforcement,

Asp= Area of cross-section of spiral reinforcement,

P= Pitch of spiral reinforcement.

Note: The pitch and diameter of the spiral reinforcement should also satisfy Clause 26.5.3.2 of IS456: 2000.

Design Procedure for Axially Loaded Short Columns

Step 1: Find effective length.

Step 2: Find the minimum eccentricity and check the type of column.

Step 3: Find the area of steel

Use, Pu = 0.4fck Ac+0.67fy, Asc

Step 4: Design of lateral ties

The diameter of transverse reinforcement (lateral ties) is determined from Clause 26.5.3.2 C-2 of IS456 as not less than

(i)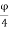 and

(ii) 6 mm.

The pitch of lateral ties, as per Clause26.5.3.2 C-1 of IS456, should be not more than the least of

(i) Sixteen times the smallest diameter of longitudinal reinforcement bar to be tied.

(ii) The least lateral dimension of the column.

(iii) 300 mm

Step 5: Draw the cross section.

Column

Column is a compression member, the effective length exceeds 3 times the least lateral dimension.

Left> 3 x least lateral dimension

Types of Columns (As per Clause 25.1.2 of IS456: 2000) 

Pedestal 

Short column

Long column 

These above types are explained follows,

1)     Pedestal

If the length of column is less than 3 times its least lateral dimension lex/ D <3 or ley / b< 3, it is called a pedestal.

The other horizontal dimension D shall not exceed four times of b

2) Short Column 

If both the slenderness ratios lex / D and ley / b ≤ 12, the column is a short column.

3) Long Column 

If for a column lex/ D and ley/b > 12, it is a slender column in respect of major or minor axis, respectively

If both slenderness ratios are greater than 12, it is slender column in respect of both axes.

Here,

L ex= Effective length of column in respect of the major axis,

D = Depth in respect of the major axis,

L e y = Effective length of column in respect of minor axis, and 

b = Width of the member. 

Strain and stress variation diagrams 

Effective Length (Clause 25.2 of IS456: 2000)

The effective length of a column (effective) is not equal to lo unsupported length (l) in all cases.

Effective length of column for different end conditions (clause 25.2 and table 28 of IS456 – 2000) 

Effective length

1. Effectively held in position and restrained against rotation in both ends – 0.65 l
2. Effectively held in position at both ends, restrained against rotation in one end – 0.80 l
3. Effectively held in position at both ends, but not restrained against rotation – 1.00 l
4. Effectively held in position and restrained against rotation in one end and at other restrained against rotation but not held in position – 1.20 l
5. Effectively held in position and restrained against rotation in one end and at other partially restrained against rotation but not held in position – 1.5 l
6. Effectively held in position at one end but not restrained against rotation and at other end restrained against rotation but not held in position – 2.00 l
7. Effectively held in position and restrained against rotation in one end but not held in position nor restrained against rotation at the other end – 2.00 l

Assumptions

The assumptions for strength style of columns may be summarized as follows.

1. Strain of steel and concrete is proportional to distance from basic axis

2. Most usable compression strain of concrete is zero.

3. Stress, psi, in longitudinal reinforcing bars equals steel strain s times twenty-nine,000,000 for strains below yielding, and equals the steel yield strength ƒy, tension or compression, for larger strains

4. Durability of concrete is negligible.

5. Capability of the concrete in compression that is assumed at a most stress of, should be in line with check results. An oblong stress distribution zero.85ƒc could also be used. Depth of the parallelogram could also be taken as a 1c, wherever c is that the distance from the neutral axis to the acute compression surface and one zero.85 for ƒc 4000 psi and zero.05 less for a thousand psi that ƒc exceeds4000 psi, however one mustn't be taken but zero.65.

Minimum eccentricity

Minimum Eccentricity (Clause 25.4 of IS456: 2000)

It is noted that in practical construction, columns are rarely truly concentric.

Even a theoretical column loaded axially which have the accidental eccentricity due to incorrect accuracy in construction or variation of materials etc.

Accordingly, all axially loaded columns which designed considering the minimum eccentricity which shows in Clause 25.4 of IS456 and given below.

E x min ≥ greater of (+) or 20 mm

E y min ≥ greater of (+) or 20 mm

Where l, D and b are the unsupported length, larger lateral dimension and least lateral dimension, respectively

Maximum Eccentricity (Clause 39.3 of IS456: 2000)

For the column to be short, as per Clause 39.3 the eccentricity shall not be more than 0.O5D or 0.05b.

Short column under axial compression

Assumptions (Clause 39.1 of IS456: (000)

The maximum compressive strain in form of the concrete in axial compression is taken as 0.002.

Strain in concrete and steel are equal.

The maximum compressive strain at the highly compressed extreme fiber which is form in concrete subjected to axial compression and bending and if is no tension on the section which is 0.0035 minus 0.75 times the strain at the least compressed extreme fiber.

Stress in steel is governed by characteristic stress-strain curve of steel in compression. The stress-strain curve of steel in compression is the same as in tension.

The column is short.

Equation for Short axially Loaded Tied Columns (Clause39.3 of IS456: 2000)

According to Clause 39.3 of IS456: 2000, when the eccentricity does not exceed 0.05 times the lateral dimension, the member may be designed by the following equation

P u = 0.4 f c k Ac + 0.67 f y A s c

Where,

Pu = factored axial load on the member,

F c k= characteristic compressive strength where P. Of the concrete,

A c=area of concrete,

F y= characteristic strength of the compression reinforcement, and

A s c= area of longitudinal reinforcement for columns.

Equation of Short Axially Loaded Columns with Helical Ties (Clause39.4 of IS 456: 2000)

The code further recommends that the ratio of volume of helical reinforcement to the volume of core shall not be less than 0.36 (Ag / Ac - 1) (f c k / fy), in order to apply the additional strength factor of 1.05 (Clause 39.4.1).

Accordingly, the governing equation of the spiral columns may be written as

P u = 1.05 (0.4 f c k Ac + 0.67 fy A s c)

= 0.4 f c k Ac + 0.67 fy A s c

The pitch of helical reinforcement is determined using the following relation as per CI 39.4.1 of IS456: 2000.

P <

Where,

Dc = Diameter of concrete core,

D sp = Diameter of spiral reinforcement,

A sp =Area of cross-section of spiral reinforcement,

p= Pitch of spiral reinforcement.

Note:

The pitch and diameter of the spiral reinforcement should also satisfy Clause 26.5.3.2 of 19456: 2000.

Design Procedure for Axially Loaded Short Columns

Step 1: Find effective length.

Step 2: Find the minimum eccentricity and check the type of column.

Step 3: Find the area of steel

Use, P u = 0.4 f c k Ac + 0.67 fy A s c

Step 4: Design of lateral ties

The diameter of transverse reinforcement (lateral ties) determined from Clause 26.5.3.2 C-2 of IS456 as not less a (1) d/2 (2) 6 mm.

Where, d = diameter of bar

The pitch of lateral ties, as per Clause26.5.3.2 C-1 of IS45 should be not more than the least of

The least lateral dimension of the column

Sixteen times the smallest diameter of longitudinal reinforcement bar which can tied.

300 mm

Step 5: Draw the cross section

Problems

Examples 1:

Design an axially loaded column 400 mm x 450mm pined at both ends with a n unsupported length of 3 m for carrying axial service load of 2000 kn Use M20 and Fe415

Solution:

Given:

b = 400mm

D= 450mm

L= 3 m

Fck= 20 N/mm^2

P= 2000 kN

Fy = 415 N/mm^2

To find: Reinforcements

1. Check for minimum eccentricity

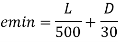
Clauses 25.4 of IS456:2000

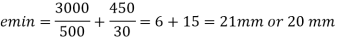
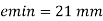
Emin < emax the formula given for axial load is applicable.

2.     Factored load

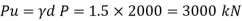
3.     Longitudinal reinforcement

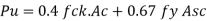
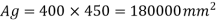
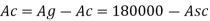
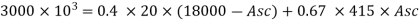
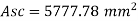
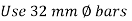
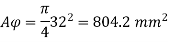
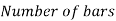
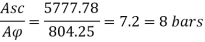
Provide 8-32 mm bars as longitudinal steel

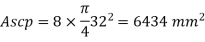
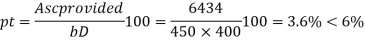
Use cover 40 mm

Steel spacing

Clear spacing between bars = 144-32 = 112 mm < 300 mm        o.k.

4.     Transverse steel

Ref clauses 25.5.3.2 c-2 page no 49 of iS 456-2000

1. Diameter of link or lateral lies < ¼ diameter of largest longitudinal bars
2. Diameter < 6 mm

Whichever is greater

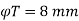
Spacing for lateral ties

1. Least lateral dimension b= 400 mm
2. 16 x diameter of longitudinal bar = 16 x 32 = 512 mm
3. 300mm

Whichever is least

Spacing = 300 mm

Provide lateral ties of 8 mm at 300 mm c/c

Examples 2: Design a square column with the following data:

Factored load = 3000 kN

Concrete grade = M20

Steel = Fe415

Unsupported length of column =3 m

Check for minimum eccentricity

Solution:

Given: Pu = 3000x 10^3 N

Fck = 20 N/mm^2

Fg = 415 N/mm^2

L= 3000 mm

To find:

Size of column and steel reinforcement

Step 1: Size of column

Assume area of steel is 1% of grass area

Asc = 0.01 Ag

Area of concrete = Ag=Asc= Ag (1-0.008) = 0.992 Ag

Factored load Pu= 0.4 fck. Ac +0.67 fy Asc

3000x 10^3 = 0.4 x 20 x 0.992 Ag +0.67 x 415x0.008Ag

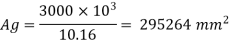
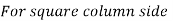
Dimension of column = 560 mm >400 mm

The formula is axially loaded column is applicable

Step 2 Check for minimum eccentricity

1. Emin = L/500 + D/30 = 3000/500 +560/30 = 24.67 mm
2. e min = 20 mm

Whichever is greater

e min = 24.67 mm

e max= 0.05 D = 20 mm

e min < e max     ok

Step 3 Slenderness ratio

Le /D = 3000/560 = 5.36 <12

Step 4 Longitudinal Steel

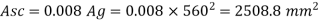
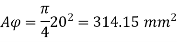
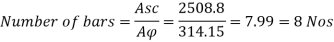
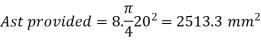
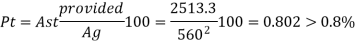
Step 5 Lateral steel

1. Diameter = ¼ 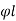or 6 mm

Whichever is greater

= 20/4 or 6 mm

= 5 or 6

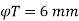
2.     Spacing of ties

1. LLD= 560 mm
2. 16
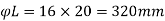
3. 300 mm whichever is less

Provided 6 mm dia. Lateral ties at a spacing 300 mm c/c

Step 6 Reinforcement details

Examples 3 Design a circular column to carry an axial load 1600 KN using concrete M20 and Fe415 steel. The unsupported length of column is 3.75 m.

Solution:

Given:

P = = 1600, fck =20 N/mm^2

Fy = 415 N/mm^2

L= 3750 mm

To find:

Step 1 Factored load Pu

Pu = 1.5 P= 1.5 x 1600=2400 KN

Step 2 Diameter of column

Assume Asc = 0.8% Ag = 0.008Ag

Ac = Ag-Asc= (1-0.008) Ag-0.992Ag

Using equation:

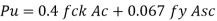
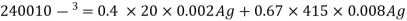
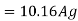
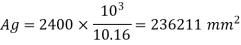
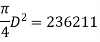
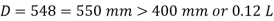
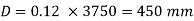
Step 3: Slenderness ratio

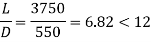
Step 4: Longitudinal reinforcement

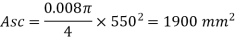
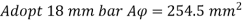
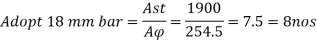
Provide 8-18 mm bar

Step 5 Transverse steel

Diameter of circular ties

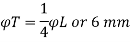
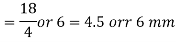
Spacing of circular ties

1. D= 550 mm
2. 16= 288
3. 300 mm

Spacing = 280 mm c/c

Provide circular ties 6 mm at 280 mm c/c

Q.4 Design an axially loaded column 400 mm x 450 mm pinned at both ends with an unsupported length of 3 m for carrying axial service load of 2000 kN. Use M20 Fe415.

Given:

b = 400 mm

D = 450 mm

L = 3m

P = 2000 KN

F c k = 20 N/mm2

F y = 415 N/mm2

To find: Reinforcements

Solution:

Step 1: Check for minimum eccentricity

e min = (+)

=  ( +  )

= 21 mm or 20 mm       …………. Whichever is greater

e min = 21 mm

e max = 0.05 D = 0.05 x 450 = 22.5 mm

e min < e max, the formula given for axial load I applicable

Step 2: Factored load P u = d x p = 1.5 x 2000 = 3000 KN

Step 3: Longitudinal reinforcement:

Pu = 0.4 fck Ac + 0.67 fyAsc

Ag = 450 x 400 = 180000 mm2

Ac = Ag – Asc

= 180000 –Asc

3000 x 103 = 0.4 x 20 x (180000 – As c) + 0.67 x 415 x Asc

= 1.44 x 106 – 8 Asc + 278.05 Asc

270 Asc = 1.56 x 196

Asc = 5777.8 mm2

Using 32 mm diameter of bar

Area of one bar Ad = • d2 = • 322 = 804.2 mm2

Number of bars n = 7.2 = 8 bar

Provide 8 – 32 mm bar as longitudinal steel

A s c provided = 8 x 322 = 6434 mm2

Pt = x 100

= x 100

= 3.6 % < 6 %      ……………………OK

Use cover 40 mm

Steel spacing = 144 mm

Clear spacing between bars = 144 – 32 = 112 mm < 300 mm

Step 4: Transverse steel:

Diameter of link or lateral ties should not less not x diameter of largest longitudinal bar

= x 32 = 8 mm

Diameter should not less not 6 mm

Dt = 8 mm       ……………………. Whichever is greater

Spacing for lateral ties

The least lateral dimension b = 400 mm

16 x diameter of longitudinal reinforcement bar = 16 x 32 = 512 mm

300 mm

Spacing = 300 mm             ……….... Whichever is least

Provided lateral ties of 8 mm diameter of bar at 300 mm c/c

Q.5 Design a square column with the following data Factored load = 3000 k N concrete grade = M20 Steel = Fe415 Unsupported length of column = 3 m Check for minimum eccentricity

Answer

Given:

Pu = 3000 x 103 N

F ck = 20 N/mm2

F y = 415 N/mm

L = 3000 mm

To find: Size of column and steel requirement

Solution:

Step 1: Size of column

Assume area of steel is 1% of grass area

Asc = 0.01 Ag

Area of concrete = Ag – Asc

= Ag (1 – 0.008)

= 0.992 Ag

Factored load, Pu = 0.4 fck Ac + 0.67 fyAsc

3000 x 103 = 0.4 x 20 x 0.992 Ag + 0.67 x 415 x 0.008 Ag

A g = 295264 mm2

For square column side,

= 544 mm = say 560 mm

Dimension of column = 560 m > 400 mm

The formula given for axial load I applicable

Step 2: Check for minimum eccentricity

e min = (+)

=  ( +  )

= 24.67 mm or 20 mm       …………. Whichever is greater

e min= 24.67 mm

e max = 0.05 D = 0.05 x 560 = 28 mm

e min< e max,     ……………………………….OK

Step 3: Slenderness ratio

= 5.36 < 12        ……………………..Short column

Step 4: Longitudinal steel

Asc = 0.008 x Ag = 0.008 x 5602

= 2508.8 mm2

Using 20 mm diameter of bar

Area of one bar Ad = • d2 = • 202 = 314.15 mm2

Number of bars n = 7.99 = 8 bar

Provide 8 – 20 mm bar as longitudinal steel

As c provided = 8 x 202 = 2513.3 mm2

Pt = x 100

= x 100

= 0.802 % > 0.8 %      ……………………OK

Step 5: Transverse steel:

Diameter of link or lateral ties should not less not x diameter of largest longitudinal bar

= x 20 = 5 mm

Diameter should not less not 6 mm

Dt = 6 mm       ……………………..whichever is greater

Spacing for lateral ties

The least lateral dimension b = 560 mm

16 x diameter of longitudinal reinforcement bar = 16 x 20 = 320 mm

300 mm

Spacing = 300 mm             ……….....whichever is least

Provided lateral ties of 6 mm diameter of bar at 300 mm c/c

Step 6: Reinforcement details:

Q.6 Design a circular column to carry an axial load 1600 kN using concrete M 20 and Fe415 steel. The unsupported length of column is 3.75 m.

Answer:

Given:

Pu = 1600 x 103 N

F ck = 20 N/mm2

F y = 415 N/mm

L = 3750 mm

To find: Diameter of column and steel requirement

Solution:

Step 1: Factored load Pu = 1.5 P = 1.5 x 1600 = 2400 KN

Step 2: Diameter of column

Assume area of steel is 1% of grass area

Asc = 0.01 Ag

Area of concrete = Ag – Asc

= Ag (1 – 0.008)

= 0.992 Ag

Using equation,

Pu = 0.4 fck Ac + 0.67 fyAsc

2400 x 103 = 0.4 x 20 x 0.992 Ag + 0.67 x 415 x 0.008 Ag

Ag = 236211 mm2

D = 548 = 550 mm > 400 mm

Or 0.12 x L = 0.12 x 3750 = 450 mm

Step 3: Slenderness ratio

= 6.82< 12        ……………………..Short column

Step 4: Longitudinal steel

Asc = 0.008 x Ag = 0.008 x 5502

= 1900 mm2

Using 18 mm diameter of bar

Area of one bar Ad = • d2 = • 182 = 254.5 mm2

Number of bars n = 7.5 = 8 bar

Provide 8 – 18 mm bar as longitudinal steel

Step 5: Transverse steel:

Diameter of link or lateral ties should not less not x diameter of largest longitudinal bar

= x 18 = 4.5 mm

Diameter should not less not 6 mm

Dt = 6 mm       ……………………..whichever is greater

Spacing for lateral ties

The least lateral dimension D = 550 mm

16 x diameter of longitudinal reinforcement bar = 16 x 18 = 288 mm

300 mm

Spacing = 288 mm = 280mm           ….....whichever is least

Provided lateral ties of 6 mm diameter of bar at 280 mm c/c

Step 6: Reinforcement details:

Short Compression Members under Axial Load with Biaxial Bending

Beams and girders transfer their end moments near the corner columns of a building frame in two perpendicular planes. Interior columns have biaxial moments if the layout of the columns is irregular. Accordingly, such columns are design considering axial load with biaxial bending.

Requirements for reinforcement

Types of Column Reinforcement

A column has two types of reinforcements as mention as below,

• Longitudinal or main reinforcement 
• Transverse or lateral reinforcement 
• Helical reinforcement 

Longitudinal or Main Reinforcement (Clause 26.5.3.1 of IS456: 2000)

The longitudinal reinforcement resists axial load and bending moment.

The transverse reinforcement resists shear force, shares a small fraction of axial load if provided in the form of helical reinforcement, keeps main reinforcement in position and prevents longitudinal bars from buckling.

The longitudinal reinforcing bars in the form of vertical steel are used to carry the compressive loads along with the concrete. The following are the IS requirement for design of column:

IS requirement for design of column

1. Areas of longitudinal steel 
2. Minimum number of longitudinal steel 
3. Diameter of longitudinal steel 
4. Spacing of longitudinal bars
5. Nominal cover to longitudinal bars 

(A) Areas of longitudinal steel 

Minimum amount of steel should not be less than 0.80 % of gross cross-sectional area 

Amount of area should not be more than 4 % of the gross cross-sectional area of the column

In no case, it does not exceed 6 % when bars from column below have to be lapped with those in the column under consideration. 

(B) Minimum Number of longitudinal steel

For rectangular column shall be 4

For circular columns shall be 6 

(C) Diameter of longitudinal steel

The diameter of the longitudinal bars shall not be less than 12 mm

(D) Spacing of longitudinal bars 

The minimum horizontal spacing between two parallel main bars shall not be less than diameter of larger bar or maximum size of coarse aggregate plus 5 mm.

The maximum spacing of longitudinal bars measured along the periphery of the column shall not be more than 300 mm. 

(E) Nominal cover to longitudinal bars

Nominal cover in case of a column equals to (i) 40 mm (ii) the diameter of longitudinal bar whichever is greater. 

In case of columns of width 200 mm or less whose longitudinal bar not exceed 12 mm diameter, the nominal cover of 25mm may be used.

Transverse or Lateral Reinforcement (Clause 26.5.3.2 of IS456: 2000) 

Clause 26.5.3.2(b) of IS 456: 2000 stipulates the guidelines of the arrangement of transverse reinforcement as under. 

As per Clause 26.5.3.2 (b)(1), If the longitudinal bars are not spaced more than 75 mm on either side, transverse reinforcement shall only go round corner and alternate bars for the purpose of providing effective lateral supports. 

As per Clause 26.5.3.2 (b)(2), If longitudinal bars spaced at a distance not exceeding 48 times the diameter of the tie are effectively tied in two directions, additional open ties are provided in between longitudinal bars 

As per Clause 26.5.3.2(b)(3), For longitudinal bars in compression members are placed in more than one row 

As per Clause 26.5.3.2(b) (3(i), Transverse reinforcement is provided for the outer-most row in accordance with (a) above, and

As per Clause 26.5.3.2 (b)(3(ii), no bar of the inner row is closer to the nearest compression face than three times the diameter of the largest bar in the inner row.

The diameter of such transverse reinforcement need not, however, exceed 20 mm

Pitch and Diameter of Lateral Ties (Clause 26.5.3.2(c) of IS456: 2000) 

1) Pitch 

The pitch of transverse reinforcement shall be the least of the following,

The least lateral dimension of the compression 9.5 members 

Sixteen times the smallest diameter of the longitudinal reinforcement bar to be tied; and 

300 mm.

2) Diameter

The diameter of the polygonal links or lateral ties is not less than one-fourth of the diameter of the largest longitudinal bar, and in have no case less than 6 mm.

Column with helical reinforcement

Helical Reinforcement (Clause 26.5.3.2 (d) of IS456: 2000) 

1)     Pitch

Helical reinforcement which the regular formation with the turns of the helix spaced having evenly and its ends anchored properly by providing one and a half extra turns of the spiral bar.

The pitch of the helical turns shall not be the more than 75 mm, nor more than one sixth or the core diameter of the column, not less than 25 mm or less than three times the diameter of the steel bar forming the helix

2)     Diameter

The diameter of the helical reinforcement shall be as mentioned

Interaction Diagrams

The interaction diagram is the curve drawn with (as an abscissa and) ordinate for the various values of p ranging from 0 to 0.26 for distribution of reinforcement such as equal reinforcement on two parallel faces or on all faces of rectangular sections.

This diagram is also called as Pu – Mu interaction curve.

This diagram is drawn for square, rectangular and circular column for different grades of concrete and steel.

This diagram is advantageously used for the column subjected to axial load and bending moment. This diagram provides for the different modes of failures namely compression failure, balanced failure and tension failure.

The interaction curve is drawn for various load-moment (Pu and Mu) combinations for all possible eccentricities of loading. For design purposes, Pu and Mu are calculated on the basis of design stress-strain curves (including partial safety factors).

The design interaction curve represents the failure envelope and the point given by the co-ordinates (Pu and Mu) falling within the interaction curve indicates the safe values of the combination of load and moments.

The salient points on the interaction curve are as under.

Point-1 corresponds to the axial loading with zero moment (P u) and e = 0. This indicates, the column is subjected to axial load only.

Point-1' corresponds to the axial load with the minimum eccentricity prescribed in Clause 254 of 5456 the corresponding ultimate load is represented as P u

As the eccentricity increases, the moment increases with the neutral axis xu moving from outside towards the extreme fiber.

Point-3 on the interaction diagram indicates the balanced failure state. The design strength values for the balanced failure condition are denoted as Pub and Mub

Point-4 on the interaction curve refers to the pure flexural state (Pu= 0) with the ultimate moment of resistance Muo 

Interaction diagrams or Design Charts of SP-16

SP-16 has three sets of design charts prepared by IS456 published in SP-16 for rectangular and circular types of cross- sections of columns. These three sets are as follows:

The charts 27 to 38 are the first set of twelve charts for rectangular columns having symmetrical longitudinal steel bars in two rows for three grades of steel (Fe250, Fe415 and Fe500) and each of them has four values of d'/D ratios (0.05, 0.10, 0.15 and 0.20).

Charts 39 to 50 are the 2nd set of 12 charts for rectangular columns which have the symmetrical longitudinal steel bars (twenty numbers) distributed equally on four sides (in six rows, for three grades of steel (Fe250, Fe415 and Fe500) and each of them having four values of d/D ratios (0.05, 0.10, 0.15 and 0.20).

The 3rd set of 12 charts have the numbering from 51 to 62, are for circular columns having eight longitudinal steel bar equal diameter and uniformly spaced circumferentially for three grades of steel (Fe250, Fe415 a Fe500) and each of them haves four values of d'/D ratios (00s 0.10,0.15 and 0.20).

All the 36 charts which can prepared for M 20 grade of concrete only.

Chart 1: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on opposite sides

Chart 2: Interaction diagram for combined bending and compression rectangular section- equal reinforcement on opposite sides 

Chart 3: Interaction diagram for combined bending and compression rectangular section- equal reinforcement on opposite sides 

Chart 4: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on opposite sides

Chart 5: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on all sides

Chart 6: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on all sides

Chart 7: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on all sides 

Chart 8: Interaction diagram for combined bending and compression rectangular section-equal reinforcement on all sides 

Approximations and Limitations of Design Charts of SP-16 9.14.2.1

Approximations

The following are the approximations of the design charts of SP-16:   

(a) Grade of concrete

(b) The d'/D ratio

(c) Equal distribution of twenty longitudinal steel bars on four sides of rectangular columns

(d) Longitudinal bars in circular columns 

This are approximations are explained s follow

Grade of concrete

As mentioned in earlier section, all the design chars of SP-16 assume the constant grade M 20 of concrete.

However, each chart has fourteen plots having different values of the parameter p/f ranging from zero to 0.26 at an interval of 0.02. The designer which can formed to be use of the actual grade of concrete by multiplying the p/fck which can obtain from the plot with the actual fck for the particular grade of concrete to partially compensate the approximation.

The d'/D ratio

The three sets of charts have four fixed values of d'/D ratios (0.05, 0.10, 0.15 and 0.20). However, in the practical design, the d'/D ratio may be different from those values. In such situations intermediate values are determined by making linear interpolations.

Equal distribution of 20 longitudinal steel bars on four sides of rectangular columns

In above consideration, the design charts can used without significant error for any number of bars greater than eight provided the bars which can be distributed equally on four sides.

Longitudinal bars in circular columns

Though the design charts are prepared considering eight bars uniformly placed circumferentially, they may generally be used for any number of bars greater than six, uniformly placed circumferentially.

Limitations

Limitations of the design chars of SP-16 are as follow

Longitudinal bars equally distributed on four sides of rectangular columns

Unsymmetrical arrangement of longitudinal bars in rectangular cross-sections non-uniform placing of longitudinal bars in circular cross-sections

Cross-sections other than rectangular or circular like, I, T, H, X etc.

Concluding remarks 

Short column under axial load and uni-axial bending

It is known that the design of columns by direct computations involves several trials for exact determination of steel percentage in which the percentage is assumed by comparing the strength calculated from the assumed steel with the given load on the column and hence, time taking. Thus, design charts prepared by IS456 published in SP-16 are used in getting several alternative solutions quickly.

Further, these design charts are also used for the analysis of columns for safety etc.

However, there are limitations of using the design charts, which are mentioned in the succeeding sections.

The Analysis of Short Columns under Axial Load with Uniaxial Bending

In many situations, it becomes necessary to assess the safety of a column with known cross-section dimensions, and longitudinal and transverse steel reinforcing bars. The objective is examined if the column can resist some critical values of Pu or Mu or pairs of Pu and Mu as may be expected to be applied on the column.

This is done by comparing if the given values of pair of Pu and Mu Pu and Mu are less than the respective strength capacities pair of Pu and Mu.

The word "given" shall be used in the suffix of pairs of Pu and Muto indicate that they are the given values for which the column has to be examined. The strength capacity of the column, either Pu or Mu alone or pair of Pu and Mu will not have any suffix. Thus, the designer shall assess

(Pair of Pu and Mu) given< Pair of P u and Mu, as strength capacities

This type of problem is known as analysis types of problem the three steps are given below are used to design the column using design charts of SP-16.

Step 1: Select the respective design chart,

Specified by the chart number, from the known value of d'/D and the grade of steel for circular columns; and considered the distribution of longitudinal steel bars equally on two or four sides for the rectangular columns.

Step 2: Select the particular curve

Select the particular curve out of the family of 14 curves in the chart selected in Step 1. The selection of the curve shall be made from the value of p/fck parameter which is known.

Step 3: Assessment of the column

This can be done in any of the three methods selecting two of the three parameters as known and comparing the third parameter to satisfy. The parameters are Pu /fckbD. Mu/fckbD2and p/fck for rectangular columns. For circular columns the breadth b shall be replaced by D (the diameter of the column).

Design of Short Columns under Axial Load with Uniaxial Bending

The design of columns involves with the determination of percentage of longitudinal steel p, assuming or knowing the dimensions b and D, grades of concrete and steel, distribution of longitudinal bars in two or multiple rows and d'/D from the analysis or elsewhere. This can be minimized by using the design charts prepared by IS456 in SP-16.

The procedure to design the column using design charts of SP-16 is explained below:

Step 1: Assume the size of the column

Assume the size of the column and calculate d'/D.

Step 2: Calculate P u / f c k b D and M u / f c k b D2

Step 3: Selection of the design chart

Select suitable the design chart from SP-16 for the corresponding to d'/D, grade of concrete and distribution of steel.

Step 4: Determination of the percentage of longitudinal steel

Locate the point of intersection of P u /f c k b D and M u / f c k b D2 and find the suitable value of p/fck

Thus, amount of longitudinal steel is obtained by using the following relation.

Asc = p b D /100 fck

Step 5: Design of transverse reinforcement

Design the transverse ties as per the section 9.3.2.1,

Design of columns under bi-axial loading by Design Charts

IS Code Method for Design or Columns under Axial Load and Biaxial Bending (Clause 39.6 of IS456: 2000)

A Clause 39.6 of IS456 recommends the following Simplified formula, based on "Breslers load Contour Method", for the of biaxial loaded columns. The relationship between Muxx and Muyz for a particular value of Pu = Puz expressed dimensional form is

(M u x / Mu x 1) + (M u y / M u y 1) ≤ 1

Where,

Mux and Muy= moment about x and y axes due to design load

Mux1and Mu y 1= maximum uniaxial moments the column can take under the actual load P by bending about x and y axes.

n is related to Pu, /Puz where

Puz= design load on the column

Puz= 0.45 fck Ac + 0.75 fyAsc (I e value Pu of when M = 0)

Puz= 0.45 fc k Ag (0.75 fy – 0.45 fck) Asc

n = Exponent whose value is to be taken as follow:

Where,

Ag= gross area of the section, and

Asc = total area of steel in the section

It is worth mentioning that the quantities Mux, Muy and Pu are due to external loadings applied on the structure and are available from the analysis

Whereas Mux, Muy and Pu are the capacities of the column section to be considered for the design.

Solution of Problems using IS Code Method

18456: 2000, suggest the following steps to design the columns subjected to load and biaxial moment.

1)     Selection of trial section for the design type of problems

The preliminary dimensions are assumed during the analysis of structure Assume the percentage of longitudinal steel from the given Mux, Muy, Pu, fy and fck

Note:

Pillai and Menon suggested a simple way of considering a moment of approximately 15 per cent in excess (lower percentage up to 5 per cent if Pu/Puz is relatively high) of the resultant moment

Mu = 1.15 x (M u x 2 + M u y 2)

As the uniaxial moment for the trial section with respect to the major principal axis xx, if Mu x≥ Muy otherwise, it should be with respect to the minor principal axis.

The reinforcement should be assumed to be distributed equally on four sides of the section.

2)     Checking the eccentricities ex and ey for the minimum eccentricities

Clause 25.4 of IS256 stipulates the amounts of the minimum eccentricities and are given in Equation as follows,

(M u x /M u x 1) + (M u y /M u y 1) ≤ 1

Puz= 0.45 fck Ag +( 0.75 fy – 0.45 fck) Asc

Where 1, b and D are the unsupported length, least lateral dimension and larger lateral dimension, respectively. The clause further stipulates that for the biaxial bending, it is sufficient to ensure that the eccentricity exceeding the minimum value about one axis at a time.

3)     Verification of eccentricities

It is to be done determining ex = Mux/Pu and ey = Muy/Pu from the given data of Mu x, Muy and Pu and Equation above from the assumed b and D and given leff.

4)     Assuming a trial section including longitudinal reinforcement

This step is needed only for the design type of problem, which is to be done as explained in (a) above.

5)     Determination of Mux1 and Muy1

Use of design charts should be made for this. Mux1 and Muy1 corresponding to the given Pu should be significantly greater than Mux and Muy respectively. 

6)     Determination of Puz and n

The values of Puz and n can be determined from Equations as

Puz= 0.45 fck Ag + (0.75 fy – 0.45 fck)

Alternatively, Puz can be obtained from Chart 63 of SP-16.

7)     Checking the adequacy of the section

This is done either using Equation or using Chart 64 of SP-16.

Design of isolated column footing for axial load and uniaxial bending.

Key takeaways:

Design steps

1)     Selection of trial section for the design type of problems

2)     Checking the eccentricities ex and ey for the minimum eccentricities

3)     Verification of eccentricities

4)     Assuming a trial section including longitudinal reinforcement

5)     Determination of Mux1 and Muy1

6)     Determination of P u z and n

7)     Checking the adequacy of the section

Problems:

1) Design a uniaxial square, short column by limit state method with material M 25 and Fe 415 to carry ultimate load of 800 kN and working moment of 80 k Nm about major axis bisecting the depth of column. The unsupported length of column is 3.6m. The column is fixed at one end and hinged at the other. Also design the footing for this column only for flexure and punching shear. Take SBC = 250 kN/m2. Show detailed design calculations and reinforcement details in plan and sectional elevation

Answer: 

Given: Uniaxial square column

M 25, fck = 25 N/mm2

Fe 415 fy= 415 N/mm2

Ultimate load P = 800 kN

Working Moment M = 80 k Nm

Unsupported length L = 3.6 m

End condition: One end fixed and other hinged

Solution

A)    Design of uniaxial square column

Factored Load Pu = 1.5 x P = 1.5 x 800 = 1200 kN

Mu = 1.5 x M = 1.5 x 80 = 120 k N m

Effective length for column Le = 0.8 L = 0.8 x 3600 = 2880 mm

Min. Size of short square column

L e / L L D1 ≤ 12

2880 / b ≤ 12

b > 240 mm

D = 400 mm

Eccentricity

Mu = P u x e

12 x 106 = 1200 x 103 e

e = 100m

e min = unsupported length/500 + lateral dimension /30

= 360/500 + 400/30

= 20.53 mm or 20 mm

e min = 20.5 mm

e > e min, the short column is designed for uniaxial bending.

Determine d/D

Assume cover 60 mm, d/D =50 /400 = 0.15

Percentage of steel from design chart (refer sp – 16, chart 32)

Refer design chart for fy= 415 N/mm2 and d/D = 0.15

P u /f c k b D = 120 * 103 /25 * 400 *400 = 0.3

M u /f c k b D2= 120 * 106 /25 * 400 * 4002 = 0.075

From chart, (refer chart 2)

P u/ f c k = 0.03

P = 0.03 fck = 0.03 x 25 = 0.75 %

Required percentage of steel is less than minimum percentage of steel as per IS 456 i.e., 0.8 %

Interaction Diagram for Combined Bending and Compression Rectangular Section-Equal Reinforcement on All sides.

Area of steel in compression

Asc = p b D /100 = 1 * 400 * 400 = 1600 mm2

Provided 4 bars of 20 mm and 4 bars of 16 mm

As c provided = 4 * π/2 * 202 + 4 * π/2 * 162 = 2061 mm2> 1600 mm2

Design of lateral ties:

Diameter of link or lateral ties should not less not ¼ x diameter of largest longitudinal bar

= ¼ x 20 = 5 mm

Diameter should not less not 6 mm

Dt = 6 mm       ……………………. Whichever is greater

Spacing for lateral ties

The least lateral dimension b = 400 mm

16 x diameter of longitudinal reinforcement bar = 16 x 20 = 320 mm

300 mm

Spacing = 300 mm             ……….... Whichever is least

Provided lateral ties of 6 mm diameter of bar at 300 mm c/c

Design of footing

Assume self wt. Of footing = 10% of load on column

Total load on footing = 1.1 p = 1.1 x 800 = 880kN

Area of footing = total weight on footing /safe bearing capacity of soil

= P u /200 = 880/ 200

= 3.52 m2

Size of footing

Assume square footing L = B = 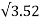= 1.879 = 2 m

Provided size of footing = 2 m x 2 m

Since the column is subjected to eccentricity of 100mm, the C.G. Of footing is taken at 100 mm away from the axis column as shown in fig as below,

Upward soil pressure = load on column /size of footing provided

= 800 /2 *2

= 200 KN/m2< SBC

Depth of footing based on BM:

Critical section for maximum bending moment occurs at the face of column Projection beyond face of column

a = (B-d /2) + e = (2000 – 400/2) + 100

= 900 mm

Bending at face of column

BM = po B a2 /2 = 200 * 2 * 0.92/2 = 162 K Nm

Factored BM,

Mu = 1.5 x M = 1.5 x 162 = 243 K Nm

For Fe415

Mu.lim = 0.138fck bd2

243 x 106= 0.138x 25 x 1000 x d2

d = 265.4 mm

Depth of footing based on punching shear:

Critical section for two-way shear or punching shear is considered at a distance d/2 from the column face periphery.

Share width at critical Section b0 = b+ d = (0.4 + d)

Factored shear force

Vu= 1.5 p o (B2 - b02)

= 1.5 x 200 (22 - (0.4 + d2)

= 300 (4 – (0.16 + 0.8 d + d2)

= 300 (3.84 + 0.8d + d2)       ……… (1)

Shear capacity of concrete,

Vu = v (4 bo do)

But, v= Ks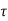c = 1 x 0.25 = 1.25 N/mm2

= 1250 KN/m2

= 500 (0.4 + d) d

= 500 (0.4d + d2)                  …………..(2)

Equating equation (1) and (2), we get,

300 (3.84 +0.8d + d2) = 500 (0.4d + d2)

3.84 +0.8 d + d2 = 16.67 (0.4d + d2)

3.84 +0.8d + d2 = 6.67d+ 16.67 d2

15.67d2 + 5.87 d - 3.84 = 0

Solving quadratic equation by using calculator,

d = 0.342 mm = 0.35 mm.

Assume cover to footing 0.5 m

Overall depth D = d +c = 0.35 + 0.5 = 0.4 m = 400 mm

Provide Depth for footing is 400 mm, which is greater value based on BM and punching shear.

Steel reinforcement

A s t = 0.5 f c k /f y (1 -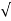1 – ((4.6 M u)/ (f c k b d2) b d

As t = 2020.8 mm2

Using 12 mm diameter of bar

Area of one bar Ad = • d2 = • 122 = 113.09 mm2

Number of bars n = A s t/ A d = 2020.8/ 113.09 = 17.9 = 18 bar

Provide 18 - 12 mm dia. Of bars at an equal distance

Check for development length:

Ld = 47 x d = 47 x12 = 564 mm

2) Design a bi-axial rectangular short column by limit state method with material M25 and Fe 415 to carry a working load of 900 kN. Working moment of 90 kN-m about major axis bisecting the depth of column and 35 kN-m about minor axis bisecting the width of column. The unsupported length of column about major and minor axis is 3.6 m and 3.2 m. The column is fixed at one end and hinged at the other. Show detailed design calculations and reinforcement details.

Answer: 

Given:

Working load = 900 kN

Lex= 3.6 m, fck = 25 N/mm2

Ley = 3.2 m, fy = 415 N/mm2

Solution

Minimum eccentricities

Assume b = 300 mm, D = 500

Ex min = greater of (3600/500+ 300/30) and 20 mm

= 17.2 mm and 20 mm

E y min = greater of (3200/500 +500/30) and 20 mm

= 23.06 mm and 20 mm

P u = ultimate load= 900 x 1.5= 1350 kN

Mux = ultimate moment @ major axes

2x90 = 180 kN-m

Muy= ultimate moment @major axes

2x35 = 70KN-m

E x = M u x/ P u = 133.33

E y = M u y/ P u = 25.93

Ex and ey are greater than ex min and ey min

2) Assuming trial section,

b = 300 mm, d = 500 mm

Mu = 1.15 (mu x2 + muy2) ½

= 1.15 (1802 + 702) ½

=222.10 K Nm

P u /f c k b D=1350 * 103 /25 *300 *500 = 0.36

M u/ f c k b D2= 222.10 * 106 /25 * 300 * 5002 = 0.12

d /D =50/ 500 = 0.1

= 0.08

P = 0.08fck = 0.08 x 25 = 2 %

Area of steel in compression

Asc =p b D/ 100 = 2 * 300 *500 /100 = 3000 mm2

Use 20 mm diameter of bar

Number of bar = 3000/ π/2 202 = 7.55 = 8

Provided 8 bar of 20 mm diameter of bar

Asc provided = = 8 x π/2 x 202 = 2513.3 mm2< 3000 mm2

Pt % (provided) =100 * 2513.3 /300* 500 = 1.68 %

3) Determine of Mux 1 and Muy 1

P u / f c k b D =1350 * 103 /25 * 300 * 500 = 0.36

p/ f c k = 1.68/25 = 0.0672

Determine,

M u /f c k b D2= 222.10 * 10 6/ 25 * 300 * 500 2= 0.12

Mux 1 = 0.11 x 25 x 300 x 5002

= 206.25 x 106 N mm > 180 N mm

P u /f c k b D = 0.36 and   = 0.0672

d/b = 50 / 300 = 0.166

Determine value Muy1/ f c k b D2

d/b = 0.15 and d/b =0.2

For d/b = 0.15 = 0.11

For d/b = 0.2 = 0.09

For d/b = 0.166

Mu y 1/f c k b D2= 0.09 +((0.11 – 0.09)/ (0.2 – 0.15)) x (0.2 – 0.166) = 0.104

Muy1 = 0.104 x 25 x 3002 x 500

= 117 x 106KN m =117 KN m

As Mux1 and Muy1 are significantly greater than Mux and Muy respective. Redesign of section is not needed.

4) Determine P u z

Puz= 0.45 fck Ag +( 0.75 fy – 0.45 fck) Asc

= 0.45 x 25 x 300 x 500 + (0.75 x 415 -0.45 x 25) x 2513.3

= 2441.49 x 103 N

Puz = 2441.49 KN

5) Check for adequacy of section

(M u x/ Mu x 1) + (M u y/ Muy1) ≤ 1

0.88 ≤ 1

Design is safe

Spacing for lateral ties

The least lateral dimension b = 300 mm

16 x diameter of longitudinal reinforcement bar = 16 x 20 = 320 mm

300 mm

Spacing = 300 mm             ……….... Whichever is least

Provided lateral ties of 8 mm diameter of bar at 300 mm c/c

Design of footing

Load of column = 900 KN

Assume self wt. Of footing = 10% of load on column = 90 KN

Total load on footing = 900 + 90 = 990kN

Factored load = 1.5 x 990 = 1485 KN

Area of footing = factored load on footing/ ultimate bearing capacity of soil

= P u/200 = 1485 / 200 *2

= 3.71m2

Size of footing

Assume square footing L = B =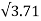= 1.93 = 2 m

Provided size of footing = 2 m x 2 m

Upward soil pressure = load on column /size of footing provided

= 1.5 * 900/ 2* 2

= 337.5 KN/m2

Depth for BM

Determine eccentricity = e =M u/P u = 180/ (1.5 * 900) = 0.023 m = 23 mm

a1 = (L-b)/2 + e

= (2- 0.3)/2 + 0.023

= 0.873 m

a1 = (L-b)/2 - e

= (2- 0.3)/2 - 0.023

= 0.827 m

b1 = (B- a)/2

= (2- 0.5)/2

= 0.75 m

BM calculation

For BM calculation takes greater of a1 and a2

Mxd = Pu calx a12/2 = upward soil pressure a12/2

= 337.5 x 0.8732= 128.60 KN .m

Myd = Pu calx b12/2 = upward soil pressure b12/2

= 337.5 x 0.752/2 = 95 KN .m

Md= maximum of Mxd and My d= 128.60 KN m

For Fe415

Mu.lim = 0.138fck bd2

128.60 x 106= 0.138x 25 x 1000 x d2

d = 193.06 mm

v = should be less than ks 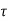c

K s = 0.5 + 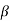c = 0.5 +b/ D = 0.5 +300/ 500 = 1.1

c = 0.25 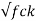= 0.25 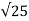= 1.25 N/mm2

v = 1.1x 1.25 = 1.375 N/mm2

Nominal shear stress 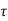v = 1375KN/m2

Vu   = 2 [((2- 0.3)/ 2) – d] x 337.5                 ………1

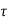v < ks 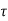c

Shear resisted by concrete

Vu = 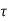c B d

= 1375 x 2 x d

= 2750 d                                            ……2

From equation 1 and equation 2

2 [ ((2- 0.3)/2) – d] x 337.5 =   2750 d 

573.75 – 675d = 2750d

d = 0.168m = 168 mm

Depth is safe against one way shear

Check for two-way shear

Shear force on shaded area

Vu = [22 – (0.3 + d) (0.5 +d)] x 337.5…………Equation 1

Shear force resisted by concrete

Vu = 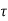c b0 d

b0 = perimeter of critical section

b0 = 2 [(D + d) + (b + d)]

= 2 [(0.3 + d) + (0.5 + d)]

= 2[0.8 + 2d]

= 1.6 + 4d

Vu = b0 d

= 1375 (1.6 + 4d) d …………………Equation 2

Equating Equation (1) and (2)

[22 – (0.3 + d) (0.5 +d)]x 337.5= 1375 (1.6 + 4d) d

3.85 – 0.8 d – d2= 4.07 (1.6d + 4d2)

15.3 d2 + 7.31 d – 3.85 = 0

d = 0.316 = 0.316 m

= 320 mm

Overall depth = D = d + c + d/2

= 320 + 50 + 16/2

= 378 mm = 390 mm

Main reinforcement

A s t = 0.5 f c k /f y (1 -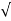1 – ((4.6 M u)/ (f c k b d2) b d

As t = 1357.38 mm2

As t for 2 m width = 2 x 1357.38 = 2714.77 mm2

Using 16 mm diameter of bar

Area of one bar Ad = π/2• d2 = π/2• 162 = 201.01 mm2

Number of bars n =A s t/ A d = 92714.77/ 201.01 = 13.5 = 14 bar

Provided 14 bars of 16 mm diameter of bars

3.2 Design of isolated and combined column footings

Design steps

The following are the steps as how the footing design is being proceeded-

1. Proportion of footing for column

2. Check for bending moment

3. Check for one-way shear

4. Check for two-way shear

5. Check for bearing stress

6. Check for development length

Isolated Column Footings

Used for single column. It may be square, circular or rectangular. The footing is of R.C.C with reinforcement at bottom. Column footing on piles should have a minimum thickness of 30 cm

Thickness of Footing Base Slab

The thickness of a footing base slab is generally based on considerations of shear and flexure, which are critical near the column location.

Generally, shear considerations predominate, and the thickness is based on shear criteria.

Except in the case of small footings, it is economical to vary the thickness from a minimum at the edge to a maximum near the face of the column, in keeping with the variations in bending moment and shear force. This may be achieved either by sloping the top face of the base slab or by providing a stepped footing.

In any case, the IS456 2000 Code (Clause 34.1.2) restricts the minimum thickness at the edge of the footing to 150 mm for footings in general (and to 300 mm in the case of pile caps). This is done to ensure that the footing has sufficient rigidity to provide the calculated bearing pressures.

A 'leveling course of lean concrete (about 100 mm thick) is usually provided below the footing base

Design Considerations

(a) Minimum nominal cover (Clause 26.4.2.2 of IS456)

The minimum nominal cover for the footings should be more than that of other structural elements of the superstructure as the footings are in direct contact with the soil

Clause 26.4.2.2 of IS 456 prescribes a minimum cover of 50 mm for footings

The actual cover may be even more depending on the presence of harmful chemicals or minerals, water table etc.

(b) Thickness at the edge of footings

(Clause 34.1.2 and 34.1.3 of IS 456)

The minimum thickness at the edge of reinforced and plain concrete footings shall be at least 150 mm for footings on soils and at least 300 mm above the top of piles for footings on piles, as per the stipulation in Clause 34.1.2 of 15456.

For plain concrete pedestals. The angle a (see Fig. 9.12.1) between the plane passing through the bottom edge of the pedestal and the corresponding junction edge of the column with pedestal and the horizontal plane shall be determined from the following expression. (Clause 34.1.3 of 15456)

Tan a ≤ 0.90((100q, /) +1)

Where,

Qa, calculated maximum bearing pressure at the base of pedestal in N/mm², and

Fck = characteristic strength of concrete at 28 days

(c) Bending moments (Clause 34.2 of IS 456)

The critical section of maximum bending moment for the purpose of designing an isolated concrete footing which supports a column, pedestal or wall shall be:

(1) At the face of the column, pedestal or wall for footing supporting a concrete column, pedestal or reinforced concrete wall, and

(ii) Halfway between the centre-line and the edge of the wall, for footing under masonry wall. This is stipulated in Clause 34.2.3.2 of 15456.

(d) Shear force (Clause 31.6 and 34.2.4 of IS456)

Footing slabs shall be checked in one-way or two-way shears depending on the nature of bending. If the slab bends primarily in one-way, the footing slab shall be checked in one-way vertical shear. On the other hand, when the bending is primarily two-way, the footing slab shall be checked in two-way shear or punching shear

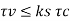
Where k, = 0.5 +Bc

Bc Short side of column /Long side of column

The respective critical sections and design shear strengths are given below

1. One-way shear (Clause 34.2.4 of IS456)

One-way shear has to be checked across the full width of the base slab on a vertical section located from the face of the column, pedestal or wall at a distance equal to effective depth of the footing slab in case of footing slab on soil, and the design shear strength of concrete without shear reinforcement is given in Table 19 of Clause 40.2 of 1S456 or Table 6.6.1

Critical section for shear is assumed as a vertical section located from the face of column at a distance equal to

Where d = effective depth of footing

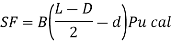
2. Two-way or punching shear (Clause31.6 and 34.2.4)

Two-way or punching shear shall be checked around the column on a perimeter half the effective depth of the footing slab away from the face of the column or pedestal. Normally, the thickness of the base slab is governed by shear. Hence, the necessary thickness of the slab has to be provided to avoid shear reinforcement.

S.F. On shaded area= [LB-(d+D) (b+d)] Pu, cal

Design Procedure for Axially Loaded Isolated Square Footing

Design steps

1. Size of footing

Working load on column= P

Assume weight of footing 5 to 10% of P

Ultimate bearing capacity of soil Pa= 2x Safe B.C. Of soil

Factored load=1.5 (P+ Weight of footing)

Area of footing Af

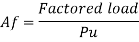
For square shape of footing

Each side (L=B) =

For rectangular footing

Assume L=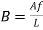

2.     Find upward soil pressure

Neglecting the self-weight of footing

Upwards soil pressure = Factored load on column/Af

3.     Depth of footing for shear

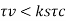
Where

Ks= 0.5 +bc

But ks< 1

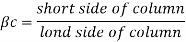
The shear force shall be calculated for two conditions

1. Footing acting as a wide beam
2. Two-way action punching shear

Find effective depth required for both the above condition and provide grather of the two

The critical section for both the cases is considered as follows:

1. Footing acting as a wide beam

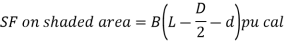
Whichever is greater

SF resisted by concrete Vu =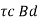

S F on shaded area = SF resisted by concrete

Find depth d

2.     The two ways section – punching shear

The critical section for shear (punching shear) is assumed at a distance d/2 from the periphery of the column

Where d = Effective depth of footing

SF on shaded area = [LB-(d+d) (b+d)] Pucal.]

SF resisted by concrete Vu =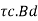

SF resisted by area = SF resisted by concrete

Find depth d

3.     d= maximum of the two calculated as above

4.     Depth required for bending moment

The bending moment is calculated at the face of the column as shown in fig.

Find the bending moment per meter width find the depth required for bending moment and check the depth provided for shear

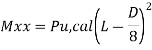
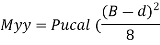
Md = maximum moment of the two calculated as follow

To find depth of footing equates Md to Mur

Mur = 0.149 fckbd^2

Mur =0.138 fck bd^2    fe 415

5.     Determine steel

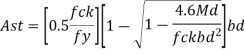
Provide this steel along each side

6.     Check for development length

Ld = 0.87 fy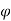/4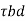

Check this length is available from the face of column in both directions.

7.     Summary and reinforcement details

The minimum depth a t the end of slope footing should not be less than 150mm

Examples 1 

Design an axially loaded short column at c 10 as shown in fig in ground floor and below plinth along the with isolated footing for G+2 building with following details:

1. Floor to floor height= 2.88 m
2. Depth of foundation below GL= 1.5 m
3. Height of plinth = 0.6 m
4. Live load on all slabs = 3 kN/m^2
5. Floor finish load = 1 KN/m^2
6. Water proofing loads on roof slab = 1.5 kN/m^2
7. Wall thickness = 230 mm
8. Slab thickness = 150 mm
9. Height pf parapet wall = 1 m
10. Size of beams = 230 x 450 mm
11. Safe bearing capacity of soil = 200 kN/m^2

Materials M25 and Fe415 used. Show detailed load design calculation and reinforcement details in plan and sectional elevation.

Solution:

Given:

Floor to floor ht. = 3.6 m

Ht. Of col below plinth= 2.5 m

L-L on all slabs = 4 KN/m^2

FF load = 1.5 KN/m^2

Water proofing load on root slab = 1.5 KN/m^2

Wall thickness = 150 mm

Slab thickness = 130 mm

Size of beams = 230 x 450 mm

Safe being capacity of soli = 220 KN/m^2

M25 and Fe 415

Step 1 Load on slab

1. Roof slab: dead load of soil = 25 D= 25x0.13 = 3.25 KN/m^2
2. Floor finish = 1.5 KN/m^2
3. Water proofing load = 1.5 kN/m^2
4. Line load on slab = 1.5 kN/m^2
5. Total load on roof slab = 7.75 KN/m^2

First and second floor slab:

Water proof is not required on first and second floor

Dead load on slab= 3.25 KN/m^2

Floor finish load = 1.5 KN/m^2

Live load = 4.0 KN/m^2

Total load on roof slab = 8.75 kN/m^2

Step 2 Load on slab to column

1. Load on column from roof slab

P = intensity of load x shaded area of floor

= 7.75 [ 3.805 x 3.16] = 93.18 kN

2.     Load on column from second floor slab

P= 8.75 (3.805 x 3.16) = 105. 208 kN

3.     Load on column from first floor slab

P= 8.75 (3.805 x 3.16) = 105.208 kN

Total load from slab to column = 93.18 +105.208 +105.208 = 303.60 kn

Step 3 beam load from floor to column

Self wt of beam = 25 bD = 25 x 0.23x 0.45= 2.5875 KN

W1 = 2.5875 KN

Wall load = density of masonary x twxH

W2 = 10.80 KN/m

1. Roof beam load to column = w1x length of beam of shaded portion

= 2.5875x(2.14+1.665+1.455+1.705) = 18.02 KN

2.     Second floor beam load to column

(w1+w2) length of beam shaded portion

= 93.24 KN

3.     First floor beam load to column= 93.24 KN

4.     Around the floor beam load to column = 93.24 KN

5.     Plinth beam load to column = 2.587 x 6.965 = 18.02KN/m

Total load inclusive self wt of beams

18.02 +(3x93.24) +18.02= 315.76 KN

Step 4 weight of column

Assume column size of beam = 230 mm x 500 mm

Self wt of column at floor level =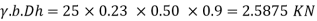

Self wt of column at second floor

Self wt of column at first floor = 2.875 x 3.6 = 10.35 kN

Self wt of column at ground floor = 10.35

Self wt of column from ground to plinth= 7.187 kN

Total load on column= 40.82 KN

Step 5 Total load on ground floor column

P= Slab load +beam load including wall load+ column load

P= 303.60+315.76+40.82 = 660 .18 kN

Step 6 Design load on column

= P+10% P for accidental increase in load

= 1.1 x660.18 = 726.20 kN

Step 7 Design of ground floor column

Factored design load Pu = 1.5 x 726.20 = 1089.29 KN

Assume area of steel 1% of gross area

Area of steel Asc= 3% Ag = 0.03Ag

Area of concrete Ac= Ag-Asc= 0.97Ag

Pu= 0.4 Fck Ac+0.67 fy Asc

Ag= 60382.35 m^2

Check for depth b= 230 mm

BD= 60382.35

D= 60382.35/230 = 262.53 mm<500 mm    ok

Provide size of column = 230 mm x500 mm

Area of steel Asc= 0.03 Ag= 0.03x230x500 = 3450 mm^2

Numbers of bars 22 mm

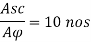
Provide 10 bars of 22 mm

Step 8 Check for minimum eccentricity

e min = left/500 +D/30 = 23. 86 mm

23.86 mm < 25 mm

Step 9 Design of lateral ties

Assume diameter of lateral ties is 8 mm

Pitch of lateral ties

1. Least lateral dimension=230 mm
2. 16 x diameter of longitudinal steel = 16x22 = 352 mm
3. 300 mm

Provide pitch = 230 mm

Summary

Column size = 230mm x 500 mm

Longitudinal steel = 10 bars of 22 mm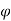

Lateral ties 8 mm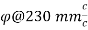

Design of column footing

Step 1 load on column = 1089.29 kN

Assume self wt of footing = 10x load on column

Total load on footing = 1.1 x 1089.29 = 1198.21 kN

Factored load on footing = 1.5 x 1198.21= 1797.33 kN

Step 2

Area of footing = factored load/ (ultimate safe bearing capacity of soil)

1797.32/220x2= 4.08 m^2

Step 3 Size of footing

b/D = B/L

B= b/D L

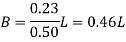
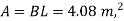
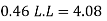
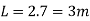
Provide size of rectangular footing 1.5 m x 3.0 m

Area provide Ap = 1.5 x 3.0 = 4.5 m^2

Step 4 Upward soil pressure

Upward soil pressure = Factored load on column/size of footing provided

Factored load on footing = load without self wt of footing

Step 5 Depth of footing

Depth of footing for BM criteria is consider on the face of column

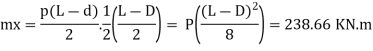
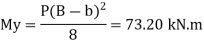
Maximum BM = 283.66 KN.m

Limiting moment of resistance Mu lim= 0.138 fck bd^2

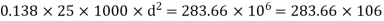
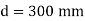
Overall depth D= d+c+= 300+40+25/2 = 400 mm provides

Design steps

Step 1: Transfer of axial force at the base of column

It is essential that the total factored load must be transferred at the base of columns without any reinforcement. For that the bearing resistance should be greater than the total factored load up

Pu = 1.5 × P

The bearing stress as per cl 34.4 of IS 456

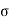b r = 0.45 f ck (A1/A2)1/2

With a condition that

(A1/A2)1/2 <= 2.0

Step 2: Size of the footing

Base area = P × 1.15 / 300

Provide B× D mm  .........assume A/2

Step 3: Thickness of footing

Tan 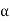<= 0.9 {(100 QA/f c k)+1}1/2

Therefore h = {(D - P)/2} (tan)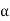

Provide B×D×h mm

Step 4: Minimum reinforcement

The plain concrete block B×D×h shall be provided with the minimum reinforcement 0.12 per cent for temperature, shrinkage and tie action

Minimum A s t = 0.0012 Bh

Step 5: Check for the gross base pressure

Assuming unit weight of concrete and soil as 24 KN/m3 and 20 kN/me

Service Load = P kn

Weight of footing = (0.67) (1.25) (1.25) (24)

Weight of soil = (0.33) (1.25) (1.25) (20)

Total = weight of footing + weight of soil + service load

Q a = total / (1.25) (1.25)

Step 6: Bending moment

Step 7: Development length of 12 mm diameter bars

Step 8: Providing slope in the footing slabs

Numerical

Problem 1

Design a plain concrete footing for a column of 400 mm x 400 mm carrying an axial load of 400 kN under service loads. Assume safe bearing capacity of soil as 300 kN/m at a depth of 1 m below the ground level. Use M 20 and Fe 415 for the design.

Solution 1:

Plain concrete footing is given in section .11.28.2(A)1 and 11.28.5(b).

Step 1: Transfer of axial force at the base of column

It is essential that the total factored loads must be transferred at the base of column without any reinforcement. For that the bearing resistance should be greater than the total factored load P

Here, the factored load P. = 400(1.5) = 600 kN.

The bearing stress, as per cl.34.4 of IS 456

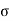= 0.45 f c k (A1/A2)1/2

With a condition that

(A1/A2)1/2 < 2.0

Since the bearing stress at the column-footing interface will be governed by the column face, we have A1 = A2 = 400(400) = 160000 mm2 Using A1 = A2 in Eq.

P b r = Bearing force = 0.45 f c k A1 = 0.45(20) (160000) (10^-3) = 1440 k N > P u (= 600 kN).

Thus, the full transfer of load P is possible without any reinforcement.

Step 2: Size of the footing

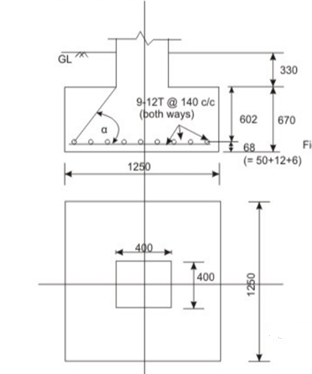
Fig no 1 Detailing

Let us assume the weight of footing and back fill soil as 15 per cent of P Then, the base area required = 400(1.15)/300 = 1.533 m2. Provide 1250 x 1250 mm (= 1.5625 m2) as shown in Fig. The bearing pressure q a = 400(1.15) / (1.25) (1.25) = 294.4 k N/m2.

Step 3: Thickness of footing

The thickness of the footing h is governed by Lesson 28. From below given by

Tan 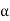<= 0.9 {(100 q a / f c k) + 1}1/2

Tan 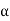<= 0.9 [{100(0.2944)/20} + 1]1/2

Tan 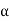<= 1.415

We have

h = ((1250 - 400)/2) (tan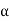) = 601.375 mm

Provide 1250 x 1250 x 670 mm block of plain concrete.

Step 4: Minimum reinforcement

The plain concrete block 1250 x 1250 x 670 shall be provided with the minimum reinforcement 0.12 percent for temperature, shrinkage and tie action.

Minimum A = 0.0012(1250) (670) = 1005.0 mm2

Provide 9 bars of 12 mm diameter (= 1018 mm2) both. The spacing of bars = (1250 - 50 - 12)/8 = 148.5 mm c/c. Provide the bars @ 140 mm c/c.

Step 5: Check for the gross base pressure

Assuming unit weights of concrete and soil as 24 kN/m and 20 kN/m

Service load = 400.00 kN

Weight of footing = (0.67) (1.25) (1.25) (24) = 25.125 KN

Weight of soil = (0.33) (1.25) (1.25) (20) = 10.3125 kN

Total = 435.4375 kN

Q a = 435.4375/ (1.25) (1.25) = 278.68 kN/m² < 300 kN/m2

Problem 2:

Design an isolated footing for a square column, 400 mm x 400 mm with 12-20 mm diameter longitudinal bars carrying service loads of 1500 kN with M 20 and Fe 415. The safe bearing capacity of soil is 250 kN/m² at a depth of 1 m below the ground level. Use M 20 and Fe 415.

Solution 2

Step 1: size of the footing

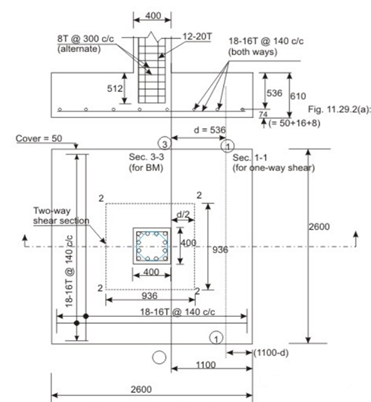
Fig no 2 Detailing

Given P = 1500 kN, g = 250 kN/m at a depth of 1 m below the ground level. Assuming the weight of the footing and backfill as 10 per cent of the load, the base area required = 1500(1.1)/250 = 6.6 m. Provide 2.6 m x 2.6 m, area = 6.76 m

Step 2: Thickness of footing slab based on one-way shear

Factored sol pressure = 1500(1.5)/ (2.6)2.6) = 0.3328 N/mm, say, 0.333 N/mm2

Assuming p= 0.25% in the footing slab, tor M 20 concrete, Tc= 0.36 N/mm (Table 19 of IS 456). Vu - 0.36(2600) d and V u(actual) = 0.333(2600) (1100-d). From the condition that should be more than or equal to the actual V we have

0.36(2600) d >= 0.333(2600) (1100-d)

So, d >= 528.57 mm.

Provide d = 536 mm. The total depth becomes 536 + 50 + 16 + 8 (with 50 mm cover and diameter of reinforcing bars = 16 mm) = 610 mm.

Step 3: Checking for two-way shear

The critical section is at a distance of d/2 from the periphery of the column The factored shear force (Fig. 11.29.2b, sec. 2222) = 0.333{(2600)2 - (400 + d)2} (10^-3) = 1959.34 kN. Shear resistance is calculated with the shear strength = ks Tc = ks (0.25) (f c k)^1/2 where k s = 0.5 + B c (cl. 31.6.3 of IS 456). Here B c= 1.0, ks = 1.5 > 1; so ks = 1.0. This gives shear strength of concrete = 0.25 (f c k)^1/2 = 1.118 N/mm2. So, the shear resistance (1.118) 4 (936) (536) = 2243.58 kN > 1959.34 kN. Hence, ok.

Thus, the depth of the footing is governed by one-way shear.

Step 4: Gross bearing capacity

Assuming unit weights of concrete and soil as 24 kN/m and 20 k N/mm respectively:

Given the service load = 1500 kN

Weight of the footing = 2.6(2.6) (0.61) (24) = 98.967 N

Weight of soil = 2.6(2.6) (1.0-0.61) (20) = 52.728 kN (Assuming depth of the footing as 1.0 m)

Total = 1635.2 KN

Gross bearing pressure = 1635.2/ (2.6) (2.6) = 241.893 k N/m2 < 250 k N/m2. Hence, ok.

Step 5: Bending moment

The critical section (Fig.11.29.2b, sec.3.3), is at the face of the column.

Mu = 0.333(2600) (1100) (550) Nmm = 523 809 kNm

Moment of resistance of the footing = Rbd2 where R= 2.76

Moment of resistance = 2.76(2600) (536) (536) = 2061.636 kNm > 523.809 kNm.

Area of steel shall be determined which is

Mu = 0.87 ft A s t d {1 - (A s t ft /f c k BD)}

Substituting Mu = 523.809 k Nm, f y = 415 N/mm2, f c k = 20 N/mm2, d= 536 mm, b = 2600 mm, we have:

Solving, we get Au = 2825.5805 mm2

Alternatively, we can use Table 2 of SP-16 to get the Au as explained below:

Mu/bd2 = 523.809(10^6)/ (2600) (536) (536) = 0.7013 N/mm2. Table 2 of SP-16 gives p = 0.2034.

A s t = 0.2034(2600) (536)/100 = 2834.58 mm2

This area is close to the other value = 2825.5805 mm2

However, one-way shear has been checked assuming p= 0.25%. So, use p= 0.2. A s t =0.0025(2600) (536) = 3484 mm2.

Provide 18 bars of 16 mm diameter (= 3619 mm2) both ways. The spacing of bars = {2600 - 2(50) - 16}/17 = 146.117 mm. The spacing is 140 mm c/c

The bending moment in the other direction is also the same as it is a square footing. The effective depth, however, is 16 mm more than 536 mm. But, the area of steel is not needed to be determined with d = 552 mm as we are providing 0.25 per cent reinforcement based on one-way shear checking

Step 6: Development length

Ld = f s /4 () = 0.87(415) (16)/4(1.6) (1.2) = 47(16) = 752 mm (cl.26.2.1 of IS 456)

Length available = 1100 - 50 = 1050 mm > 752 mm.

Step 7: Transfer of force at the base of the column

P = 1500(1.5) = 2250 kN

Compressive bearing resistance = 0.45 f c k (A1/A2)1/2. For the column face A1/A2 = 1 and for the other face A1/A2 > 2 but should be taken as 2. In any case, the column face governs

Force transferred to the base through column at the interface = 0.45(20) (400) (400) = 1440 kN < 2250 kN. The balance force 2250 - 1440 = 810 kN has to be transferred by the longitudinal reinforcements, dowels or mechanical connectors. As it is convenient, we propose to continue the longitudinal bars (12-20 mm diameter) into the footing.

The required development length of 12-20 mm diameter bars, assuming a stress level of 0.871 fy (810/2250) = 129.978 N/mm2, is 129.978(20)/4(1.6) (1.2) (1.25) = 270.8 mm. Here b d for M 20 = 1.2 N/mm2, increased factor of 1.6 is due to deformed bars and increased factor of 1.25 is for the compression

Length available = 610 - 50 - 16 - 16 - 16 = 512 mm > 270.8 mm. Hence, ok. The arrangement is shown in below fig

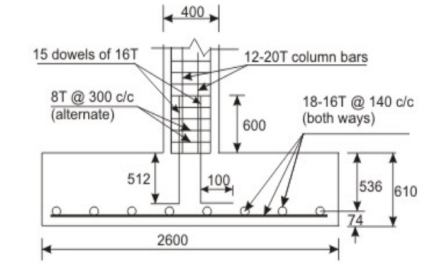
Fig no 3 Detailing

For the balance force 810 kN, the area of dowels = 810000/0.67(415) = 2913.15 mm2. Minimum area=0.5(400) (400)/100 = 800 mm2 < 2913.15 mm2 (cl.34.4.3 of IS 456). Therefore, number of 16 mm dowels = 2913. 15/201 = 15. The development length of 16 mm dowels in compression = 0.87(415) (16)/4(1.6) (1.2) (1.25) = 601.76 mm. Available vertical embedment length = 610 - 50 - 16 - 16 - 16 = 512 mm. So, the dowels will be extended by another 100 mm horizontally, as shown in fig

Problem 3:

Design a sloped footing for a square column of 400 mm x 400 mm with 16 longitudinal bars of 16 mm diameter carrying a service load of 1400 KN. Use M 20 and Fe 415 both for column and footing slab. The safe bearing capacity of soil is 150 kN/m,

Solution 3

Step 1: Size of footing

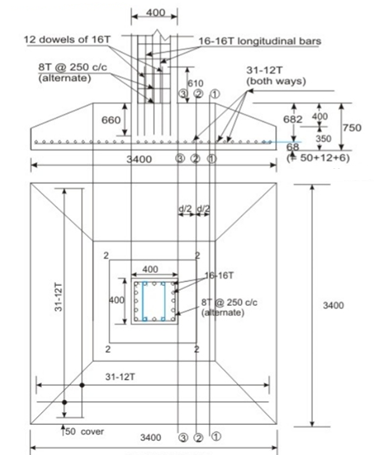
Fig no 4 Detailing

Given P = 1400 KN and q c = 150 KN/m2. Assuming the weight of the footing and the back file as 10 per cent of the load the required base area is: 1400(1.1)/150 = 10.27 m2. Provide 3400 x 3400 mm giving 11.56 m2

Step 2: Thickness of footing slab based on one-way shear

Factored bearing pressure = 1400(1.5)/ (3.4) (3.4) = 181.66 k N/m2 = 0.18166 N/mm2. Assuming 0.15 per cent reinforcement in the footing slab Table 19 of IS 456 gives for M 20 = 0.28 N/mm2.  From the condition that the one-way shear resistance >= one-way shear force, we have at a distance from the face of the column

0.28(3400) d >= 0.18166(1500 - d) (3400)

Or d >= 590.24 mm.

Provide total depth of footing as 670 mm, so that the effective depth = 670 - 50 -16 - 8 = 596 mm. (The total depth is, however, increased to 750 mm in Step 7)

Step 3: Checking for two-way shear

At the critical section 2222 the shear resistance = 4(400 + 596) (596) (0.25) (f c k) ^1/2 = 2654.73 KN.

The Shear force {(3.4) (3.4) - (0.996) (0.996))0.18166 = 1919.78 KN < 2654.73 k N. Hence

Step 4: Gross bearing capacity

Assuming unit weights of concrete and soil as 25 kN/m3 and 18 k N/m3respectively, we have:

Load on footing = 1400.00 kN

Weight of footing = (3.4) (3.4) (0.67) (25) = 193.63 kN

Weight of soil = (3.4) (3.4) (1.25 - 0.67) (18) = 120.69 KN (Assuming the depth of the footing as 1.25 m).

Total = 1714.32 KN

Gross bearing capacity = 1714.32 / (3.4) (3.4) = 148.30 k N/m < 150 k N/m2. Hence ok

Step 5: Bending moment

We have to determine the area of steel in one direction as it is a square footing. So, we consider the lower effective depth which is 596 mm. The critical section is sec.33 where we have

Mu = 3400(1500) (0.18166) (1500)/2 = 694.8495 kNm

Mu /bd2 = 694.8495(10^6)/ (3400) (596) (596) = 0.575 N/mm2

Table 2 of SP-16 gives, p = 0.165%. Accordingly, area of steel = 0.165(3400) (596)/100 = 3343.56 mm2. Provide 30 bars of 12 mm diameter (= 3393 mm2), both ways.

Step 6: Development length

Development length of 12 mm diameter bars - 0.87(415) (12)/4(1.6) (1.2) = 564.14 mm, Hence, ok

Step 7: Providing slope in the footing slab

Since the three critical sections (I e, of bending moment, two-way shear and one-way shear) are within a distance of 596 mm from the face of the column the full depth of the footing slab is provided up to a distance of 700 mm from the face of the column. However, by providing slope the available section now is a truncated rectangle giving some less area for the one-way shear.

Accordingly, the depth of the footing is increased from 670 mm to 750 mm. With a cover of 50 mm and bar diameter of 12 mm in both directions, the revised effective depth = 750 - 50 - 12 - 6 = 682 mm. Providing the minimum depth of 350 mm at the edge, as shown in Figs. 11.29.3a and b, we check the one-way shear again taking into account of the truncated rectangular cross-section at a distance of 682 mm from the face of the column.

One-way shear force = 0.18166(1500 - 682) (3400) = 505232.792 N

Area of truncated rectangle = 1800(682) + 1600(282) + 1600(682-282)/2

=1998800 mm

The shear stress = 505232.792/1998800 = 0.2527 N/mm2 < 0.28 N/mm2.

Hence ok.

Step 8: Revised area of steel

The bending moment in step 5 is 694 8495 kNm at the face of the column. With d= 682 mm now, we have

Mu/bd2 = 694.8495(10^6)/ (3400) (682) (682) = 0.4394 N/mm2

Table 2 of SP-16 gives p is less than 0.15 percent. Provide p=0.15 percent due to the one-way shear. So, A s t= 0.15(3400) (682)100 = 3478.2 mm2. Provide 31 bars of 12 mm (A s t = 3506 mm2), both ways. Effectively, the number bars have increased from 30 to 31 now

Step 9: Transfer of force at the base of the column

P u = 1400(1.5) = 2100 kN. Compressive bearing resistance = 0.45

F c k (A1/A2)1/2 = 0.45(20)(1) = 9 N/mm2.

Force transferred at the base through the column = 9(400) (400) (10^-3) = 1440 kN < 2100 kN.

Provide dowels for the excess (2100 - 1440) - 660 KN. The area of dowels = 660(10^3)/ (0.67) (415) = 2373.67 mm2. Minimum area of dowels = 0.5(400) (400) /100 = 800 mm2. Provide 12 dowels of 16 mm diameter (area 2412 =mm2)

The development length of 16 mm dowels = 0.87(415) (16) /4(1.6) (1.2) (1.25) = 601.76 mm.

The vertical length available 750 - 50 - 12 - 12 - 16 = 660 mm > 601.76 mm. Hence, ok.

Whenever two or more columns in a straight line are carried with one foot spread, it is called a composite foot. The separated feet of each column are usually economical.

Combined feet are provided only when they are most needed, as

1. When two columns are close together, they form a series of adjacent layers

2. When the carrying capacity of the soil is low which causes the formation of adjacent independent feet.

3. Proximity to the building line or existing building or sewage, adjacent to the building column.

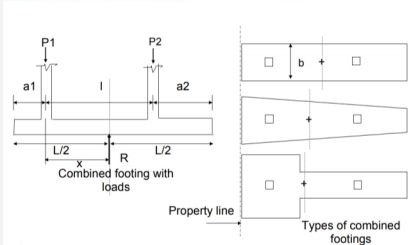
Fig no 5 Combined footing

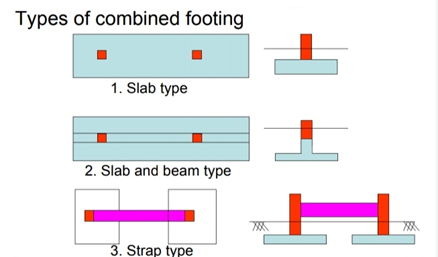
Fig no 6 Types of footing

The jointed foot can be rectangular, trapezoidal or shaped like a Tee in order.

The geometric size and configuration are set in such a way that of the foot area corresponds to the effect of the column loads. This leads to the same pressure under the entire foot area.

Trapezoidal foot is provided when one column load is significantly higher than the other. As a result, both movement rates over the surface of the columns will be limited.

A rectangular foot is provided where any treadmill is restricted or the width of the foot is restricted.

Rectangular combined footing

Over time, the foot acts as a loaded beam that falls between the columns and the upper cantilevering. Statistics, shaving power and temporary bending curves are used in the long-distance direction. The time is checked on the face of the column. Shear strength is most important in the d range in the surface of the columns or where the resistance is reversed. Two-shear shear is tested under a heavy column.

The foot also has a flexible curve and this bend spreads over a short clip near the foot

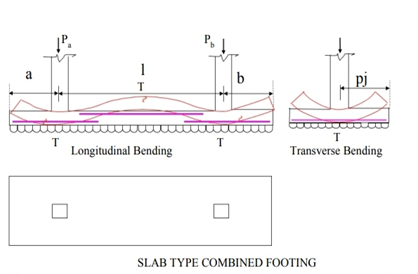
Fig no 7 Slab type combined footing

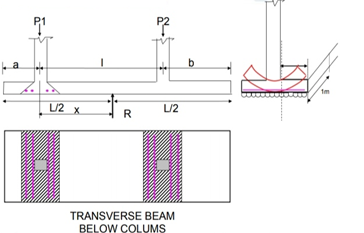
Fig no 8 Transverse beam

Design Steps

Find the point of use of column loads on foot.

Align the foot so that the effect of the load passes through the center of the foot,

Calculate the area of ​​the foot so that the soil is allowed the pressure does not exceed

Calculate shear strength and bending times in important points therefore draw SFD and BMD.

Adjust the depth of the feet from the upper bend a moment.

Calculate the passing moment of the pass and arrange the shortcut section in depth and reinforcement. See anchorage and shear.

Design Steps

Look at the base of the longitudinal shear so form a longitudinal shear

Create minute-length reinforcement and place them in the right places.

Check the length of the development of the long metal

Reduce long-term economic barriers • Draw and provide reinforcement information

Adjust the bar bending system

Detailing

The metal details (both length and length) on the jointed feet are similar to those of the standard SP-34 beam

The required details of the beams and slabs should be followed as appropriate-SP-34

NUMERICAL

Design of combined footing - Slab and Beam type

1. Two interior columns A and B carry 700 kN and 1000 kN loads respectively. Column A is 350 mm x 350 mm and column B is 400 mm X 400 mm in section. The centre to centre spacing between columns is 4.6 m. The soil on which the footing rests is capable of providing resistance of 130 kN/m2. Design a combined footing by providing a central beam joining the two columns. Use concrete grade M25 and mild steel reinforcement.

Draw to a suitable scale the following

1. The longitudinal sectional elevation

2. Transverse section at the left face of the heavier column

3. Plan of the footing

Solution:

Data

F c k = 25 N/mm2

F y = 250 N/mm2

F b = 130 kN/m2 (SBC),

Column A = 350 mm x 350 mm,

Column B = 400 mm x 400 mm,

C /c spacing of columns = 4.6 m,

PA = 700 kN and PB = 1000 kN

Required: To design combined footing with central beam joining the two columns.

Ultimate loads

P A= 1.5 x 700 = 1050 k N, P B = 1.5 x 1000 = 1500 kN

Proportioning of base size

Working load carried by column A = PA = 700 kN

Working load carried by column B = PB = 1000 kN

Self-weight of footing 10 % x (PA + PB) = 170 kN

Total working load = 1870 kN

Required area of footing = Af = total load/SBC

=1870/130 = 14.38 m2

Let the width of the footing = Bf = 2m

For uniform pressure distribution the C.G. Of the footing should coincide with the C.G. Of column loads. Let x be the distance of C.G. From the centre line of column A

Then x = (PB x 4.6)/ (PA + PB) = (1000 x 4.6)/ (1000 +700) = 2.7 m from column A.

If the cantilever projection of footing beyond column A is 'a' then, a + 2.7 = Lf /2 = 7.2/2, Therefore a = 0.9 m

Similarly, if the cantilever projection of footing beyond B is 'b' then, b + (4.6-2.7) = Lf /2= 3.6 m,

Therefore b = 3.6 - 1.9 = 1.7 m

The details are shown in Figure

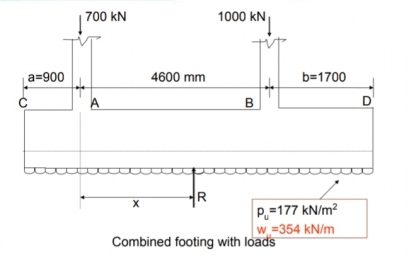
Fig no 9 Combined footing with loads

Rectangular Footing with Central Beam:

Design of Bottom slab

Total ultimate load from columns = Pu = 1.5(700 + 1000) = 2550 kN.

Upward intensity of soil pressure Wu = P/A f= 2550/14.4 =177 kN/m2

Design of slab

Intensity of Upward pressure = wu =177 kN/m2

Consider one meter width of the slab (b=1m)

Load per m run of slab at ultimate = 177 x 1 = 177 kN/m

Cantilever projection of the slab (For smaller column)

=1000 - 350/2 = 825 mm

Maximum ultimate moment = 177 x 0.8252/2 = 60.2 kN-m.

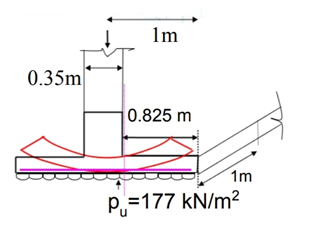
Fig no 10

For M25 and Fe 250, Q u max = 3.71 N/mm2

Required effective depth = √ (60.2 x 10^6 / (3.71 x 1000)) = 128 mm

Since the slab is in contact with the soil clear cover of 50 mm is assumed.

Using 20 mm diameter bars

Required total depth = 128 + 20/2 + 50 =188 mm say 200 mm Provided effective depth = d =200-50-20/2 = 140 mm

To find steel

Mu/bd2 =3.07<3.73, URS

Mu =0.87 f y A s t [d-f y A s t / (f c k b)]

Pt =1.7%

A s t = 2380 mm2

Use 20 mm diameter bar at spacing = 1000 x 314 / 2380 = 131.93 say 130 mm c/c

Area provided = 1000 x 314 / 130 = 2415 mm2

Check the depth for one-way shear considerations- At d from face

Design shear force= Vu =177x (0.825-0.140) = 121KN

Nominal shear stress= =Vu /bd=121000/(1000x140) =0.866MPa

Permissible shear stress

Pt = 100 x 2415 / (1000 x 140) = 1.7 %,

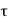u c= 0.772 N/mm2

Value of k for 200 mm thick slab = 1.2

Permissible shear stress = 1.2 x 0.772 = 0.926 N/mm2 > and hence safe

The depth may be reduced uniformly to 150 mm at the

Check for development length

L d t = [0.87 x 250 / (4 x 1.4)] =39

= 39 x 20 = 780 mm

Available length of bar=825 - 25 =800mm > 780 mm and hence safe.

Transverse reinforcement

Required A s t =0.15bD/100

=0.15x1000 x 200/100 = 300mm2

Using 8 mm bars, Spacing=1000x50/300 = 160 mm

Provide distribution steel of 8 mm at 160 mm c/c. <300, <5d

Design of Longitudinal Beam

Load from the slab will be transferred to the beam. As the width of the footing is 2 m, the net upward soil pressure per meter length of the beam = Wu = 177 x 2 = 354 kN/m

Shear Force and Bending Moment

V a c= 354 x 0.9 =318.6 kN, VAB = 1050-318.6 =731.4 kN

V B d = 354 x 1.7 = 601.8kN, VBA = 1500-601.8 = 898.2 kN

Point of zero shears from left end C

X1 = 1050/354 = 2.97m from C or

X2 = 7.2-2.97 = 4.23 m from D

Maximum B.M. Occurs at a distance of 4.23 m from D, MuE = 354 x 4.23^2/2 - 1500 (4.23 - 1.7) = -628 kN.m

Bending moment under column A= M u A =354x0.9^2 /2 = 143.37 kN.m

Bending moment under column B = MuB = 354 x 1.7^2 = 511.5 kN-m

Let the point of contra flexure be at a distance x from the centre of column A

Then, Mx = 1050x - 354 (x + 0.9)^2/2 = 0

Therefore x = 0.206 m and 3.92 m from column A i.e., 0.68 m from B.

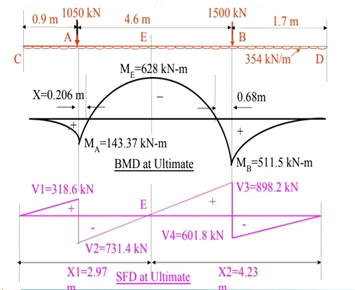
Fig no 11 SFD and BMD

Depth of beam from B.M.

The width of beam is kept equal to the maximum width of the column i.e., 400 mm. Determine the depth of the beam where T- beam action is not available. The beam acts as a rectangular section in the cantilever portion, where the maximum positive moment = 511.5 kN/m.

d =√ (511.5 x 10^6 / (3.73 x 400)) = 586 mm

Provide total depth of 750 mm. Assuming two rows of bars with effective cover of 70 mm.

Effective depth provided = d= 750-70 = 680 mm (Less than 750mm and hence no side face steel is needed.

Check the depth for Two-way Shear

The heaver column B can punch through the footing only if it shears against the depth of the beam along its two opposite edges, and along the depth of the slab on the remaining two edges. The critical section for two-way shear is taken at distance d/2 (i.e., 680/2 mm) from the face of the column. Therefore, the critical section will be taken at a distance half the effective depth of the slab (ds/2) on the other side as shown in Fig.

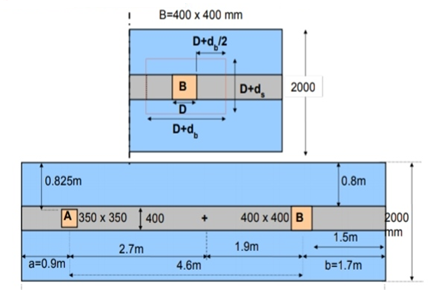
Fig no 12 Detailing

In this case b=D=400 mm, db =680 mm, ds = 140 mm

Area resisting two - way shear = 2(b x db + ds x d s) +2 (D + d b) ds

= 2 (400 x 680+ 140 x 140) + 2(400+680) 140= 885600 mm2

Design shear =Pu d = column load - Wu x area at critical section

= 1500 - 177 x (b + d s) x (D + db)

= 1500-177 x (0.400+0.140) x (0.400+ 0.680) =1377.65KN

T v =P is/ bo d= 1377.65x1000/885600= 1.56 MPa

Shear stress resisted by concrete = T ­u c = T u c × Ks

Where, u c= 0.25 √fck = 0.25 √25 = 1.25 N/mm²

Ks = 0.5 + d/D = 0.5 + 400/400 = 1.5 <1 Hence K s= 1

u c= 1 x 1.25 = 1.25 N/mm2 Therefore Unsafe

Area of Steel: Cantilever portion BD

Length of cantilever from the face of column

=1.7- 0.4/2 = 1.5 m.

Ultimate moment at the face of column =354x1.5^2/2 =398.25 kN-m

Mu max = 3.71 x 400 x 680^2 x 10^ -6 = 686 kN-m > 398.25 kN-m

Therefore, Section is singly reinforced.

Mu/bd^2 =398.25x10^6 /(400x680^2) = 2.15<3.73, URS

Pt =1.114%

A s ­t =3030 mm2, Provide 3- 32 mm + 4- 16 mm at bottom face,

Area provided = 3217 mm2

L d t = 39 x 32 = 1248 mm

Curtailment

All bottom bars will be continued up to the end of cantilever. The bottom bars of 3- 32 will be curtailed at a distance d (= 680 mm) from the point of contra flexure (a = 680 mm) in the portion BE with its distance from the centre of support equal to 1360 mm from B.

Cantilever portion AC

Length of cantilever from the face of column =900-350/2 = 725 mm

Ultimate moment 354 x 0.7252 /2 = 93 kN-m

Mu /bd2 =93x10^6/(400x6802) =0.52 <3.73, URS

Pt =0.245% (Greater than minimum steel)

A s t =660 mm2

Provide 4 - 16 mm at bottom face, Area provided 804 mm2 Continue all 4 bars of 16 mm diameter throughout at bottom.

Region AB between points of contra flexures

The beam acts as an isolated T-beam.

b = [Lo/ (Lo/b +4)] + b w where,

Lo = 4.6 - 0.206 - 0.68 = 3.714 m = 3714 mm

b= actual width of flange = 2000 mm, bw = 400 mm

Bf = [3714/ (3714/2000+4) + 400] =1034mm < 2000mm

Df =200 mm, Mu = 628 kN-m

Moment of resistance M u f of a beam for xu = D f is:

Muf = [0.36 x 25 x1034 x 200(680 - 0.42x200)]x10^-6 = 1109 kN.m > Mu (= 628 kN-m)

Therefore Xu <Df

Mu =0.87 f y A s t (d-f y A s t /f c k bf)

A s t = 4542 mm2

Provide 5 bars of 32 mm and 3 bars of 16 mm,

Area provided = 4021 + 603 = 4624 mm2 >4542 mm2

P t = 100 x 4624/(400x680) = 1.7%

Curtailment:

Consider that 2- 32 mm are to be curtailed

No. Of bars to be continued = 3 - 16 + 3 - 32

Given area = A s t =3016 mm2

Moment of resistance of continuing bars

Mur = (0.87 x 250 x 3016 (680 - ((250 x 3016) / (25 x 400) x 10-6 = 396.6 kN-m

Let the theoretical point of curtailment be at a distance x from the free end C,

Then, M u c = Mur Therefore -354 x²/2 + 1050 (X-0.9) = 396.6 x^2- 5.93x + 7.58 =0,

Therefore x = 4.06m or 1.86m from C

Actual point of curtailment = 4.06 + 0.68 = 4.74 m from C or 1.86 - 0.68 = 1.18 m from C

Terminate 2-phy 32 mm bars at a distance of 280 mm (= 1180 - 900) from the column A and 760mm (= 5500 - 4740) from column B. Remaining bars 3 - 32 shall be continued beyond the point of inflection for a distance of 680 mm i.e., 460 mm from column A and up to the outer face of column B. Remaining bars of 3 - 16 continued in the cantilever portion.

Design of shear reinforcement Portion column i.e., AB

In this case the crack due to diagonal tension will occur at the point of contra flexure because the distance of the point of contra flexure from the column is less than the effective depth d (= 680mm)

(i) Maximum shear force at B = V umax = 898.2 kN

Shear at the point of contra flexure = VuD - 898.2-354 x 0.68 = 657.48 kN

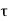v=657000/(400x680) =2.42 M Pa <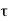c, max

Area of steel available 3 - 16 + 3 - 32

A s t = 3016 mm2

Pt = 100 x 3016 / (400 x 680) = 1.1%

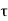c=0.664MPA

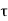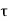v>c

Design shear reinforcement is required.

Using 12 mm diameter 4 - legged stirrups

Spacing= [0.87 x 250x(4x113)]/ (2.42-0.664) x400 =139 mm

Say 120 mm c/c

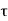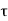Zone of shear reinforcements between v to  c

= m from support B towards A

(ii) Maximum shear force at A = Vu max = 731.4 kN.

Shear at the point contra flexure = V uD = 731.4 - 0.206 x 354 = 658.5 KN

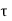v =658500/(400x680) =2.42MPa <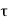c max

Area of steel available = 4624 mm2 pt = 100 x 4624 / (400 × 680) = 1.7 %

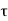u c= 0.772 N/mm2

Design shear reinforcement is required.

Using 12 mm diameter 4 - legged stirrups,

Spacing = 0.87 x 250 x (4 x 113)/ (2.42-0.774) x400 =149 mm say 140 mm c/c

Zone of shear reinforcement

From A to B for a distance as shown in figure

For the remaining central portion of 1.88 m provide minimum shear reinforcement using 12 mm diameter 2 - legged stirrups at

Spacing, s = 0.87 x 250 x (2 x 113/ (0.4 x 400) =307.2 mm, Say 300 mm c/c< 0.75d

Cantilever portion BD

V umax = 601.8kN,

V uD =601.8-354(0.400/2 + 0.680) = 290.28kN

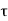v=290280 / (400x680) =1.067MPA <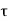c max

A at = 3217 mm² and pt = 100 x 3217/ (400 x 680) = 1.18%

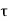c =0.683N/mm² (Table IS:456-2000)

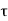v>cand v- c <0.4 Provide minimum steel.

Using 12 mm diameter 2- legged stirrups, 43-44/48 Spacing = 0.87 x 250 x (2 x 113)/ (0.4x400) = 307.2 mm say 300 mm c/c

Cantilever portion AC

Minimum shear reinforcement of 12 mm diameters 2 - legged stirrups at 300mm c/c will be sufficient in the cantilever portions of the beam as the shear is very less.

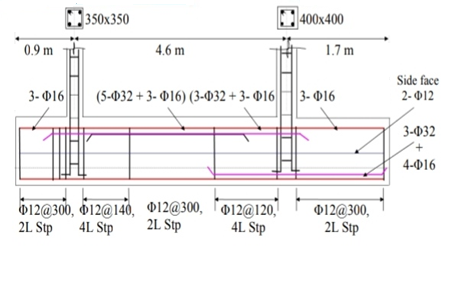
Fig no 13 Steel in footing

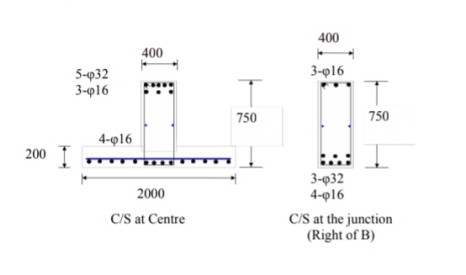
Fig no 14 Reinforcement

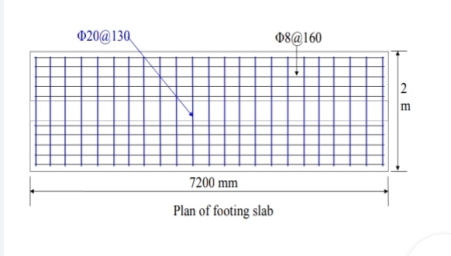
Fig no 15 Reinforcement detailing

Key takeaways:

Design steps for combined footing

1. Find the point of use of column loads on foot.
2. Align the foot so that the effect of the load passes through the center of the foot,
3. Calculate the area of ​​the foot so that the soil is allowed the pressure does not exceed
4. Calculate shear strength and bending times in important points therefore draw SFD and BMD.
5. Adjust the depth of the feet from the upper bend a moment.
6. Calculate the passing moment of the pass and arrange the shortcut section in depth and reinforcement. See anchorage and shear.

Design steps for isolated footing

1. Proportion of footing for column

2. Check for bending moment

3. Check for one-way shear

4. Check for two-way shear

5. Check for bearing stress

6. Check for development length

Case Study

1. Column

Axially Loaded Short Columns with Minimum Eccentricity Requirement

Assumptions (Clause 39.1 of IS456: 2000)

(1) The maximum compressive strain in concrete in axial compression is taken as 0.002

(2) Strain in concrete and steel are equal.

(3) The maximum compressive strain at the highly compression extreme fiber in concrete subjected to axial compression and bending and when there is no tension on the section shall be 0.0035 minus 0.75 times the strain at the least compressed extreme fiber.

(4) Stress in steel is governed by characteristic stress-strain curve of steel in compression. The stress-strain curve of steel in compression is the same as in tension.

(5) The column is short.

Equation for Short Axially Loaded Tied Columns (Clause39.3 of IS456: 2000)

According to Clause 39.3 of IS456 2000, when the eccentricity does not exceed 0.05 times the lateral dimension, the member may be designed by the following equation.

P u= 0.4fck Ac+0.67fy.Asc

Where Pu = factored axial load on the member,

Fck = characteristics compressive strength

Ac = area of concrete

Fy = Characteristics strength of the compression reinforcement

Asc = area of longitudinal reinforcement for column.

Equation of Short Axially Loaded

Columns with Helical Ties (Clause39.4 of IS 456: 2000)

The code further recommends that the ratio of volume of helical reinforcement to the volume of core shall not be less than 0.36 (A/A, -1) (fa/), in order to apply the additional strength factor of 1.05 (Clause 39.4.1). Accordingly, the governing equation of the spiral columns may be written as

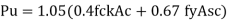
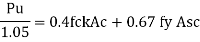
The pitch of helical reinforcement is determined using the following relation as per C1 39.4.1 of IS456 2000.

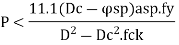
Where Dc = Diameter of concrete core,

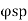= Diameter of spiral reinforcement,

Asp= Area of cross-section of spiral reinforcement,

P= Pitch of spiral reinforcement.

Note: The pitch and diameter of the spiral reinforcement should also satisfy Clause 26.5.3.2 of IS456: 2000.

Design Procedure for Axially Loaded Short Columns

Step 1: Find effective length.

Step 2: Find the minimum eccentricity and check the type of column.

Step 3: Find the area of steel

Use, Pu = 0.4fck Ac+0.67fy, Asc

Step 4: Design of lateral ties

The diameter of transverse reinforcement (lateral ties) is determined from Clause 26.5.3.2 C-2 of IS456 as not less than

(i)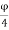 and

(ii) 6 mm.

The pitch of lateral ties, as per Clause26.5.3.2 C-1 of IS456, should be not more than the least of

(i) Sixteen times the smallest diameter of longitudinal reinforcement bar to be tied.

(ii) The least lateral dimension of the column.

(iii) 300 mm

Step 5: Draw the cross section.

B.    Footing

The following are the steps as how the footing design is being proceded-

1. Proportion of footing for column

2. Check for bending moment

3. Check for one-way shear

4. Check for two-way shear

5. Check for bearing stress

6. Check for development length

Isolated Column Footings

Used for single column. It may be square, circular or rectangular. The footing is of R.C.C with reinforcement at bottom. Column footing on piles should have a minimum thickness of 30 cm

Thickness of Footing Base Slab

The thickness of a footing base slab is generally based on considerations of shear and flexure, which are critical near the column location.

Generally, shear considerations predominate, and the thickness is based on shear criteria.

Except in the case of small footings, it is economical to vary the thickness from a minimum at the edge to a maximum near the face of the column, in keeping with the variations in bending moment and shear force. This may be achieved either by sloping the top face of the base slab or by providing a stepped footing.

In any case, the IS456 2000 Code (Clause 34.1.2) restricts the minimum thickness at the edge of the footing to 150 mm for footings in general (and to 300 mm in the case of pile caps). This is done to ensure that the footing has sufficient rigidity to provide the calculated bearing pressures.

A 'leveling course of lean concrete (about 100 mm thick) is usually provided below the footing base

Design Considerations

(a) Minimum nominal cover (Clause 26.4.2.2 of IS456)

The minimum nominal cover for the footings should be more than that of other structural elements of the superstructure as the footings are in direct contact with the soil

Clause 26.4.2.2 of IS 456 prescribes a minimum cover of 50 mm for footings

The actual cover may be even more depending on the presence of harmful chemicals or minerals, water table etc.

(b) Thickness at the edge of footings

(Clause 34.1.2 and 34.1.3 of IS 456)

The minimum thickness at the edge of reinforced and plain concrete footings shall be at least 150 mm for footings on soils and at least 300 mm above the top of piles for footings on piles, as per the stipulation in Clause 34.1.2 of 15456.

For plain concrete pedestals. The angle a (see Fig. 9.12.1) between the plane passing through the bottom edge of the pedestal and the corresponding junction edge of the column with pedestal and the horizontal plane shall be determined from the following expression. (Clause 34.1.3 of 15456)

Tan a ≤ 0.90((100q, /) +1)

Where,

Qa, calculated maximum bearing pressure at the base of pedestal in N/mm², and

Fck = characteristic strength of concrete at 28 days

(c) Bending moments (Clause 34.2 of IS 456)

The critical section of maximum bending moment for the purpose of designing an isolated concrete footing which supports a column, pedestal or wall shall be:

(1) At the face of the column, pedestal or wall for footing supporting a concrete column, pedestal or reinforced concrete wall, and

(ii) Halfway between the centre-line and the edge of the wall, for footing under masonry wall. This is stipulated in Clause 34.2.3.2 of 15456.

(d) Shear force (Clause 31.6 and 34.2.4 of IS456)

Footing slabs shall be checked in one-way or two-way shears depending on the nature of bending. If the slab bends primarily in one-way, the footing slab shall be checked in one-way vertical shear. On the other hand, when the bending is primarily two-way, the footing slab shall be checked in two-way shear or punching shear

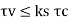
Where k, = 0.5 +Bc

Bc Short side of column /Long side of column

The respective critical sections and design shear strengths are given below

2.     One-way shear (Clause 34.2.4 of IS456)

One-way shear has to be checked across the full width of the base slab on a vertical section located from the face of the column, pedestal or wall at a distance equal to effective depth of the footing slab in case of footing slab on soil, and the design shear strength of concrete without shear reinforcement is given in Table 19 of Clause 40.2 of 1S456 or Table 6.6.1

Critical section for shear is assumed as a vertical section located from the face of column at a distance equal to

Where d = effective depth of footing

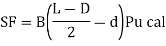
2 Two-way or punching shear (Clause31.6 and 34.2.4)

Two-way or punching shear shall be checked around the column on a perimeter half the effective depth of the footing slab away from the face of the column or pedestal. Normally, the thickness of the base slab is governed by shear. Hence, the necessary thickness of the slab has to be provided to avoid shear reinforcement.

S.F. On shaded area= [LB-(d+D) (b+d)] Pu, cal

References:

1. Design of Reinforced Concrete Structure by N. Subramanian, Oxford University Press

2. Limit State Design by A.K. Jain, Neemchand & Bros

3. Reinforced Concrete Design by S U Pillai & D. Menon, McGraw Hill

4. Design of concrete structures by J.N. Bandyopadhyay, PHI

5. Limit State Design of Reinforced Concrete -P.C Verghese