Unit - 1
Properties of concrete and reinforcing steel
Concrete is strong in compression but weak in tension.
Steel is reinforced suitable at the place where concrete is weak in tension. Such combination of steel and concrete is called as reinforced concrete.
Reinforced concrete is used to construct various structures
(1) Buildings
(2) Bridges
(3) Flyovers
(4) Water Tanks
(5) Retaining Walls
(6) Bunkers and silos
(7) Chimney
(8) Towers
(9) Concrete roads
1. Working Stress Method (W)
2 Ultimate Load Method (ULM)
3. Limit State Method (LSM)
Limitations of WSM methods over LSM
1. Since WSM based on elastic theory, the reserve strength materials beyond yield point are not taken into account.
2. In working stress method, serviceability criteria is not taken into consideration, moment of resistance for same cross section is more in LSM than WSM.
Advantages of Reinforced Concrete
Advantages of Reinforced concrete is as follows
1. Strength
2. Ductility
3. Durability
4. Mouldability
5. Permeability
6. Fire resistance
7. Economy
1. Strength
It has very good Tensile as well as compressive strength.
2. Ductility
Ductility of structures is increase due to steel reinforcement
3. Durability
R.C. Structures are more durable.
4. Mouldability
The flexibility of reinforcement and the fluidity of concrete makes the R.C. Member to be moulded in any shape. Hence it is suitable for architectural requirement.
5. Permeability
R.C. Members are impermeable to moisture
6. Fire resistance
R.C. Structures are more fire resistance than other materials such as steel and wood.
Disadvantages of R.C.C
R.C.C. Has followed disadvantages
1. Weight of R.C. Structures are more than other materials.
2. Heavy formwork is required for R.C. Members
3. R.C. Structures take more times to attain its full strength.
Reinforced Concrete Building Elements
Main elements of the RC building are Elements of Reinforced Concrete Building
1. Slab
2. Beam
3. Column
4. Footing
Design of each element depends on load on structure and structure action of member subjected to this load.
Load transfer mechanism in R.C. Building is load from slab is transferred to the supporting beams, and from beam to column and from column to footing ultimately, footing transferred the loads to soil strata.
1. Slabs
Slab is the two-dimensional element i.e., plate element because the depth of slab is so smaller than its length in x and y direction. It is a flexural member subject to transverse load.
2. Beams
Beam is the one-dimensional element which is subjected to transverse loading. Beam carries load from slabs, from masonry walls and their self-weights. Beams may be supported on another beam or may be on supported on columns. Failure of beam will be local failure, which may lead to failure of that floor only.
3. Columns
Columns are generally the vertical member subjected to axial or eccentric loads. The load carries by column is comes from beams and from upper columns, if any. The column is very important structural member because failure of column leads to collapse of whole structure.
4. Footings
Footing is the strong base to the structures. It helps to transmit the loads from structure uniformly to the large area beneath.
Key takeaways:
1. Since WSM based on elastic theory, the reserve strength materials beyond yield point is not taken into account.
2. In working stress method, serviceability criteria is not taken into consideration, moment of resistance for same cross section is more in LSM than WSM.
Concrete is strong in compression but weak in tension.
Steel is reinforced suitable at the place where concrete is weak in tension. Such combination of steel and concrete is called as reinforced concrete.
The purpose of R.C. Structure is increase strength of concrete section and to reduce the size of structural members.
Various design philosophies of R.C. Structures are
(i) Working stress method (WSM)
(ii) Ultimate Load method (ULM)
(iii) Limit state method (LSM)
Working Stress Method (WSM)
WSM in one of the oldest methods of design of structures
It is based on the elastic theory. In WSM, a structural element is so designed that the permissible stresses are not exceeded anywhere in the structures when it is subjected to worst combination of working loads.
In WSM, the reserve strength to materials beyond yield point is not taken into account.
The permissible stress in concrete is obtained by the ratio of ultimate strength of concrete to factor of safety.
The permissible stress in steel is obtained by the ratio of yield strength or 0.2 % proof stress of steel to factor of safety. As per IS456, factor of safety of 3 for concrete and 1.78 for yield strength of steel
Ultimate Load Method
In this method, ultimate load is used as a design load.
Working loads are increased by suitable factor to obtain ultimate loads. These factors are called as load factors.
This load factors give the exact margin of safety in terms of load.
Non-linear stress - strain behaviour of concrete is taken into account.
Load factor = Collapse load/ Working load
This theory is based on the assumption that ultimate strain in concrete is 0.3% and the compressive stress at the edge of the section correspond to this strain.
The ULM is most economical than WSM as the section designed by ultimate load methods are thinner and required less reinforcement.
The main drawback of this method is follows
(i) Very thin section obtained by this method leads to excessive deformations and cracking, thus the structure became unserviceable.
(ii) No factor of safety is used for material stresses.
As the serviceability requirement is not satisfied by this method, it was not adopted by structural designers.
Ultimate load method is replaced by Limit state method which takes care of state of collapse and serviceability.
Key takeaways:
(i) Very thin section obtained by this method leads to excessive deformations and cracking, thus the structure became unserviceable.
(ii) No factor of safety is used for material stresses.
Design of contributors and systems of bolstered concrete is a hassle wonderful from however closely associated with analysis. Strictly speaking, it's far nearly not possible to precisely examine a concrete structure, and to layout precisely isn't any much less difficult. Fortunately, we will make some fundamental assumptions which make the layout of bolstered concrete pretty simple, if now no longer easy. A hassle particular to the layout of bolstered concrete systems is the want to element every member throughout. Steel systems, in general, require most effective the specified layout of connections. For concrete systems, we have to decide now no longer most effective the location of longitudinal and lateral reinforcement required in every member, however additionally the manner to pleasant set up and join the reinforcement to insure desirable structural overall performance.
This process may be made fairly simple, if now no longer easy. Purpose of this route is to set up a company expertise of conduct of bolstered concrete systems, then to broaden approach utilized in cutting-edge exercise and to reap familiarity with codes and specs governing sensible layout. In this route we are able to learn how to recognize the simple overall performance of concrete and metal as structural substances, and the conduct of bolstered concrete contributors and systems. If we recognize the simple ideas at the back of code provisions for layout, we are able to have the ability to:
Approach the layout in a greater informed fashion, now no longer like following a black box; and understand and adapt the adjustments in code provisions higher and faster. The ordinary aim is in an effort to layout bolstered concrete systems that are:
Safe
Economical
Efficient Reinforced concrete is one of the predominant constructing substances utilized in engineered systems because:
Low cost
Weathering and hearth place resistance
Good compressive strength
Formability most of these standards make concrete an appealing cloth for huge variety of structural applications consisting of buildings, dams, reservoirs, tanks, etc.
Strength Design (or Ultimate Strength Design)
Select concrete dimensions and reinforcements in order that the member power is ok to face up to forces due to sure hypothetical overload stages, considerably above masses predicted truly to arise in provider. The layout idea is recognized as “power layout.” Based on power layout the nominal power of a member ought to be calculated on the idea of inelastic conduct of fabric. In other words, each reinforcing metallic and urban behave in elastically at final power condition. The power layout technique can be expressed with the aid of using the following, Strength provide ≥ Strength required to hold factored masses in which the “power provided” including second power is computed according with rules and assumptions of conduct prescribed with the aid of using a constructing code, and the “power required” is that acquired with the aid of using acting a structural evaluation the use of the factored masses.
The layout system is more or less as follows: Multiply the running masses with the aid of using the burden component to reap the failure masses. Determine the cross-sectional homes had to face up to failure below those masses. (A member with those homes is stated to have enough power, and could be at the verge of failure while subjected to the factored masses.)
Proportion your participants which have those homes.
Allowable Stress Design: As a trade to the power layout technique, participants can be proportioned in order that stresses within side the metallic and urban due to ordinary provider masses are within special limits (an allowable, or permissible, strain or load). These limits, recognized as allowable stresses are most effective fractions of the failure stresses of the fabric. Allowable strain layout is likewise mentioned as “running strain layout.” For instance, in layout of metallic structures, this allowable strain can be within side the elastic variety of the fabric and can be much less than the yield strain Fy.
A traditional fee might be 0.60Fy. The allowable strain is acquired with the aid of using dividing both the yield strain Fy or the tensile power Fu with the aid of using a component of safety. This method to layout is likewise called elastic layout or running strain layout. Working stresses are the ones because of the running masses, that are the carried-out masses. A well-designed member can be burdened to no extra than the allowable strain while subjected to running masses.
Examples 1:
Using stress and strain diagrams for a balanced singly reinforced section as per WSM Derive the design constants k= neutral axis constant, j= Lever arm constant and R =moment of resistance constant). Use M20 grade of concrete and Fe 415 grade steel
Solution:
Given:
- Neutral axis constant
Consider equivalent stress diagram, by similarity of triangles
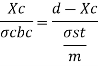
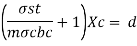
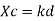
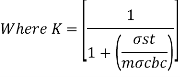
2. Lever arm constant
Lever arm = d-x/3= k-kd/3= (1-k/3)d= jd
Where j = Lever arm constant
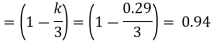
3. Moment of resistance
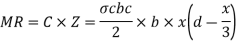
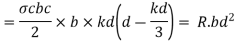
Where r= Lever ram constant =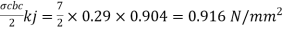 
Type 1: Numerical on moment of resistance and UDL of singly reinforced beam
Given data: Size of beam, area of steel and grade of materials
Step 1: Depth of critical neutral axis Xc
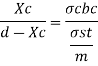
Step 2: Actual depth of neutral axis (x)
Step 3: Types of beam section
1) X= Xc, balanced section
2) X<Xc, under reinforced section
3) X>Xc, over reinforced section
Step 4) Moment of resistance
1) For under reinforced section
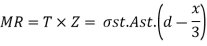
2) For over reinforced section
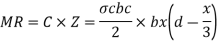
3) For balanced section
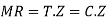
Examples:
A reinforced concrete beam section of size 300mm x 700mm effective depth is reinforced with 3 bars of 20 mm diameter in tension. The concrete mix and HYSD steel reinforcement used are of grade M20 and Fe415 respectively.
Find:
- Depth of neutral axis
- Type of reinforced section
- Moment of resistance
- Maximum stresses induced in the materials W.S.M is recommended.
Solution:
Given: b= 300 mm, d= 700mm
To find:
X, MR and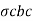 
For M20
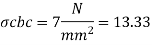
For Fe415
Area of steel in tension
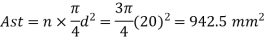
Step 1: Depth of critical neutral axis Xc
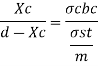
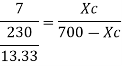
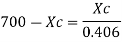
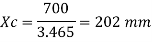
Step 2: Actual depth of neutral axis (x)
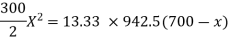
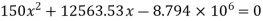
Solving quadratic equation
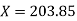
Step 3 Type of beams section
Since X> Xc the section is over reinforced, section and will be falls in compression
Step 4 Moment of resistance
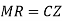
Step 5 Maximum stress in induced in materials
Since the section fails in compression
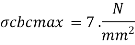
Corresponding maximum stress in steel
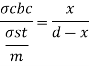
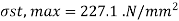
Example 2: A rectangular RCC beam of size 230 mm wide 660 mm effective depth is reinforced with 4 no. 20 mm diameter bars. Find out moment of resistance of beam. Also state weather the beam is under reinforced or over reinforced materials: M30 grade of concrete and HYSD reinforcement of grade Fe 415 W.S.M is recommended.
Solution:
Given:
b=230mm
Effective depth d = 660 mm
To find: MR
For M30
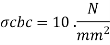
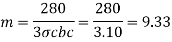
For Fe 415
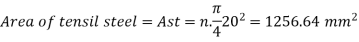
Step 1 Depth of critical neutral axis
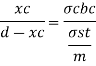
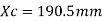
Step 2 Actual depth of neutral axis
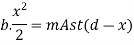
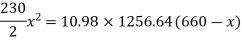
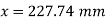
Step 3 Type of section
Since X > Xc the section is over reinforced the beam is fails under compression
Step 4 Moment of resistance
MR= Cz
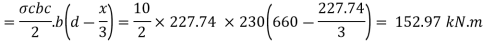
Key takeaways:
Step 1: Depth of critical neutral axis Xc
Step 2: Actual depth of neutral axis (x)
Step 3: Types of beam section
1) X= Xc, balanced section
2) X<Xc, under reinforced section
3) X>Xc, over reinforced section
Step 4: Moment of resistance
1) For under reinforced section
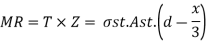
2) For over reinforced section
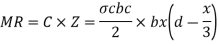
3) For balanced section
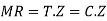
Limit state method is an improved design philosophy to overcome the drawbacks of WSM and ULM.
It is based on semi-empirical approach.
Limit states are the various requirements that a structure is expected to fulfil so that the performance of the structure satisfies the intended purpose for which it is built.
It is the comprehensive method which will take care of both strength and serviceability requirements.
IS456 2000 is used to design the plain and reinforced concrete by this method. It considered limit state for collapse and serviceability.
Limit state of collapse are axial (tension and compression), flexure, shear and torsion.
Limit state of serviceability are deflection, vibration, durability, fire resistance.
Permissible Stresses for Materials in the WSM
As per annex B table 21 and 22 of IS456: 2000 gives the permissible stresses of concrete and steel.
Key takeaways:
IS456 2000 is used to design the plain and reinforced concrete by this method. It considered limit state for collapse and serviceability.
Limit state of collapse are axial (tension and compression), flexure, shear and torsion.
Limit state of serviceability are deflection, vibration, durability, fire resistance.
Limit State
It is the acceptable limit for the safety and serviceability of the structure before failure occurs.
The structure will not become unfit for use and will not reach a limit state.
Types of limit states:
- Limit state collapse
- Limit state of serviceability
Limit State of Collapse
The resistance to bending, shear, torsion and axial loads at every section shall not be less than appropriate value at that section produced by the probable most unfavorable combination of loads on the structure using the appropriate partial safety factors.
Limit State of Serviceability
- Deflection
The final deflection due to all loads including the effect of temperature, creep, shrinkage and measured from the as-cast level of the supports of all horizontal members should not normally span/250.
The deflection including the effect of temperature, creep and shrinkage occurring after erection of partitions and the application of finishes should not normally exceed span/350 or 20 mm whichever is less.
For beams and slabs the vertical deflection limits may generally be assumed to be satisfied provided that the span to depth ratios are not greater than the values obtained as below:
i) For span upto 10 m. Basic L/d ratio
a) cantilever 7
b) simply supported 20
c) continuous 26
Ii) For span above 10 m. Basic L/d ratio x 10/span (except for cantilevers)
b. Cracking
Is 456-2000 Prescribes the following limiting cracks widths in the structural concrete members depending upon the environmental exposure condition:
Sr No | Types of exposure | Permissible width of cracks at surface |
1 | Protected and not exposed to aggressive environmental condition | 0.3mm |
2 | Moderates environmental Condition | 0.2mm |
3 | Aggressive environmental condition | 0.1 mm |
Key takeaways:
- Limit state collapse
- Limit state of serviceability
Shear in Structural Members
The section of a structural member is subjected to shear force due to flexure, punching or torsion. With the shear the span change of bending moment along is called as flexural shear. The beams are usually subjected to flexural shear. The shear developed due to punching action on thin member associated by a concentrated load is called as punching shear.
It occurs in footing slab subjected concentrated load through column, slab carrying a concentrated wall load etc.
The shear induced in the member due to torsion is called as torsion shear.
Shear failure of RCC beam may not lead to immediate failure, it reduces the flexural strength of members and thus it is a state of impeding shear failure.
Shear Stress in Homogenous Beams
The beam subjected to transfers is subjected to shear force and bending moment.
The shear stress induced in the member to resist shear force. As per elastic theory of bending, shear stress distribution across the section is given by equation.
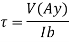
b = Width of the section V = shear force at the section.
Shear stress induced in rectangular section is parabolic in nature with zero at top and bottom and the maximum shear stress at neutral axis.
Shear Stresses in R.C.C. Beams
In reinforced concrete beam, the concrete below the neutral axis is neglected and shear force is resisted by the bound between the steel and concrete.
The shear stress in RC beam is parabolic with zero at top and maximum at neutral axis.
The shear stress below the neutral axis is constant in tensile zone. The shear stress below the neutral axis is constant in tensile zone.
Total shear force in the section V is given by V = Area of stress diagram x breadth of the beam
[Area of parabolic part + area of rectangular part] x breadth of the beam
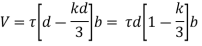
The shear stress occurs along with the flexural stress. The inclined cracking effect due to resultant tension are complex and concrete in tension also contributes in retesting shear upto some extent, hence the evaluation of shear stress is very complex.
In IS 456: 2000, the equation of shear stress is simplified by replacing lever arm factor (jd) by the effective depth, the shear stress obtained is called as nominal shear stress
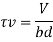
Nominal shear stress in beams of varying depth
- In case of beams of varying depth, the nominal shear stress is calculated by
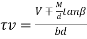ere
M = bending moment at the section B = Angle between the top and bottom edge of the beam
Negative sign is applied when moment M increases numerically in the same direction as effective depth increases and positive sign when M, decreases in this direction. Cantilever beam, continuous beam with haunches at support are the common example of beams with varying depth,
Bond
The bond in RCC is the adhesive force developed between concrete and reinforcing steel to transfer the axial force from a reinforcing bar to the surrounded concrete.
Bond ensures the strain compatibility of RCC
Bond between steel and concrete can be improved due to
(i) Use of rich mix
(ii) Perfect compaction and curing
(iii) Adequate cover to steel
(iv) Use deformed bar
Bond Stresses
The shear stress developed along the contact surface of the reinforced bar and concrete is defined as bond stress.
It is denoted by T
The main function of bond stress to prevent slipping of bar through the harden concrete.
Bars in Tension (cl. 26.2.2.1 of IS456)
Bends and hooks shall conform to IS 2502.
i) Bends
Bends, conforming to standards are frequently resorted to in order to provide anchorage, contributing to the requirements of development length of bars in tension or compression. The Code (Clause 26.2.2.1 b (1)) specifies that "the anchorage value of a bend shall be taken as 4 times the diameter of the bar for each 45° bend, subject to a maximum of 16 times the diameter of the bar".
Commonly a 'standard 90° bend' (anchorage value = 86) is adopted including a minimum extension of 4.
Ii) Hooks
When the bend is turned around 180° (anchorage value = 160) and extended beyond by 40, it is called a standard U-type hook
The minimum (internal) turning radius specified for a hook is 20 for plain mild steel bars and 40 for cold-worked deformed bars. Hooks are generally considered mandatory for plain bars in tension
In the case of stirrup (and transverse tie) reinforcement, the Code (Clause 26.2.2.4b) specifies that complete anchorage shall be deemed to have been provided if any of the following specifications is satisfied:
90° bend around a bar of diameter not less than the stirrup diameter o, with an extension of at least 80: 135° bend with an extension of at least 60;
Examples:
Q.1 A reinforced concrete rectangular beam has a width 230 mm and total depth 600 mm with clear cover 25 mm the beam is reinforced with 3 bars with 16 mm diameter at support section at tension side. Calculate shear strength of support section if 8 mm diameter two legged stirrups are provided at spacing 150mm center to center. Use M20 grade of concrete and Fe 415 grade of steel. Use LSM
Solution:
Given:
b= 230mm
D= 600 mm
Clear cover = 25 mm
Ast= 3-16 mm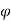
Asv = 8 mm diameter 2 legged stirrups
To find: Shear resistance Vu
Area of steel in tension Ast =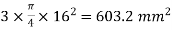 
Area of vertical stirrups Asv
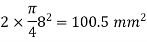
Spacing of stirrups = Sv = 150 mm
Effective depth d = D-C-
= 600-25-16/2 = 567 mm
Step 1 Design shear strength in concrete
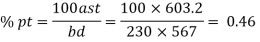
Refer table 19 page no 73 of IS 456-2000
For M20 and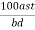 
= 0.46
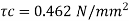
Step 2 Shear capacity of concrete
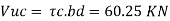
Step 3 Shear resistance by vertical stirrups
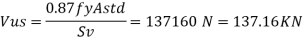
Step 4 Total shear capacity of RC beam
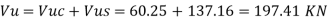
Example 2 A reinforcement concrete rectangular beam has width 230 mm and total depth 550mm with clear cover of 30 mm. The beam is reinforced with the 3 bars with 16 mm diameter at support reaction at tension side. Calculate shear strength of the support reaction if 8 mm diameter two legged stirrups are provided at spacing 175 mm center to center. Use M20 grade of concrete and Fe 415 of steel. Use LSM
Solution:
Given:
b = 230 mm
D= 550 mm
Clear cover = 30 mm
Ast = 3-16 mm
Asv= 8 mm diameter 2 legged stirrups
To find: Shear resistance Vu
Area of steel in tension
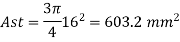
Area of vertical stirrups
Spacing of stirrups Sv= 175 mm
Effective depth
d = D-C-
= 550-30-16/2 = 512 mm
Step 1 Design shear strength in concrete
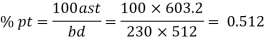
Refer table 19 page no 73 of IS 456-2000
For M20 and 
= 0.512
Step 2 Shear capacity of concrete
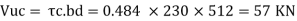
Step 3 Shear resistance by vertical stirrups
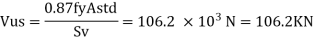
Step 4 Total shear capacity of RC beam
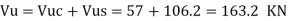
Example 3 A rectangular RCC beam 300 x 700 mm with effective cover 40 mm is subjected to following actions
- Factored BM= 190 KN-m
- Factored SF = 50 KN
- Factored torsion moment = 20 KN-m
Design the beam for flexure and shear using M20 and Fe 415
Solution:
Given:
b = 300 mm
Overall depth D= 700 mm
Effective cover C = 40 mm
Factored BM Mu = 190 KN-m
Factored SF Vu = 50 KN-m
Factored torsion Tu = 20 KN-m
Fck = 20 N/mm^2
Fy = 415 N/mm^2
To find: Reinforcement
Effective depth d = D-c= 700-40 = 600 mm
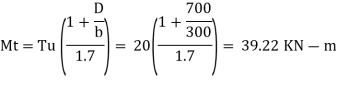
Mt < Mu only tension reinforcement designed, there is no need a compression reinforcement due the twisting moment.
Equivalent moment
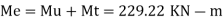
Limiting moment of resistance for Fe415
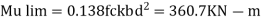
Since Mue< Mu lim the section is designed as a singly reinforced beam
Area of tensile steel
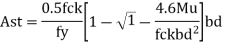
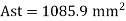
Number of bars
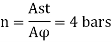
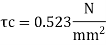
Maximum shear stress
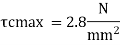
Shear capacity of concrete
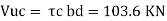
Shear capacity of steel reinforcement
Use double legged 6 mm vertical stirrups
Asv = 
Spacing for stirrups
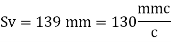
Provide 6 mm -1 legged vertical stirrups @130 mm c/c
Key takeaways:
Design steps:
Shear resistance Vu
Area of steel in tension Ast
Area of vertical stirrups Asv
Spacing of stirrups
Effective depth d = D-C-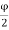
Step 1 Design shear strength in concrete
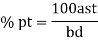
Step 2 Shear capacity of concrete
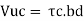
Step 3 Shear resistance by vertical stirrups
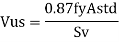
Step 4 Total shear capacity of RC beam
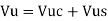
Case study:
- Limit state method
Limit state method is an improved design philosophy to overcome the drawbacks of WSM and ULM.
It is based on semi-empirical approach.
Limit states are the various requirements that a structure is expected to fulfil so that the performance of the structure satisfies the intended purpose for which it is built.
It is the comprehensive method which will take care of both strength and serviceability requirements.
IS456 2000 is used to design the plain and reinforced concrete by this method. It considered limit state for collapse and serviceability.
Limit state of collapse are axial (tension and compression), flexure, shear and torsion.
Limit state of serviceability are deflection, vibration, durability, fire resistance.
Permissible Stresses for Materials in the WSM
As per annex B table 21 and 22 of IS456: 2000 gives the permissible stresses of concrete and steel.
B. Limit state of collapse and limit state of serviceability
Limit State
It is the acceptable limit for the safety and serviceability of the structure before failure occurs.
The structure will not become unfit for use and will not reach a limit state.
Types of limit states:
3. Limit state collapse
4. Limit state of serviceability
Limit State of Collapse
The resistance to bending, shear, torsion and axial loads at every section shall not be less than appropriate value at that section produced by the probable most unfavorable combination of loads on the structure using the appropriate partial safety factors.
Limit State of Serviceability
- Deflection
The final deflection due to all loads including the effect of temperature, creep, shrinkage and measured from the as-cast level of the supports of all horizontal members should not normally span/250.
The deflection including the effect of temperature, creep and shrinkage occurring after erection of partitions and the application of finishes should not normally exceed span/350 or 20 mm whichever is less.
For beams and slabs the vertical deflection limits may generally be assumed to be satisfied provided that the span to depth ratios are not greater than the values obtained as below:
i) For span upto 10 m. Basic L/d ratio
a) cantilever 7
b) simply supported 20
c) continuous 26
Ii) For span above 10 m. Basic L/d ratio x 10/span (except for cantilevers)
b. Cracking
Is 456-2000 Prescribes the following limiting cracks widths in the structural concrete members depending upon the environmental exposure condition:
Sr No | Types of exposure | Permissible width of cracks at surface |
1 | Protected and not exposed to aggressive environmental condition | 0.3mm |
2 | Moderates environmental Condition | 0.2mm |
3 | Aggressive environmental condition | 0.1 mm |
