Unit - 2
Numerical differentiation, integration and solution of differential equations
Formulae for derivatives:
Newton’s forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.
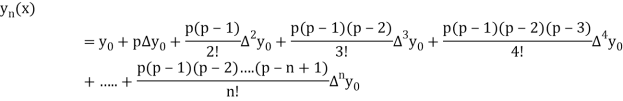
Where 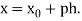
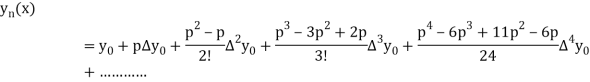
Differentiating both side with respect to p, we get
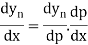
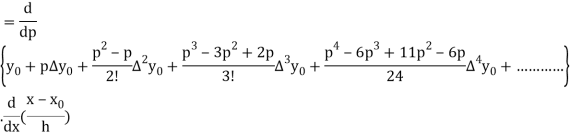
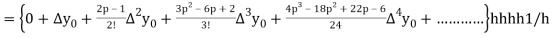 h
h
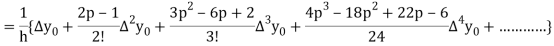
This formula is applicable to compute the value of 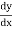 for non tabular values of x.
for non tabular values of x.
For tabular values of x , we can get formula by putting 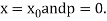
Therefore
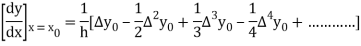
In similar manner we can get the formula for higher order by differentiating the previous order formulas
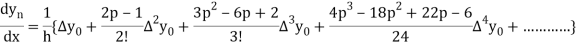
Again, differentiating with respect to p, we get
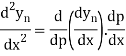
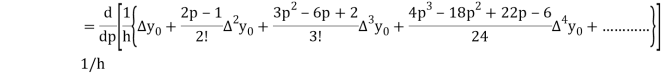
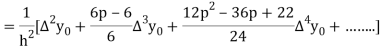
Hence
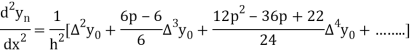
Also
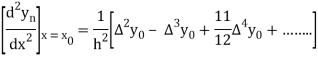
And so on.
Example1: Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find 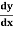 at
at 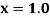 .
.
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y | 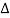 | 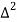 | 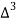 |
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
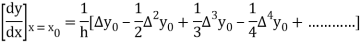
Here 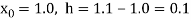
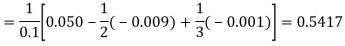
Example2: Find the first and second derivatives of the function given below at the point 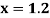 :
:
X | 1 | 2 | 3 | 4 | 5 |
Y | 0 | 1 | 5 | 6 | 8 |
Here the point of the calculation 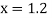 is at the beginning of the table,
is at the beginning of the table,
Forward difference table is given by:
X | Y | 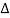 | 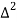 | 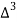 | 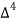 |
1
2
3
4
5 | 0
1
5
6
8 |
1
4
1
2 |
3
-3
1 |
-6
4
|
-10
|
By Newton’s forward differentiation formula for differentiation
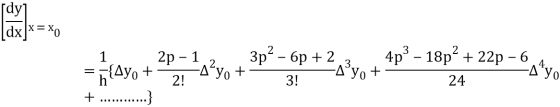
Here  ,
, 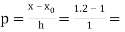 0.
0.
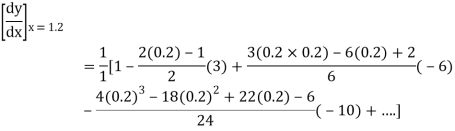
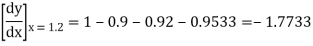
Again
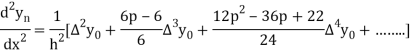
At 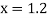
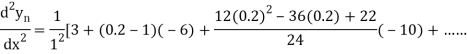
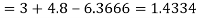
Example3: From the following table of values of x and y find 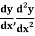 for
for 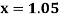
X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
Y | 1.0000 | 1.02470 | 1.04881 | 1.07238 | 1.09544 | 1.11803 | 1.14017 |
Here the value of the derivative is to be calculated at the beginning of the table.
Forward difference table is given by
X | Y | 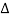 | 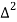 | 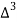 | 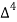 | 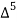 | 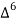 |
1.00
1.05
1.10
1.15
1.20
1.25
1.30 | 1.0000
1.02470
1.04881
1.07238
1.09544
1.11803
1.14017 |
0.02470
0.02411
0.02357
0.02306
0.02259
0.02214 |
-0.00059
-0.00054
-0.00051
-0.00047
-0.00045 |
0.00005
0.00003
0.00004
0.00002 |
-0.00002
0.00001
-0.00002 |
0.00003
-0.00003 |
-0.00006 |
From Newton’s forward difference formula for differentiation, we get
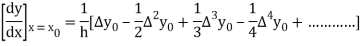
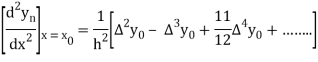
Here 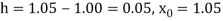
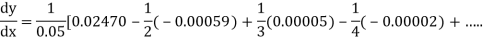
=0.48763
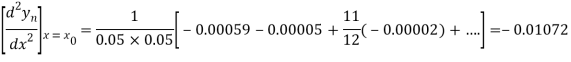
Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
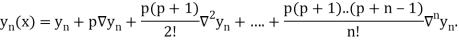
Where 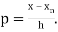
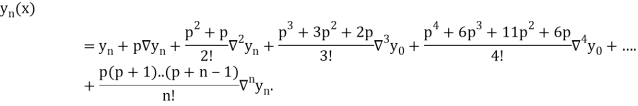
Differentiating both side with respect to p, we get
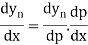
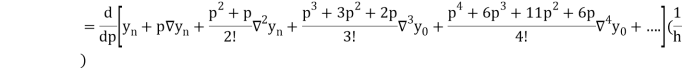
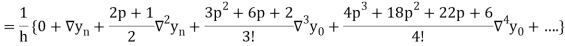
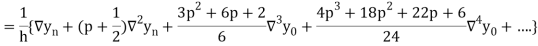
This formula is applicable to compute the value of 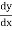 for non tabular values of x.
for non tabular values of x.
For tabular values of x, we can get formula by putting 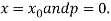
Therefore
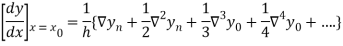
In similar manner we can get the formula for higher order by differentiating the previous order formulas
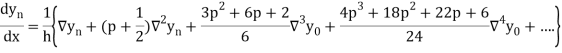
Differentiating both side with respect to p, we get
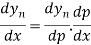
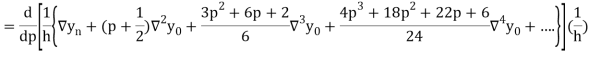
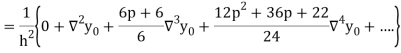
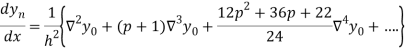
Also
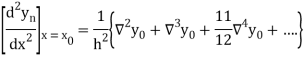
Example1: Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find 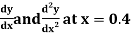 ?
?
Backward difference table:
X | Y | 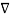 | 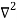 | 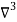 |
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
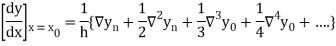
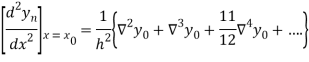
Here 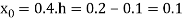
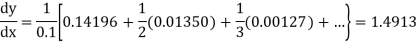
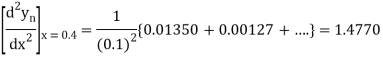
Example2: Given that
X | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
Y | 0 | 0.128 | 0.544 | 1.296 | 2.432 | 4.0 |
Find the derivative of y at 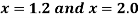 ?
?
The difference table is given below:
X | Y | 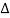 | 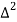 | 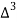 | 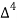 |
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.0 |
0.128
0.416
0.752
0.136
1.568
|
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Since the point 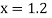 is at the beginning of the table therefore
is at the beginning of the table therefore
From Newton’s forward difference formula for differentiation, we get
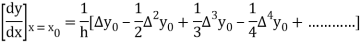
Here 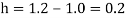
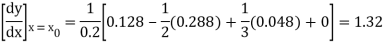
Since the point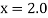 is at the end of the table therefore
is at the end of the table therefore
Backward difference table is:
X | Y |  | 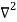 | 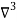 | 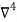 |
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.000 |
0.128
0.416
0.752
0.136
1.568 |
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Newton’s Backward formula for differentiation
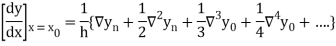
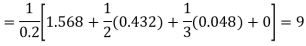
Key takeaways-
Newton’s forward Difference formula:
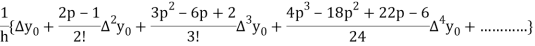
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral 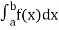 from a set of numerical values of the integrand f(x). In case of function of single variable, the process is called quadrature.
from a set of numerical values of the integrand f(x). In case of function of single variable, the process is called quadrature.
Trapezoidal Method:
Let the interval [a, b] be divided into n equal intervals such that 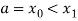 <
<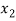 <…. <
<…. <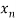 =b.
=b.
Here 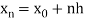 .
.
To find the value of 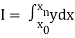 .
.
Setting n=1, we get
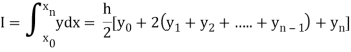
Or I = 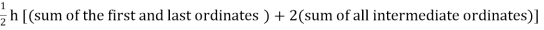
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x), is replaced by n straight lines with the points 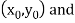 (
(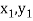 );(
);(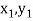 ) and (
) and (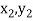 );…….;(
);…….;(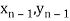 ) and (
) and (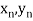 ).
).
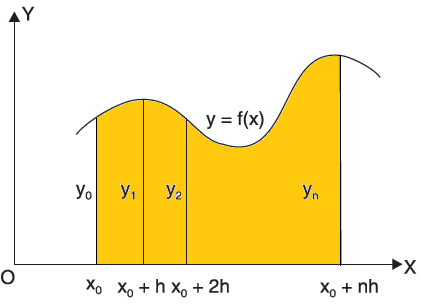
The area bounded by the curve y=f(x), the ordinates 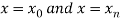 ,and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
,and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
(0, 23), (0.5, 19), (1.0, 14), (1.5, 11), (2.0, 12.5), (2.5, 16), (3.0, 19), (3.5, 20), (4.0, 20).
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =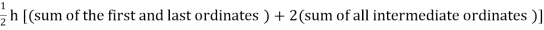
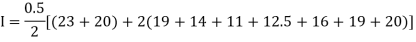
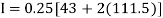
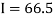
Example2: Compute the value of 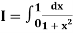
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 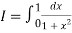
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
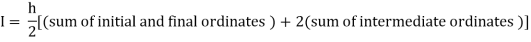
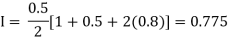
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
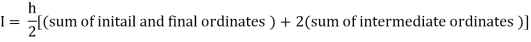
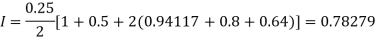
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
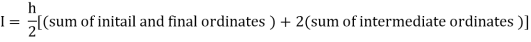
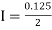 [(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
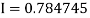
Example3: Evaluate using trapezoidal rule with five ordinates
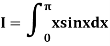
Here 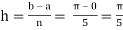
We construct the data table:
X | 0 |  | 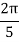 | 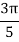 | 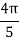 | 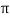 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
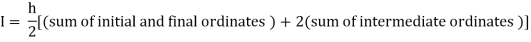
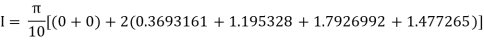
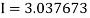
Key takeaways
- Numerical integration is a process of evaluating or obtaining a definite integral
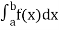 from a set of numerical values of the integrand f(x).
from a set of numerical values of the integrand f(x). 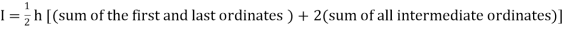
Overview-
Generally fundamental theorem of calculus is used find the solution for definite integrals, but sometime integration becomes too hard to evaluate, numerical methods are used to find the approximated value of the integral.
Simpson’s rules are very useful in numerical integration to evaluate such integrals.
Here we will understand the concept of Simpson’s rule and evaluate integrals by using numerical technique of integration.
We find more accurate value of the integration by using Simpson’s rule than other methods
Simpson’s rule
We will study about Simpson’s one-third rule and Simpson’s three-eight rules.
But in order to get these two formulas, we should have to know about the general quadrature formula-
General quadrature formula-
The general quadrature formula is gives as-
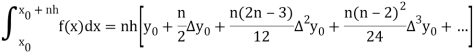
Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.
Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.
Simpson’s one-third rule-
Put n = 2 in general quadrature formula-
We get-
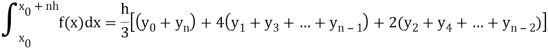
Note- the given interval of integration has to be divided into an even number of sub-intervals.
Simpson’s three-eighth rule-
Put n = 3 in general quadrature formula-
We get-
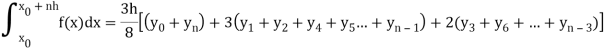
Note- the given interval of integration has to be divided into sub-intervals whose number n is a multiple of 3.
Example: Evaluate the following integral by using Simpson’s 1/3rd and 3/8th rule.
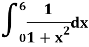
Solution-
First, we will divide the interval into six parts, where width (h) = 1, the value of f(x) is given in the table below-
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
f(x) | 1 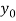 | 0.5 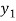 | 0.2 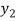 | 0.1 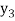 | 1/17 = 0.05884 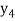 | 1/26 = 0.0385 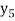 | 1/37 = 0.027 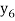 |
Now using Simpson’s 1/3rd rule-
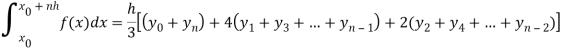
We get-
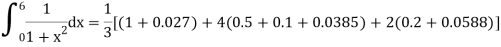
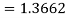
And now
Now using Simpson’s 3/8th rule-
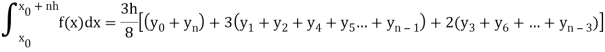
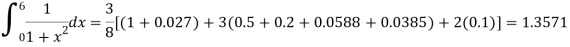
Example: Find the approximated value of the following integral by using Simpson’1/3rd rule.
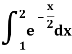
Solution-
The table of the values-
x | 1 | 1.25 | 1.5 | 1.75 | 2 |
f(x) | 0.60653 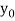 | 0.53526 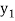 | 0.47237 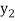 | 0.41686 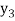 | 0.36788 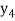 |
Now using Simpson’s 1/3rd rule-
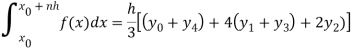
We get-

Example1: Estimate the value of the integral
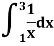
By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 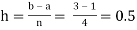
E construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
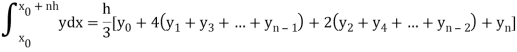
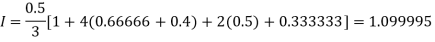
For n = 8, we have 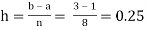
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
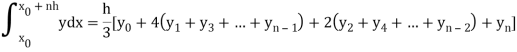
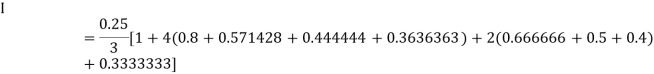
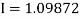
Example2: Evaluate 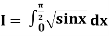 Using Simpson’s 1/3 rule with
Using Simpson’s 1/3 rule with 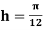 .
.
For 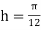 , we construct the data table:
, we construct the data table:
X | 0 | 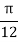 |  |  |  | 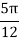 |  |
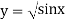 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
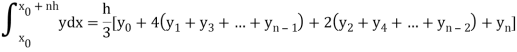
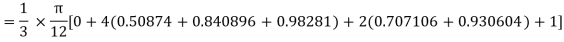
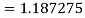
Example3: Using Simpson’s 1/3 rule with h = 1, evaluate
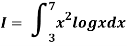
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
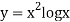 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
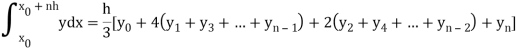
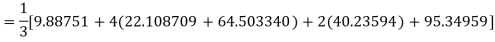
= 177.3853
Example1: Evaluate 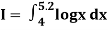
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
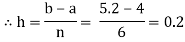
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4. 4 | 4.6 | 4.8 | 5.0 | 5.2 |
Y=logx | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
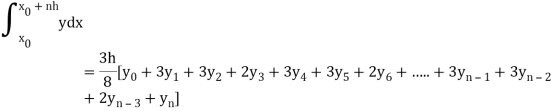

= 1.8278475
Example2: Evaluate 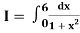
Let us divide the range of the interval [0,6] into six equal parts.
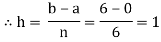
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
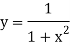 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
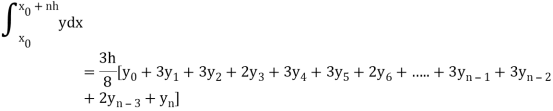
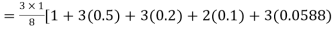 +3(0.0385) +0.027]
+3(0.0385) +0.027]
=1.3571
Error in Integration
Error in Trapezoidal method
The total error in trapezoidal method is given by
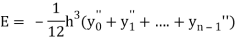
Let 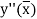 is the largest value of the n quantities on the right-hand side of the above equation then
is the largest value of the n quantities on the right-hand side of the above equation then
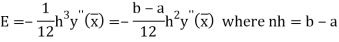
Error in Simpson’s Rule
The error in the Simpson’s rule is given by
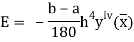
Where 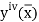 is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by
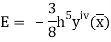
Where 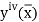 is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Key takeaways
- The general quadrature formula is gives as-
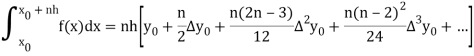
2. Simpson’s one-third rule-
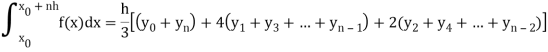
3. Simpson’s three-eighth rule-
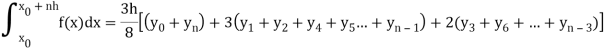
Quadrature: It is the process to evaluate the value of the functions at the chosen point, to its exact value for polynomial up to higher degree as possible.
The general form Gaussian quadrature is given by
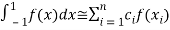
Where 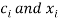 depends on the choice of n (number of points).
depends on the choice of n (number of points).
Also note that the possible polynomial of degree up to 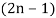 .
.
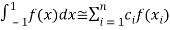
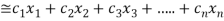 . …... (1)
. …... (1)
For 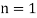 point
point
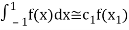
Which gives exact value of the polynomial up to degree  degree
degree
i.e., 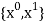
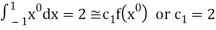
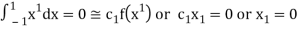
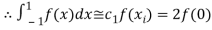
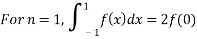
For 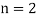 point and using (1)
point and using (1)
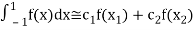
Which gives exact value of the polynomial up to degree  degree
degree
i.e., 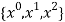
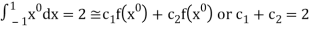
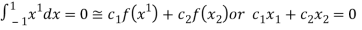
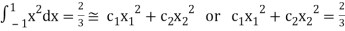
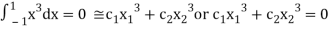
On solving we get
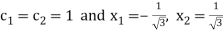 .
.
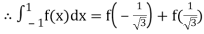
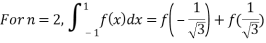
Gauss Quadrature 3-point method:
The general form Gaussian quadrature is given by
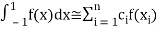
Where 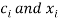 depends on the choice of n (number of points).
depends on the choice of n (number of points).
Also note that the possible polynomial of degree up to 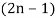 .
.
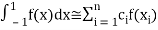
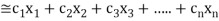 . …... (1)
. …... (1)
For 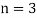 point
point
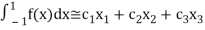
Which gives exact value of the polynomial up to degree  degree
degree
i.e., 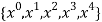
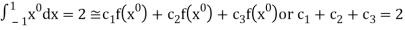
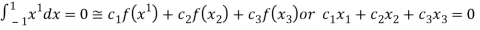
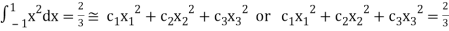
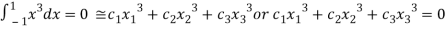
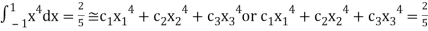
On solving we get
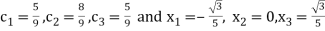 .
.
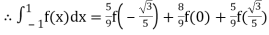
For n=3, 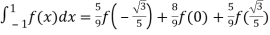
Note: To evaluate 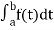
The above integral can be converted into Gauss quadrature by substituting
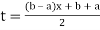
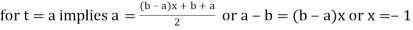
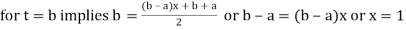
Hence 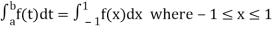 .
.
Example: Evaluate 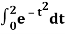
Here 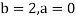
Using 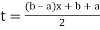 =
=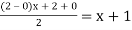
Also 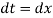
For 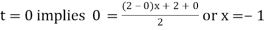
For 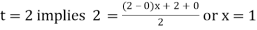
Hence 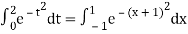
Here 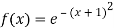
By Gauss quadrature 3-point rule
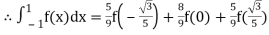
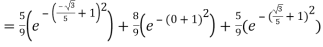
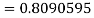
Example: Evaluate 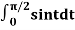 by 2-point Gaussian rule.
by 2-point Gaussian rule.
Here 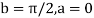
Using 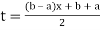 =
=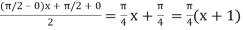
Also 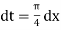
For 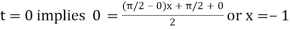
For 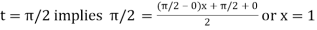
Hence 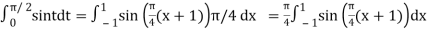
Here 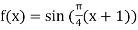
By Gauss quadrature 2-point rule
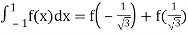
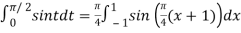
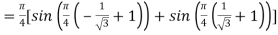
=0.99847
Example: Solve by Gauss quadrature 3-point method 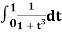
Given 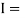
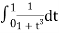
Here 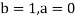
Using 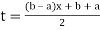 =
=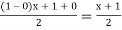
Also 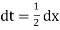
For 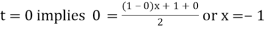
For 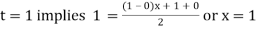
Hence 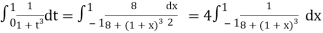
Here 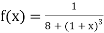
By Gauss quadrature 3-point rule
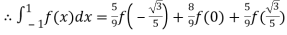
Hence 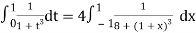
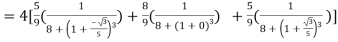
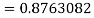
The general first order differential equation
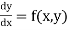 …. (1)
…. (1)
With the initial condition 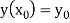 … (2)
… (2)
In general, the solution of first order differential equation in one of the two forms:
a) A series for y in terms of power of x, from which the value of y can be obtained by direct solution.
b) A set of tabulated values of x and y.
The case (a) is solved by Taylor’s Series or Picard method whereas case (b) is solved by Euler’s, Runge Kutta Methods etc.
Euler’s method:
In this method the solution is in the form of a tabulated values
Integrating both side of the equation (i) we get
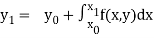
Assuming that 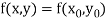 in
in 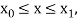 this gives Euler’s formula
this gives Euler’s formula
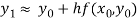
In general formula
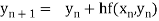 , n=0,1, 2...
, n=0,1, 2...
Error estimate for the Euler’s method
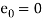
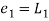
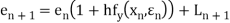
Example1: Use Euler’s method to find y (0.4) from the differential equation
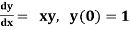 with h=0.1
with h=0.1
Given equation 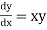
Here 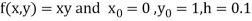
We break the interval in four steps.
So that 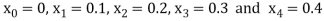
By Euler’s formula
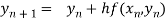 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
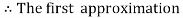
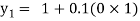
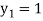
For n=1 in equation (i) we get
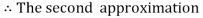
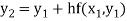
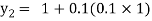
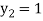 .01
.01
For n=2 in equation (i) we get
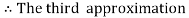
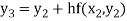
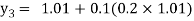
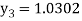
For n=3 in equation (i) we get
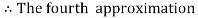
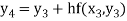
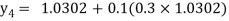
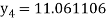
Hence y (0.4) =1.061106.
Example2: Using Euler’s method solve the differential equation for y at x=1 in five steps
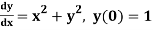
Given equation 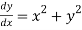
Here 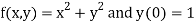
No. Of steps n=5 and so that 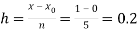
So that 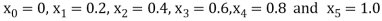
Also 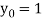
By Euler’s formula
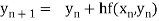 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
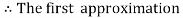
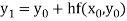
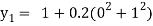
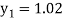
For n=1 in equation (i) we get
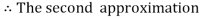
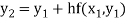
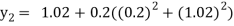
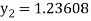
For n=2 in equation (i) we get
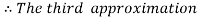
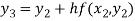
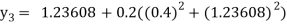
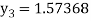
For n=3 in equation (i) we get
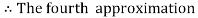
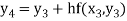
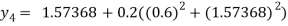
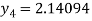
For n=4 in equation (i) we get
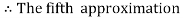
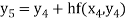
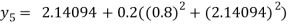
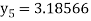
Hence 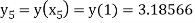
Example3: Given 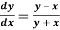 with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
Given equation is 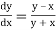
Here 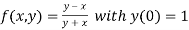
No. Of steps n=5 and so that 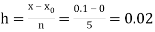
So that 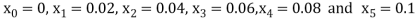
Also 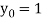
By Euler’s formula
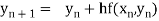 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
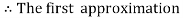
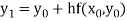
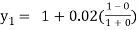
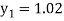
For n=1 in equation (i) we get
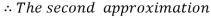
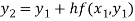
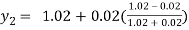
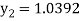
For n=2 in equation (i) we get
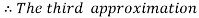
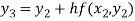
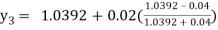
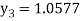
For n=3 in equation (i) we get
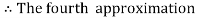
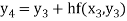
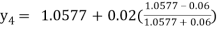
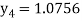
For n=4 in equation (i) we get
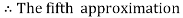
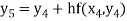
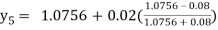
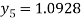
Hence 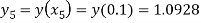
Key takeaways
Euler’s method: 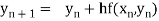 , n=0,1, 2…...
, n=0,1, 2…...
Modified Euler’s Method:
Instead of approximating 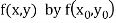 as in Euler’s method. In the modified Euler’s method, we have the iteration formula
as in Euler’s method. In the modified Euler’s method, we have the iteration formula
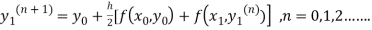
Where 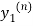 is the nth approximation to
is the nth approximation to 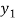 .The iteration started with the Euler’s formula
.The iteration started with the Euler’s formula
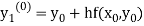
Example1: Use modified Euler’s method to compute y for x=0.05. Given that

Result correct to three decimal places.
Given equation 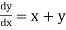
Here 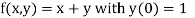
Take h = 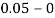 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
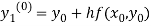
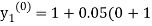 )
)
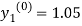
The iteration formula by modified Euler’s method is
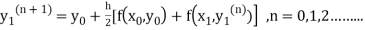 -----(i)
-----(i)
For n=0 in equation (i) we get
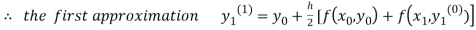
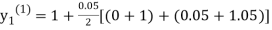
Where 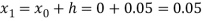 and
and 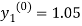 as above
as above
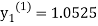
For n=1 in equation (i) we get
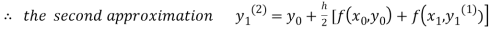
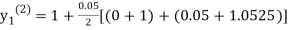
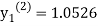
For n=3 in equation (i) we get
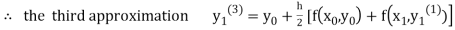
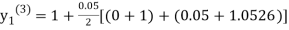
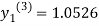
Since third and fourth approximation are equal.
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Example2: Using modified Euler’s method, obtain a solution of the equation
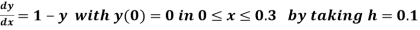
Given equation 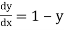
Here 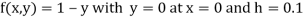
By modified Euler’s formula the initial iteration is
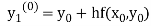
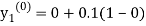
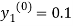
The iteration formula by modified Euler’s method is
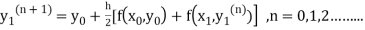 -----(i)
-----(i)
For n=0 in equation (i) we get
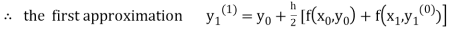
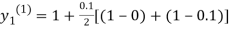
Where 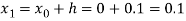 and
and 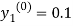 as above
as above
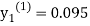
For n=1 in equation (i) we get
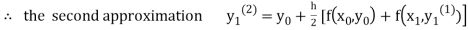
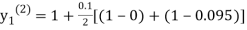
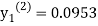
For n=2 in equation (i) we get
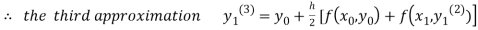
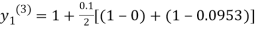
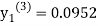
For n=3 in equation (i) we get
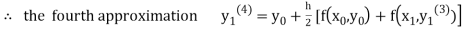
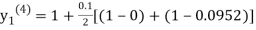
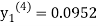
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of 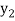 at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
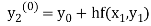
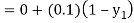
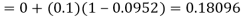
The iteration formula by modified Euler’s method is
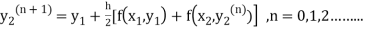 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
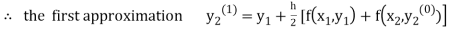
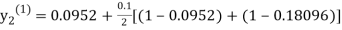
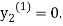 1814
1814
For n=1 in equation (ii) we get
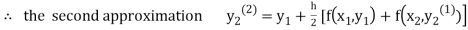
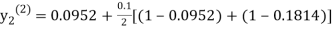
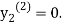 1814
1814
Since first and second approximation are equal.
Hence y = 0.1814 at x=0.2
To calculate the value of 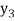 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
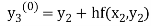
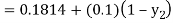
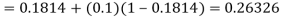
The iteration formula by modified Euler’s method is
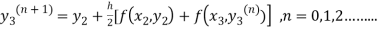 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
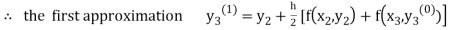
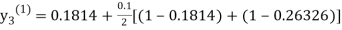
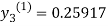
For n=1 in equation (iii) we get
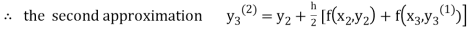
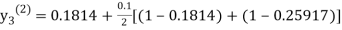
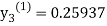
For n=2 in equation (iii) we get
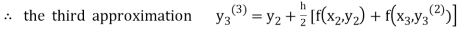
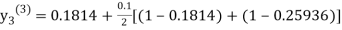
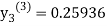
For n=3 in equation (iii) we get
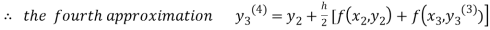
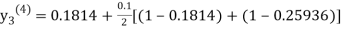
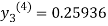
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Key takeaways
Modified Euler’s Method:
Solution of Second order ODE using 4th order Runge-Kutta method (Numerical), Runge-Kutta fourth order method (Numerical)
This method is more accurate than Euler’s method.
Consider the differential equation of first order
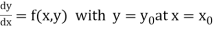
Let 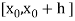 be the first interval.
be the first interval.
A second order Runge Kutta formula
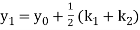
Where 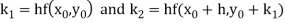
Rewrite as
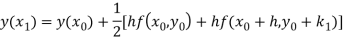
A fourth order Runge Kutta formula:
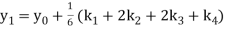
Where 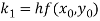
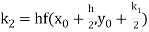
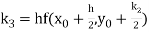
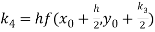
Example1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
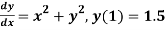
Given equation 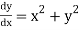
Here 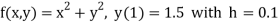
Also 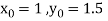
By Runge Kutta formula for first interval
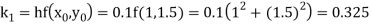
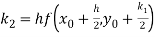
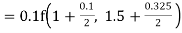
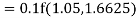
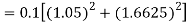
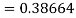
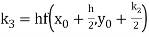
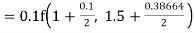
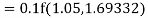
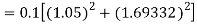
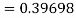
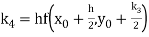
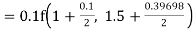
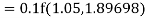
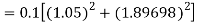
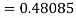
Again 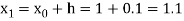
A fourth order Runge Kutta formula:
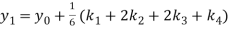
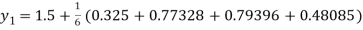
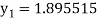
To find y at 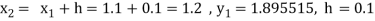
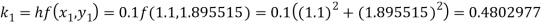
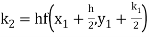
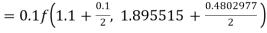
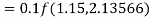
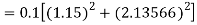
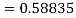
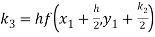
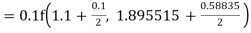
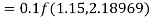
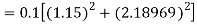
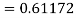
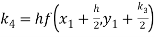
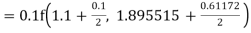
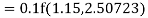
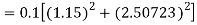
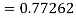
A fourth order Runge Kutta formula:
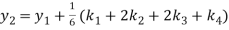
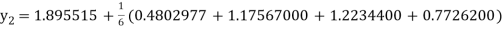
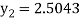
Example2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if
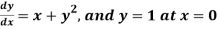
Given equation 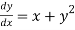
Here 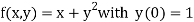
Also 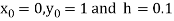
By Runge Kutta formula for first interval
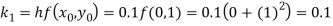
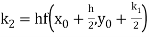
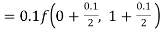
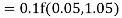
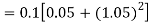
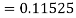
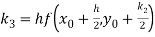
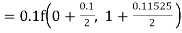
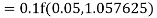
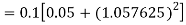
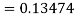
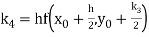
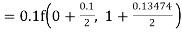
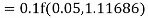
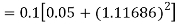
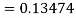
A fourth order Runge Kutta formula:
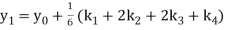
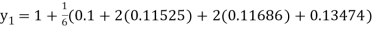
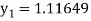
Again 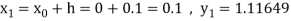
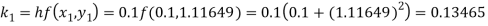
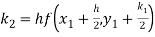
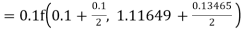
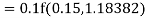
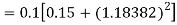
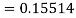

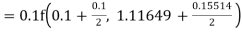
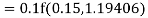
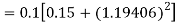
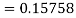
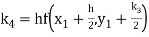
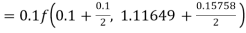
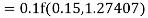
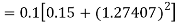
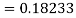
A fourth order Runge Kutta formula:
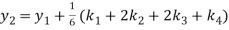
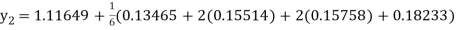
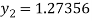
Example3: Using Runge Kutta method of fourth order, solve
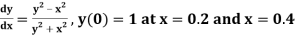
Given equation 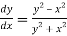
Here 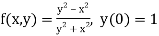
Also 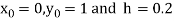
By Runge Kutta formula for first interval
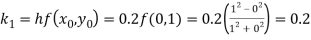
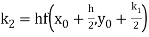
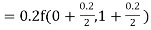
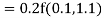
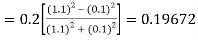
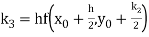
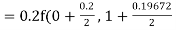 )
)
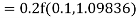
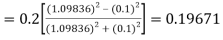
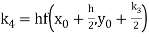
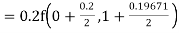
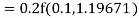
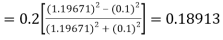
A fourth order Runge Kutta formula:
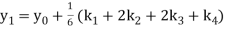
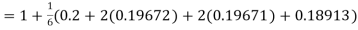
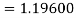
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 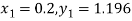
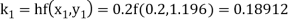
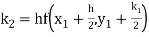
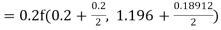
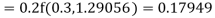
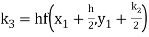
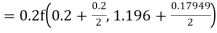
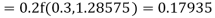
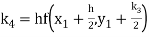
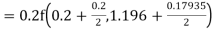
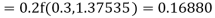
A fourth order Runge Kutta formula:
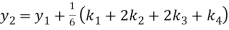
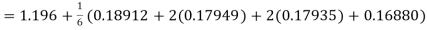
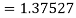
Hence at x = 0.4 then y=1.37527
Solution of Second order ODE using 4th order Runge-Kutta method:
The second order differential equation
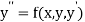
Let 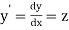 then the above equation reduces to first order simultaneous differential equation
then the above equation reduces to first order simultaneous differential equation
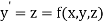
Then 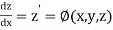
This can be solved as we discuss above by Runge- Kutta Method. Here 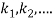 for
for 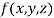 and
and 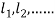 for
for 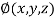 .
.
A fourth order Runge- Kutta formula:
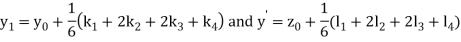
Where 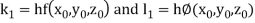
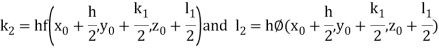
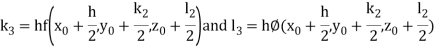
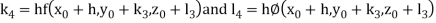
Example1: Using Runge- Kutta method of order four, solve 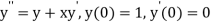 to find
to find 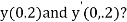
Given second order differential equation is
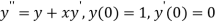
Let 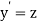 then above equation reduces to
then above equation reduces to
Or 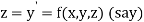
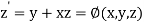 (say)
(say)
Or 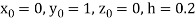 .
.
By Runge- Kutta Method we have
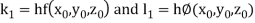
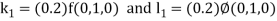
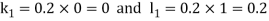
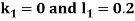
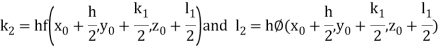
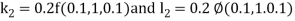
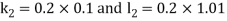
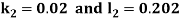
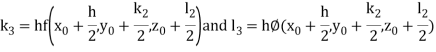
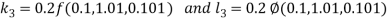
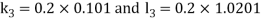
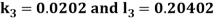
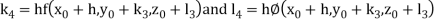
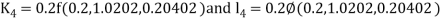
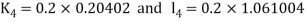
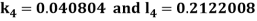
A fourth order Runge Kutta formula:
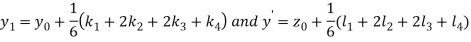
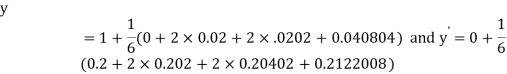
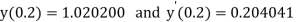
Example2: Using Runge Kutta method, solve
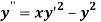 for
for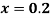 correct to four decimal places with initial condition
correct to four decimal places with initial condition 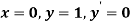 .
.
Given second order differential equation is
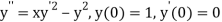
Let 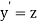 then above equation reduces to
then above equation reduces to
Or 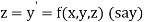
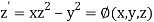 (say)
(say)
Or 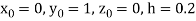 .
.
By Runge-Kutta Method we have
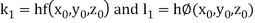
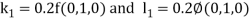
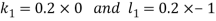
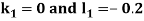
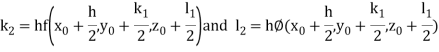
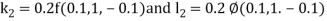
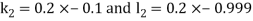
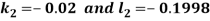
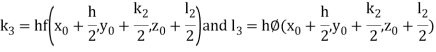
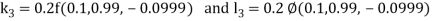
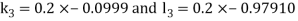
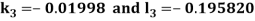
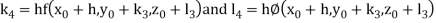
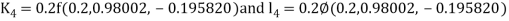
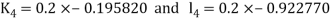
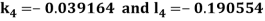
A fourth order Runge Kutta formula:
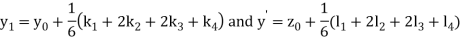
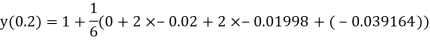
And 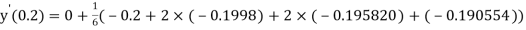
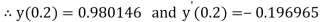 .
.
Example3: Solve the differential equations
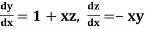 for
for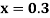
Using four order Runge Kutta method with initial conditions 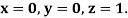
Given differential equation are
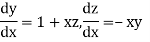
Let 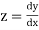
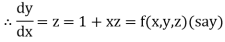
And 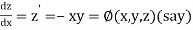
Also 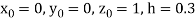
By Runge Kutta Method we have
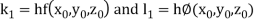
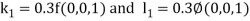
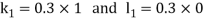

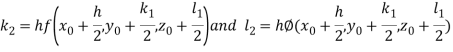
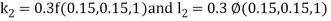
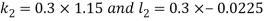
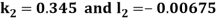
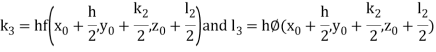
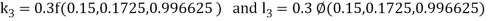
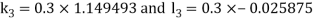
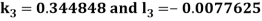
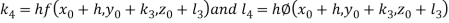
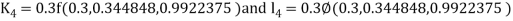
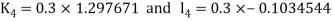
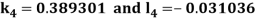
A fourth order Runge Kutta formula:
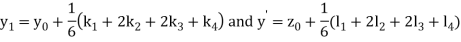
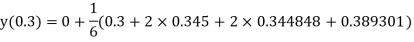
And 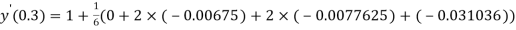
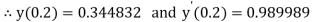 .
.
Key takeaways
A fourth order Runge Kutta formula:
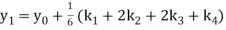
Where 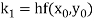
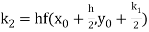
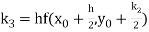
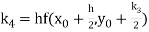
Problems involving second and higher order differential equations, in which the conditions at two or more points are specified, are called boundary-value problems.
Finite difference method
This method is used to solve bounded value problem.
The general two-point linear boundary value problem
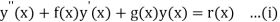
With boundary condition
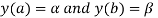
To solve this problem by using finite difference, we divide the interval [a, b] into n sub interval so that 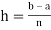 .
.
The approximated function f(x) at the points 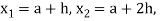
………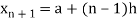
We use the following central difference formula:
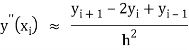
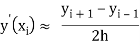
We substitute these value in the given equation and apply the boundary condition to calculate the value of the unknown.
Example1: Solve the boundary value problem defined by
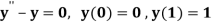
By finite difference method. Compare the solution at y (0.5) by taking h=0.5 and h=0.25.
Given equation 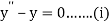
With boundary condition 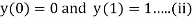
By finite difference method
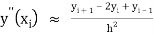 …. (iii)
…. (iii)
Putting(iii) in (i) we get
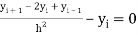 …. (iv)
…. (iv)
For h=0.5, here for  which corresponds to
which corresponds to 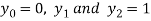
For i=1 in equation (iv) we get
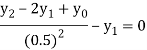
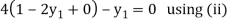
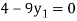
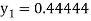
For h=0.25, here 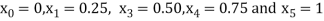
Which corresponds to 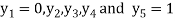
For i=1 in equation (iv) we get
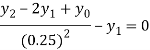
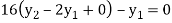
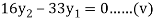
For i=2 in equation (iv) we get
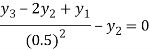
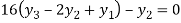
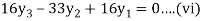
For i=3 in equation (iv) we get
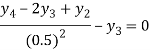
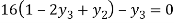
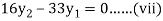
From equation (v), (vi) and (vii) we get
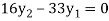
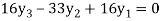
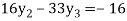
On solving above triangular equation we get
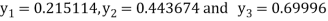
Hence for h=0.5 we get y (0.5) =0.44444
And for h=0.25 we get y (0.5) =0.443674
Example2: Solve the bounded value problem
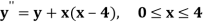
With boundary condition 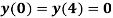
Given equation
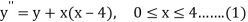
With 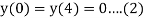
By finite difference method
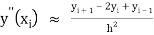 …. (3)
…. (3)
Putting (3) in equation (1) we have
By finite difference method
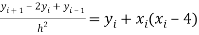 …… (4)
…… (4)
Let h=1, we have 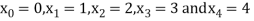
Corresponds to 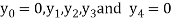
For i=1 in equation (4) we get
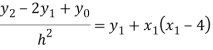
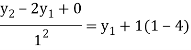
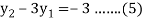
For i=2 in equation (4) we get
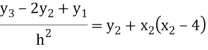
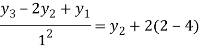
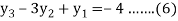
For i=3 in equation (4) we get
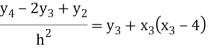
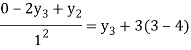
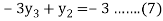
From equation (5), (6) and (7) we get
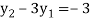
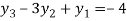
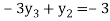
On solving we get 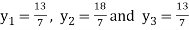
Example3: Solve the boundary value problem
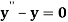
With y (0) =0 and y (2) =3.62686
Given equation 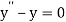 …... (1)
…... (1)
With boundary condition y (0) =0 and y (2) =3.62686…. (2)
By finite difference method
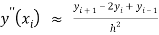 …. (3)
…. (3)
Substituting (3) in equation (1) we get
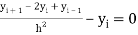 …. (3)
…. (3)
Let h=0.5 then for 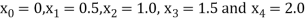
Which corresponds to 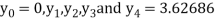
For i=1 in equation (3) we get
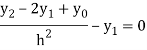
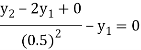
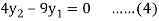
For i=2 in equation (3) we get
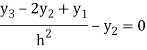
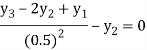
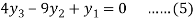
For i=3 in equation (3) we get
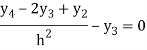
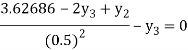
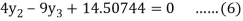
From equation (4), (5) and (6) we get
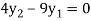
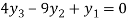
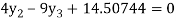
On solving we get 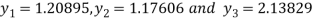
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- Higher engineering mathematics, BV Ramana.
- Computer based numerical & statistical techniques, M goyal