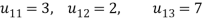Unit - 1
Solution of non-linear, linear equations and interpolation
There are two types of equations Linear and Nonlinear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand, nonlinear equation is those in which y does not directly proportional to x and of degree more than one.
Ex: 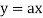 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
 is a non-linear equation.
is a non-linear equation.
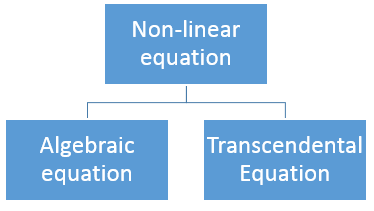
Algebraic Equation:
If f(x) is a pure polynomial, then the equation 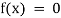 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 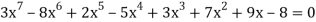
Transcendental Equation:
If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 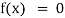 is called transcendental equation.
is called transcendental equation.
Ex 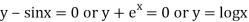
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Bisection method-
This method consists of finding the root of the equation 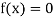 which lies between a and b (say).
which lies between a and b (say).
The function 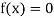 is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is

If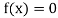 , then the correct root is
, then the correct root is 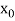 .But if
.But if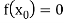 , then the root either lies between a and
, then the root either lies between a and 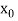 or
or 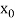 and b according as
and b according as 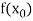 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
Example:
Find a real root of 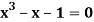 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
Let 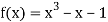 then by hit and trial we have
then by hit and trial we have
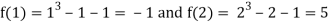
Thus 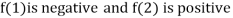 .So the root of the given equation should lie between 1 and 2.
.So the root of the given equation should lie between 1 and 2.

Now, 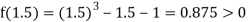
i.e., positive so the root of the given equation must lie between 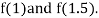

Now, 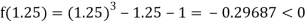
i.e., negative so the root of the given equation lies between 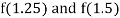

Now, 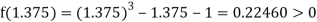
i.e., positive so the root of the given equation lies between 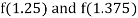
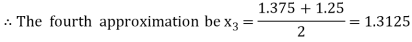
Now, 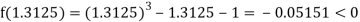
i.e., negative so that the root of the given equation lies between 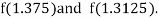
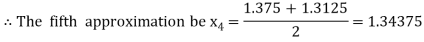
Now, 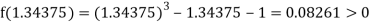
i.e., positive so that the root of the given equation lies between 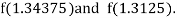
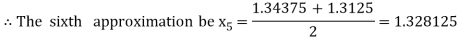
Now, 
i.e., positive so that the root of the given equation lies between 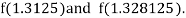
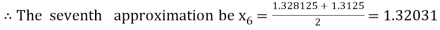
Now, 
i.e. negative so that the root of the given equation lies between 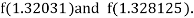

Now, 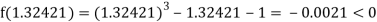
i.e., negative so that the root of the given equation lies between 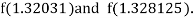
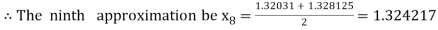
Hence the approximate root of the given equation is 1.32421
Example:
Find the root of the equation , using the bisection method.
, using the bisection method.
Let  then by hit and trial we have
then by hit and trial we have
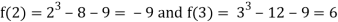
Thus 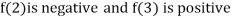 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 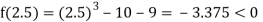
i.e., negative so the root of the given equation must lie between 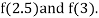

Now, 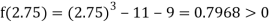
i.e., positive so the root of the given equation must lie between 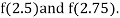

Now, 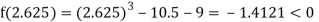
i.e., negative so the root of the given equation must lie between 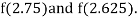
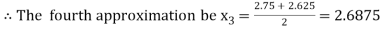
Now, 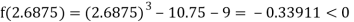
i.e., negative so the root of the given equation must lie between 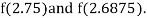
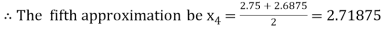
Now, 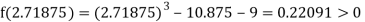
i.e., positive so the root of the given equation must lie between 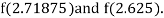

Now, 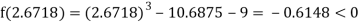
i.e., negative so the root of the given equation must lie between 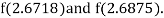
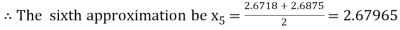
Hence the root of the given equation correct to two decimal place is 2.67965.
Example3
Find the root of the equation 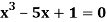 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
Let 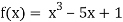
Where 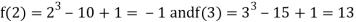
Thus 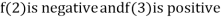 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 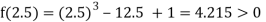
i.e., positive so the root of the given equation must lie between 

Now, 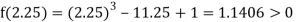
i.e., positive so the root of the given equation must lie between 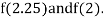

Now, 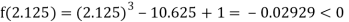
i.e., negative so the root of the given equation must lie between 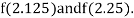

Now, 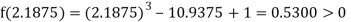
i.e., positive so the root of the given equation must lie between 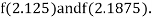
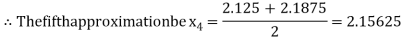
Now, 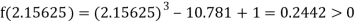
i.e., positive so the root of the given equation must lie between 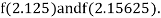
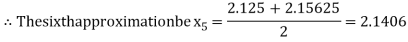
Now, 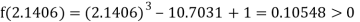
i.e., positive so the root of the given equation must lie between 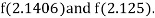
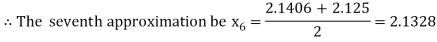
Now, 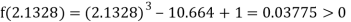
i.e., positive so the root of the given equation must lie between 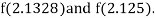
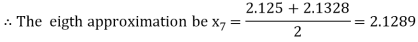
Now, 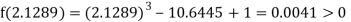
i.e., positive so the root of the given equation must lie between 
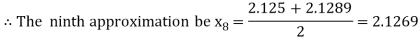
Hence the root of the given equation correct to two decimal place is 2.1269
Key takeaways
- Algebraic Equation- If f(x) is a pure polynomial, then the equation
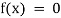 is called an algebraic equation in x.
is called an algebraic equation in x. - Transcendental Equation- If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then
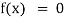 is called transcendental equation.
is called transcendental equation.
Let 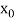 be the approximate root of the equation
be the approximate root of the equation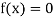 .
.
By Newton Raphson formula 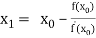
In general
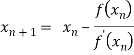
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .
.
Given 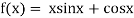
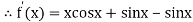
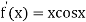
By Newton Raphson Method
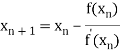
= 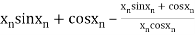
=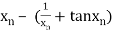
The initial approximation is  in radian.
in radian.
For n =0, the first approximation 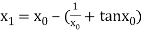
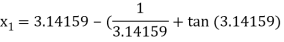
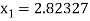
For n =1, the second approximation 
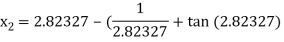
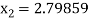
For n =2, the third approximation 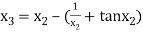


For n =3, the fourth approximation 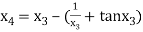
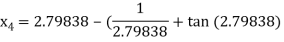
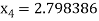
Hence the root of the given equation correct to five decimal place 2.79838.
Example2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 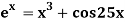 near to 4.5
near to 4.5
Let 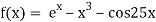
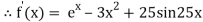
The initial approximation 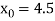
By Newton Raphson Method
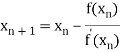
For n =0, the first approximation 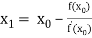

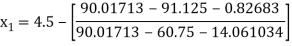
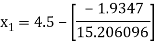
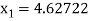
For n =1, the second approximation 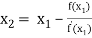

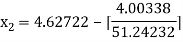
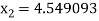
For n =2, the third approximation 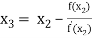

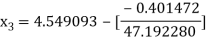
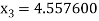
For n =3, the fourth approximation 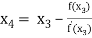


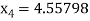
Hence the root of the equation correct to three decimal places is 4.5579
Example3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 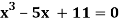
Let 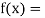
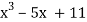
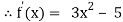
By Newton Raphson Method
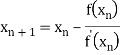
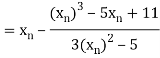

Let the initial approximation be 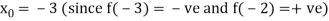
For n=0, the first approximation 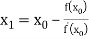
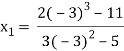
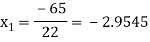
For n=1, the second approximation 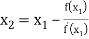
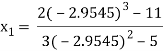
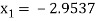
For n=2, the third approximation 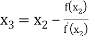
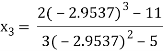

Since 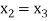 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways
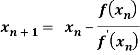
The successive approximation is also known as iteration method. To start the solution using this method we need one or more approximate value which is not necessarily the root of the given equation.
We are finding the root of the given equation
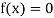 ... (1)
... (1)
We rewrite the given equation in the form
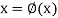 ... (2)
... (2)
We know that the root of the equation lies between its positive and the negative values
Let 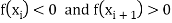
So, the interval of the root of the equation be 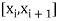 .
.
Now, let 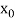 be an approximate root of the given equation (1).
be an approximate root of the given equation (1).
Putting it in equation (2) we get 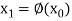
Successive substitution gives the approximations


…………..

If the above values converge to a definite number, then that number will be the root of the given equation.
Example1: Find the real root of the equation
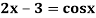
Correct to three decimal places in the interval 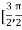 ]
]
The given equation is 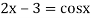 ... (1)
... (1)
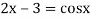
Or 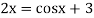
Or 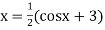 =
= 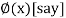 ... (2)
... (2)
Or 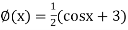
Let 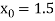 , in the interval
, in the interval 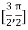 .
.
The successive approximation we have
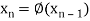
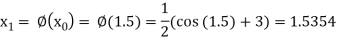

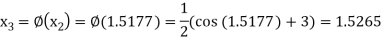

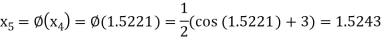
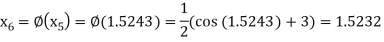

Hence the root of the equation correct to three decimal places is 1.524.
Example: Find the real root of the polynomial 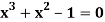 correct to three decimal places?
correct to three decimal places?
Given equation 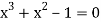 …. (1)
…. (1)
Here 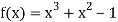
Also 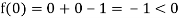
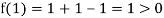
Therefore, root of the equation lies between 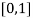 .
.
Again 
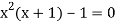
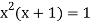
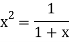
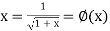 …. (2)
…. (2)
Let 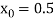 , in the interval
, in the interval  .
.
The successive approximation we have
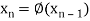
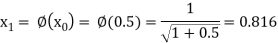
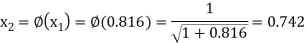
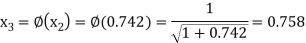

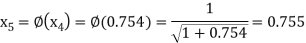
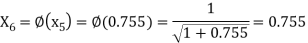
Hence the root of the equation correct to three decimal places is 0.755.
Example3: By iteration method, find the value of 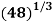 , correct to three decimal places.
, correct to three decimal places.
Let 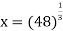
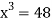
Let 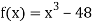 .
.
Also 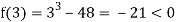

Therefore, the root of the equation lies between 3 and 4.
Given equation can rewrite 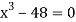 .
.
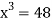
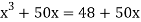

Or  … (2)
… (2)
Let 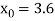 , in the interval
, in the interval 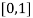 .
.
The successive approximation we have
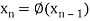
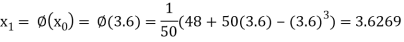

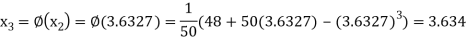
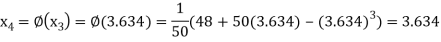
Hence the root of the equation correct to three decimal places is 3.634.
Jacobi’s Iteration method:
Let us consider the system of simultaneous linear equation
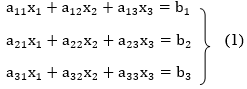
The coefficients of the diagonal elements are larger than the all-other coefficients and are non-zero. Rewrite the above equation we get
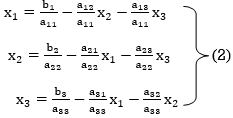
Take the initial approximation  we get the values of the first approximation of
we get the values of the first approximation of .
.
By the successive iteration we will get the desired the result.
Example1 Use Jacobi’s method to solve the system of equations:
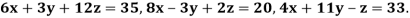
Since 
So, we express the unknown with large coefficient in terms of other coefficients.
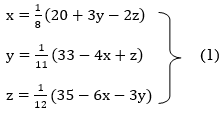
Let the initial approximation be 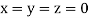
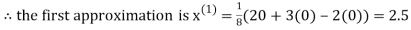
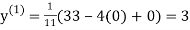

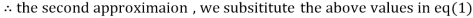
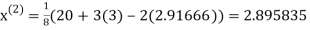
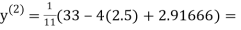 2.35606
2.35606
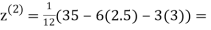 0.91666
0.91666
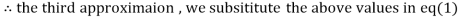
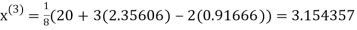


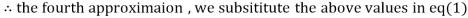
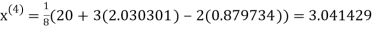
 1.932936
1.932936
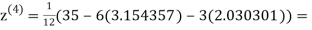 0.831912
0.831912

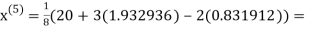 3.016873
3.016873
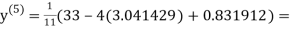 1.969654
1.969654

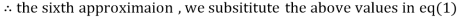
 3.010217
3.010217
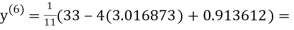 1.986010
1.986010
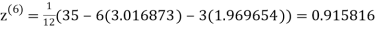

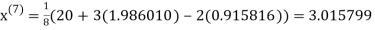
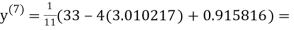 1.988631
1.988631
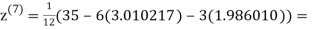 0.915055
0.915055
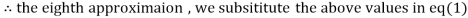
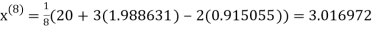
 1.986532
1.986532
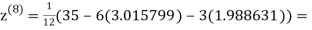 0.911609
0.911609
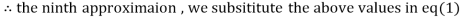
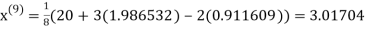
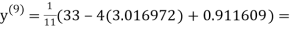 1.985792
1.985792
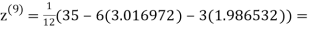 0.911547
0.911547
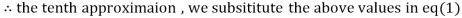
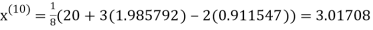
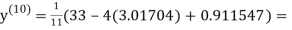 1.98576
1.98576
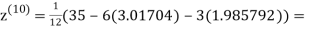 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 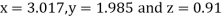
Example2 Solve by Jacobi’s Method, the equations
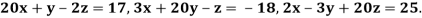
Given equation can be rewrite in the form
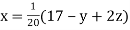 … (i)
… (i)
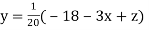 ...(ii)
...(ii)
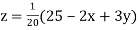 ...(iii)
...(iii)
Let the initial approximation be 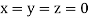
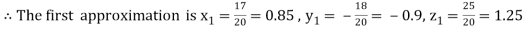
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
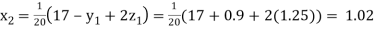
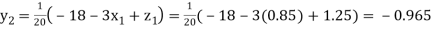
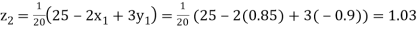
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
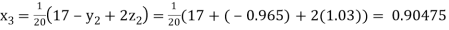
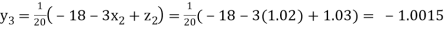
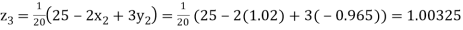
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
 0.90025
0.90025
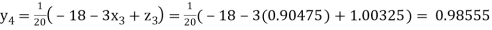
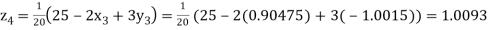
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
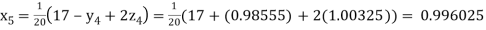
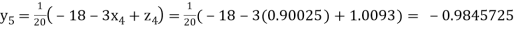
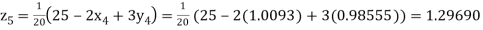
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
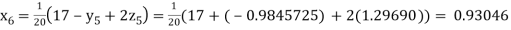

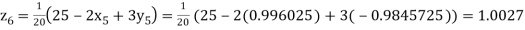
Hence solution approximately is 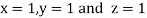
Example3Use Jacobi’s method to solve the system of the equations

Rewrite the given equations
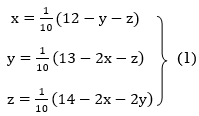
Let the initial approximation be 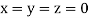
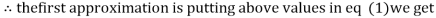
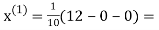 1.2
1.2
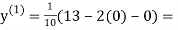 1.3
1.3



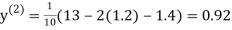
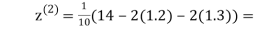 0.9
0.9
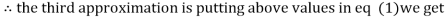
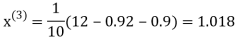
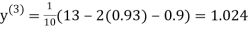
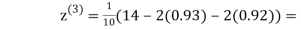 1.03
1.03

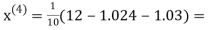 0.9946
0.9946
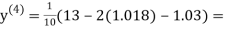 0.9934
0.9934
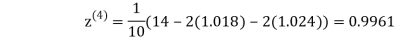
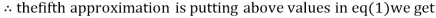
 1.0015
1.0015
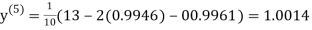
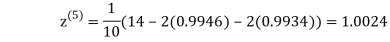
Hence the solution of the above equation correct to two decimal places is
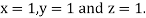
Gauss Seidel method:
This is the modification of the Jacobi’s Iteration. As above in Jacobi’s Iteration, we take first approximation as 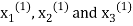 and put in the right-hand side of the first equation of (2) and let the result be
and put in the right-hand side of the first equation of (2) and let the result be 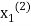 . Now we put
. Now we put 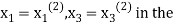 right hand side of second equation of (2) and suppose the result is
right hand side of second equation of (2) and suppose the result is 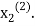 now put
now put 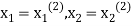 in the RHS of third equation of (2) and suppose the result be
in the RHS of third equation of (2) and suppose the result be 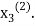 the above method is repeated till the values of all the unknown are found up to desired accuracy.
the above method is repeated till the values of all the unknown are found up to desired accuracy.
Example1 Use Gauss –Seidel Iteration method to solve the system of equations

Since 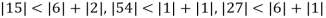
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations

Let the initial approximation be 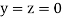
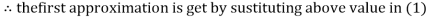
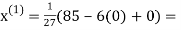 3.14814
3.14814
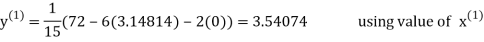

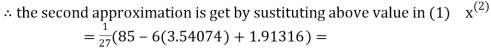 2.43217
2.43217
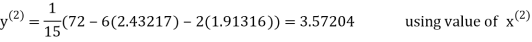
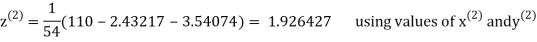
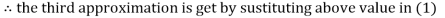
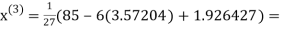 2.42571
2.42571


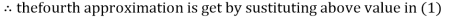
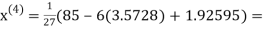 2.4260
2.4260
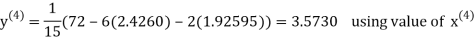
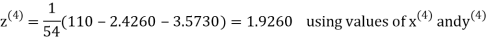
Hence the solution correct to three decimal places is
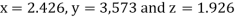
Example2 Solve the following system of equations
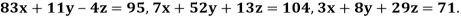 By Gauss-Seidel method.
By Gauss-Seidel method.
Rewrite the given system of equations as
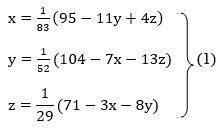
Let the initial approximation be 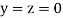

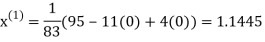
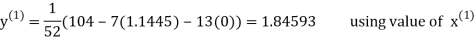
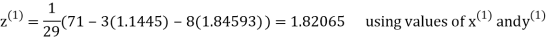
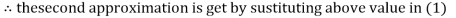
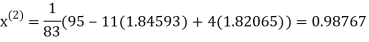
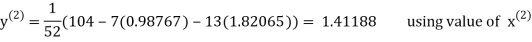
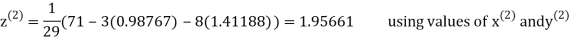
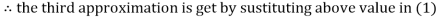
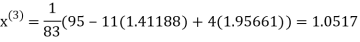
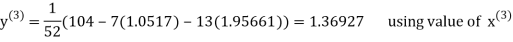

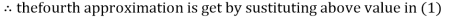

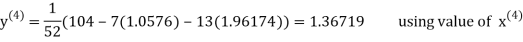
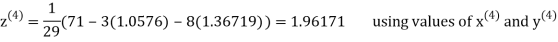
Thus, the required solution is 
Example3 Solve the following equations by Gauss-Seidel Method
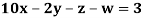
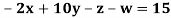
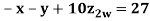
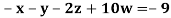
Rewrite the above system of equations
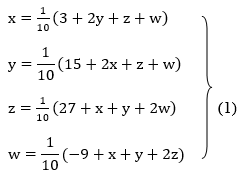
Let the initial approximation be 
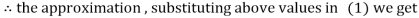
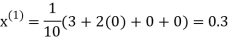
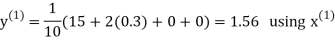
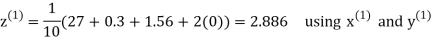
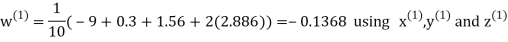

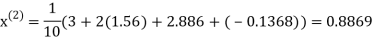
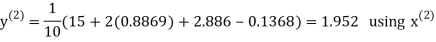
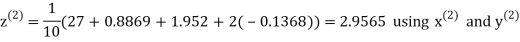
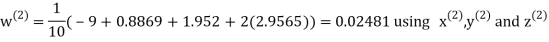

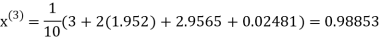
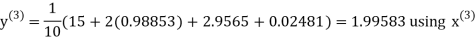
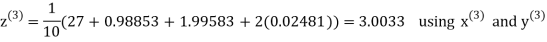
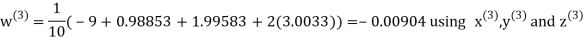

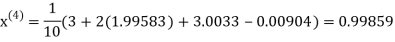
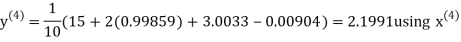
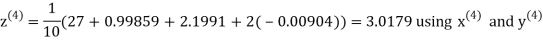
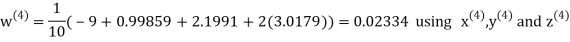

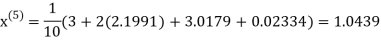
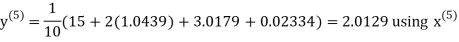
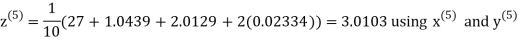
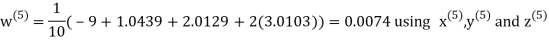
Hence the required solution is 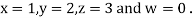
LU decomposition method
The method is based on the fact that every matrix A can be expressed as the product of a lower triangular matrix and an upper triangular matrix.
This method is also known as the Triangularization method
In this method, the coefficient matrix A of the system of equations AX = B is decomposed into the product of a lower triangular matrix L and an upper triangular matrix U so that
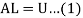
Where
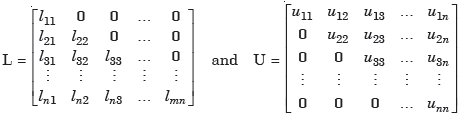
Using the matrix multiplication and comparing corresponding elements in (1), we obtain
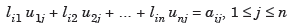
Where
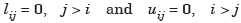
Now
In order to produce a unique solution, it is convenient to choose either 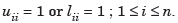
Note-
- When we choose
 = 1, the method is called the Doolittle’s method.
= 1, the method is called the Doolittle’s method. - When we choose
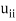 = 1, the method is called the Crout’s method.
= 1, the method is called the Crout’s method.
The given system of equations is
AX = B …… (2)
Using (1)
LUX = B…. (3)
Let UX = Y then equation (3)-
LY = B
y1, y2, y3, ..., yn in (4) are fi by forward substitution and the unknowns x1, x2, x3, ..., xn in UX = Y are obtained by back substitution.
Note- The method fails if any of the diagonal elements 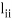 or
or 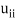 is zero.
is zero.
Example: Solve the equations-

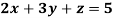
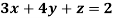
Sol.
Let
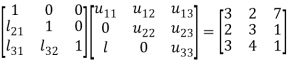
So that-
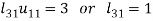
3. 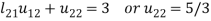
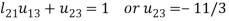
4. 
5. 
So
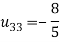
Thus-
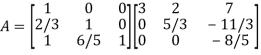
Writing UX = V,
The system of given equations become-

By solving this-
We get-
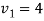
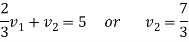
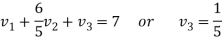
Therefore, the given system becomes-

Which means-

By back substitution, we get the values of x, y and z
Example:
Solve by using Crout’s method, the following system of equations:
x + y + z = 3
2x – y + 3z = 16
3x + y – z = – 3
Sol:
Choosing 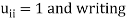
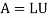
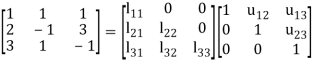
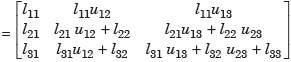
We get by equating
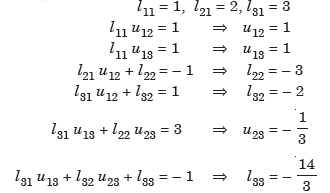
Thus, we get

The given system is
AX = B
LUX = B ... (1)
Let UX = Y so that (1) becomes
LY = B
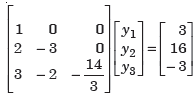
Which gives
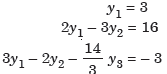
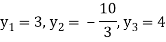
Now
UX = Y
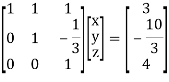
Which gives,
x + y + z = 3
y – z/3 = -10/3
z = 4
By back substitution
X = 1, y = -2 and z = 4
Cholesky’s method
Consider a system of equations
AX = B … (1)
If the coefficient matrix A is symmetric and positive definite then A can be decomposed as
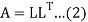
Where L is a lower triangular matrix.
A may also be decomposed as 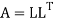 where U is an upper triangular matrix.
where U is an upper triangular matrix.
From (1) and (2),

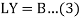
Where
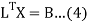
The values  , 1
, 1 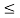 i
i 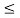 n can be obtained by forward substitution and the solution
n can be obtained by forward substitution and the solution 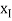 ,,1
,,1 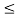 i
i 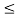 n are obtained by back substitution.
n are obtained by back substitution.
Key takeaways
- When we choose
 = 1, the method is called the Doolittle’s method.
= 1, the method is called the Doolittle’s method. - When we choose
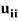 = 1, the method is called the Crout’s method.
= 1, the method is called the Crout’s method. - The method fails if any of the diagonal elements
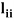 or
or 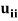 is zero
is zero
Interpolation
Definition:
Interpolation is a technique of estimating the value of a function for any intermediate value of the independent variable while the process of computing the value of the function outside the given range is called extrapolation.
Let  be a function of x.
be a function of x.
The table given below gives corresponding values of y for different values of x.
X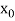
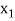
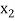 ….
….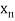
y= f(x)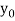
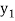
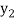 ….
….
The process of finding the values of y corresponding to any value of x which lies between 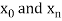 is called interpolation.
is called interpolation.
If the given function is a polynomial, it is polynomial interpolation and given function is known as interpolating polynomial.
Note- The process of computing the value of the function outside the given range is called extrapolation.
Thus, interpolation is the “art of reading between the lines of a table.”
Conditions for Interpolation
1) The function must be a polynomial of independent variable.
2) The function should be either increasing or decreasing function.
3) The value of the function should be increase or decrease uniformly.
Finite Difference
Let 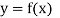 be a function of x. The table given below gives corresponding values of y for different values of x.
be a function of x. The table given below gives corresponding values of y for different values of x.
X
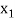
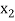 ….
….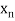
y= f(x)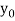
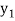
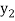 ….
….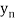
There are three types of differences are useful-
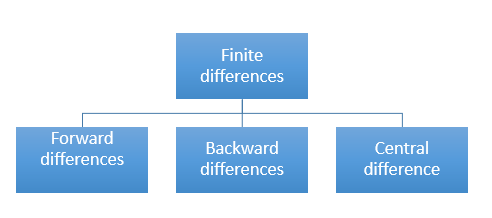
a) Forward Difference:
The 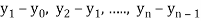 are called differences of y, denoted by
are called differences of y, denoted by 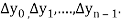
The symbol 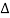 is called the forward difference operator. Consider the forward difference table below:
is called the forward difference operator. Consider the forward difference table below:

Where 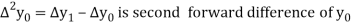
And 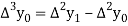 third forward difference so on.
third forward difference so on.
b) Backward Difference:
The difference 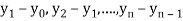 are called first backward difference and is denoted by
are called first backward difference and is denoted by 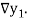 Consider the backward difference table below:
Consider the backward difference table below:

Where 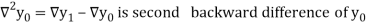
And  third backward differences so on.
third backward differences so on.
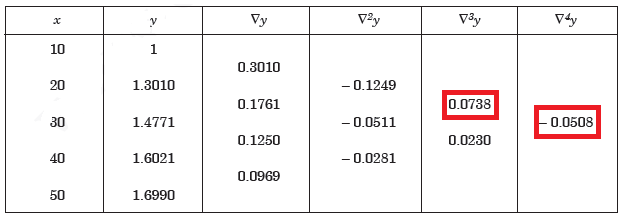
Example: Construct a backward difference table for y = log x, given-
X | 10 | 20 | 30 | 40 | 50 |
y | 1 | 1.3010 | 1.4771 | 1.6021 | 1.6990 |
Sol. The backward difference table will be-
Newton Forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.

Where 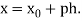
Example1: Using Newton’s forward difference formula, find the sum
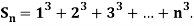
Putting 
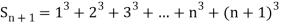
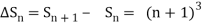
It follows that
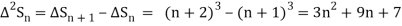
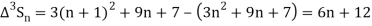
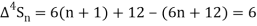
Since 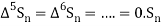 is a fourth-degree polynomial in n.
is a fourth-degree polynomial in n.
Further,
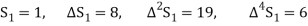
By Newton Forward Difference Method
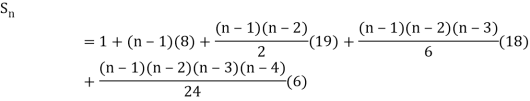

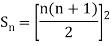
Example2: Given 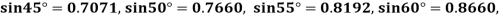 find
find 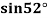 , by using Newton forward interpolation method.
, by using Newton forward interpolation method.
Let  , then
, then
 | 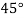 | 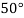 | 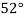 | 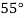 | 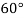 |
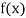 | 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
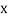 | 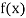 | 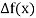 | 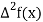 | 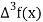 |
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value 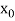 = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.
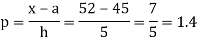
By Formula
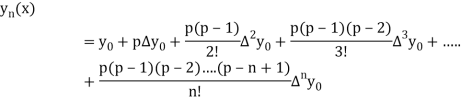

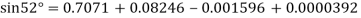
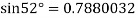
Example3: Find the missing term in the following:
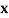 | 0 | 1 | 2 | 3 | 4 |
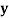 | 1 | 3 | 9 | ? | 81 |
Let 
First, we construct the forward difference table:
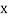 | 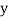 | 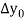 |  | 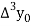 |
0
1
2
3
4 | 1
3
9
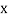
81 |
2
6
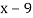
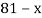 |
4
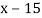
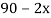 |
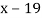
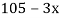 |
Now, 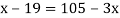
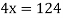
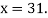
Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
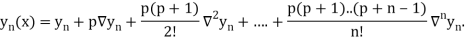
Where 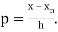
Example1: Find  from the following table:
from the following table:
 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
 | 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
Consider the backward difference method
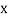 | 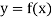 | 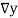 |  | 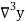 | 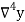 | 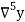 |
0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here 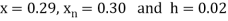
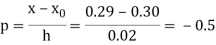
By Newton backward difference formula

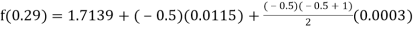
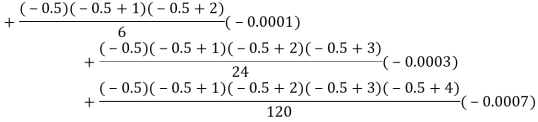
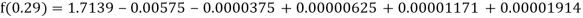
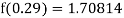
Example2: The following table give the amount of a chemical dissolved in water:
Temp. | 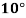 | 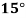 | 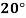 | 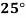 | 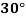 | 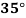 |
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
Compute the amount dissolve at 
Consider the following backward difference table:
Temp. x | Solubility y | 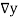 | 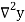 | 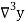 |  |  |
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here 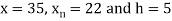
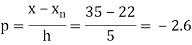
By Newton Backward difference formula

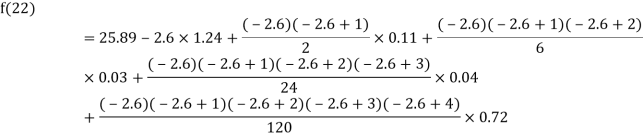


Example3: The following are the marks obtained by 492 candidates in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
Consider the forward difference table given below:
Marks up to x | No. Of candidates y | 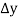 | 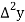 | 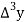 | 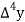 | 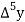 |
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here 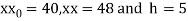
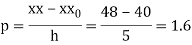
By Newton Forward Difference formula
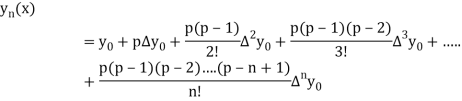
f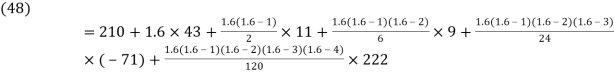
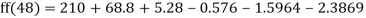
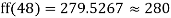
a) No. Of candidate secured more than 48 but not more than 50 marks
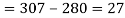
b) No. Of candidate secured less than 48 but not less than 45 marks
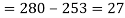
Key takeaways-
- Interpolation is a technique of estimating the value of a function for any intermediate value of the independent variable while the process of computing the value of the function outside the given range is called extrapolation.
- If the given function is a polynomial, it is polynomial interpolation and given function is known as interpolating polynomial.
c) Forward Difference: The 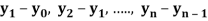 are called differences of y, denoted by
are called differences of y, denoted by 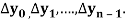
The symbol 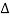 is called the forward difference operator
is called the forward difference operator
3. Backward Difference:
The difference 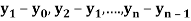 are called first backward difference and is denoted by
are called first backward difference and is denoted by 
- Newton Forward Difference formula:
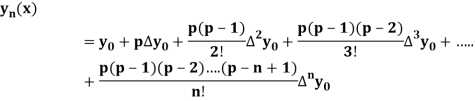
Where 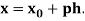
2. Newton Backward Difference Method:
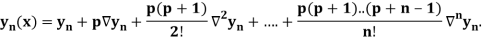
Where 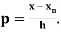
Divided Difference:
In the case of interpolation, when the value of the arguments are not equi-spaced (unequal intervals) we use the class of differences called divided differences.
Definition: The difference which are defined by taking into consideration the change in the value of the argument is known as divided differences.
Let 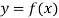 be a function defined as
be a function defined as
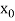 | 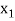 | 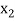 | ……. | 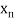 |
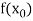 | 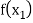 | 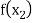 |
………… | 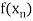 |
Where  are unequal i.e., it is case of unequal interval.
are unequal i.e., it is case of unequal interval.
The first order divided differences are:
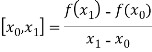

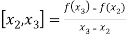 And so on.
And so on.
The second order divided difference is:
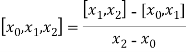
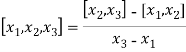
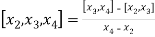 And so on.
And so on.
Similarly, the nth order divided difference is:
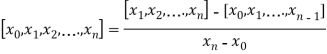
With the help of these we construct the divided difference table:
X | f(x) | 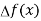 | 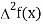 |
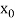

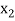 | 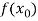

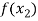 |
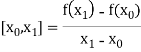
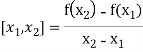 |
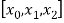  |
Newton’s Divided difference Formula:
Let  be a function defined as
be a function defined as
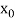 | 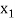 | 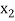 | ……. | 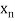 |
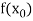 |  | 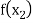 |
………… | 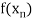 |
Where 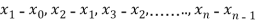 are unequal i.e., it is case of unequal interval.
are unequal i.e., it is case of unequal interval.
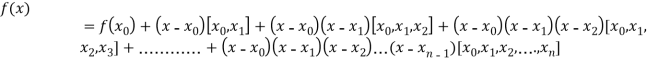 .
.
Example1: By means of Newton’s divided difference formula, find the values of 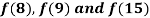 from the following table:
from the following table:
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
We construct the divided difference table is given by:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference | Fourth order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
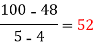
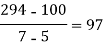

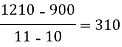
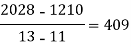 |
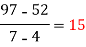

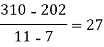
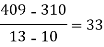 |


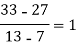 |
0
0 |
By Newton’s Divided difference formula
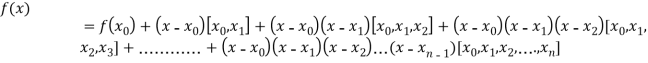 .
.
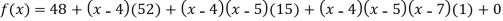
Now, putting 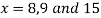 in above we get
in above we get
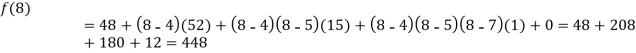 .
.
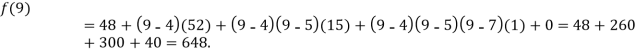
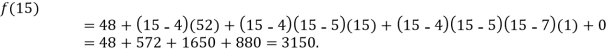
Example2: The following values of the function f(x) for values of x are given:
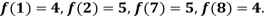
Find the value of 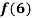 and also the value of x for which f(x) is maximum or minimum.
and also the value of x for which f(x) is maximum or minimum.
We construct the divide difference table:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference |
1
2
7
8 | 4
5
5
4 |
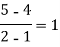
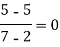
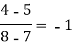
|
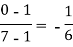
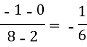
|
0 |
By Newton’s divided difference formula
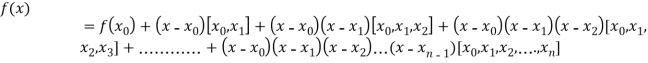 .
.
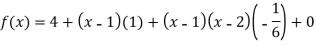
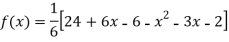

Putting  in above we get
in above we get
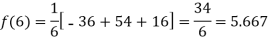
For maximum and minimum of 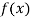 , we have
, we have
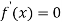

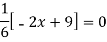
Or 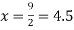
Example3: Find a polynomial satisfied by 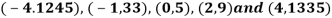 , by the use of Newton’s interpolation formula with divided difference.
, by the use of Newton’s interpolation formula with divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
We will construct the divided difference table:
x | F(x) | First order divided difference | Second order divided difference | Third order divided difference | Fourth order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
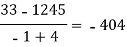
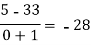
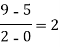
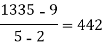
|
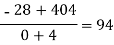
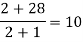
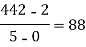 |
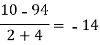
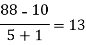 |
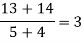 |
By Newton’s divided difference formula
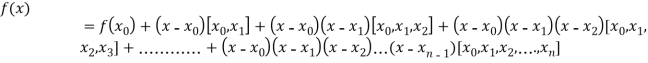 .
.
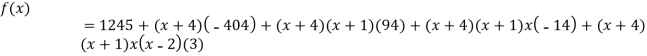
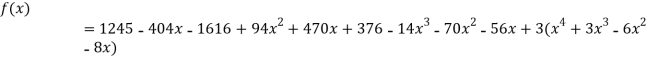
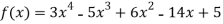
This is the required polynomial.
Key takeaways
- When the value of the arguments are not equi-spaced (unequal intervals) we use the class of differences called divided differences.
- Newton’s Divided difference Formula
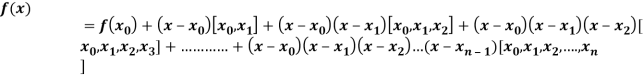 .
.
Lagrange’s interpolation of polynomial:
Let 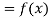 , be defined function we get
, be defined function we get
X | 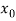 | 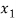 | 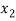 | ….. | 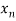 |
f(x) | 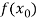 | 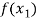 | 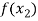 | …… | 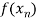 |
Where the interval is not necessarily equal. We assume f(x) is a polynomial od degree n. Then Lagrange’s interpolation formula is given by
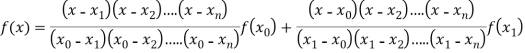

Example1: Deduce Lagrange’s formula for interpolation. The observed values of a function are respectively 168,120,72 and 63 at the four position3,7,9 and 10 of the independent variables. What is the best estimate you can for the value of the function at the position6 of the independent variable?
We construct the table for the given data:
X | 3 | 6 | 7 | 9 | 10 |
Y=f(x) | 168 | ? | 120 | 72 | 63 |
We need to calculate for x = 6, we need f (6) =?
Here 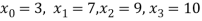
We get 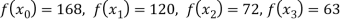
 By Lagrange’s interpolation formula, we have
By Lagrange’s interpolation formula, we have
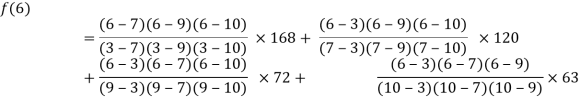
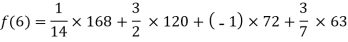

Hence the estimated value for x=6 is 147.
Example2: By means of Lagrange’s formula, prove that
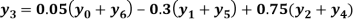
We construct the table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Y=f(x) |  | 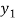 |  | 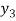 |  | 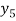 | 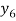 |
Here x = 3, f(x)=?
 By Lagrange’s formula for interpolation
By Lagrange’s formula for interpolation
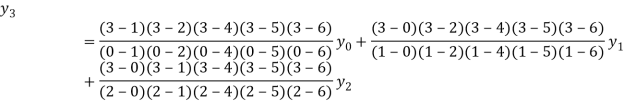
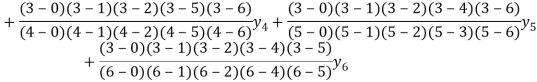

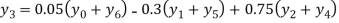
Hence proved.
Example3: find the polynomial of fifth degree from the following data
X | 0 | 1 | 3 | 5 | 6 | 9 |
Y=f(x) | -18 | 0 | 0 | -248 | 0 | 13104 |
Here 
We get 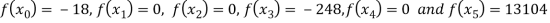
 By Lagrange’s interpolation formula
By Lagrange’s interpolation formula
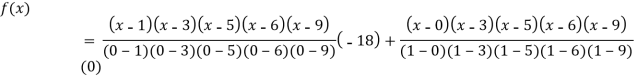
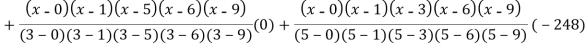
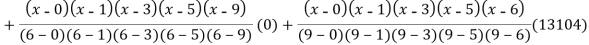
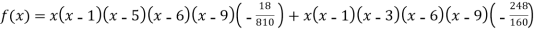
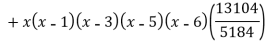
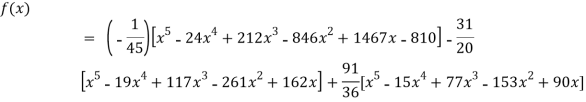
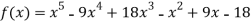
Key takeaways
Then Lagrange’s interpolation formula is-
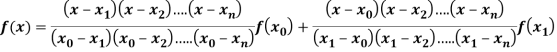
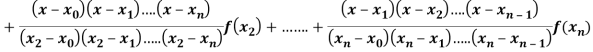
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- Higher engineering mathematics, BV Ramana.
- Computer based numerical & statistical techniques, M goyal