Unit - 2
Fluid Kinematics
- Fluid kinematics is the branch of fluid mechanics which deals with the study of velocity and acceleration of the particles of fluid in motion and their distribution in space without consideration of any forces or energy involved.
- Motion of fluid can be described fully by an expression describing the location of the fluid particle in space at different times thus enabling determination of the magnitude and direction of velocity and acceleration in the flow field at any instant of time.
- Steady and unsteady flow
- Uniform and non-uniform flow
- Laminar and turbulent flow
- Compressible and incompressible flow
- Rotational and irrotational flow
- One, two and three-dimensional flow
- Subcritical and supercritical flow
- Sonic, subsonic and supersonic flow
1. Steady and Unsteady Flow:
Steady Flow
- The flow in which fluid characteristics like velocity, pressure, density etc. at a point do not change with time is called as steady flow.
- E.g., flow of water with constant discharge through a pipeline is as steady flow.
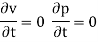
Unsteady Flow
- The flow in which fluid characteristics like velocity, pressure, density etc. at a point change with time is called as unsteady flow.
- E.g., flow of water with varying discharge through a pipe is as unsteady flow.
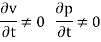
2. Uniform and Non-uniform Flow:
Uniform Flow
- The flow in which velocity at a given time does not change with respect to space (length of direction of flow) is called as uniform flow.
- E.g., flow through a long straight pipe of uniform diameter is consider as uniform flow.
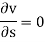
Non-Uniform Flow
- The flow in which velocity at a given time changes with respect to space (length of direction of flow) is called as non- uniform flow.
- E.g., flow through a long pipe with varying cross section is consider as non-uniform flow.

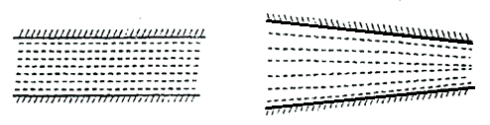
Fig 1: Uniform and Non-uniform velocity
3. Laminar and Turbulent Flow:
Laminar Flow
- The flow in which the adjacent layer does not cross to each other and move along the well define path is called as laminar flow.
- E.g., flow of blood in small veins, flow of oil in bearings, flow in porous media, flow of highly.
Turbulent Flow
- The flow in which the adjacent layer cross to each other and do not move along the well define path is called as turbulent flow.
- E.g., flow through a river or canal, smoke from chimney, smoke from a cigarette.
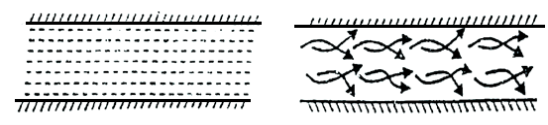
Fig 2: Laminar and Turbulent flow
If Reynold's number is less than 2000, then the flow is laminar.
If Reynold's number is more than 4000, then the flow is turbulent.
If Reynold's number is between 2000 to 4000, then the flow is transit.
Reynold's number
- Reynold's number is defined as the ratio of the inertia force of the fluid to the viscous force.
- Reynold's number=Inertia force/Viscous force
4. Compressible and Incompressible flow:
Compressible Flow
- The flow in which the density does not constant for the fluid flow is called as compressible flow.
- E.g., problems involving flight of rockets, aircrafts, flow of air in problems concerned with turbo machines, compressor blades, flow of gases through openings like nozzles.

Incompressible Flow
- The flow in which the density is constant for the fluid flow is called as incompressible flow.
- E.g., problems involving liquids i.e., hydraulics problems, flow of gases in machines like fans and blowers.
 = constant
= constant
5. Rotational and Irrotational Flow

Fig 3: Rotational and Irrotational motion
Rotational Flow
- The flow in which the fluid particle while flowing along stream lines, also rotate about their own axis is called as rotational flow.
- E.g., motion of liquid in a rotating cylinder (forced vortex) as rotational flow.
Irrotational Flow
- The flow in which the fluid particle while flowing along streamlines, do not rotate about their own axis is called as irrotational flow.
- E.g., flow of liquid in an emptying wash-basin (free vortex) as an irrotational flow.
6. One, Two and Three Dimensional Flow
One-dimensional flow
- The flow in which the velocity is the function of time and one space co-ordinate (x) is called as One-dimensional flow.
- E.g., flow through the pipe is consider as a one-dimensional flow.
u = f(x), v=0, w=0
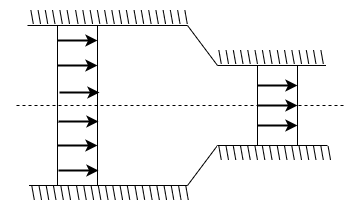
Fig 4: One-dimensional flow
Two-Dimensional Flow
- The flow in which the velocity is the function of time and two space co-ordinate (x, y) is called as two-dimensional flow.
- E.g., viscous flow between parallel plates of large extent, flow at the middle part of airplane wing, flow over a long spillway, flow below long weirs are considered as a two-dimensional flow.
u = f1(x, y) v= f2 (x, y) w=0

Fig 5: Two-dimensional flow
Three-Dimensional Flow
- The flow in which the velocity is the function of time and three space co-ordinate (x, y, z) is called as three-dimensional flow.
- E.g., flow is converging or diverging pipes or open channels are as three-dimensional flow. Flow in a river, flow at an inlet of a nozzle etc. are the example of three-dimensional flow.
u = f₁ (x, y, z), v=f₂ (x, y, z), w=f3 (x, y, z) =0
Where u, v, w are the velocities in x, y, z direction.
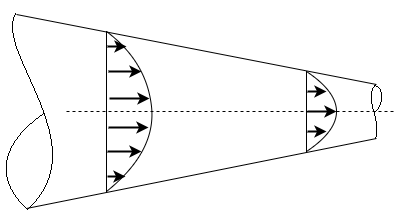
Fig 6: Three-dimensional flow
7. Critical, Subcritical and Super Critical
Critical flow
- When the Froude number is equal to unity and mean velocity of flow V=
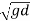 the flow is called as critical flow.
the flow is called as critical flow.
Fr=1
Subcritical flow
- When Froude number is less than one or V=
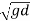 , the flow is said to be subcritical flow or tranquil or streaming flow.
, the flow is said to be subcritical flow or tranquil or streaming flow.
Fr < 1
Supercritical flow
- When the Froude number is greater than one of V=
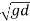 , the flow is said to be super critical flow or rapid flow or shooting flow.
, the flow is said to be super critical flow or rapid flow or shooting flow.
Fr > 1
Where D= hydraulic depth of channel
8. Sonic, Subsonic and Supersonic Flow
- Sonic flow: The flow for which Mach number is equal to unity.
- Subsonic flow: For this Mach number 'M' is in between range 0.4 to 1.0.
- Supersonic flow: Mach number for this flow is always greater than unity but less than six.
Key Takeaways:
- Steady and unsteady flow
- Uniform and non-uniform flow
- Laminar and turbulent flow
- Compressible and incompressible flow
- Rotational and irrotational flow
- One, two and three-dimensional flow
- Subcritical and supercritical flow
- Sonic, subsonic and supersonic flow
- The ratio of inertia force to the viscous force is called as Reynold's number. It is denoted by Re.
=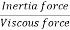
=
=
=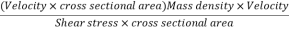
=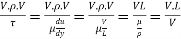 ∵
∵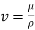
Application:
- Motion of completely submerged bodies like submarine, aeroplanes and automatic with low velocity, Incompressible flow through pipes, flow through low-speed turbo machine in which viscous forces are predominant.
Key Takeaways:
The ratio of inertia force to the viscous force is called as Reynold's number. It is denoted by Re.
= (Inertia force)/ (Viscous force)
Types of Acceleration of Fluid Component are as follows:
- Tangential and Normal Acceleration
- Material Acceleration or Substantial Acceleration
- Local Acceleration or Temporal Acceleration
- Convective Acceleration
Tangential and Normal Acceleration
- Let’s and n represent the tangential and normal direction respectively at any point on the streamlines as shown in Fig.
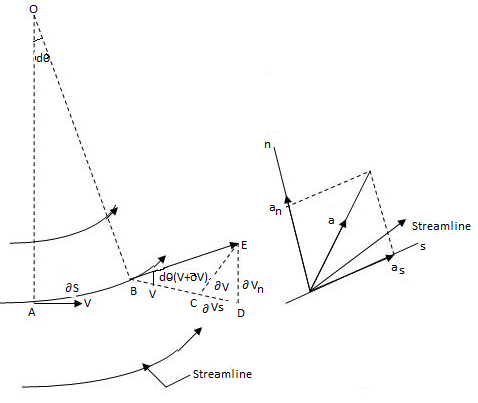
Fig: 7
- Let as = Tangential acceleration in s direction
- an = Normal acceleration in n direction
- The tangential component of the acceleration is due to the change in the magnitude of velocity along the streamline is called as tangential acceleration.
- It is denoted by as.
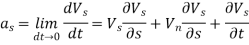
- The normal component of the acceleration is due to the change in the direction of velocity vector is called as normal acceleration. It is denoted by an.
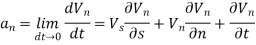
- For any streamline,
Vn=0
∴
∴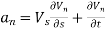
- For steady flow, velocity does not change with respect to time. i.e.,
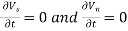
∴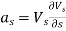 ,
, 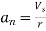
Where r is the radius of curvature of the streamline.
Material Acceleration or Substantial Acceleration
- The rate of increase in velocity due to both time and position of fluid particle is called as material acceleration. It is the total acceleration of fluid particle.
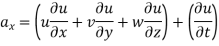
Local Acceleration or Temporal Acceleration
- The rate of increase of velocity with respect to time at a given point in a flow field is called as local acceleration. For steady flow, "local acceleration is zero,
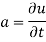
Convective Acceleration
- The rate of increase of velocity with respect to changes in the position of fluid particle in a flow field is called as convective acceleration. For steady flow, convective acceleration is not zero. In uniform flow, the convective acceleration is zero.

Key Takeaways:
Types of Acceleration of Fluid Component are as follows:
- Tangential and Normal Acceleration
- Material Acceleration or Substantial Acceleration
- Local Acceleration or Temporal Acceleration
- Convective Acceleration
- Continuity equation is based on the principle of conservation of mass. It states that mass can neither be created nor destroyed. The mass accumulated equals the rate of change of mass between the two sections.
- Consider a stream tube as shown in Fig., Fluid flow enters in the tube al section 1-1 and fluid flow exist from the tube at section 2-2. Two sections at a distance ds apart in a stream tube.
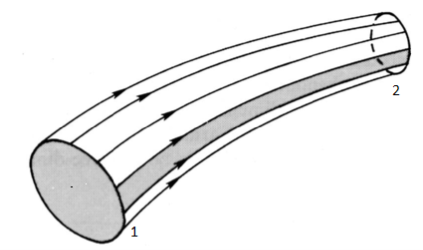
Fig: 8
- Rate of increase of mass within the body Mass flow rate enters-Mass flow rate exists
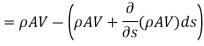
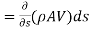 …(1)
…(1)
- Now rate of increase of mass between the two sections
 mass=
mass=  volume
volume
=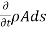 …(2)
…(2)
- By law of conservation of mass, Equating Equations 1 and 2
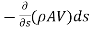 =
=
∴ 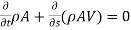
- This is the general continuity equation for one-dimensional flow based on stream tube concept.
- For steady flow
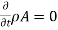 ∴
∴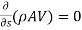
- For incompressible flow p is constant,
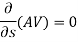
Integrating w.r.t ds,
∴ AV = constant.
∴ A₁V₁= A2V2
Key Takeaways:
Continuity equation is based on the principle of conservation of mass. It states that mass can neither be created nor destroyed. The mass accumulated equals the rate of change of mass between the two sections.
- Continuity equation is based on the principle of conservation of mass.
- Consider a fluid element of lengths dx, dy, dz in the direction of x, y, z.
- Let u, v, w are the inlet velocity components in x, y, z direction respectively.
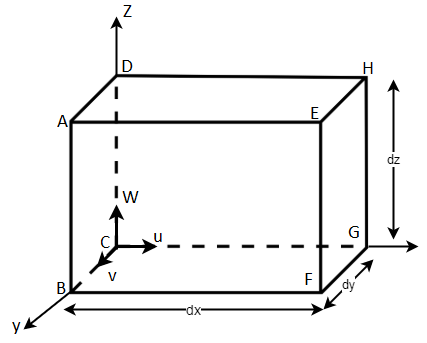
Fig: 9
- Let
 is mass density of fluid element at particular instant.
is mass density of fluid element at particular instant. - Mass of fluid entering the face ABCD (In flow)
= Mass density x Velocity x-direction X Area of ABCD
= 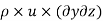
Then mass of fluid leaving the face EFGH (out flow)
=
Rate of increases in mass x-direction = Outflow - Inflow
= 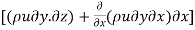 –(
–( 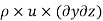 )
)
Rate of increases in mass x direction
=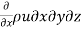
Similarly, Rate of increases in mass y-direction
= 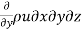
Rate of increases in mass z-direction
= 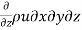
Total rate of increases in mass
= 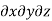
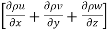
By law of conservation of mass, there is no accumulation of mass, and hence the above quantity must be zero.
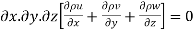
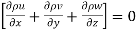 ...for compressible fluid
...for compressible fluid
If fluid is incompressible, then 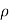 is constant
is constant
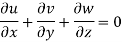
This is the continuity equation for three-dimensional flow.
Now, for two-dimensional flow, the velocity component w=0
Hence continuity equation is,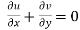
Key Takeaways:
Continuity equation is based on the principle of conservation of mass.
Rotational flow:
- Flow is said to be rotation, when every fluid element rotates at its axis which is perpendicular to the plane of motion.
- Consider a rectangular fluid element ABCD at a certain time in a two-dimensional x - y plane.
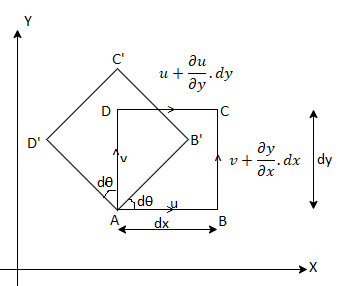
Fig: 10
The velocity components x-direction at A and D are, u and 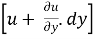 respectively.
respectively.
The velocity component in y-direction at B and D are, v and 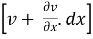 respectively.
respectively.
- Since these velocities are different, there will be angular velocity developed for linear element AD and AB respectively.
- In time interval dt, the elements AB and AD would move relative to point A, the fluid element takes position AB'C'D'.
- Consider anti-clockwise rotation as positive, the angular velocity of element AB at z-axis is,
We know, L=r and
and 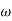 =
=  ,
,
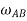 =
= 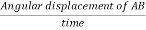
= 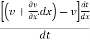
= 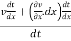 =
= 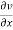
Perpendicularly angular displacement at AD about Z-axis,
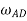 = -
= - (Moment is positive,
(Moment is positive, 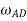 =-ve)
=-ve)
The average of angular velocities of two mutually perpendicular elements gives the rotation about Z-axis.
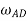 =
= 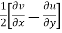
For these dimensional fluid, three-rotational components are given by,
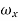 =
= 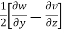
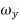 =
= 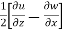
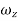 =
= 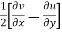
Rotational vector,  =
= 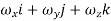 =
=  Curl.v
Curl.v
Irrotational Flow:
When the rotational component 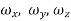 of every point of flowing fluid are equal to zero, then flow is said to be irrotational flow.
of every point of flowing fluid are equal to zero, then flow is said to be irrotational flow.
Condition for irrotational flow,
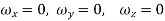
OR curl V=V  v = 0
v = 0
Substituting u =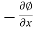 , and v =
, and v =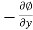 in Equations (5.8.1), (5.8.2) and (5.8.3),
in Equations (5.8.1), (5.8.2) and (5.8.3),
Rotational components,
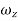 =
= 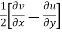
= 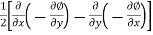
=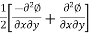
Perpendicularly, 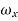 =
=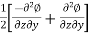 ,
,
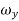 =
= ,
,
If is continuous function,
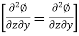 ,
,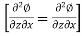 ,
,

When rotational component is zero, the flow is irrotational.
- In rotational motion, circulation is a very useful concept. Circulation around a closed curve C is defined as the line integrate of the tangential component of the velocity taken round a closed curve C taken positive in anticlockwise direction. The flow along a closed curve called as circulation.
- E.g., flow in eddies and vortices

Fig 11: Circulation concept
Key Takeaways:
In rotational motion, circulation is a very useful concept. Circulation around a closed curve C is defined as the line integrate of the tangential component of the velocity taken round a closed curve C taken positive in anticlockwise direction. The flow along a closed curve called as circulation.
Potential function:
- It is defined as a scalar function of space and time such that its negative derivative with respect to any direction gives the fluid velocity in that direction. It is denoted by
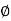 (Phi).
(Phi). - For steady flow velocity potential
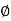 = f (x, y, z).
= f (x, y, z).
u =-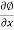 , v=
, v=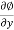 , w=
, w=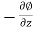
- Negative sign indicate that flow take place in the direction in which '
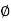 ' decreases
' decreases - Continuity equation for steady flow,
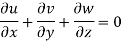
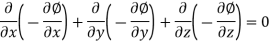
∴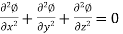 is a Laplace equation,
is a Laplace equation,
- For two-dimensional,
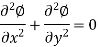
Properties of Potential Function
- If velocity potential (
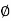 ) exist, the flow is irrotational.
) exist, the flow is irrotational. - If the velocity potential (
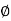 ) satisfies the Laplace equation, it represents the possible steady incompressible irrotational flow.
) satisfies the Laplace equation, it represents the possible steady incompressible irrotational flow.
Stream Function:
- It is defined as the scalar function of space and time, such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction. It is denoted by
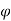 (Psi) and defined only two-dimensional flow.
(Psi) and defined only two-dimensional flow. - For steady flow,
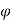 =f (x, y) such that,
=f (x, y) such that,

Properties of Stream function:
- If stream function exists, it is a possible case of fluid flow which may be rotational or irrotational.
- If stream function satisfies the laples equation, it is a possible case of an irrotational flow.
Key Takeaways:
- It is defined as a scalar function of space and time such that its negative derivative with respect to any direction gives the fluid velocity in that direction. It is denoted by
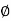 (Phi).
(Phi). - It is defined as the scalar function of space and time, such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction. It is denoted by
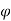 (Psi) and defined only two-dimensional flow.
(Psi) and defined only two-dimensional flow.
- A grid obtained by drawing a series of streamlines y and equipotential lines is known as a flow net.
- Flow net provides a simple graphical technique for studying two-dimensional irrotational flows, when the mathematical calculation is difficult and cumbersome.
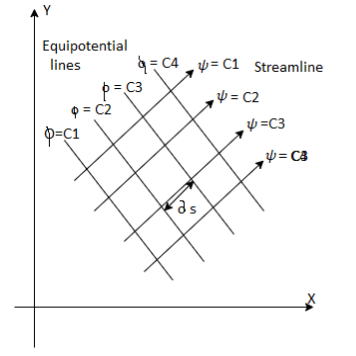
Fig 12: Flow net
- The streamlines y and equipotential lines are mutually perpendicular to each other.
- The stream lines are so spaced that rate of flow Q is same between each successive pair of lines.
- The stream lines in flow net show the direction of flow and the equipotential lines join the points the equal velocity potential
 .
.
Condition for Drawing Flow Net:
- The flow net should be steady so that the stream line patterns will remain constant.
- The flow should be irrotational which has negligible viscosity.
- Flow net should not be governed by the gravity force to maintain the fixed pattern of flow net.
Uses of Flow Net:
- To determine the amount of seepage and upward lift pressure below hydraulic structure.
- Once the flow net is constructed, the same one applies to flows at different discharges.
- If the velocity of any reference point is known, the flow net gives velocity at any point by using continuity equation.
- A flow net analysis assists in the design of an efficient boundary shapes. It helps in avoiding the separation and the points of stagnation in the design of boundary shapes.
Limitation of Flow Net:
- The flow net analysis cannot be applied in the region closed to the boundary where the effects of viscosity are predominant.
- The flow net is not applied to a sharply diverging flow, as the actual flow pattern is not represented by the flow net.
- Flow net are unable to show the formation of wakes due to the separation and eddies.
Key Takeaways:
A grid obtained by drawing a series of streamlines y and equipotential lines is known as a flow net.
Numericals:
Q.1 The velocity components for a two-dimensional incompressible flow is given by
1) u = 4 xy + y². v = 6 xy + 3x
2) 
Check whether the flow satisfies continuity?
Soln.:
(i) u = 4 xy + y², v = 6 xy + 3x
Differentiating
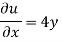

For two-dimensional flow continuous equation is
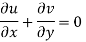
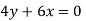
Velocity components does not satisfy the continuity equation
Ii) 
Differentiating

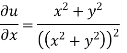
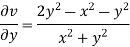
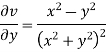
For two-dimensional flow continuous equation is
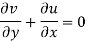
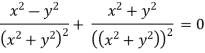
Satisfy the continuous equation.
Q.2 The velocity components for a three-dimensional incompressible flow is given by: 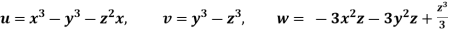
Check whether the flow satisfies continuity?
Soln.:
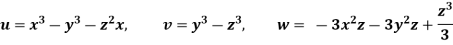
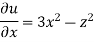
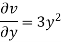
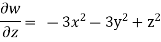
Foe three-dimensional equation continuous equation is
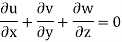
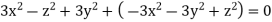
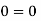
The flow is satisfied
Q.3 The velocity field is given by  check whether the flow satisfies continuity?
check whether the flow satisfies continuity?
Soln.:
Velocity field

Velocity component
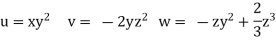
For three-dimensional flow
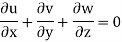
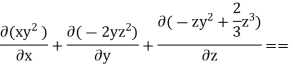
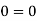
Steady incompressible fluid flow is possible.
References:
1. Fluid mechanics and machinery R Berndtsson and P.N. Chadramouli
2. Hydraulic and fluid mechanics, PM Modi and SM Seth
3. Theory and applications of fluid mechanics, K Subramanya, Tata McGraw Hill
4. Fluid mechanics with engineering applications, RL Daughterty, JB Franzini