Unit - 1
Introduction
- The flight of birds in the air and the motion of the fish in the water are governed by the law of fluid mechanics.
- The cricket ball bowling depends upon circulation principle to provide the ball with desired spin and flight.
- The circulation of blood in veins and arteries follows the law of fluid resistance.
- The design of aeroplanes and ships are based on the theory of aerodynamics and buoyancy.
- The oil and gas pipelines, the water supply systems are designed on the principles of fluid mechanics.
Key Takeaways:
The design of aeroplanes and ships are based on the theory of aerodynamics and buoyancy. The oil and gas pipelines, the water supply systems are designed on the principles of fluid mechanics.
- The density of a fluid is defined as the mass per unit volume.
- It is denoted by 'p' (rho). S.I. Unit is kg/m³.
- Mass density of water is 1000kg/m³.
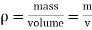
- Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
- It is denoted by S or RD.
- Specific gravity
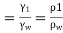
- For liquid, water and for gases, hydrogen or air is consider as a standard fluid.
- Specific gravity of water at a standard temperature 4°C is 1 and that of mercury is 13.6.
Key Takeaways:
Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
- The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
- It is denoted by 'w' or '
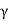' (gamma). It has S.I. Unit is N/m3. - Specific weight of water is 9810 N/m³ (9.81 kN/m³).
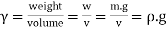
- The specific weight depends on gravitational acceleration and the mass density. Since gravitational attraction varies from place to place, the specific weight will also vary.
Key Takeaways:
The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
- Specific volume of a liquid is the volume of the fluid per unit weight. It is the reciprocal of specific weight.
- It is denoted by 'V'. S.I. Unit is m³/N.
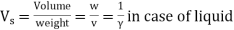
- For the gas flow, specific volume is defined as the volume of the fluid per unit mass. In this case it is a reciprocal of mass density. S.I. Unit is m3/kg.
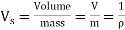in case of gas
Key Takeaways:
Specific volume of a liquid is the volume of the fluid per unit weight. It is the reciprocal of specific weight.
- The surface tension of a liquid is the property by which a fluid is enables to resist tensile stress.
- It is due to the cohesion between the molecules at the surface of a liquid. It is the force required to maintained unit length of the film in equilibrium. It is denoted by '
' (sigma). S.I. Unit = N/m. - All liquid molecules have tendency to attract each other.
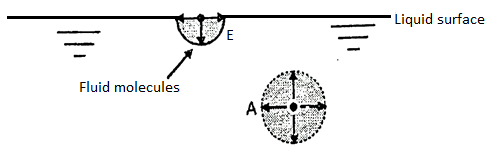
Fig: 1
- A liquid molecule on the interior of the liquid body has other molecules on all side of its, so that the forces of attraction are in equilibrium and the molecule is equally attracted on all sides, as a molecule at point A as shown in Fig.
- A liquid molecule at the free surface at point B, does not have liquid molecule above it to pull them outward, so that the free surface molecule tries to move towards the center by downward force.
- This force on the liquid surface is normal to the liquid surface. A film or layer is occurring on the liquid surface which is in tension and resist small loads if placed gently over it.
- It occurs at the interface of a liquid and a gas or at the interface of two liquids and is essentially due to intermolecular forces of cohesion.
- As the temperature increases, the surface tension is decreases.
e.g.
- A small needle placed gently upon the water surface will not sink but will be supported by the tension at the water surface.
- The effect of surface tension is to reduce the surface of a free body of liquid to a minimum. That is why falling drops of rain become spherical shape.
- Surface tension force can be reduced by the addition of detergents. Surface tension value of liquids when it is cannot with air
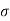= 0.073 N/m for air-water interface
= 0.480 N/m for air-mercury interface
- Surface tension leads to the phenomena of capillary waves on a liquid surface and capillary rise or depression.
Pressure Intensity Inside a Droplet:
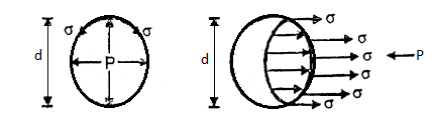
Fig: 2
- Consider a spherical droplet of diameter 'd'. Let the excess pressure developed inside the droplet 'P' and '
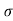' is the surface tension in the surface of droplet as shown in Fig. - For static equilibrium condition
- Surface tension force = Force due to excess pressure
- Surface tension x Circumference = Excess pressure x Normal area
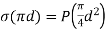∴P=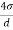
- Thus, pressure intensity inside a droplet varies inversely with the diameter. Pressure intensity decreases with an increase in the size of the droplet.
Pressure Intensity Inside a Soap Bubble:
- Soap bubble has two surfaces in contact with air, inside and outside.
- Consider a soap bubble of external diameter d and thickness of bubble=
d as shown in Fig.
= Surface tension on inner surface
= Surface tension on outer surface
- For static equilibrium,
Force due to excess pressure = Force due to surface tension
Excess pressure x Normal area= Surface tension x Circumference
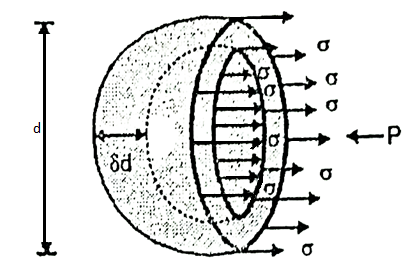
Fig: 3
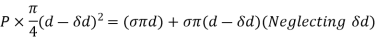
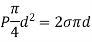
∴P=
- Thus, excess pressure inside the soap bubble is twice as that of droplet.
Pressure Intensity Inside a Liquid Jet:
Fig: 4
- Consider a liquid jet as a cylinder of diameter ‘d’ and length ‘l’ as shown in fig.
- Force due to excess pressure = Force due to surface tension
- Excess pressure x Normal area = Surface tension x Circumference
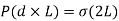
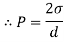
Application of Surface Tension:
- Formation of droplets.
- Ability of needle to float on water.
- Falling drop become spherical shape.
Key Takeaways:
The surface tension of a liquid is the property by which a fluid is enables to resist tensile stress.
- When a small diameter tube less than 6 mm is inserted vertically inside a pool of liquid, the liquid level in the tube either rise or falls relatively to the liquid level in the pool.
- This phenomenon of rise or fall of liquid level in the capillary tube is called as capillarity. Capillary is due to cohesion and adhesion.
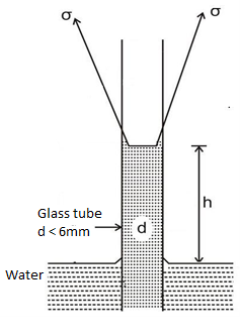
Fig 5: Capillary rise
- If the adhesion force between molecules of liquid and tube is more than cohesion between liquid molecules (e.g., water), the liquid will wet the glass surface and the liquid level will rise.
- The liquid level will become concave upward as shown in Fig.
- In such case angle between surface tension with the vertical (
) is less than 90°. - If cohesive force between molecules of liquid and tube is more than cohesion between liquid molecules (If cohesive force predominate)
- E.g., mercury, the liquid does not wet the surface, liquid level will fall as shown in Fig.
- The liquid became convex upwards in such case angle between surface tension with the vertical (
) is greater than 90° - E.g., suction of kerosene in lamp, rise of water in soil are example of capillarity
Fig 6: capillary fall
Expression for Capillary Rise:
- Let h be the capillary rise or fall in a tube of diameter 'd' centre surface tension force in upward direction.
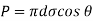
Weight of liquid column
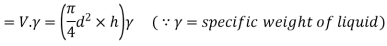
- Under equilibrium, the weight of liquid column will be balanced by surface tension force '
'.
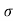Weight of liquid = Surface tension force
∴
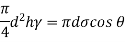
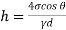
- For pure water in contact with clean glass and air,
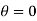
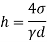
- For mercury and glass,
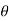= 140°
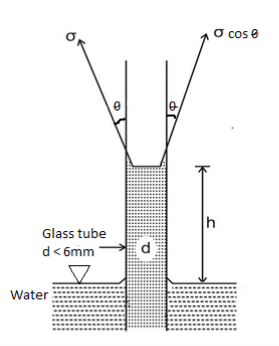
Fig 7: Capillary rise
- Capillary rise Capillary rise in a gap between two closed spaced parallel plate
Where 't' is the gap between the plates.
Application of Capillarity:
- Capillarity action is responsible for moving ground water from wet areas of the soil to dry areas.
- Suction of kerosene in lamp.
Key Takeaways:
When a small diameter tube less than 6 mm is inserted vertically inside a pool of liquid, the liquid level in the tube either rise or falls relatively to the liquid level in the pool. This phenomenon of rise or fall of liquid level in the capillary tube is called as capillarity. Capillary is due to cohesion and adhesion.
- The property by virtue of which, a fluid offers resistance to deformation under the action of a shear force is called as viscosity or dynamic viscosity.
- Consider the behaviour of two layers of fluid moving one over other at a distance 'dy' apart and having velocities (u + du) and u respectively as shown in Fig.
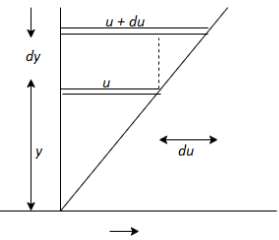
Fig: 8
- As the upper layer moves with higher velocity relative to the lower one, the upper layer will also try to move the lower layer with the same velocity. But lower layer, which move with smaller velocity, will oppose the motion of upper layer.
- Thus, the relative velocity (du) between two adjacent layers together with viscosity causes shear stress acting between the fluid layers.
- It means that upper layer which is moving relative faster causes a shear stress on the lower layer in the direction of flow whereas the lower layer causes a shear stress in opposite direction to the upper layer.
- The tangential stress between two adjoining layers is proportional to velocity gradient (the rate at which velocity changes with the distance across the flow) in a direction perpendicular to the layers. This is known as law of viscosity. It is denoted by
(Tau).
Where,
μ = Coefficient of dynamic viscosity
Du/dy = Velocity gradient or rate of shear strain
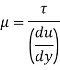
- Thus viscosity is also defined, as the shear stress is required to produce unit rate of shear strain.
S.I. Unit of viscosity:
- The unit of viscosity in CGS is called as poise, which is equal to dyne sec/cm2.
- The viscosity of water at 20°C is 0.01 poise or 1 centi poise.
Key Takeaways:
The property by virtue of which, a fluid offers resistance to deformation under the action of a shear force is called as viscosity or dynamic viscosity.
Compressibility:
- It is the measure of elasticity in fluid.
- Fluids are compressed under pressure due to change in their mass density.
- More mass can be accommodated in the unit volume and when the pressure is removed the fluids regain to its original volume.
- As the pressure is increased, the volume is decreased. Refer Fig.
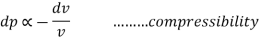
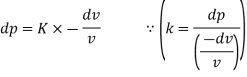
Where K is the constant of proportionality is known as bulk modulus.
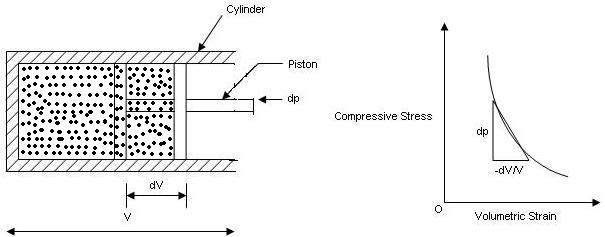
Fig: 9
- If K is more, dv/v is less indicating less volume change i.e., less compressibility. That is why compressibility expressed as inverse of bulk modulus.
- Higher the bulk modulus less is the compressibility of fluid.
- Liquids are generally considered to be incompressible. For instance, a pressure of 113078 kPa will cause a given volume of water to decrease by only 5% from its volume at atmospheric pressure.
- Gases on the other hand, are very compressible. The volume of a gas can be readily changed by exerting an external pressure on the gas.
- Water hammer and cavitation’s are the example of the importance of compressibility effects in liquid flows.
- Compressibility effects are very important in the design of modern high-speed aircraft, missiles, power plants, fans and compressors.
Key Takeaways:
It is the measure of elasticity in fluid. Fluids are compressed under pressure due to change in their mass density.
Bulk Modulus:
- It is the ratio of compressive stress to volumetric strain. It is denoted by 'K'.
Where, V = Volume of gas enclosed in cylinder
Dv = Change in volume,
Dp = Change in pressure
- Negative sign indicate decrease in volume with an increase in pressure.
- Value of K: Water is 2.05 x 10 N/m², Air is 1.02 x 10³ N/m
We know, Density (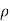
) = Mass /Volume=m/v …(1)
Since the mass m of a certain volume V is constant, differentiate Equation (i),
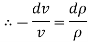
But bulk modulus
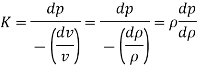
Key Takeaways:
It is the ratio of compressive stress to volumetric strain. It is denoted by 'K'.
Classification of Fluids is as follows:
- Newtonian Fluid (Fluid Mechanics)
- Non-Newtonian Fluid (Rheology)
- Pseudo plastic Fluid or Shear Thinning Fluid
- Dilatant Fluid or Shear Thickening Fluid
- Bingham Plastic Fluid or Ideal Plastic Fluid
- Thixotrophic Fluid or Plastic Fluid
- Ideal Fluid.
Newtonian Fluid (Fluid Mechanics)
- The Newtonian fluid is the fluid in which the shear stress is directly proportional to the rate of shear strain or velocity gradient
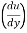
- All gases are Newtonian fluids. E.g.: Glycerin, kerosene. Air, water, alcohol etc.
- The linear relationship between shear stress and the rate of deformation is called as Newtonian fluid.
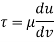
Non-Newtonian Fluid (Rheology)
- The fluid in which the shear stress is not directly proportional to the rate of shear strain or Velocity gradient, is called as Non-Newtonian Fluid.
- e.g., Slurries, tooth paste, gels, polymer solution paint, lubricant oils.
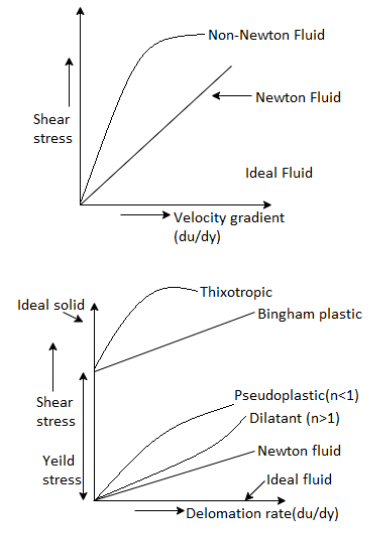
Fig 10: Variation of shear stress with velocity gradient
- The non-linear relationship between shear stress and the rate of deformation is called as Non- Newtonian fluid.
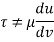
Pseudo plastic Fluid or Shear Thinning Fluid:
- Fluid in which the apparent viscosity decreases with increasing deformation rate (n< 1) is called as Pseudoplastic fluid.
- Examples are slurries, mud, polymer solution, quick sand, gums, blood, milk, colloidal suspensions paper pulp in water, ketchup.
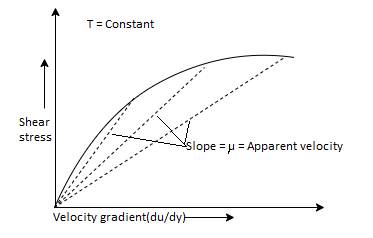
Fig: 11
Dilatant Fluid or Shear Thickening fluid:
- Fluid in which the apparent viscosity increases with increasing deformation rate (n>1) is called as dilatant fluids.
- e.g., Suspension of sand, starch, butter, sugar solution.
Bingham Plastic Fluid
- The fluid which possesses a definite yield stress but then the relationship between shear stress and angular deformation is linear is called as Bingham plastic fluid.
- e.g., Sewage sludge, tooth paste, oil paint, jellies, applesauce, drilling mud.
Thixotrophic Fluid or Plastic Fluid:
- The fluid which possesses a definite yield stress but then the relationship between shear stress and angular deformation is nonlinear are called as Thixotrophic fluid. e.g., Printer ink, lipstick.
Ideal Fluid:
- The fluid which has zero viscosity er shear stress is always zero is called as ideal fluid, that's why ideal fluid is represented by the horizontal axis.
Key Takeaways:
Classification of Fluids is as follows:
- Newtonian Fluid (Fluid Mechanics)
- Non-Newtonian Fluid (Rheology)
- Pseudo plastic Fluid or Shear Thinning Fluid
- Dilatant Fluid or Shear Thickening Fluid
- Bingham Plastic Fluid or Ideal Plastic Fluid
- Thixotrophic Fluid or Plastic Fluid
- Ideal Fluid.
- It is defined as the normal surface force acting per unit area.
- It is denoted by 'p' S.I. Unit N/m2 i.e., Pascal
P=force/Area
- When a fluid is contained in a vessel, it exerts force at all points on the sides and bottom of the container. The force per unit area is called as pressure.
- The pressure of a fluid on a surface will always act normal to the surface.
- Pascal law states, "The intensity of pressure at a point in a fluid at rest is same in all direction. Consider an arbitrary fluid element of wedge shape in a fluid mass at rest as shown in Fig.
Let the width of the element be unity.
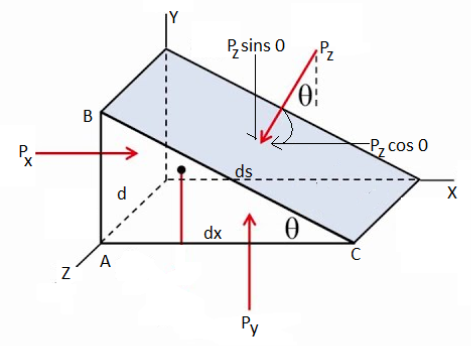
Fig: 12
Let px, py, and pz, be the pressures acting on the face AB, AC and BC respectively.
Let ∠ABC=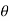
. Forces acting on the element are
Force on the face AB =Pressure in x-direction X Area of face AB
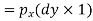
Force on the face AC = Pressure in y-direction x Area of face AC
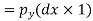
Force on the face BC= Pressure in z-direction x Area of face BC
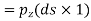
Weight of the element =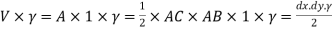 
Consider the triangle ABC as shown in Fig.
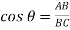
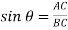
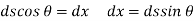
Resolve the force in x-direction we get
….(1)
Resolve the forces in y-direction
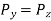…(2)
From Equations (i) and (ii),
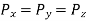
- Since the choice of fluid element was completely arbitrary, which means the pressure at any point is same in all direction. Pascal's law states that, “The pressure or intensity of pressure at a point in a static fluid is same in all direction."
- It is used for the construction of machines such as hydraulic press, hydraulic riveter etc. in which by the application of relatively small forces considerably larger forces are developed.
Key Takeaways:
Pascal's law states that, "The pressure or intensity of pressure at a point in a static fluid is same in all direction."
- The compressibility of a fluid is a degree of the relative extent alternate in reaction to a strain alternate. It is described irrespective of whether or not or now no longer this fluid is flowing due to the fact that it's far a thermodynamic function of that fluid.
- On the alternative hand, the compressibility of a glide is immediately associated with the fee of the Mach quantity withinside the glide. One can display that 2nd order Taylor decomposition of the momentum equation results in a time period for fluctuating strain that scales as M2. As a consequence, you can take into account that the glide is incompressible so long as the Mach quantity is decrease than 0. Three irrespective of the fluid at hand. In the case M=0.three, the "acoustic" fluctuating strain (that is how is frequently referred to as this 2nd order time period in strain) correspond to 10% of the convective (or aerodynamic) strain time period.
- The Atmospheric air exerts a normal pressure upon all the surfaces with which it comes in contact, is called as atmospheric pressure.
- The atmospheric pressure varies with the altitude and it can be measured by means of a barometer. It is also called as barometric pressure.
- There are two types of barometers i.e., Mercury barometer and Aneroid barometer.
- At sea level, under normal atmospheric condition at 15°C, the equivalent values of atmospheric pressure are 101325 N/m or 10.33m of water or 76 cm of mercury.
1 atm = 10.33 m of water = 1.01325 bar
P = 
.h=9.81 x 10.3= 101.325 kN/m2 or kPa
Key Takeaways:
The Atmospheric air exerts a normal pressure upon all the surfaces with which it comes in contact, is called as atmospheric pressure.
- The pressure, which is measured with reference to absolute vacuum pressure or zero pressure, is called as Absolute pressure.
- The pressure, which is measured above the atmospheric pressure, is called as gauge pressure. It is measured with the help of pressure measuring instruments.
- The pressure, which is measured below the atmospheric pressure, is called as vacuum pressure or negative gauge pressure.
- It is measured with the help of pressure measuring instruments. The relationship between the absolute pressure, gauge pressure and vacuum pressure are shown in Fig.
- Mathematically
- Absolute pressure =Atmospheric pressure + Gauge pressure
Pats =Patm+Pgauge
2. Vacuum pressure =Atmospheric Pressure-Absolute pressure
Pabs=Patm-Pvaccum
Key Takeaways:
The pressure, which is measured below the atmospheric pressure, is called as vacuum pressure or negative gauge pressure
The different types of manometers are listed below:
U-Tube Manometer:
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Furthermore, gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.
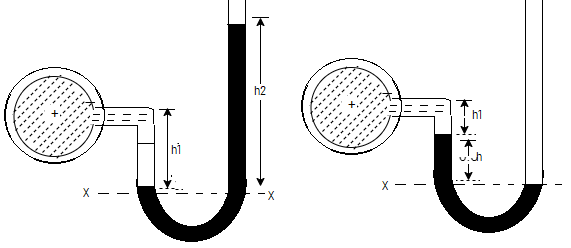
Fig 13: U-tube manometer
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb=
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1
Examples:
Q. A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km
Soln.:
Oil
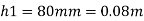
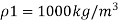
Mercury
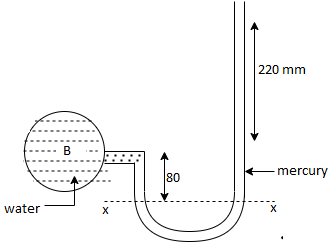
Fig: 14
Pressure in the left limb about xx = Pressure in the right limb about x-s
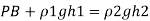
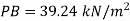
Q. A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury March 2010,7 Marks
Soln.:
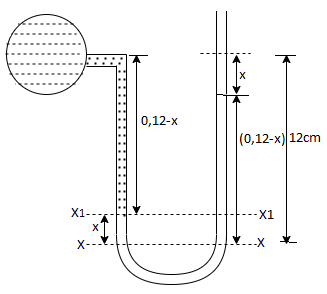
Fig: 15
Case I:
Given:
h1, =h₂= 12cm=0.12 m.
S2=13.6
Pressure in pipe
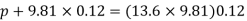
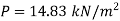
Case II:
Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.
Let x = rise of mercury in left limb= fall in mercury in right limb,
Pressure at new section x₁ - x₁
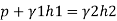
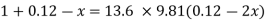
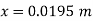
New difference of mercury
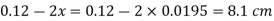
Q. Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
Soln:
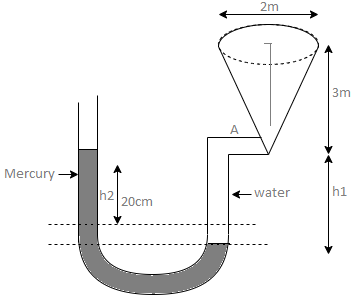
Fig: 16
Case I:
Vessel is empty
Pressure in left limb about x-x= Pressure in right limb about x-x
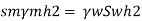
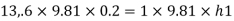
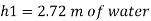
Case II: Vessel is full of water
When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m
Now consider 7-7 as a datum
Pressure in left limb = Pressure in right limb about z-z
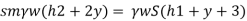
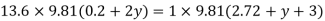
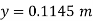
:. Difference of mercury level when the vessel is full of
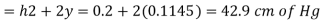
Key takeaways:
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Furthermore, gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
Single Column Manometer:
- This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
Due to inclination the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
Alpha = inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin
h = l sin alpha × S2 - h1S1
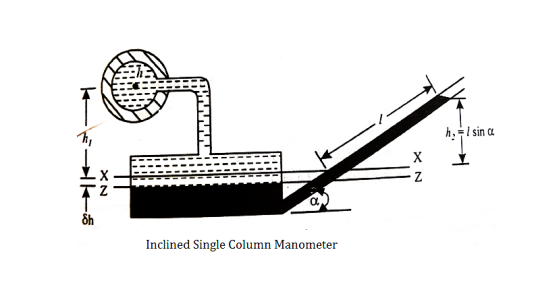
Fig 17: Single column manometer
Key takeaways
- This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
U-Tube Differential Manometer:
- A U-tube differential manometer is shown in fig.
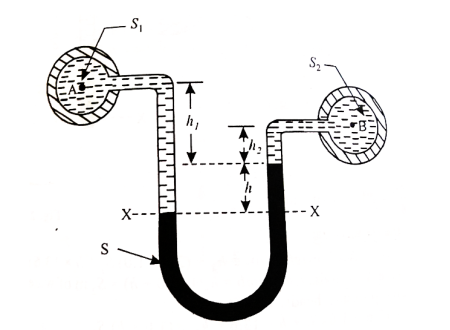
Fig 18: U-tube differential manometer
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
HA = pressure head at A,
HB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
h A + (h 1 + h) S1
Pressure head in the right limb:
h B + h 2 × S 2 + h × S
Equating the above pressure heads, we get
h A + (h1 + h) S1 = h B + h 2 × S 2 + h× S
(h A - h B) = h 2 × S 2 + h × S - (h 1 + h) S 1
Examples:
Q.A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer. Dec. 2015, 6 Marks
Sol:
Pipe A
S₁ = 1.6
PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²
h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)
Pipe B
s2= 0.8
h2= 1.5+h
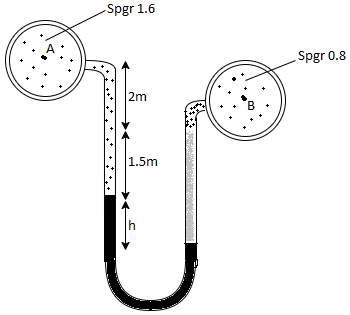
Fig: 19
Pressure in left limb = pressure in right limb PA
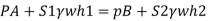
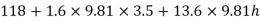
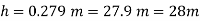
Q. A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m. Dec. 2009, 3 Marks
Soln.:
Given:
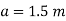
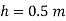
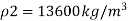
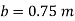
To find:
PA-PB
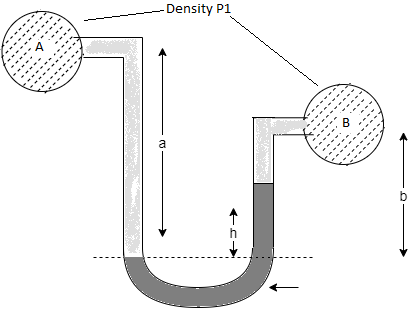
Fig: 20
Pressure in left limb = Pressure in right limb
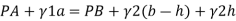
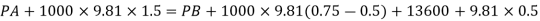
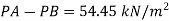
Q. Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6? Liquid level in the limb attached to A is lower than that in the order.
Soln.:
Given:
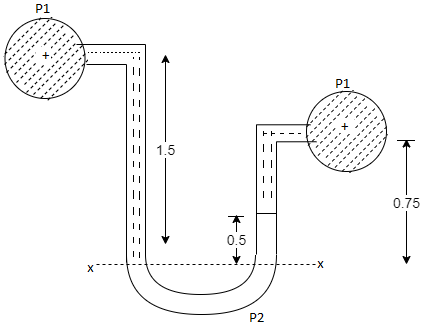
Fig: 21
1 1bar = 10^5 N/m²,
2 P=0.5 bar = 50 kN/m².
3 pB= 0.25 bar 25 kN/m²
Balancing the liquid about x-x in left limb and right limb
Pressure in left limb about x-x= Pressure in right limb about x-x
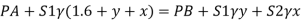
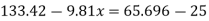
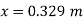
Key takeaways
- The final equation to calculate pressure from u tube manometer is
(h A - h B) = h 2 × S 2 + h × S - (h 1 + h) S 1
Micromanometers:
- A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
- One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.
- First of all, both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).
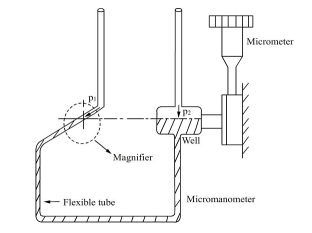
Fig 22: Micromanometer
Key takeaways:
A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
Pressure on Plane surface:
A pressure diagram is the graphical representation of the variation in the intensity of pressure over a surface. It is used to calculate total pressure force and centre of pressure for submerged body.
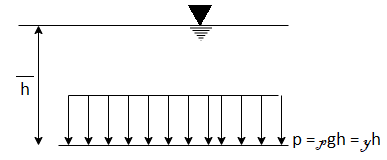
Fig 23: Pressure diagram for horizontal surface
Fig 24: Pressure diagram for inclined surface
1.19.1 Force on a vertical submerged plane surface:
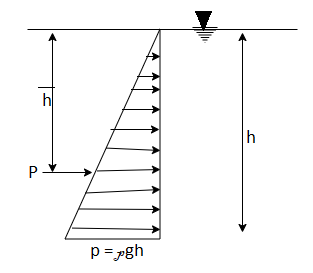
Fig 25: Pressure diagram for vertical surface
Centre of pressure by principle of moment,
P
=
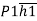+P2
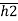+P3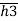
- The tendency of fluid to uplift a submerged body, due to the upward thrust of the fluid is known as buoyancy or force of buoyancy.
- It is always equal to the weight of fluid displaced by the body.
Centre of Buoyancy:
- The point at which the force of buoyancy is act is called as centre of buoyancy.
- It always lies C.G. Of the volume of the liquid displaced.
Fig 26: Centre of Buoyancy
- Where, H is the height of body. h is submerged height of block i.e., depth of immersion.
Floatation:
- It states that, "The weight of the body is equal to the buoyant force."
Buoyant force =Weight of body
FB = W
- Body existing in the liquid, the forces acting on the body are its weight (W) and buoyancy force (F). Whether the body sinks or floats, depends upon the magnitudes of W and FB.
- If W>FB, then the body sinks as shown in Fig.(a).
- If W = FB, then the body floats touching its top to the free surface of water as shown in Fig.(b).
- If W <FB, then the body floats as shown in Fig.(c).
Where FB = V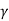
where V (volume of the body in the liquid) < the volume of complete body.
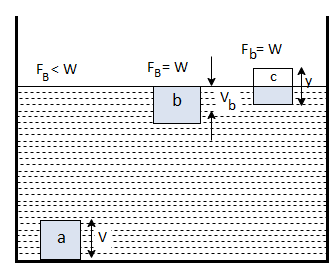
Fig 27
Key Takeaways:
The tendency of fluid to uplift a submerged body, due to the upward thrust of the fluid is known as buoyancy or force of buoyancy. It is always equal to the weight of fluid displaced by the body.
- The Archimede's principle states, "Whenever a body is immersed wholly or partially in a fluid, it is buoyed up (lifted up) by a force equal to the weight of fluid displaced by the body".
- Buoyant force = Weight of the fluid displaced by the body.
Stability of Floating Body:
Stable equilibrium
- When a body is given a smaller angular displacement due to external force and then it comes to its original position due to internal forces, is called as stable equilibrium.
- In stable equilibrium, metacentre is lies above centre of gravity, the metacentric height is positive.
- External couple is balanced by couple due to internal force.
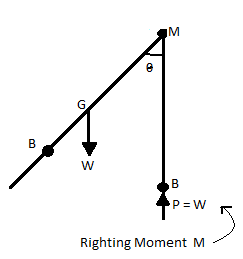
Fig 28: Stable equilibrium
Unstable equilibrium
- When a body does not return to its original position from the slightly displaced angular position and heels farther away, is called.us unstable equilibrium.
- In unstable equilibrium, metacentre M is lies below the centre of gravity G, the metacentre height is negative.
- External couple and couple due to internal force are in same direction. It is an unstable condition.
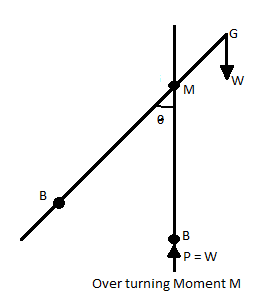
Fig 29: Unstable equilibrium
Neutral equilibrium:
- When a body is given a smaller angular displacement and set on new position, is called as neutral equilibrium.
- In neutral equilibrium, metacentre M and centre of gravity G are coincided.
Fig 30: Neutral equilibrium
Stability of Submerged Body:
- Condition of stability for submerged body are based on relative positions of centre of gravity G and centre of buoyancy B.
Stable equilibrium
- When centre of buoyancy is lies above the centre of gravity, submerged body is stable. (Refer Fig.(a)).
Fig: 31
Unstable equilibrium
- When centre of buoyancy is lies below centre of gravity, submerged body is in unstable equilibrium. (Refer fig.(b))
Neutral equilibrium
- When centre of buoyancy and centre of gravity is coincided, body is in neutral equilibrium. (Refer Fig.(c))
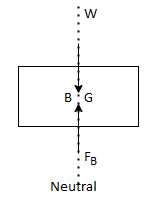
Fig: 32
Key Takeaways:
The three types of equilibrium are given in both case:
- Stable equilibrium,
- Unstable equilibrium
- Neutral equilibrium
- Let W1 is movable weight which is shifted by a distance x across the axis of tilt.
- Let
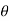is the angle of tilt. - Moment due to shifted load, M₁ = W₁. x
- The moment M1 is balance by moment due to self-weight
M₂ = W x GG1
∵
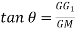
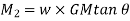
∴ For stable equilibrium. M₁ = M₂,
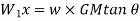
Metacentric height is, GM=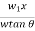
Time of oscillation is obtained by
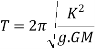
Where k = radius of gyration
Numericals:
Q. Density of liquid is 850 kg/m³. Determine relative density and weight density of the liquid. With reason state whether the liquid will float on water or not
Soln.:
Gives:
p= 850kg/m'.
P. 1000kg/m (standard value)
To find: Relative density, weight density
Relative density
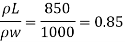
Weight density
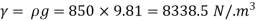
The liquid will float on water because weight density of liquid is less than water.
Q. On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.
Soln.:
Given:
Weight W= 12 N.
Mass m = 4.893 kg
Weight = Mass x acceleration
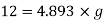
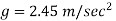
Acceleration due to gravity on a certain planet is 2.45 m/sec.
Q. What is the specific volume of material with specific gravity 0.87
Soln.:
Given:
Specific gravity=0.5,
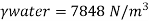
To find: Specific volume.
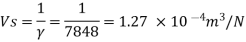
Q. The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.
Soln.:
Given:
Specific volume =0.7
To find: Mass density, specific weight
Mass density (p)
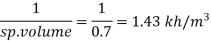
Specific weight (Y)
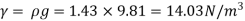
Q. Calculate the specific weight, density, specific volume and relative duty of oil which 7 N per liter.
Soln.:
Given:
Weight W=7N,
Volume V= 1 litre = 10^-3 'm^3
To find:
Specific weight,
Specific volume,
Relative density
Specific weight Y
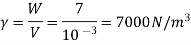
Density
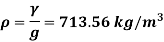
Specific volume (Vs)
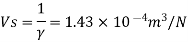
Relative density
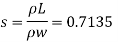
Q. Liter of petrol weighs 14N. Calculate the specific weight, density, specific volume and specific gravity of petrol with respect to water.
Soln.:
Given: V=2 liter = 2 x 10-3m,
W=14N
To find:
- Specific weight,
- Density,
- Specific volume
- Specific gravity.
- Specific weight
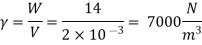
Specific weight = Mass density x Acceleration due to gravity
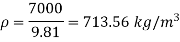
2. Specific volume (V)
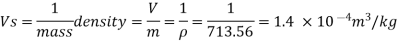
3. Specific gravity (S)
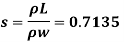
Q. A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.
Soln.:
Given:
Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3
Weight W=9N
To find: Weight density, specific gravity
- Weight density (Y) =
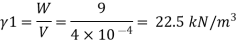
2. Specific gravity
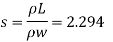
Q. Calculate the gauge pressure and the absolute pressure within:
(1) a droplet of water 0.3 cm in diameter
(2) a jet of water 0.3 cm in diameter.
Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec.
Soln.:
Given:
d = 3mm = 3 x 10³ m.
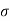water = 0.073N/m.
Patm = 101.3 N/m² atm
For droplet and air bubble
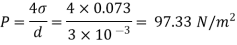
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²
For jet
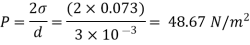
Absolute pressure in jet
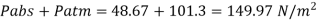
Q. Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.
Soln.:
Given:
P-130 N/m²
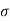= 7.26×10^-2 N/m
For droplet, P
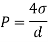
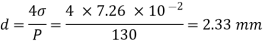
The diameter of a droplet of water is 2.33 mm
Q. In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given: -
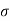= 0.07 Nm.
D= 001mm= 0.01 = 10 m
An air bubble has only one surface,
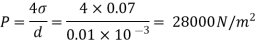
The pressure difference between inside and outside of an air bubble is P= 25000N/m2
Q. Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm
Soln.:
Given:
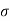= 0.1Nm,
d=50x10^-3 mm
For soup bubble, P
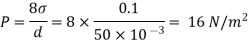
The pressure inside a soup babble is 16 N/m2
Q. If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given:
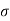water = 0.075N/m,
d=0.01mm
An air bubble has only one surface,
The pressure difference between inside and outside of an air bubble is P=30000N/m2
Q. What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.
Soln.:
Given: -
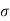= 0.0725 N/m,
D= 5 cm = 0.05m
Force required to lift a than wire ring
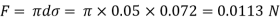
Q. A 10 mm glass tube is inserted into trough containing mercury. Find the capillary effect when the contact angle is: () 180 and (0) 110 Take surface tension of mercury in contact with air as 0.51 N/m.
Soln.:
Given: d = 10 mm= 10 x 10 m,
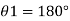
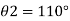
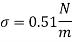
For mercury p=13600 kg/m²
To find: Capillary effect
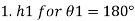
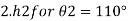
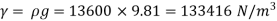
1) Case 1: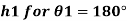 
Weight density for mercury
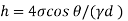
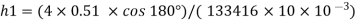
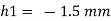
Negative sign indicates capillary depression.
2) Case 2: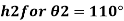 
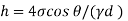
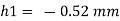
Negative sign indicates capillary depression
Q. Two wide clean glass plates are held parallel with a gap of 1mm between them. What will be the rise of water level between these plates when dipped in water? Assume surface tension for water as 0.0730 N/m.
Soln.:
Given:
t=gap=1 mm
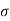=0.073 N/m
For two wide clean glass plates, 
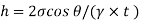
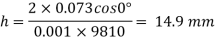
Capillary rise is 14.9 mm.
Q. A clean tube of internal diameter 3 mm is immerged in a liquid with a coefficient of surface tension 0.48 N/m. Angle of contact of the liquid with the glass can be assumed to be 130%. The density of the liquid is 13600 kg/m". What would be the level of the liquid in the tube relative to the free surface of the liquid outside the tube?
Soln.:
Given:
d= 3 mm,
= 0.48 N/m
The capillary rise (or depression) is given as
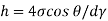
For mercury = 130°.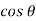 
=-0.6428
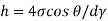
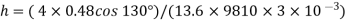
h= - 3. 083 mm
The negative sign indicates that there is capillary depression.
Q. Find the height through which water rises by capillarity action in a glass tube of 2 mm bore, if the surface tension at the prevailing temperature is 0.0736 N/m. Assume angle of contact of glass with water -0°
Soln.:
Diameter of glass tube d=2 mm=2x10-3 m
Surface tension=0.0736 N/m
Angle of Contact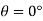 
Capillary rise
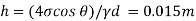
h= 15 mm
The height by which water rises by capillary is 15 mm.
Q. A glass tube of internal diameter 0.2 mm is immersed in mercury. The angle of contact of mercury with glass can be taken as 130 W lat will be the level of Hg in the tube relative to the free surface of the liquid outside the tube? Take surface tension of liquid = 0.5 N/m Dec.
Soln.:
Given: d= 0.2mm,
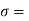0.5 N/m
The capillary rise (or depression) is given as
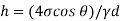
For mercury
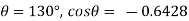
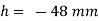
The negative sign indicates that there is capillary depression.
Q. Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air as 0.0735 N/m.
Soln.:
Given:
h=0.25 mm,
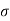=0.0735 N/m,
To find: Minimum size of glass tube 'd'.
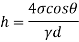
For water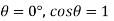 
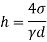
Q. State the minimum diameter of glass tube to be immersed in water, for which capillarity effects are to be limited up to 2.08mm Take surface tension of water in contact with air as 0.073 N/m.
Soln.:
Given:
h=298mm,
=0.073 N/m,
for glass plates
To find: Diameter of tube,
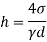
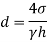
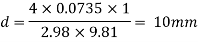
The diameter of glass tube immersed in water is 10 mm.
Q. A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.
Soln.:
Given: Distance between plates
Dy= 0.02 mm = 0.02 x 10-3 m
Velocity of upper plate u 60 cm/s 0.6 m/s
Change in velocity du=u-0-0.6 m/s.
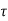= Force per unit Area = 3 N/m²
To find: Viscosity
Using Newton's law of viscosity
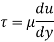
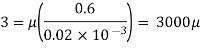
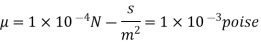
The fluid viscosity between the plates is 1 x 10-3 poise,
Q. A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise
Soln.:
Given:
A=2.5 x 10 mm²=2.5m²,
Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,
=1 poise = 0.1N-s/m
To find: Force, power
Using Newton's law of viscosity:
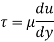
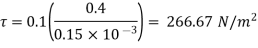
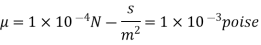
As we known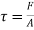 
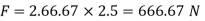
Power required to move the plate at speed 0.4 m/s
= Force x Velocity = 666.67 x 0.4 N-m/
1 N-m/s = 1 Watt
P = 266.67 Watt
Power required moving the plate is 266.67 Watt.
Q. The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks
Determine:
(1) The dynamic viscosity of oil.
(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95
Solution:
Square plate of side, a = 720 mm=0.72 m
Thickness of oil film, t = 15 mm= 15 x 10
Velocity of plate v= du= 3m/s
Force F= 120 N
Specific gravity s= 0.95
To find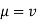 
Mass density,
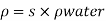
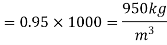
Area of plate,
A= 0.72x0.72 = 0. 5184 m²
Using Newton's law viscosity
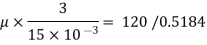
Dynamic viscosity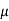 
= 1.157 N/m²
Kinematic viscosity, v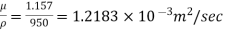 
Q. A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness
Soln.:
Given:
Area A = 0.2 m²
Weight of late W = 500 N
Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N. s/m² = 0.981 N-s/m²
To find: Thickness of film.
Component of W along the plate W sin 8= 500 sin 30= 250 N
Shear force on the bottom surface of the plate
F = 250N
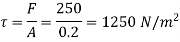
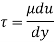
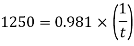
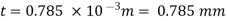
The lubricant film thickness is 0.785 mm
Q. A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.
Soln.:
Given:
Area A = 12x04 0.48 m²
Weight of plate W =970 N
Velocity of plate u = 2.25 m/sec
Thickness of film t = dy = 2 mm = 2 x 10³ m
To find: Viscosity
Component of W along the plate= W sin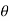 
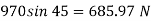
Shear force on the bottom surface of the plate
F= 685.89 N
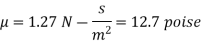
The viscosity of the liquid is 12.7 poise.
Q. Determine the Bulk modulus of elasticity of a liquid, which is compressed in a cylinder from a volume of 0.0125 m³ at 80 N/cm² pressure to a volume of 0.0124 m³ at 150 N/cm² pressure?
Soln.:
Given:
Initial volume V = 0.0125 m²,
Final volume = 0.0124 m³
DV = Decreases in volume = 0.0125 -0.0124 = 0.0001m³
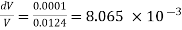
Initial pressure = 80 N/cm2
Final pressure - 150 N/cm
Increases in pressure = 150-80= 70 N/cm = 70 x 10^4 N/m²
Bulk modulus K
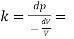Change in pressure/ (change volume/ original volume)
The Bulk modulus of elasticity of a liquid is 56.79 x 10^6 N/m2
Q. Determine the Bulk modulus of elasticity of a liquid, if the pressure of the liquid is increased from 400 Pa to 1200 Pa. The volume of the liquid decreases by 0.15%.
Soln.:
Given:
Initial pressure 400 Pa,
Final pressure 1200 Pa,
DV = 0.15% V
Increases in pressure
Decreases in volume
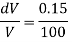
Bulk modulus
Q. A cylinder contains a liquid of volume of 0.02 m' at pressure of 700 Pa when compressed to reach a volume of 0.019 m The pressure is increased to 1400 Pa. Find bulk modulus of elasticity.
Soln.:
Given:
Initial volume 0.02 m²
Final volume 0.019 m
Change in volume dv=0.02- 0.019 = 1x 10^-3 m^3
Change in pressure dp = 1400-700 = 700 Pa
Bulk modulus k
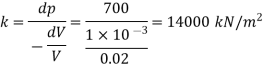
Q. If the bulk modulus of elasticity of water is 2.07 x 10° kN/m²:
(1) What is the pressure required to reduce its volume by 2%?
(ii) What will be the change in mass density?
Soln.:
Given:
K=207 x 10 kN/m²
DV/V= 2%
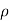for water = 1000 kg/m
To find: dp, d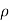
1) Pressure required to reduced its volume by 2%
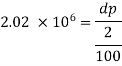
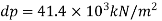
2) Change in mass density
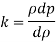
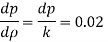
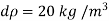
Q. A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.
Soln.:
Given:
Pressure p= 1.2M,
Pascal = 12x10 N/m².
Volume V 650 liter= 650 x 10³ m.
Reduction in volume dV= 1.5 liter= 1.5 x 10^-3 m3
Bulk modulus of elasticity, K
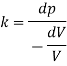
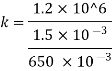
Compressibility
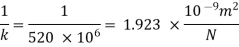
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.
Q. At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:
a) The change in specific volume between the surface and the given depth
b) Specific volume at the given depth and
c) Specific weight at that depth.
Soln.:
Given:
Pressure dp = 480 kg/cm²
Average modulus of elasticity K = 24 x 10' kg/cm
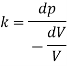
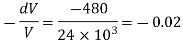
Specific volume of the water at the surface of the ocean,
Specific volume
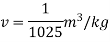
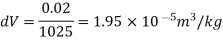
Specific volume at the depth of 5 km,
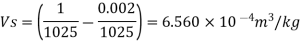
Specific weight of water at the depth of 5 km,
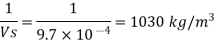
Q. At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. For that pressure range.
1) What will be the change in specific volumes between that at the surface and at that depth?
2) What will be the specific volume at that depth?
3) What will be the specific weight at that depth?
Soln.:
Given:
P₁ = 840 x 10¹ Pa,
H1, = 2 km = 2000 m.
= 10250 N/m²,
K = 2.4 x 10' Pa
Bulk modulus K
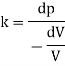
And 
Specific volume
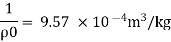
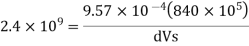
Change in specific volume
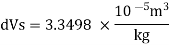
Specific volume at 2 km depth
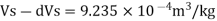
Density at 2 km depth
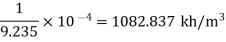
Specific weight
Q. A closed tank of height 9.0 m is filled with bromine of specific gravity 3.1 to a depth of 2 m and turpentine of specific gravity 0.87 to a depth of 6m. The upper part of the tank contains air under a pressure of 25 kPa (vacuum). Find the absolute pressure at the bottom of the tank in kPa and in cm of mercury Neglect density of air. Consider atmospheric pressure 101.3 kPa
Soln.:
Given:
Fig: 33
Atmospheric pressure
Patm= 101.3 kpa
Air pressure P=25 kPa (vacuum)
Gauge pressure at bottom of tank
= Air pressure + pressure due to turpentine + pressure due to bromine
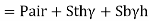
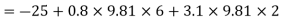
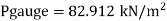
Absolute pressure
Pressure head in term mercury
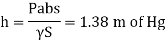
Q. The tank shown in Fig. P. Is closed at to and contains air at a pressure of P, Calculate the value of P, for the manometer reading as shown in Fig.
Soln.:
Given:
h₁ = 10 cm = 0.1 m,
h₂ = 150 cm= 15m
h3 = 200+10-150=60 cm=0.6 m
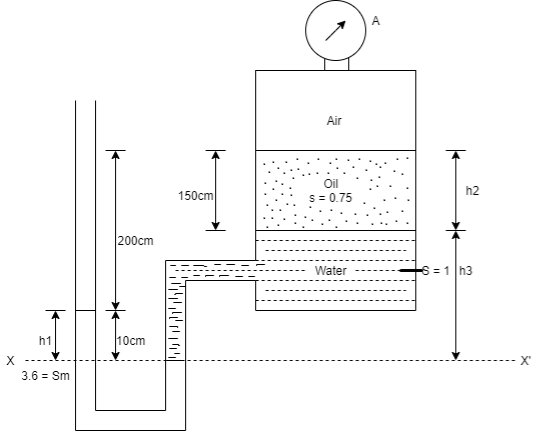
Fig: 34
Consider section X-X, balance the fluid about X-X.
Pressure on left limb about XX= Pressure on right limb about X-X
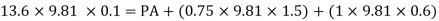
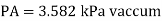
References:
1. Fluid mechanics and machinery R Berndtsson and P.N. Chadramouli
2. Hydraulic and fluid mechanics, PM Modi and SM Seth
3. Theory and applications of fluid mechanics, K Subramanya, Tata McGraw Hill
4. Fluid mechanics with engineering applications, RL Daughterty, JB Franzini
