Module-5
Fourier series
Periodic functions-
If the value of the function (y-axis) repeats itself on x-axis, then the function is called periodic function.
Suppose f(x) is a function, then
If f(x) = f(x + t) = f (x + 2t) = …………….
Then t is called the periodic of the function f(x).
Suppose of we take sin x, then it repeats its value after the period of 2 such that, we write this as
such that, we write this as
Sin x = sin (x + 2 sin ( x + 4
sin ( x + 4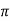 ) ………….
) ………….
We can say that sin x is a periodic function with the period of 2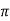
Note-
A series of the form,

Is called fourier series , where
 are constants.
are constants.
Any periodic function can be expanded in the form of fourier series.
Determination of 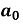 ,
, 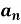 ,
, 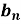 of Fourier series-
of Fourier series-
We know that, the fourier series,
f(x) = 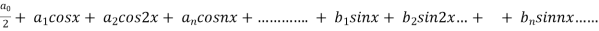 ------------ eq.(1)
------------ eq.(1)
To find 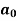 –
–
Intergrate equation (1) on both sides, from 0 to 2π
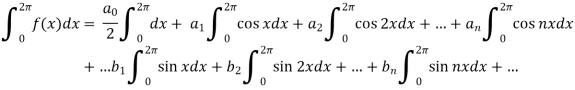
Which gives,
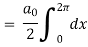
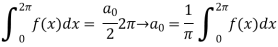
To find  -
-
Multiply each side of eq. (1) by cos nx and integrate from 0 to 2π
We get,
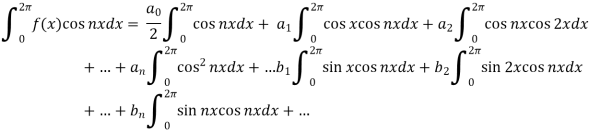
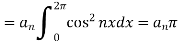
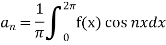
Similarly we can find 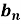 by, multiplying eq. (1) by sin nx and integrating from 0 to 2π
by, multiplying eq. (1) by sin nx and integrating from 0 to 2π
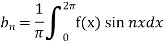
Example: Find the fourier series of the function f(x) = x where 0 < x < 2 π
Sol. We know that, from fourier series,
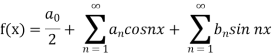
First we will find 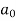 ,
,

Now, 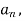
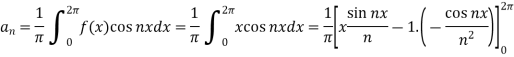
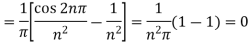
And  ,
,
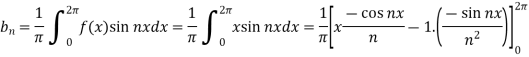
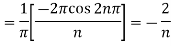
Put these value in Fourier series, we get

Example: Find the Fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
Sol. First we will find
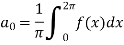
= 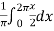
=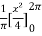
= π
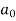 = π
= π
Similarly,
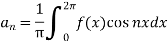
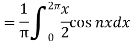
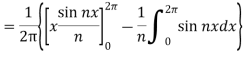

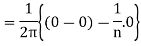
Which gives, 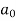 = 0
= 0
Now,
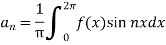

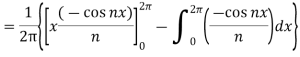
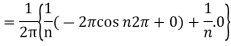

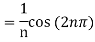
We get, 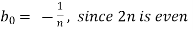
We know that, the Fourier series
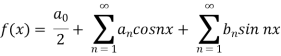
Put these values in Fourier series, we get
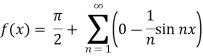
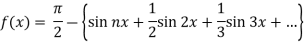
Example: Find the Fourier series for f(x) = 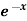 in the interval
in the interval 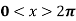 .
.
Sol.
Suppose
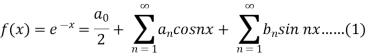
Then-
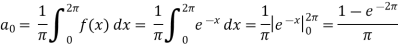
And
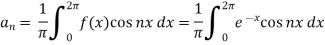
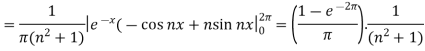
So that-

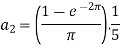
And then-
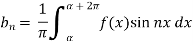
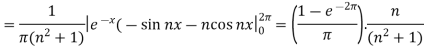
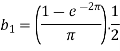
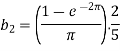
Now put these value in equations (1), we get-
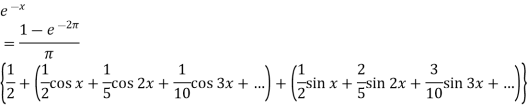
Key takeaways-

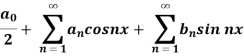
Is called fourier series , where
The Fourier series for the function f(x) in the interval 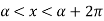 is given by-
is given by-

Here-
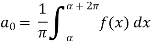
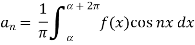
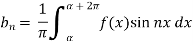
Where-
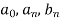 are called Euler’s formulae.
are called Euler’s formulae.
Example: Find the fourier series of the function f(x) = x where 0 < x < 2 π
Sol. We know that, from fourier series,
f(x) = 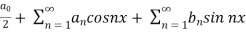
first we will find 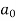 ,
,
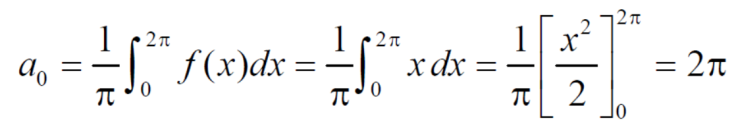
Now, 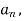
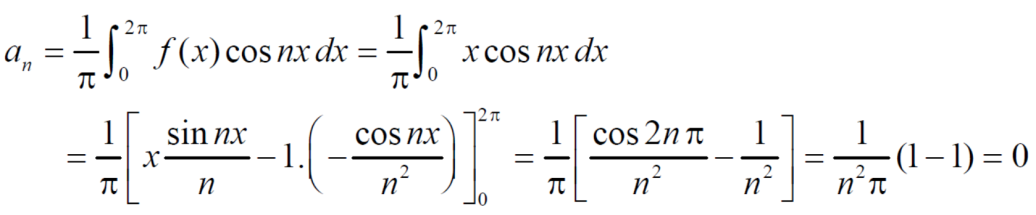
And  ,
,
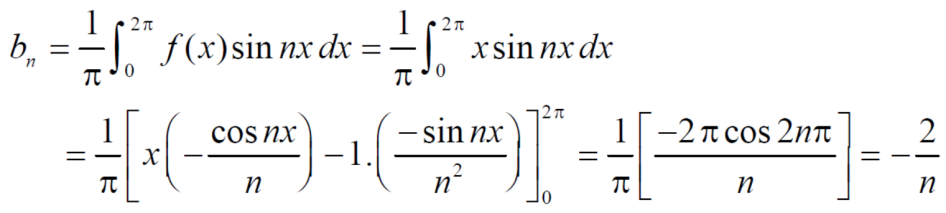
Put these value in fourier series, we get
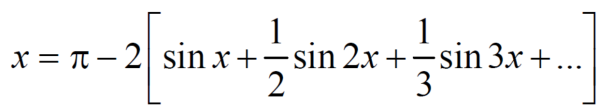
Example: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
Sol. First we will find
 =
= 
= 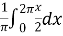
=
= π
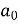 = π
= π
Similarly,
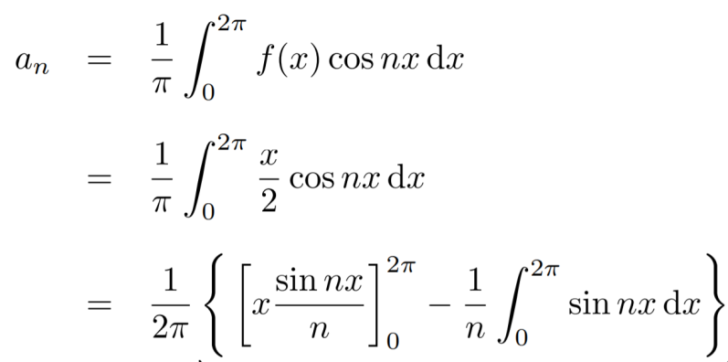
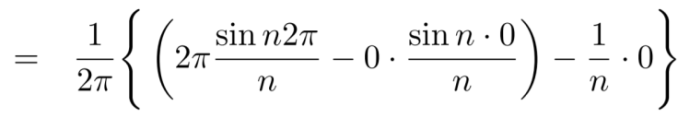
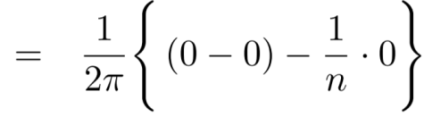
Which gives, 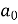 = 0
= 0
Now,
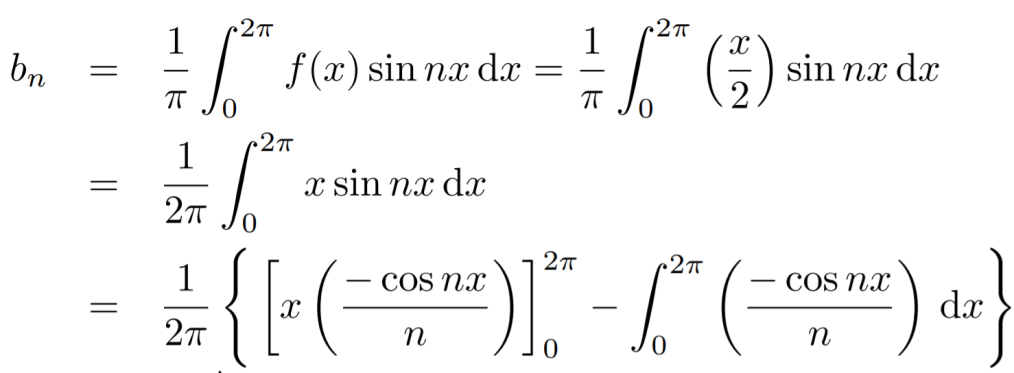
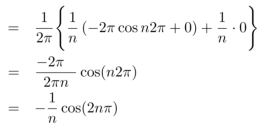
We get, 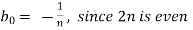
We know that, the fourier series
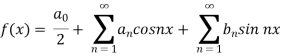
Put these values in fourier series, we get
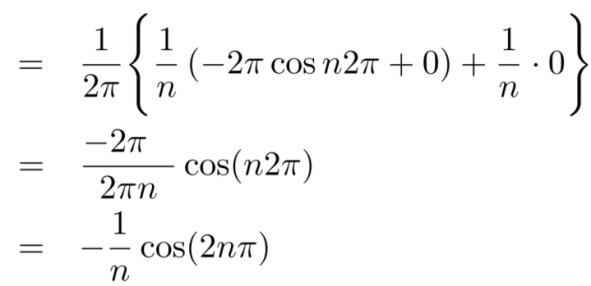
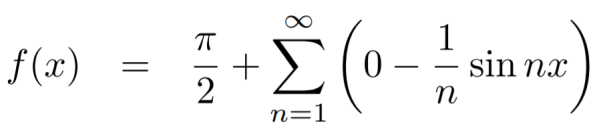
Example: Find the Fourier series for f(x) = 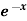 in the interval
in the interval 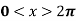 .
.
Sol.
Suppose
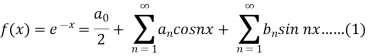
Then-
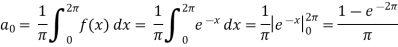
And
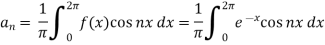
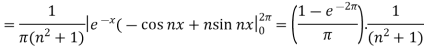
So that-
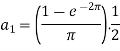
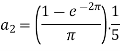
And then-
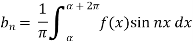
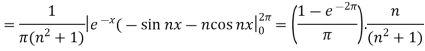
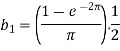
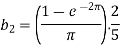
Now put these value in equations (1), we get-
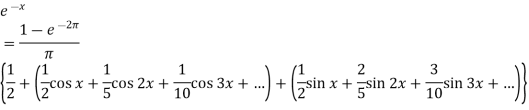
Key takeaways-
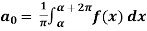
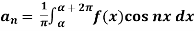
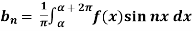
Odd function-
A function f(x), which is written as ,
f( - x ) = - f(x)
is known as odd function.
The graph of the odd function looks like-
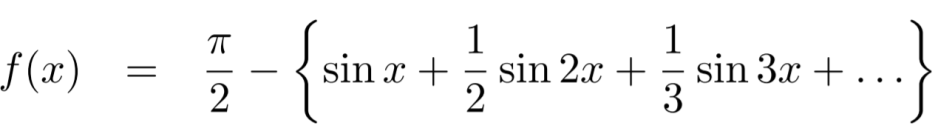
The graph of the function is symmetric about x-axis.
And the area under the curve from -π to π is always zero.(see fig)
Even function-
If f(-x) = f(x) then the function is known as even function.
The graph of the function f(x) looks like-

Area under the curve from -π to π will always be double the area from 0 to π

Expansion of an even function-
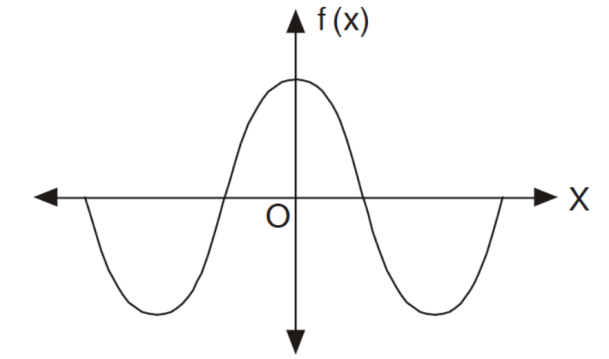
Here cosnx and f(x) are both even functions.
As we know that the product of two even numbers will be even.
Such as product of f(x) and cosnx will always be even.
Now,

Here we see that sin nx is an odd function.
So that we do not need to find 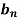
That means the series of an even function contains cosine terms only.
Expansion of an odd function-
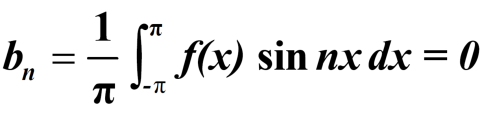
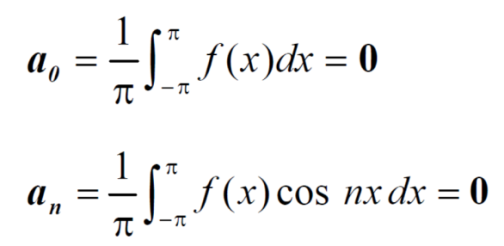
The series of the odd function contains only sine terms.
Example: Find the fourier expression of f(x) = x³ for –π< x <π.
Sol.
Here, we can see that f(x) Is an odd function
So that,
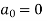 and
and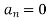
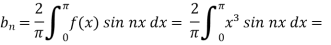
We will use here,
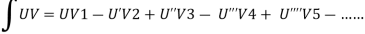
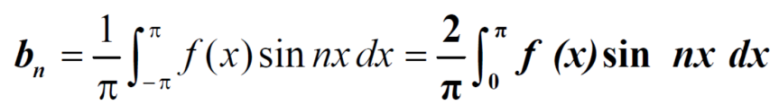
We get the value of f(x),
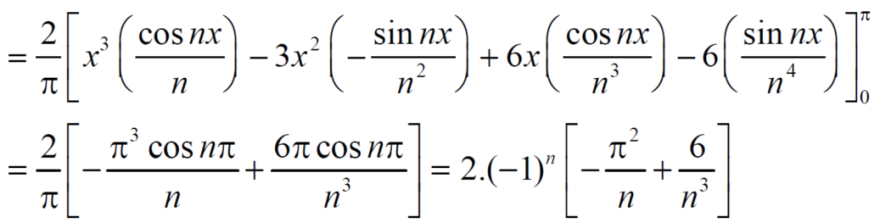
Example: Find the Fourier series expansion of the periodic function of period 2π.
f(x) = x² , -π≤x≤π
sol. The given function is even, so that,
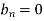
We will find 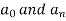
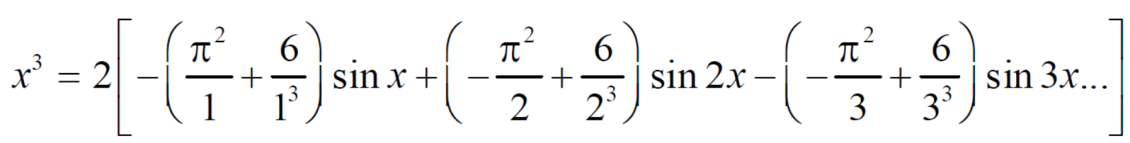
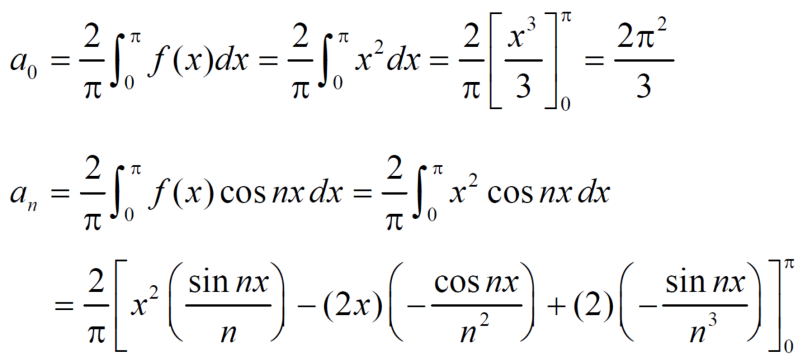
The fourier series will be ,

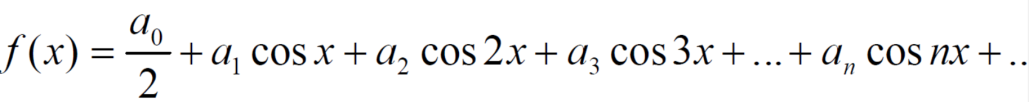
Key takeaways-
The function is defined in the interval (0,π) and it is immaterial whatever the function may be outside the interval (0,π)
to get the series of cosines only we suppose that f(x) is an even function in the interval (-π,π)
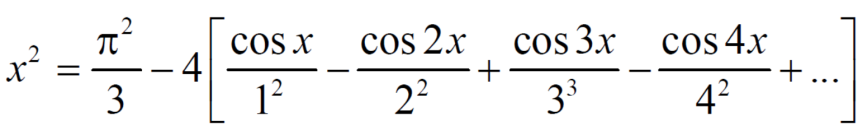
And bn = 0
To expand the as a sine series in the same interval and as an odd function.
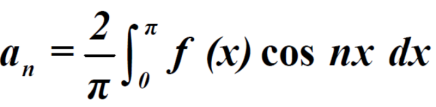
bn = 0.
Example- Find a Fourier series for
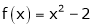 ;
; 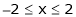
Solution:
Here
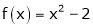 ;
; 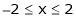
Since f(x) is even function hence 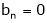
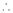 It’s Fourier series is
It’s Fourier series is
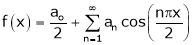 … (1)
… (1)
Where
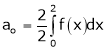
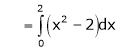
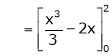
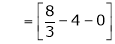
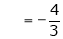
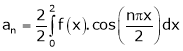
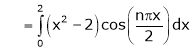
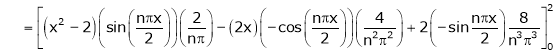
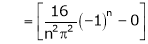
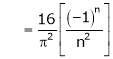
Hence equation (1) becomes,
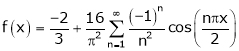
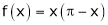
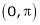
a) 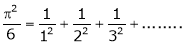
b) 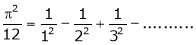
Solution:
Here
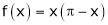 ;
; 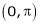
Hence it’s half range cosine series is,
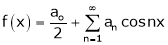 … (1)
… (1)
Where
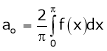
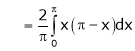
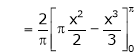
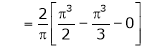
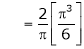
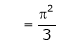
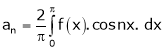
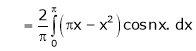
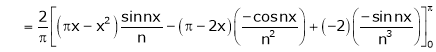
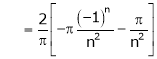
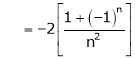
Hence equation (1) becomes,
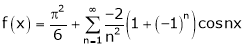
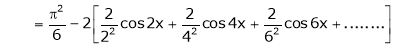
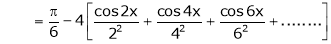 … (2)
… (2)
Put x = 0, we get
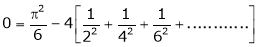
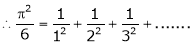
Hence the result
Put 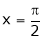 we get,
we get,
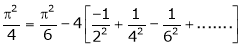
i.e. 
Example: Find the Fourier sine series for the function-
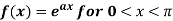
Where ‘a’ is a constant.
Sol. here we know-
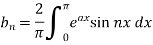
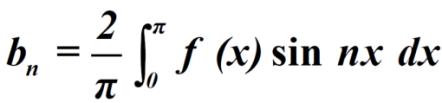
We know that-
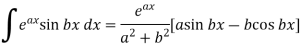
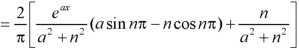
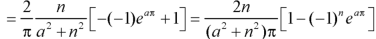
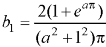
And
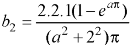
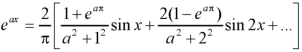
The Fourier integral of f(x) is-
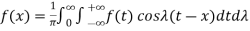 ………. (1)
………. (1)
Which can be written as-
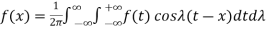 …………… (2)
…………… (2)
Because 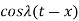 is an even function of
is an even function of  . Also since
. Also since 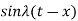 is an odd function of
is an odd function of 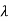 then we have-
then we have-
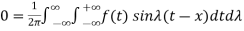 ……… (3)
……… (3)
Multiply (3) by ‘i’ and add to (2)-
We get-

Which is the complex form of the Fourier integral.
Example 1:
Using complex form, find the Fourier series of the function
f(x) = sinx = 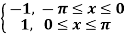
Solution:
We calculate the coefficients 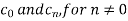
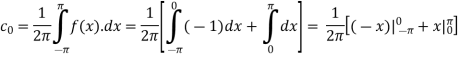
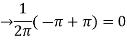
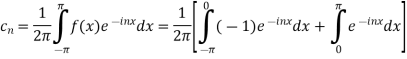
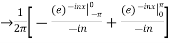 =
= 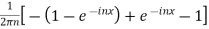
=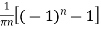
Hence the Fourier series of the function in complex form is
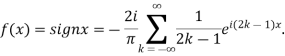
We can transform the series and write it in the real form by renaming as
n=2k-1,n=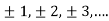
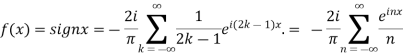
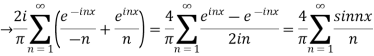
= 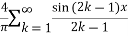
Example 2:
Using complex form find the Fourier series of the function f(x) = x2, defined on te interval [-1,1]
Solution:
Here the half-period is L=1.Therefore, the co-efficient c0 is,
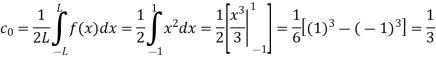
For n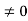
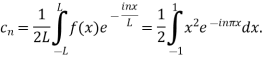
Integrating by parts twice,we obtain
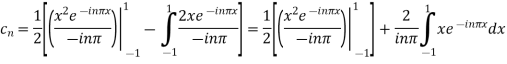
= 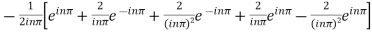
= 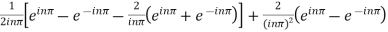
=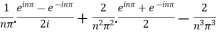 .
.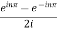
= 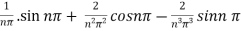 .
.
Fourier integral theorem-
Fourier integral theorem can be stated as-
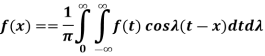
Proof: we have the Fourier series of a function f(x) in interval (-c, c) is-

And 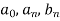 are given as-
are given as-
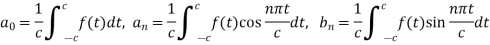
Put the values of 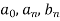 in equation (1), we get-
in equation (1), we get-
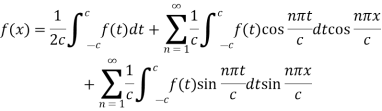
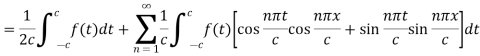
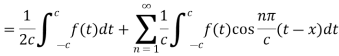
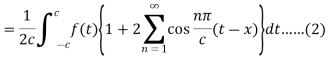
As we know that cosine functions are even functions, then-

Equation (2) reduces to-

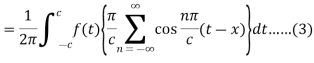
Here we will assume that c increases indefinitely, therefore we can take,
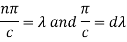
By this assumption, we get-
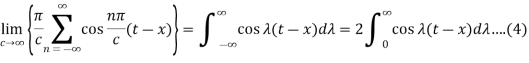
From equation (3) and (4), we get-

So that-
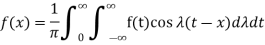
Example: 1
Find the fourier integral representation of the function
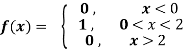
Solution:
The graph of the function is shown in the below figure satisfies the hypothesis of
Theorem -1 . Hence from Eqn,(5) and (6), we have
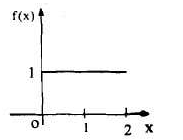

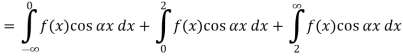
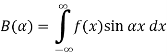
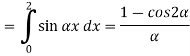
Substituting these coefficients in Eqn.(4) we obtain
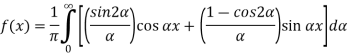
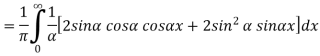
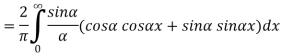
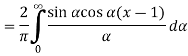
This is the Fourier integral representation of the given function.
Example: 2
Find the Fourier integral representation of the function
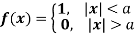
Solution:
The graph of the given function is shown in the below figure. Clearly, the given function f(x) is an even function. We represent f(x) by the fourier cosine integral . We obtain
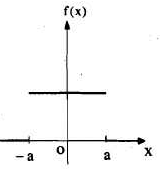
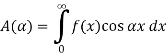
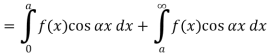

And thus,
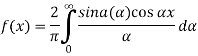
Fourier transform-
In mathematics, a Fourier transform (FT) is a mathematical transform that decomposes a function (often a function of time, or a signal) into its constituent frequencies, such as the expression of a musical chord in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time.
The Fourier transform of a function of time is a complex-valued function of frequency, whose magnitude (absolute value) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation, as proven by the Fourier inversion theorem
The function-
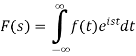
Is called the Fourier transform of the function f(x).
The function f(x) given below is called inverse Fourier transform of F(s)-
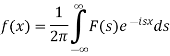
Properties of Fourier transform-
Property-1: Linear property- If F(s) and G(s) are two Fourier transforms of f(x) and g(x) respectively, then-
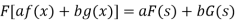
Where a and b are the constants.
Property-2: Change of scale- If F(s) is a Fourier transform of f(x), then
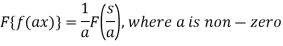
Property-3: Shifting property- If F(s) is a Fourier transform of f(x), then
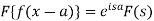
Property-4: Modulation- If F(s) is a Fourier transform of f(x), then

Example: Find the Fourier transform of-
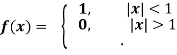
Hence evaluate 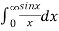
Sol. As we know that the Fourier transform of f(x) will be-
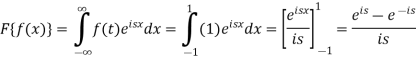
So that-

For s = 0, we get- F(s) = 2
Hence by the inverse formula, we get-

Putting x = 0, we get
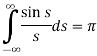
So-
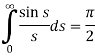
Example: Find the Fourier transform of 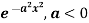
Sol. As we know that the Fourier transform of f(x) will be-
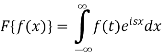
So that-
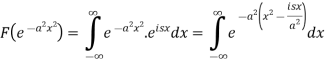
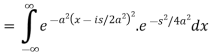
Now put 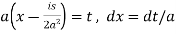
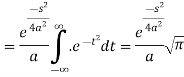
So that-
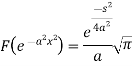
Key takeaways-
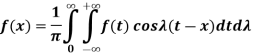
2. complex form of the Fourier integral-
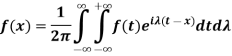
3. Fourier integral theorem-

4. The function-
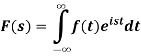
Is called the Fourier transform of the function f(x).
5. Linear property- If F(s) and G(s) are two Fourier transforms of f(x) and g(x) respectively, then-
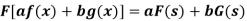
6. Change of scale- If F(s) is a Fourier transform of f(x), then
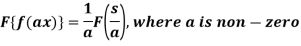
7. Shifting property- If F(s) is a Fourier transform of f(x), then
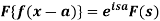
8. Modulation- If F(s) is a Fourier transform of f(x), then
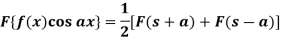
References