Module-2
Eigen values and eigen vectors
Characteristic equation: -
Let A he a square matrix, 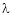 be any scalar then
be any scalar then 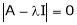 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘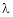 ’ be any scalar then,
’ be any scalar then,
1) 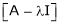 is called characteristic matrix
is called characteristic matrix
2) 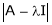 is called characteristic polynomial.
is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Eigen vector:-
Suppose 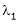 be an Eigen value of a matrix A. Then
be an Eigen value of a matrix A. Then 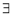 a non – zero vector x1 such that.
a non – zero vector x1 such that.
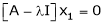 … (1)
… (1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value 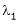 .
.
Properties of Eigen values:-
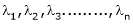

Properties of Eigen vector:-
Example1: Find the sum and the product of the Eigen values of 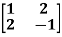 ?
?
Sol. The sum of Eigen values = the sum of the diagonal elements
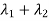 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
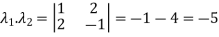
On solving above equations we get 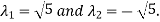
Example2: Find out the Eigen values and Eigen vectors of 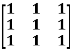 ?
?
Sol. The Characteristics equation is given by 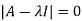
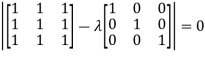
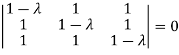
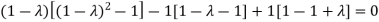
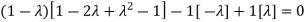
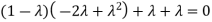
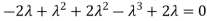
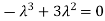
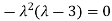
Or 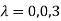
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 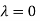 is
is
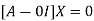
Where X is the column matrix of order 3 i.e.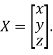
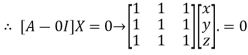
This implies that 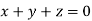
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 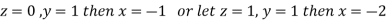
Thus the Eigen vectors corresponding to the Eigen value 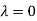 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 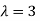 is
is
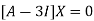
Where X is the column matrix of order 3 i.e.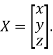
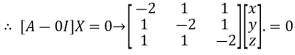
This implies that 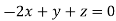
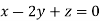
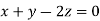
Taking last two equations we get
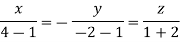
Or 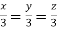
Thus the Eigen vectors corresponding to the Eigen value 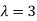 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 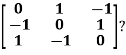
Sol: Let A =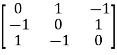
The characteristics equation of A is 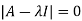 .
.
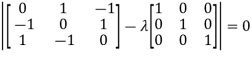
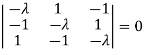
Or 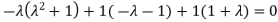
Or 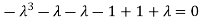
Or 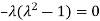
Or 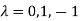
The Eigen vector corresponding to Eigen value 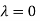 is
is
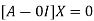
Where X is the column matrix of order 3 i.e.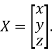
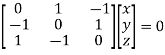
Or 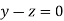
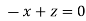
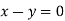
On solving we get 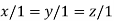
Thus the Eigen vectors corresponding to the Eigen value 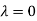 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 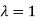 is
is
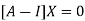
Where X is the column matrix of order 3 i.e.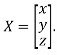
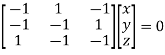
or 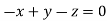
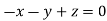
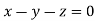
On solving 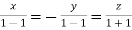 or
or 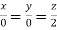 .
.
Thus the Eigen vectors corresponding to the Eigen value 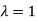 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 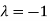 is
is
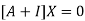
Where X is the column matrix of order 3 i.e.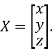
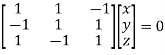
or 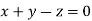
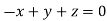
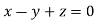
On solving we get 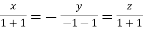 or
or 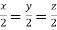 .
.
Thus the Eigen vectors corresponding to the Eigen value 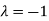 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Example-4:
Determine the Eigen values of Eigen vector of the matrix.
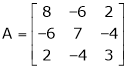
Solution:
Consider the characteristic equation as, 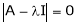
i.e. 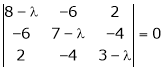
i.e. 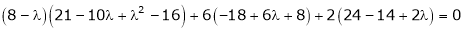
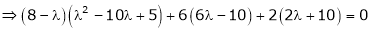
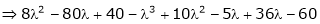
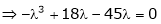
i.e. 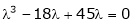
Which is the required characteristic equation.
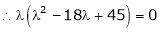
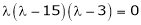
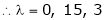 are the required Eigen values.
are the required Eigen values.
Now consider the equation
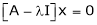 … (1)
… (1)
Case I:
If 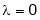 Equation (1) becomes
Equation (1) becomes
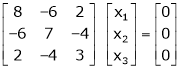
R1 + R2
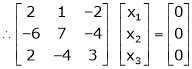
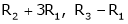
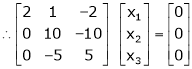
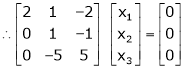
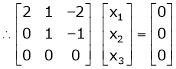
Thus 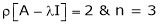
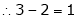 independent variable.
independent variable.
Now rewrite equation as,
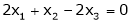
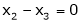
Put x3 = t
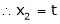 &
&
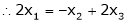
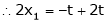
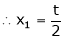
Thus 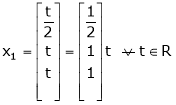 .
.
Is the eigen vector corresponding to 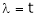 .
.
Case II:
If 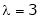 equation (1) becomes,
equation (1) becomes,
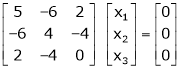
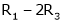
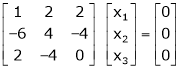
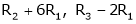
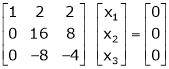
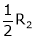
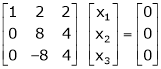
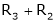
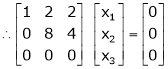
Here 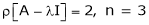
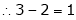 Independent variables
Independent variables
Now rewrite the equations as,
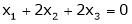
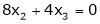
Put 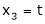
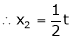 &
&
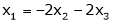
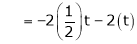
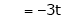
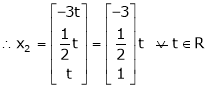 .
.
Is the eigen vector corresponding to 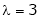 .
.
Case III:
If 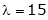 equation (1) becomes,
equation (1) becomes,
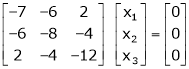
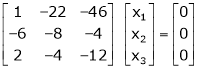
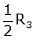
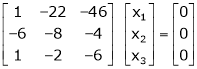
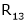
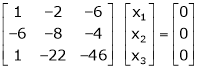
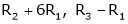
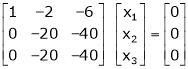
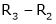
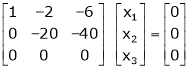
Here rank of 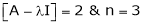
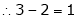 independent variable.
independent variable.
Now rewrite the equations as,
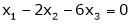
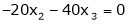
Put 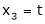
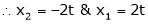
Thus 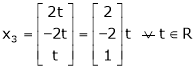 .
.
Is the eigen vector for 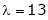 .
.
Example-5:
Find the Eigen values of Eigen vector for the matrix.
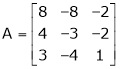
Solution:
Consider the characteristic equation as 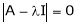
i.e. 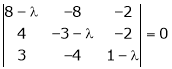
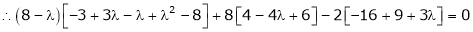
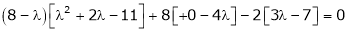
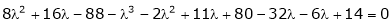
i.e. 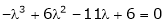
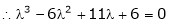
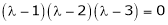
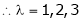 are the required eigen values.
are the required eigen values.
Now consider the equation
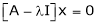 … (1)
… (1)
Case I:
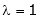 Equation (1) becomes,
Equation (1) becomes,
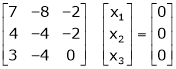
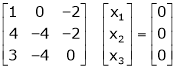
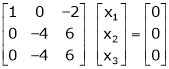
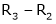
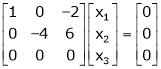
Thus 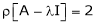 and n = 3
and n = 3
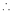 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
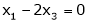
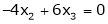
Put 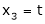
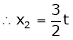 ,
, 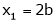
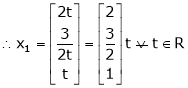
I.e.
the Eigen vector for 
Case II:
If 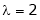 equation (1) becomes,
equation (1) becomes,
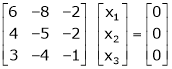
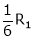
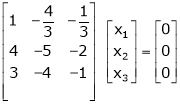
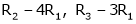
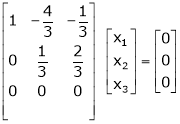
Thus 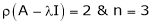
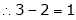
Independent variables.
Now rewrite the equations as,
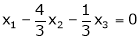
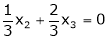
Put 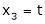
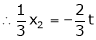
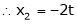
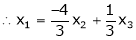
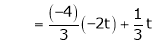
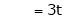
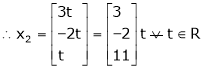
Is the Eigen vector for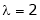
Now
Case III:-
If 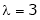 equation (1) gives,
equation (1) gives,
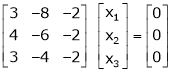
R1 – R2
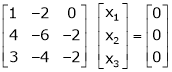
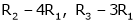
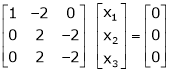
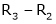
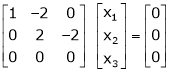
Thus 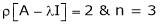
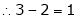
Independent variables
Now 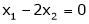
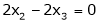
Put 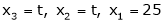
Thus
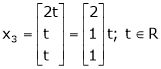
Is the Eigen vector for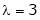
Key takeaways-
4. Let A he a square matrix, 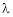 be any scalar then
be any scalar then 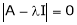 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A.
5. If two are more Eigen values are identical then the corresponding Eigen vectors may or may not be linearly independent.
6. The Eigen vectors corresponding to distinct Eigen values of a real symmetric matrix are orthogonal
Symmetric matrix:
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So, if aᵢⱼ denotes the entry in the i-th row and j-th column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero.
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 &
& 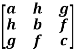
Example: check whether the following matrix A is symmetric or not?
A = 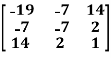
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
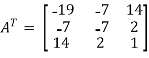
Here,
A = 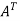
So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix
Then,
A = 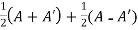
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Example: Let us test whether the given matrices are symmetric or not i.e., we check for,
A = 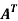
(1) A = 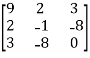
Now
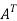 =
=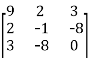
 A =
A = 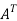
Hence the given matric symmetric
Example: let A be a real symmetric matrix whose diagonal entries are all positive real numbers.
Is this true for all of the diagonal entries of the inverse matrix A-1 are also positive? If so, prove it. Otherwise give a counter example
Solution: The statement is false, hence we give a counter example
Let us consider the following 2 2 matrix
2 matrix
A = 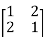
The matrix A satisfies the required conditions, that is A is symmetric and its diagonal entries are positive.
The determinant det(A) = (1)(1)-(2)(2) = -3 and the inverse of A is given by
A-1= 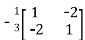 =
= 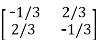
By the formula for the inverse matrix for 2 2 matrices.
2 matrices.
This shows that the diagonal entries of the inverse matric A-1 are negative.
Skew-symmetric:
A skew-symmetric matrix is a square matrix that is equal to the negative of its own transpose. Anti-symmetric matrices are commonly called as skew-symmetric matrices.
In other words-
Skew-symmetric matrix-
A square matrix A is said to be skew symmetrix matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2. All the main diagonal elements will always be zero.
For example-
A = 
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Example: Let A and B be n n skew-matrices. Namely AT = -A and BT = -B
n skew-matrices. Namely AT = -A and BT = -B
(a) Prove that A+B is skew-symmetric.
(b) Prove that cA is skew-symmetric for any scalar c.
(c) Let P be an m n matrix. Prove that PTAP is skew-symmetric.
n matrix. Prove that PTAP is skew-symmetric.
Solution: (a) (A+B)T = AT + BT = (-A) +(-B) = -(A+B)
Hence A+B is skew symmetric.
(b) (cA)T = c.AT =c(-A) = -cA
Thus, cA is skew-symmetric.
(c)Let P be an m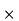 n matrix. Prove that PT AP is skew-symmetric.
n matrix. Prove that PT AP is skew-symmetric.
Using the properties, we get,
(PT AP)T = PTAT(PT)T = PTATp
= PT (-A) P = - (PT AP)
Thus (PT AP) is skew-symmetric.
Key takeaways-
Orthogonal matrix:
An orthogonal matrix is the real specialization of a unitary matrix, and thus always a normal matrix. Although we consider only real matrices here, the definition can be used for matrices with entries from any field.
Suppose A is a square matrix with real elements and of n x n order and AT is the transpose of A. Then according to the definition, if, AT = A-1 is satisfied, then,
A AT = I
Where ‘I’ is the identity matrix, A-1 is the inverse of matrix A, and ‘n’ denotes the number of rows and columns.
“Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix”
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Example: 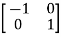 and
and  are the form of orthogonal matrices.
are the form of orthogonal matrices.
Example: prove Q= 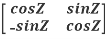 is an orthogonal matrix
is an orthogonal matrix
Solution: Given Q = 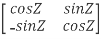
So,
QT = 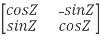 …..(1)
…..(1)
Now, we have to prove QT = Q-1
Now we find Q-1
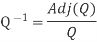
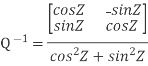
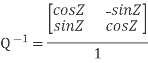
Q-1 = 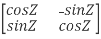 … (2)
… (2)
Now, compare (1) and (2) we get QT = Q-1
Therefore, Q is an orthogonal matrix.
Key takeaways-
Hermitian matrix:
A square matrix A = 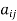 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
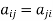
For example:
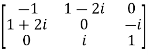
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 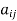 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
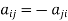
Note- All the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
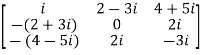
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew–Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 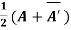 is hermitian and
is hermitian and 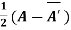 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 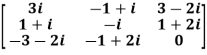
Let
A =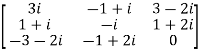
Therefore
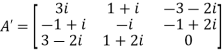
And
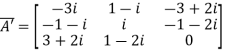
Let 
Again
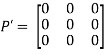
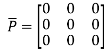
Hence P is a hermitian matrix.
Let 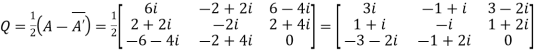
Again
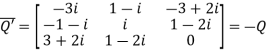
Hence Q is a skew- hermitian matrix.
We Check
P +Q=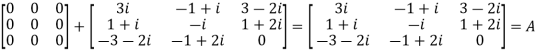
Hence proved.
Example2: If A = 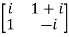 then show that
then show that
(i) 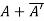 is hermitian matrix.
is hermitian matrix.
(ii) 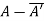 is skew-hermitian matrix.
is skew-hermitian matrix.
Given
A = 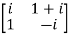
Then
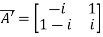
Let
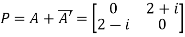
Also
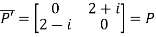
Hence P is a Hermitian matrix.
Let
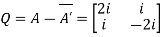
Also
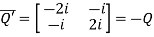
Hence Q is a skew-hermitian matrix.
Key takeaways-
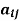
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’ . A = I
For example:
A =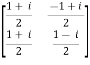 and its ( ͞A)’ =
and its ( ͞A)’ = 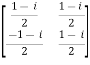
Then (͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
Two square matrix 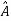 and A of same order n are said to be similar if and only if
and A of same order n are said to be similar if and only if
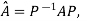 for some non singular matrix P.
for some non singular matrix P.
Such transformation of the matrix A into 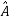 with the help of non singular matrix P is known as similarity transformation.
with the help of non singular matrix P is known as similarity transformation.
Similar matrices have the same Eigen values.
If X is an Eigen vector of matrix A then 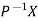 is Eigen vector of the matrix
is Eigen vector of the matrix 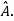
Reduction to Diagonal Form:
Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that
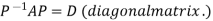
Where P is called the modal matrix and D is known as spectral matrix.
Procedure: let A be a square matrix of order 3.
Let three Eigen vectors of A are 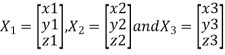 Corresponding to Eigen values
Corresponding to Eigen values 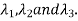
Let
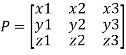
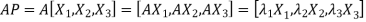 {by characteristics equation of A}
{by characteristics equation of A}
Or 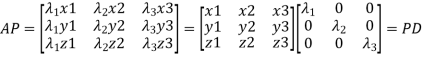
Or 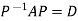
Note: The method of diagonalization is helpful in calculating power of a matrix.
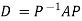 .Then for an integer n we have
.Then for an integer n we have 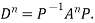
We are using the example of 1.6*
Example1: Diagonalise the matrix 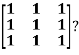
Let
A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 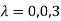 .
.
Then
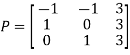
And
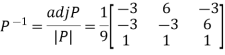
Also we know that 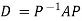
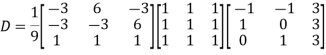
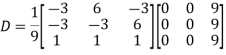
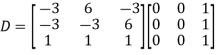
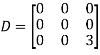
Example2: Diagonalise the matrix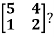
Let A =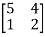
The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values 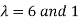 .
.
Then 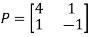 and also
and also 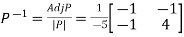
Also we know that 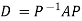
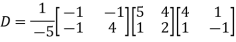
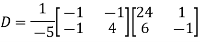
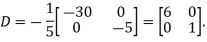
Key takeaways-
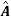
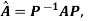 for some non singular matrix P.
for some non singular matrix P.
2. If X is an Eigen vector of matrix A then 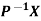 is Eigen vector of the matrix
is Eigen vector of the matrix 
References