Module-1
Matrix Algebra
Matrices: It is a rectangular arrangement of numbers formed by keeping them in m numbers of rows and n numbers of columns.
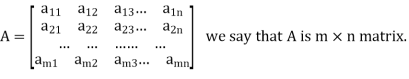
Algebra on Matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example: 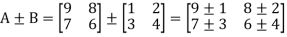
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 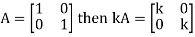
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example: 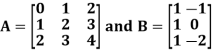
Then 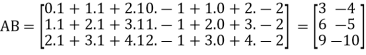
4. Power of Matrices: If A is A square matrix then
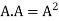
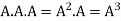 and so on.
and so on.
If 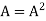 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 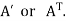
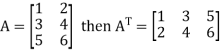
The transpose of matrix 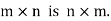 Also
Also 
Note: 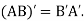
Example: If 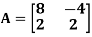 then prove that
then prove that 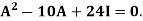
Sol.
Here,
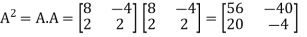
Then-
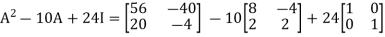
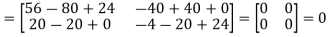
Example: If 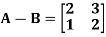 and
and 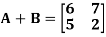 then find AB.
then find AB.
Sol.
Here we have-
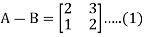
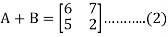
Now adding (1) and (2)-
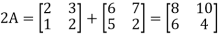
So that-
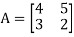
Then put the value of A in (2)-
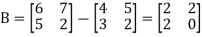
So that-
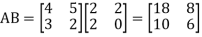
Types of matrices-
Row matrix:
A matrix with only one single row and many columns can be possible.
A = 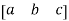
Column matrix:
A matrix with only one single column and many rows can be possible.
A = 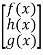
Square matrix:
A matrix in which number of rows is equal to number of columns is called a square matrix. Thus an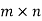 matrix is square matrix then m=n and is said to be of order n.
matrix is square matrix then m=n and is said to be of order n.
The determinant having the same elements as the square matrix A is called the determinant of the matrix A. denoted by |A|.
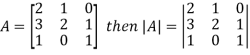
The diagonal elements of matrix A are 2, 2 and 1 is the leading and the principal diagonal.
The sum of the diagonal elements of square matrix A is called the trace of A.
A square matrix is said to be singular if its determinant is zero otherwise non-singular.
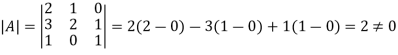
Hence the square matrix A is non-singular.
Diagonal matrix:
A square matrix is said to be diagonal matrix if all its non diagonal elements are zero.
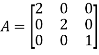
Scalar matrix:
A diagonal matrix is said to be scalar matrix if its diagonal elements are equal.
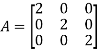
Identity matrix:
A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix or Unit matrix.
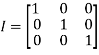
Null Matrix:
If all the elements of a matrix are zero, it is called a null or zero matrixes.
Ex:  etc.
etc.
Symmetric matrix:
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 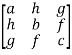
Example: check whether the following matrix A is symmetric or not?
A = 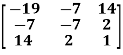
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
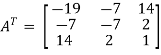
Here,
A = 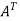
So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix .
Then,
A = 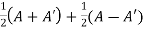
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Key takeaways-
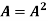
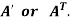
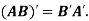
There are two types of linear equations-
1. Consistent
2. Inconsistent
Let’s understand about these two types of linear equations.
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Whereas,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) Consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) Inconsistent equations-
If Rank of A ≠ Rank of C
Matrix form of the linear system can be written as follows,
Ax = b
Where,
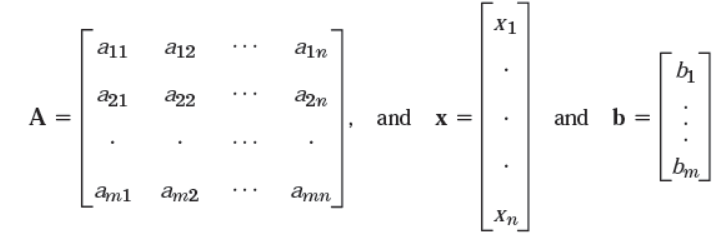
A is called augmented matrix.
Gauss elimination method can be presented as ,
Suppose there is a linear system in triangular form ,
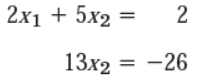
We can solve this as X2 = -26/13 = -2 and X1 = 6
Lets another set of eq. is given as ,
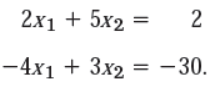
Its augmented matrix is given by,
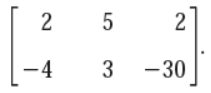
We eliminate X1 from the second eq.
To get the triangular system .we add twice the first equation to the second and we do same operation on rows of the augmented matrix. This gives,
-4X1 +4X1 +3X2 + 10X2 = -30 + 2.2
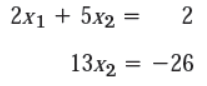
this is called Gauss elimination.
Example: find the solution of the following linear equations.
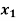 +
+ 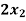 -
- 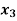 = 1
= 1
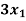 -
- 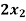 +
+ 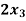 = 2
= 2
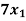 - 2
- 2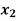 +
+ 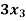 = 5
= 5
Sol. These equations can be converted into the form of matrix as below-
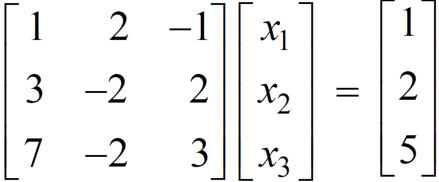
Apply the operation, 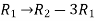 and
and 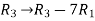 , we get
, we get
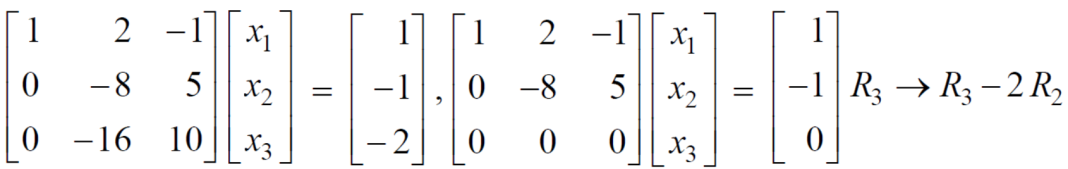
We get the following set of equations from the above matrix,
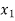 +
+ 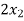 -
- 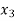 = 1 …………………..(1)
= 1 …………………..(1)
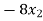 + 5
+ 5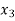 = -1 …………………(2)
= -1 …………………(2)
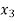 = k
= k
Put x = k in eq. (1)
We get,
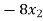 + 5k = -1
+ 5k = -1
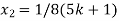
Put these values in eq. (1), we get
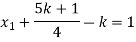
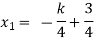
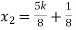 and
and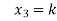
These equations have infinitely many solutions.
Key takeaways-
If Rank of A = Rank of C
2. Inconsistent equations-
If Rank of A ≠ Rank of C
Rank of a matrix by echelon form-
The rank of a matrix (r) can be defined as –
1. It has at least one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 
Sol. First we will convert the matrix M into echelon form,
M = 
Apply, 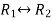 , we get
, we get
M = 
Apply 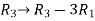 , we get
, we get
M = 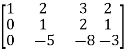
Apply 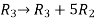
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 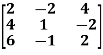
Sol. Convert the matrix A into echelon form,
A = 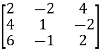
Apply 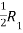
A = 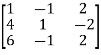
Apply 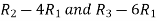 , we get
, we get
A = 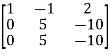
Apply 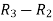 , we get
, we get
A = 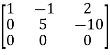
Apply 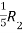 ,
,
A = 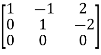
Apply 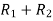 ,
,
A = 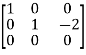
Therefore the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form.
A = 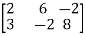
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 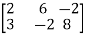
Apply, 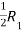
A = 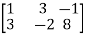
Apply 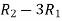 ,
,
A = 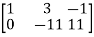
Apply 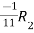
A = 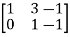
Apply 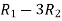
A = 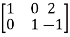
Hence the rank of the matrix will be 2.
Example: Find the rank of the following matrices by echelon form?
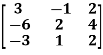
Let A = 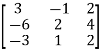
Applying 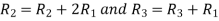
A 
Applying 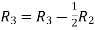
A 
Applying 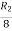
A 
Applying 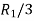
A 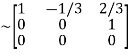
It is clear that minor of order 3 vanishes but minor of order 2 exists as 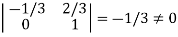
Hence rank of a given matrix A is 2 denoted by 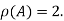
2. 
let A = 
Applying 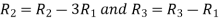

Applying 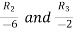
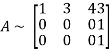
Applying 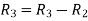
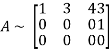
The minor of order 3 vanishes but minor of order 2 non zero as 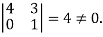
Hence the rank of matrix A is 2 denoted by 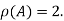
3. 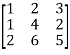
Let A = 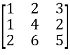
Apply 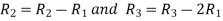

Apply 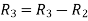

Apply 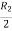
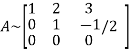
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 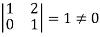
Hence the rank of given matrix is 2 i.e. 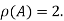
Inverse of a matrix by using elementary transformation (Gauss-Jordan method)
The following transformation are defined as elementary transformations-
1. Interchange of any two rows (column)
2. Multiplication of any row or column by any non-zero scalar quantity k.
3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.
The symbol ~ is used for equivalence.
Elementary matrices-
If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation-
Working steps-
1. Write A = IA
2. Perform elementary row transformation of A of the left side and I on right side.
3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to 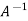
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
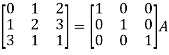
Apply 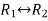 , we get
, we get
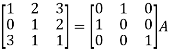
Apply 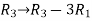
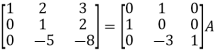
Apply 
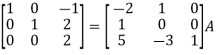
Apply 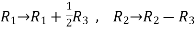
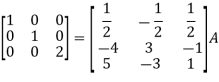
Apply 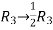
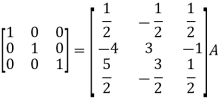
So that,
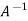 =
= 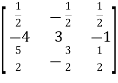
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
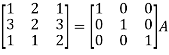
Apply 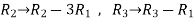
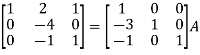
Apply 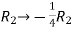
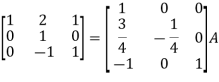
Apply 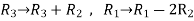
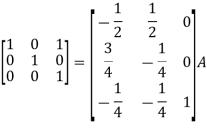
Apply 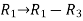
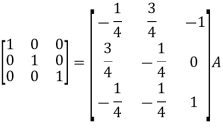
So that
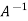 =
= 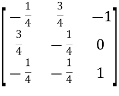
Example-3: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol.
Write the matrix ‘A’ as-
A = IA
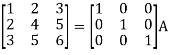
Apply 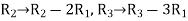
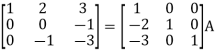
Apply 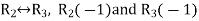
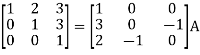
Apply 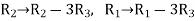
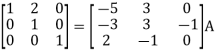
Apply 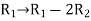
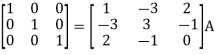
Then-
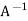 =
=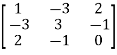
Vector-
An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.
If A be an mxn matrix then each row will be an n – vector & each column will be an m – vector.
Linear dependence-
A set of n – vectors. x1, x2, …….., xr is said to be linearly dependent if there exist scalars. k1, k2, …….,kr not all zero such that
k1 + x2k2 + …………….. + xrkr = 0 … (1)
Linear independence-
A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xrkr = 0
Important notes-
k1 = k2 = …….=kr = 0. Then the vector x1, x2, ……,xr are said to linearly independent.
Linear combination-
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xrkr
where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Results:
Example-1: Are the vectors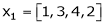 ,
,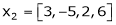 ,
,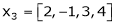 linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
Solution:
Consider a vector equation,
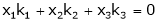
i.e. 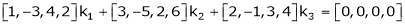
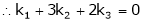
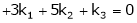
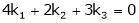
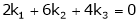
Which can be written in matrix form as,
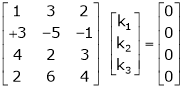
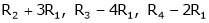
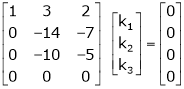
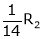
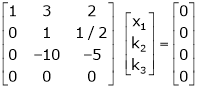
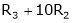
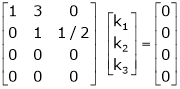
Here 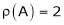 & no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
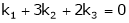
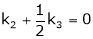
Put 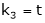
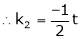 and
and
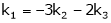
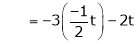
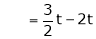
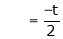
Thus 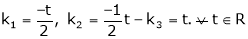
i.e. 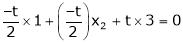
i.e. 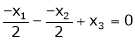
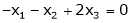
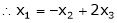
Since F11k2, k3 not all zero. Hence 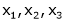 are linearly dependent.
are linearly dependent.
Example-2: Examine whether the following vectors are linearly independent or not.
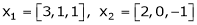 and
and 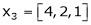 .
.
Solution:
Consider the vector equation,
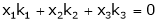
i.e. 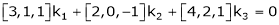 … (1)
… (1)
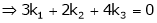
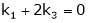
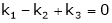
Which can be written in matrix form as,
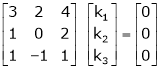
R12
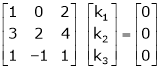
R2 – 3R1, R3 – R1
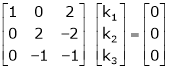
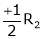
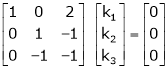
R3 + R2
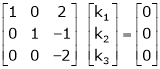
Here Rank of coefficient matrix is equal to the no. of unknowns. i.e. r = n = 3.
Hence the system has unique trivial solution.
i.e. 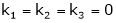
i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.
Example-3: At what value of P the following vectors are linearly independent.
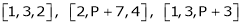
Solution:
Consider the vector equation.
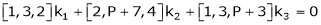
i.e.
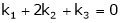
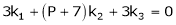
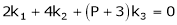
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
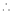 consider
consider 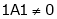 .
.
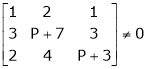 .
.
i.e.
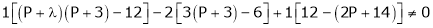
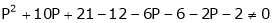
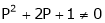
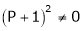
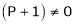
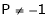
Thus for 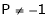 the system has only trivial solution and Hence the vectors are linearly independent.
the system has only trivial solution and Hence the vectors are linearly independent.
Note:-
If the rank of the coefficient matrix is r, it contains r linearly independent variables & the remaining vectors (if any) can be expressed as linear combination of these vectors.
Key takeaways-
x = x1 k1 + x2 k2 + ……….+xrkr
where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
3. A set of two or more vectors are said to be linearly dependent if at least one vector can be written as a linear combination of the other vectors.
References