Module – 2
Differential Equation
An exact differential equation is formed by differentiating its primitive solution without any other process mdx + Ndy =0 is said to be an exact differential equation if it is satisfies the following conditions
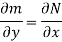
Method for solving exact differential equation
Step I :-Integrate m with respect to x keeping by constant
Step II :-Integrate with respect to y only those terms of N which do not contain x.
Step III :-Result of step I + Result of step II= constant
Solve. 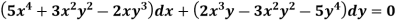
Ans.Here m=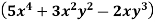
N=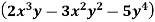
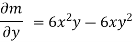
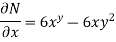
Since, 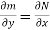 the given equation is exact.
the given equation is exact.
Now, (Term of N is not containing x)dy=c
(Term of N is not containing x)dy=c
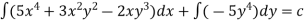
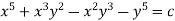
An exact differential equation is formed by differentiating its primitive solution without any other process mdx + Ndy =0 is said to be an exact differential equation if it is satisfies the following conditions

Method for solving exact differential equation
Step I :-Integrate m with respect to x keeping by constant
Step II :-Integrate with respect to y only those terms of N which do not contain x.
Step III :-Result of step I + Result of step II= constant
Solve. 
Ans.Here m=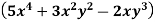
N=
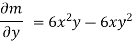
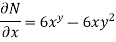
Since, 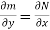 the given equation is exact.
the given equation is exact.
Now,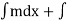 (Term of N is not containing x)dy=c
(Term of N is not containing x)dy=c

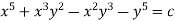
A differential equation of the form 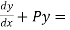 is called linear differential equation where p and q are function of x(but not of y) or constant
is called linear differential equation where p and q are function of x(but not of y) or constant
Note:-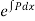 is called integrating factor
is called integrating factor

Working rule
Step 1:- Convert the given equation to the standard form of linear differential equation i.e.
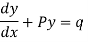
Step 2:- Find the integrating factor

Step 3:- then the solution is
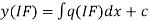
Example:- Solve (x+1)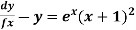
Ans.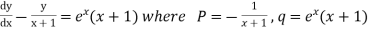
IF=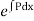
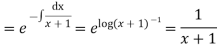
Then solution is
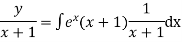
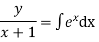
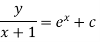
The equation of the form 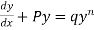 where p and q are constant or function of x can be reduced to the linear form on dividing by
where p and q are constant or function of x can be reduced to the linear form on dividing by 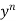 and substituting
and substituting 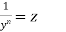
Example. Solve 
Ans. Given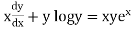
Dividing by xy we get

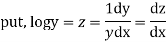
Equation (1) becomes

Where, 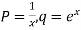
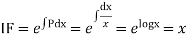
Its solution is

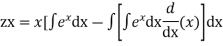
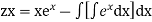
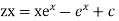
References
1. Ordinary and Partial Differential equations by J. Sihna Ray and S Padhy, Kalyani Publishers
2. Advance Engineering Mathematics by P.V.O’NEIL, CENGAGE
3. Ordinary Differential Equation by P C Biswal , PHI secondedition.
4. Engineering Mathematics by P. S. Das & C. Vijayakumari, Pearson. N.B:Thecourseisof3creditwith4contacthours.