UNIT-1

Basic Probability

1.1. Probability spaces, Conditional probability, Independence

Probability is the study of chances. Probability is the measurement of the degree of uncertainty and therefore, of certainty of the occurrence of events.

A probability space is a three-tuple (S, F, P) in which the three components are

1. Sample space: A nonempty set S called the sample space, which represents           all possible outcomes.
2. Event space: A collection F of subsets of S, called the event space.
3. Probability function: A function P : FR, that assigns probabilities to the events in F.

Basic definitions-

1. Exhaustive events- The set of all possible outcomes of an experiment is called exhaustive event of sample space.

Example-

1. If we toss a coin then the sample space is

S = {H, T}, where H and T denote head and tail respectively and n(S) = 2

2. If a coin is tossed thrice or three coins are tossed simultaneously, then the sample space is

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and n(S) = 8.

3. If a coin is tossed 4 times or four coins are tossed simultaneously then the sample space is

S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THHT,

THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT} and n(S) = 16.

Each outcome is called sample point.

Example- If a die is thrown twice, then getting (1, 1) or (1, 2) or (1, 3) or…or (6, 6) is a sample point.

2. Mutually exclusive events- When the occurrence of one event excludes the occurrence of the other then these two events said to be mutually exclusive

3. Equally likely- Two events are said to be equally likely if one of them cannot be occur in preference to the others.

Random experiment-

An experiment in which all the possible outcomes are known in advance but we cannot predict as to which of them will occur when we perform the experiment.

Example-‘Throwing a die’ and ‘Drawing a card from a well shuffled pack of 52 playing cards ‘are the examples of random experiment

Event-

Set of one or more possible outcomes of an experiment constitutes what is known as event. Thus, an event can be defined as a subset of the sample space

Favourable cases-

The cases which favour to the happening of an event are called favourable cases

Example-For the event of getting an even number in throwing a die, the number of favourable cases is 3 and the event in this case is {2, 4, 6}.

Odds in favour of an event and odds against an event-

If the number of favourable cases are ‘m’ and the number or not favourable cases are ‘n’.

Then-

1. Odds in favour of the event = m/n

2. Odds against the event = n/m

Classical definition of probability-

Suppose there are ‘n’ exhaustive cases in a random experiment which is equally likely and mutually exclusive.

Let ‘m’ cases are favourable for the happening of an event A, then the probability of happening event A can be defined as-

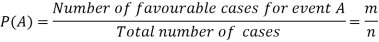
Probability of non-happening of the event A is defined as-

Note- Always remember that the probability of any events lies between 0 and 1.

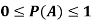
Expected value-

Let are the probabilities of events and respectively. Then the expected value can be defined as-

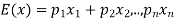
Example: Bags contains 7 red and 8 black balls then find the probability of getting a red ball.

Solution:

Here total cases = 7 + 8 = 15

According to the definition of probability,

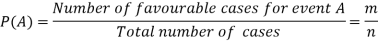
So that, here favourable cases-  red balls = 7

Then,

Addition and multiplication law of probability-

Addition law-

If 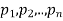are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by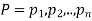

Note-

If two events A and B are not mutually exclusive then then probability of the event that either A or B or both will happen is given by-

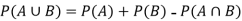
Example: A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white.

Solution:

Here we have two mutually exclusive cases-

1. The first bag is chosen

2. The second bag is chosen

The chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.

So that the probability of drawing a white ball from first bag is-

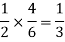
And the probability of drawing a white ball from second bag is-

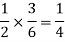
Here the events are mutually exclusive, then the required probability is-

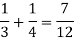
Example: 25 lottery tickets are marked with first 25 numerals. A ticket is drawn at random.

Find the probability that it is a multiple of 5 or 7.

Solution:

Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.

So that

A = {5, 10, 15, 20, 25}

B = {7, 14, 21}

Here, as A B = ,

A and B are mutually exclusive

Then,

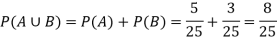
Multiplication law-

For two events A and B-

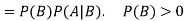
Here 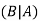is called conditional probability of B given that A has already happened.

Now-

If A and B are two independent events, then-

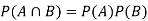
Because in case of independent events-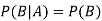 

Example: A bag contains 9 balls, two of which are red three blue and four black.

Three balls are drawn randomly. What is the probability that-

1. The three balls are of different colours

2. The three balls are of the same colours.

Solution:

1. Three balls will be of different colour if one ball is red, one blue and one black ball are drawn-

Then the probability will be-

2. Three balls will be of same colour if one ball is red, one blue and one black ball are drawn-

Then the probability will be-

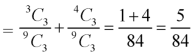
Example: A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?

Solution:

The sample space is-   S = {1, 2, 3, 4, 5, 6}

Let A be the event that the outcome is a number which is greater than three and  B be the event that it is a prime.

So that-

A = {4, 5, 6} and B = {2, 3, 5} and hence

P(A) = 3/6, P(B) = 3/6 and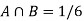

Now the required probability-

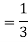
Example: Two cards are drawn from a pack of playing cards in succession with replacement of first card. Find the probability that the both are the cards of heart.

Solution:

Let A be the event that first card drawn is a heart and B be the event that second card is a heart card.

As the cards are drawn with replacement,

Here A and B are independent and the required probability will be-

Example: Two male and female candidates appear in an interview for two positions in the same post. The probability that the male candidate is selected is 1/7 and the female candidate selected is 1/5.

What is the probability that-

1. Both of them will be selected

2. Only one of them will be selected

3. None of them will be selected.

Solution:

Here, P (male’s selection) = 1/7

And

P (female’s selection) = 1/5

Then-

1.

2.

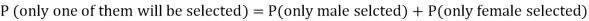
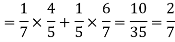
3.

Example: A can hit a target 3 times in 5 shots, B 2 times in 5 shots and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.

What is the probability that-

1. Two shots hit

2. At least two shots hit

Solution:

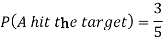
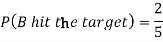
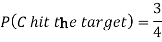
1. Now probability that 2 shots hit the target-

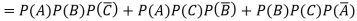
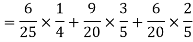
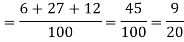
2.

Probability of at least two shots hitting the target

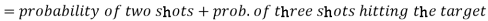
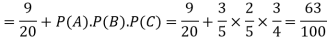
Conditional Probability-

Suppose A and B are two events of a sample space S and P(B) is non-zero, then conditional probability of the event A, given B,

It is given by P(A/B) and read as Probability of A given B-

Defined by-

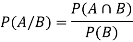
Note- If two events A and B are independent then-

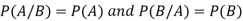
Multiplication theorem for conditional probability-

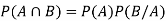
Example: A bag contains 12 pens of which 4 are defective. Three pens are picked at random from the bag one after the other.

Then find the probability that all three are non-defective.

Solution:

Here the probability of the first which will be non-defective = 8/12

By the multiplication theorem of probability,

If we draw pens one after the other then the required probability will be-

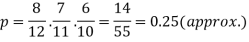
Example: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.

Solution:

Here it is given that-

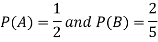
Now we have to find-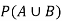
 

Both two events are independent. So that-

1.2. Discrete random variables & Independent random variables

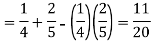
A random variable is said to be discrete if it has either a finite or a countable number of values

The number of students present each day in a class during an academic session is an example of discrete random variable as the number cannot take a fractional value.

Probability mass function-

Let X be a r.v. Which takes the values 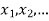and let P[X = 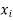] = p(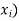. This function p(xi), i =1,2, … defined for the values 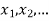assumed by X is called probability mass function of X satisfying p(xi) ≥0 and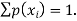

Example: A random variable x has the following probability distribution-

Then find-

1. Value of c.

2. P[X≤3]

3. P[1 < X <4]

Solution:

We know that for the given probability distribution-

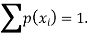
So that-

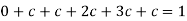
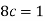
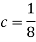
2.

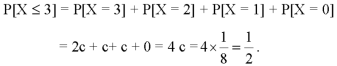
3.

Independent random variables-

Two discrete random variables X and Y are said to be independent only if-

Note- Two events are independent only if

Example: Two discrete random variables X and Y have-

And

P[X = 1, Y = 1] = 5/9.

Check whether X and Y are independent or not?

Solution:

First we write the given distribution In tabular form-

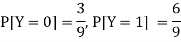
Now-

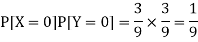
But

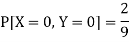
So that-

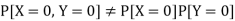
Hence X and Y are not independent.

1.3. The multinomial distribution

Multinomial experiments consists of the following properties-

1. The trials are independent.

2. Each trial has discrete number of possible outcomes.

3. The Experiments consists of n repeated trials.

Note- Binomial distribution is a special case of multinomial distribution.

Multinomial distribution-

A multinomial distribution is the probability distribution of the outcomes from a multinomial experiment.

The multinomial formula defines the probability of any outcome from a multinomial experiment.

Multinomial formula-

Suppose there are n trials in a multinomial experiment and each trial can result in any of k possible outcomes 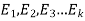. Now suppose each outcome can occur with probabilities .

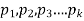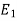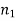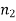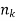Then the probability occurs times, occurs times and occurs times

Is-

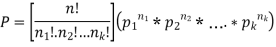
Example: If we have 10 balls in a bag, in which 2 are red, 3 are green and remaining are blue colour balls. Then we select 4 balls randomly form the bag with replacement, then what will be the probability of selecting 2 green balls and 2 blue balls.

Solution:

Here this experiment has 4 trials so n = 4.

The required probability will be-

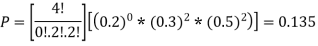
So that-

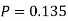
Example:You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?

Solution:

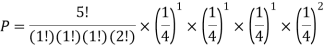
Example: A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf

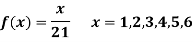
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.

Solution:

1.4. Poisson approximation to the binomial distribution

When n is large and p is very small then the Poisson distribution can be used to approximate the binomial distribution.

We know that the distribution function of binomial distribution is given as-

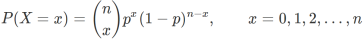
The Binomial distribution can be approach define by Poisson when n is big and p is small with np < 10, as specified above. This is correctsince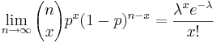, where λ = np.

Example: A plant places biscuits into boxes of 100. The probability that a biscuit is cracked is 0.03. Find the probability that a box contains 2 cracked biscuits

Solution:

This is a binomial distribution by means of n = 100 besides p = 0.03.

These standards are external the range of the counters and include lengthy calculations.

Using the Poisson estimate (test: np = 100 x 0.3 = 3, which is less than 5)

Let X be the random variable of the number of cracked biscuits

The mean λ = np = 100 × 0.3 = 3

P(X = 2) = 0.224 (from counters)

The probability that a box contains two broken biscuits is 0.224.

1.5. Infinite sequence of Bernoulli trials

Let a product is tested which may be defective or non-defective, let p be the probability of non-defective and q = 1-p be the probability of defective product.

And let X be a random variable which takes 1 if success occurs and 0 if failure occurs.

Therefore-

P[X = 1] = p

P[X = 0] = q = 1- p

This experiment is known as a Bernoulli trial and the random variable X is a Bernoulli variable.

Conditions for Bernoulli tests

1. A finite number of tests.

2. Each trial must have exactly two results: success or failure.

3. The tests must be independent.

4. The probability of success or failure must be the same in each test.

Bernoulli distribution-

A discrete random variable said to be follow a Bernoulli distribution with parameter p if its p.m.f is given by-

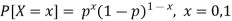
Bernoulli distribution in tabular form can be given as-

1. Mean of the Bernoulli distribution is p.

2. Variance = p(1-p)

Example: If X be a random variable following a Bernoulli distribution with parameter p = 0.6, then find its mean and variance.

Solution:

Mean = p = 0.6

Variance = p(1-p) = 0.6 (1 – 0.6) = 0.6 ×0.4 = 0.24

Example: If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?

Solution:

Probability that the bulb is defective, p = 0.8

Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2

Example: 10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.

Solution:

Probability of obtaining the head, p = 0.6

Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4

Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736

Example: In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
 

Solution:

Probability of obtaining a correct answer, p = 1414 = 0.25

Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75

Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044

1.6. Sums of independent random variables

We discussed earlier how to derive the distribution of the sum of two independent random variables. How do we obtain the distribution of the sum of more than two mutually independent random variables? Suppose, ..., they are mutually independent random variables and leave their sum: the distribution of can be derived recursively, using the results for sums of two previous random variables:

1. First, define and calculate the distribution of;

2. Then define and calculate the distribution of;

3. And so on, until the distribution of

Exercise-

Let X be a discrete random variable with support mass function and probability and another discrete random variable, independent of, with support mass function and probability.

Derive the probability mass function from the sum

Solution

The support of is the probability mass function of, evaluated in is evaluated in, is evaluated in, is evaluated in, therefore, the probability mass function is

1.7. Expectations of discrete random variables

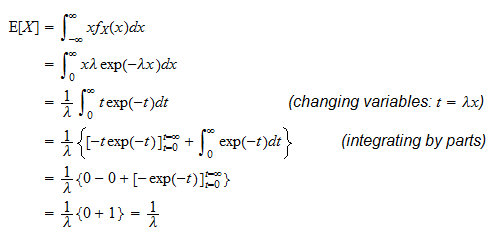
Let a random variable X has a probability distribution which assumes the values say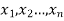 with their associated probabilities then the mathematical expectation can be defined as-

The expected value of a random variable X is written as E(X).

Expected value for a continuous random variable is

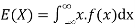
Example: If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.

Solution:

We know that-

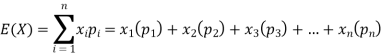
So that-

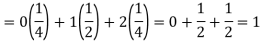
Example: Find the expectations of the number of an unbiased die when thrown.

Solution:

Let X be a random variable which represents the number on a die when thrown.

X can take the values-

1, 2, 3, 4, 5, 6

With

P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6

The distribution table will be-

Hence the expectation of number on the die thrown is-

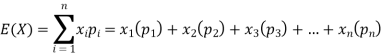
So that-

1.8. Moments, Variance of sum, Correlation coefficients

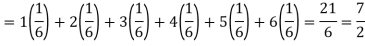
Moments-

The r’th moment of a variable x about the mean is denoted by and defined as-

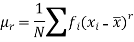
The r’th moment of a variable x about any point ‘a’ will be-

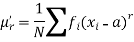
Relationship between moments about mean and moment about any point-

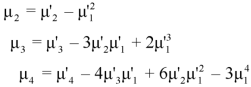
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.

Example- Height and weight of the persons of a group.

The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.

Variance of sum-

If two sets are independent then-

Var (x + y) = var (x) + var (y)

When the  data is not dependent then-

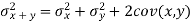
Karl Pearson’s coefficient of correlation-

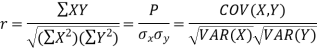
Here- 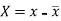and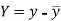

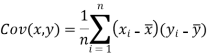
Note-

1. Correlation coefficient always lies between -1 and +1.

2. Correlation coefficient is independent of change of origin and scale.

3. If the two variables are independent then correlation coefficient between them is zero.

Example: Find the correlation coefficient between Age and weight of the following data-

Sol.

x	y					( ) )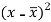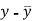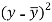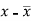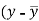
30	56	-10	100	-4	16	40
44	55	4	16	-5	25	-20
45	60	5	25	0	0	0
43	64	3	9	4	16	12
34	62	-6	36	2	4	-12
44	63	4	16	3	9	12
Sum= 240	360	0	202	0	70	32

Karl Pearson’s coefficient of correlation-

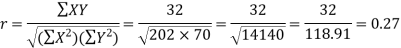
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.

Short-cut method to calculate correlation coefficient-

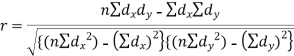
Here,

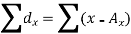
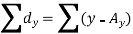
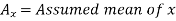
Example: Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-

Solution:

X	Y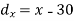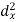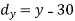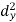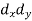
10	90	-20	400	20	400	-400
20	85	-10	100	15	225	-150
30	80	0	0	10	100	0
40	60	10	100	-10	100	-100
50	45	20	400	-25	625	-500
Sum = 150	360	0	1000	10	1450	-1150

Short-cut method to calculate correlation coefficient-

1.9. Chebyshev’s inequality

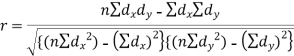
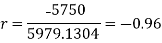
The Chebyshev inequality enables us to obtain bounds on probability when both the mean and variance of a random variable are known. The inequality can be stated as follows:

Let X be a random variable with mean μ and variance σ2. Then, for any b>0,

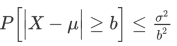
Proof:

Since (X−μ)2 is a nonnegative random variable, we can invoke the Markov inequality with a=b2, to obtain

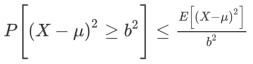
Since (X−μ)2≥b2 if and only if |X−μ|≥b, the preceding inequality is equivalent to

P[|X−μ|≥b]≤E[(]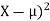

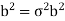
Example: A individual is selected from a population randomly who has average income of 40,000 dollars with SD 20,000 dollars, what will be the probability of selecting an individual whose income is either less than 10,000 dollars or greater than 70,000 dollars.

Solution:

Here we use Chebyshev inequality to solve such  problems.

If X denotes income then X is less than  10,000 dollars or greater than 70,000 dollars only if-

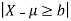
Where 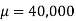and b = 30,000 the the probability-

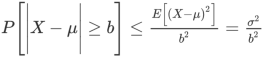
= 400,000,000/900,000,000 = 4/9

Exercise 1

Let  be a random variable such that

Find a lower bound to its variance.

Solution:

The lower bound can be derived thanks to Chebyshev's inequality: