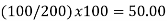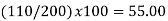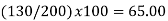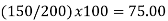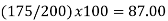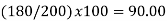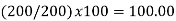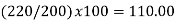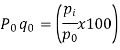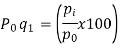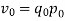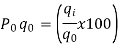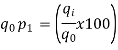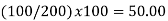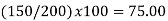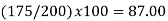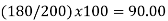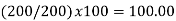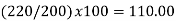Unit -VI
Index numbers
Index numbers are intended to measure the degree of economic changes over time. These numbers are values stated as a percentage of a single base figure. Index numbers are important in economic statistics. In simple terms, an index (or index number) is a number displaying the level of a variable relative to its level (set equal to 100) in a given base period | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
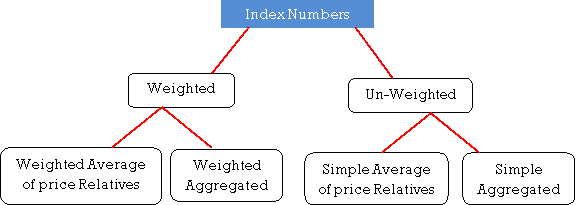
Types of Index Numbers | |||||||||||||||||||||||||||
Simple Index Number: A simple index number is a number that measures a relative change in a single variable with respect to a base. These type of Index numbers are constructed from a single item only. This ratio is then finally converted to a percentage 100 Value in Base Year Value in Period Index for any Period x i i = i.e. Simple Price Index for period i = 1,2,3 ... Will be 100 0 0 x p pP i i = …………(6-1) Similarly, Simple Quantity Index for period i = 1,2,3 ... Will be 100 0 0 x q qQ i i = …………(6-2)
Composite Index Number: A composite index number is a number that measures an average relative change in a group of relative variables with respect to a base. A composite index number is built from changes in a number of different items.
Price index Numbers: Price index numbers measure the relative changes in prices of a commodity between two periods. Prices can be either retail or wholesale. Price index number is useful to comprehend and interpret varying economic and business conditions over time.
Methods of constructing index numbers: There are two methods to construct index numbers: Price relative and aggregate methods (Srivastava, 1989)
| |||||||||||||||||||||||||||

In aggregate methods, the aggregate price of all items in a given year is expressed as a percentage of same in the base year, giving the index number. Weighted aggregative index numbers: These index numbers are the simple aggregative type with the fundamental difference that weights are assigned to the various items included in the index. | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Characteristics of index numbers:
6.2 Problems In The Construction Of Price Index Numbers
| |||||||||||||||||||||||||||
BASE SHIFTING. The need for shifting the base may arise either | |||||||||||||||||||||||||||
(i) when the base period of a given index number series is to be made more recent, or | |||||||||||||||||||||||||||
(ii) when two index number series with different base periods are to be compared, or | |||||||||||||||||||||||||||
(iii) When there is need for splicing two overlapping index number series. | |||||||||||||||||||||||||||
Whatever be the reason, the technique of shifting the base is simple: | |||||||||||||||||||||||||||
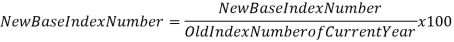 | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Example | |||||||||||||||||||||||||||
Reconstruct the following indices using 1997 as base:
| |||||||||||||||||||||||||||
Shifting the Base Period
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
SPLICING TWO OVERLAPPING INDEX NUMBER SERIES | |||||||||||||||||||||||||||
Splicing two index number series means reducing two overlapping index series with Different base periods into a single series either at the base period of the old series (one with an old base year), or at the base period of the new series (one with a recent Base year). This actually amounts to changing the weights of one series into the Weights of the other series.
| |||||||||||||||||||||||||||
Splicing the New Series to Make it Continuous with the Old Series | |||||||||||||||||||||||||||
Here we reduce the new series into the old series after the base year of the former. As Shown in Table 6.8.2(i), splicing here takes place at the base year (1980) of the new Series. To do this, a ratio of the index for 1980 in the old series (200) to the index of 1980 in the new series (100) is computed and the index for each of the following years in the new series is multiplied by this ratio | |||||||||||||||||||||||||||
Splicing the New Series with the Old Series
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Splicing the Old Series to Make it Continuous with the New Series | |||||||||||||||||||||||||||
This means reducing the old series into the new series before the base period of the Letter. As shown in Table , splicing here takes place at the base period of the New series. To do this, a ratio of the index of 1980 of the new series (100) to the index Of 1980 of the old series (200) is computed and the index for each of the preceding Years of the old series are then multiplied by this ratio.
| |||||||||||||||||||||||||||
Splicing the Old Series with the New Series
|
An alternative system of assigning weights lies in using value weights. The value weight 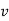 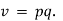 | ||||||||||||||||||
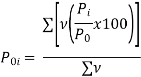 | …………….. (6-23) | |||||||||||||||||
Then 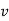 | ||||||||||||||||||
The product of the base period prices and the base period quantities denoted as 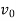 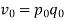 | ||||||||||||||||||
The product of the base period prices and the given period quantities denoted As  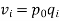 | ||||||||||||||||||
When 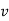  | ||||||||||||||||||
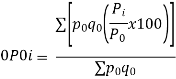 | …………….. (6-24) | |||||||||||||||||
It may be seen that  Similarly, When 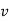 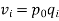 | ||||||||||||||||||
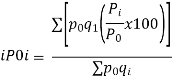 | ……….. (6-25) | |||||||||||||||||
| ||||||||||||||||||
It may be seen that  If the index of weighted average of quantity relatives is defined as | ||||||||||||||||||
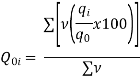 | …….. (6-26) | |||||||||||||||||
Then v can be obtained either as | ||||||||||||||||||
The product of the base period quantities and the base period prices denoted as  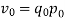 | ||||||||||||||||||
The product of the base period quantities and the given period prices denoted As 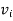 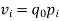 | ||||||||||||||||||
When 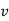 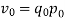 | ||||||||||||||||||
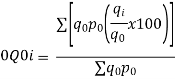 | …….. (6-27) | |||||||||||||||||
It may be seen that 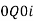 Similarly, When  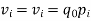 | ||||||||||||||||||
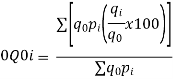 | …….. (6-28) | |||||||||||||||||
It may be seen that 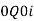 | ||||||||||||||||||
| ||||||||||||||||||
Example 6-5 | ||||||||||||||||||
From the data in Example 6.2 find the: | ||||||||||||||||||
Index of Weighted Average of Price Relatives, using (i) 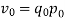 (ii) 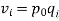 | ||||||||||||||||||
| ||||||||||||||||||
Index of Weighted Average of Quantity Relatives, using (i) 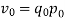 (ii) 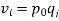
| ||||||||||||||||||
Calculations for Index of Weighted Average of Price Relatives (Base Year = 1980)
| ||||||||||||||||||
| ||||||||||||||||||
Index of Weighted Average of Price Relatives, using | ||||||||||||||||||
(i) 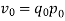 | ||||||||||||||||||
| 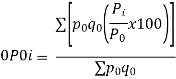 |
| ||||||||||||||||
| 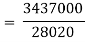 |
| ||||||||||||||||
| 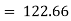 |
| ||||||||||||||||
| ||||||||||||||||||
(ii) 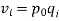 | ||||||||||||||||||
|  |
| ||||||||||||||||
| 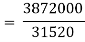 |
| ||||||||||||||||
| 
|
| ||||||||||||||||
Calculations for Index of Weighted Average of Quantity Relatives (Base Year = 1980)
| ||||||||||||||||||
| ||||||||||||||||||
Index of Weighted Average of Quantity Relatives, using | ||||||||||||||||||
(i) 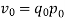 | ||||||||||||||||||
|  |
| ||||||||||||||||
| 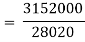 |
| ||||||||||||||||
|  |
| ||||||||||||||||
(ii) 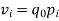 | ||||||||||||||||||
| 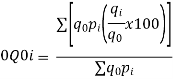 |
| ||||||||||||||||
| 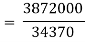 |
| ||||||||||||||||
| 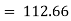 |
| ||||||||||||||||
| ||||||||||||||||||
Although the indices of weighted average of price/quantity relatives yield the same results as the Laspeyre's or Paasche's price/quantity indices, we do construct these indices also in situations when it is necessary and advantageous to do so. Some such situations are as follows: | ||||||||||||||||||
When a group of commodities is to be represented by a single commodity in the Group, the price relative of the latter is weighted by the group as a whole. | ||||||||||||||||||
Where the price/quantity relatives of individual commodities have been computed, These can be more conveniently utilised in constructing the index. | ||||||||||||||||||
Price/quantity relatives serve a useful purpose in splicing two index series having Different base periods. | ||||||||||||||||||
Depersonalizing a time series requires construction of a seasonal index, which also requires the use of relatives. | ||||||||||||||||||
BASE SHIFTING. The need for shifting the base may arise either | |||||||||||||||||||||||||||
(i) when the base period of a given index number series is to be made more recent, or | |||||||||||||||||||||||||||
(ii) when two index number series with different base periods are to be compared, or | |||||||||||||||||||||||||||
(iii) when there is need for splicing two overlapping index number series. | |||||||||||||||||||||||||||
Whatever be the reason, the technique of shifting the base is simple: | |||||||||||||||||||||||||||
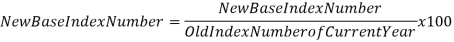 | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Example | |||||||||||||||||||||||||||
Reconstruct the following indices using 1997 as base:
| |||||||||||||||||||||||||||
Shifting the Base Period
|
Test of index number -
Unit Test:
This test states that the formula for constructing an index number should be independent of the units in which prices and quantities are expressed. All methods, except simple aggregative method, satisfy this test.
Time Reversal Test:
This test guides whether the method works both ways in time forward and backward. To quote Fisher, Time Reversal Test is the test which gives the same ratio between one point of comparison and the other, for calculation of index number, no matter which of the two is taken as base. In other words, when the index numbers of the two years are constructed by reversing the base year, they should be reciprocals of each other so that their product is unity.
Symbolically the test is represented as:
P01 X P10 = 1
Where P01 is the index for time “1” on time “0” as base and P10 is the index for time “0” on time “1” as base. If the product is not unity, the method suffers from time bias.
Time reversal test is satisfied by
- Simple aggregative method
- Fisher’s method
- Marshall-Edgeworth’s method and
- Kelly’s method.
Factor Reversal Test:
Fisher has described this test in the following words: Just as each formula should permit the interchange of the two items without giving inconsistent results, so it ought to permit interchanging the prices and quantities without giving inconsistent result, i.e., the two results multiplied together should give the true value ratio.”
In simple words, the test means that the change in the price multiplied by the change in the quantity should be equal to the total change in the value. The total value of a given commodity in a given year is the product of the quantity and the price per unit (total value = p x q) . The ratio of the total value in one year to the total value in the preceding
Year is p1q1 / p0q0. Symbolically the test is represented as
P01 x Q01 = Σp1q1 / Σp0q0 V01
Where P01 denotes price index and Q01 , quantity index number.
This test is satisfied by Fisher’s method only.
Circular Test:
According to this, if indices are constructed for year one based on year zero, for year two based on year one and for year zero based on year two, the product of all the indices should be equal to 1.
Symbolically
P01 X P12 X P20 = 1
This test is satisfied by
- Simple aggregative method and
- Kelly’s method.
Customer price Index
The Consumer Price Index (CPI) measures the average price change of a set of consumer goods and services. CPIs can be calculated for single items or a predetermined group of items. All of these items are defined as "household goods and services."
Some of the household goods and services that CPI might measure include:
- Food
- Transportation
- Health and medical care
- Clothing
- Energy
- Education
- Recreation
Typically, the CPI is used to measure inflation and determine the cost of living at a given time. It provides important insight for economists, governments and companies.
Uses of Customer price Index
The consumer price index is mainly used to measure inflation over a given period of time. It can also be leveraged to determine the cost of living.
CPI is mainly used to determine the efficacy of economic policies. Inflation indicates the health (or lack thereof) of an economy, so tracking it and responding to it appropriately is important for policymakers. When inflation sharply increases or decreases, the CPI provides economists and policymakers insight into how a government's economic policy affects the market.
This gives the ability to better understand whether current policies are working properly and how a government might be able to create better policies in the future.
The inflation rates and cost of living that CPI identifies can have a huge impact on the financial lives of consumers. In fact, when inflation is identified, the Federal Reserve will often take actions to stop an economy from overheating. This can ultimately result in loans becoming more expensive for borrowers.
CPI can also be used to shape government assistance policies. It will often help determine who is eligible for programs such as social security and other help. It also can result in wage adjustments to account for cost-of-living.
Reference-
- Https://www.thestreet.com/personal-finance/what-is-the-consumer-price-index-and-how-is-it-used-15066056
- Https://www.owlgen.in/what-are-the-various-tests-of-adequacy-of-index-number-formula/
- B.N Gupta – Statistics
- S.P Singh – statistics
- Gupta and Kapoor – Statistics
- Yule and Kendall – Statistics method