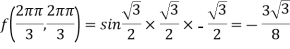UNIT–4
Differential Calculus
Important definitions-
Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a , if
Differentiability- A function f(x) is said to be differentiable at x=a if
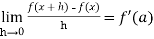exists where ‘a’ belongs to I
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists at least a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
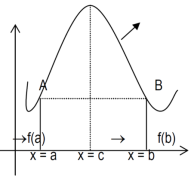
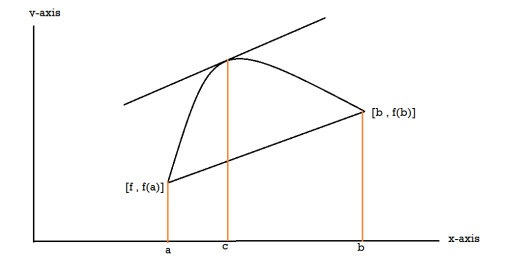
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
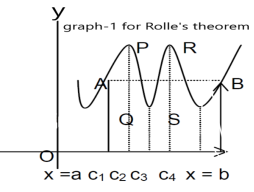
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example: Verify Rolle’s theorem for the function f(x) = x(x+3)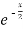 
in interval [-3 , 0].
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x) 
+ (2x + 3)
= 
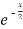
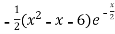
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
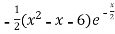= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Example: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+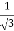 
and 2 -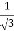 
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Example: Verify the Rolle’s theorem for sin x in the interval [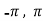
]
Sol. Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now , f’(x) = cos x exists for all x in (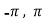
) and
f(
0
f(
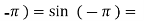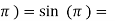0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives , cos x = 0
x =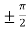 
Here we notice that both intervals lie in (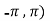
.
There exists, c =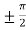 
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Lagrange’s mean value theorem-
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a , b]
2. If it is differentiable in (a , b)
Then there atleast exists a value cϵ (a , b)
f’(c) =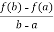 
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that, g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab ,
Which gives,
A =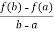 
…………………..(2)
As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,, f’(c) = A,
From equation (2) , we get
f’(c) =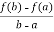 
hence proved.
Example: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) =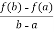 
= 
= 
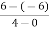= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2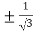 
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Example: : Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].
Sol. We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) =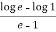 
, let x = c,
Then ,
f’(c) =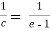 
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem.
Taylor’s theorem for a function f(x) can be expressed as an infinite series as follows-
f(x) = f(a) + (x – a)f’(a) +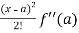 
+ ………
.
Example: Expand the function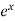 
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) +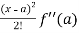 
+ ………
. ………….(1)
Here f(x) =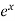 
and a = 1
Now,
f’(x) = 
and f’(a) = e
f’’(x) =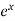 
and f’’(a) = e
Put these values in equation (1),
…………….
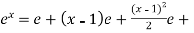Take ‘e’ as common,
…………….}
Which is the required expansion.
Example: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 
+ ………
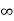. ………….(1)
Here ,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now , we will find out the derivatives ,
f’(x) = 6x – 6 and f’(3) = 12
f’’(x) = 6 and f’’(3) = 6
f’’’(x) = 0 and f’’’(x) = 14
Put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6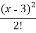 
+…………. Ans.
Let we have two functions f(x) and g(x) and-
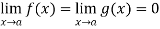
Then-
is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Now, Let we have two functions f(x) and g(x) and-
Then-
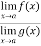is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Some other indeterminate forms are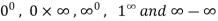 
L’Hospital’s rule for 
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type 
.
(note- we can not apply L’Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives .if the limit is finite ,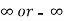
then it is equal to the limit of f(x)/g(x).
Example-1: Evaluate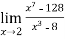 
Sol. Here we notice that it is an indeterminate form of 
.
So that , we can apply L’Hospital rule-
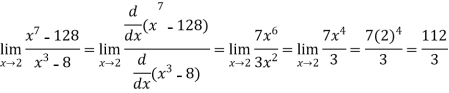
Example-2: Evaluate 
.
Sol. Let f(x) =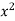 
and g(x) = 
.
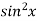Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
= 
= 
= 
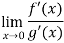
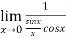
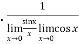= 1
Note- Suppose we get an indeterminate form even after finding first derivative, then in that case , we use the other form of L’Hospital’s rule.
If we have f(x) and g(x) are two functions such that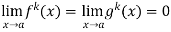 
.
If 
exist or (∞ , -∞), then
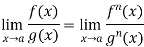
Example-3: Evaluate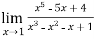 
Sol. Let f(x) =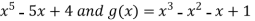 
, then
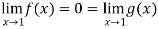
And
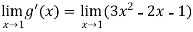= 0
= 0
But if we use L’Hospital rule again, then we get-
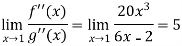
Example-4: Evaluate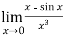 
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get
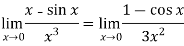
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
= 
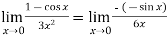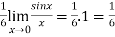
L’Hospital’s rule for 
form-
Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that
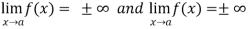
If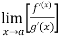 
has a finite limit, or if it is 
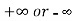, then
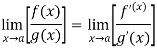
Theorem- If we have f(x) and g(x) are two functions such that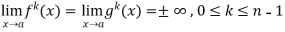 
.
If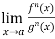 
exist or (∞ , -∞), then
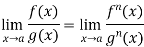
Example-5: Find 
, n>0.
Sol. Let f(x) = log x and g(x) =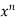 
These two functions satisfied the theorem that we have discussed above-
So that,
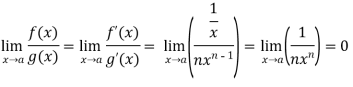
Example-6: Evaluate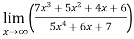 
Sol. Apply L’Hospital rule as we can see that this is the form of 
= 
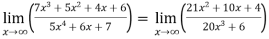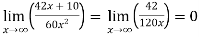
Example-7:
Note- In some cases like above example, we can not apply L’Hospital’s rule.
Other types of indeterminate forms-
Example-8: Evaluate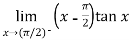 
Sol. Here we find that-
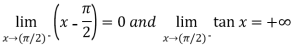
So that this limit is the form of 0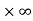
.
Now,
Change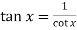 
to obtain the limit-
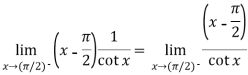
Now this is the form of 0/0,
Apply L’Hospital’s rule-
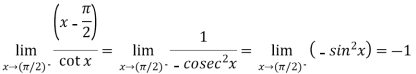
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point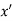 
if and only if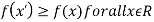 
Minima is a minimum point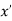 
if and only if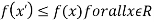 
Maxima and Minima of a function of two independent variables
Let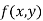 
be a defined function of two independent variables.
Then the point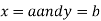 
is said to be a maximum point of 
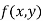if
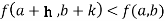
Or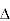 
= 
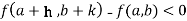
For all positive and negative values of h and k.
Similarly the point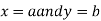 
is said to be a minimum point of 
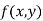if
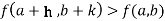
Or 
= 
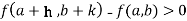
For all positive and negative values of h and k.
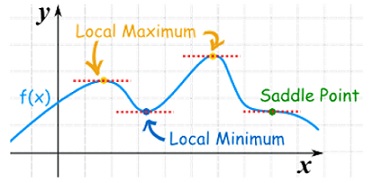
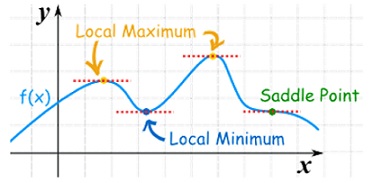
Saddle point:Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643288323_993638.png)
At the point.
Stationary Value
The value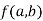 
is said to be a stationary value of 
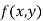if
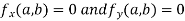
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of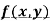 
- Calculate
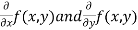. - Form and solve
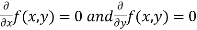, we get the value of x and y let it be pairs of values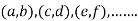 
- Calculate the following values :
4. (a) If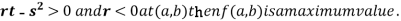 
(b) If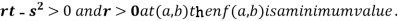 
(c) If 
(d) If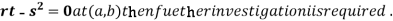 
Example1 Find out the maxima and minima of the function
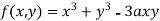
Given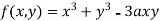 
…(i)
Partially differentiating (i) with respect to x we get
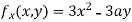….(ii)
Partially differentiating (i) with respect to y we get
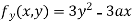….(iii)
Now, form the equations 
Using (ii) and (iii) we get
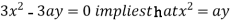
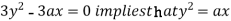
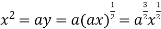using above two equations
Squaring both side we get
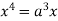
Or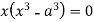 
This show that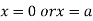 
Also we get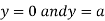 
Thus we get the pair of value as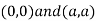 
Now, we calculate
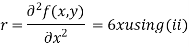
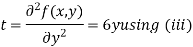
Putting above values in
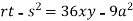
At point (0,0) we get
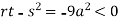
So, the point (0,0) is a saddle point.
At point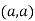 
we get
So the point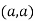 
is the minimum point where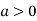 
In case 
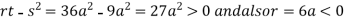
So the point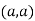 
is the maximum point where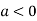 
Example2 Find the maximum and minimum point of the function
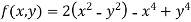
Partially differentiating given equation with respect to and x and y then equate them to zero
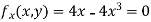
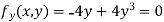
On solving above we get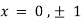 
Also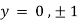 
Thus we get the pair of values (0,0), (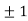
,0) and (0,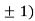
Now, we calculate
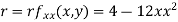
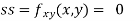
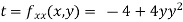
At the point (0,0)
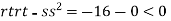
So function has saddle point at (0,0).
At the point (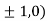
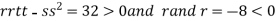
So the function has maxima at this point (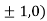
.
At the point (0,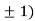
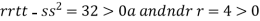
So the function has minima at this point (0,
.
At the point (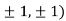
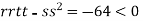
So the function has an saddle point at (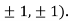
Example3 Find the maximum and minimum value of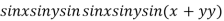 
Let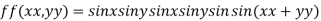 
Partially differentiating given function with respect to x and y and equate it to zero
..(i)
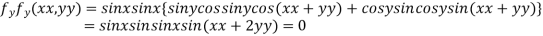..(ii)
On solving (i) and (ii) we get
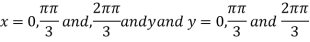
Thus pair of values are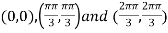 
Now, we calculate
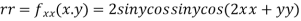
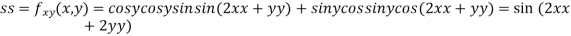
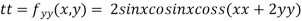
At the point (0,0)
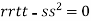
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x,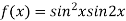 
At the point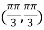 
So that the given function has maximum value at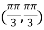 
Therefore maximum value of given function
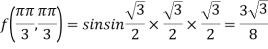
At the point 
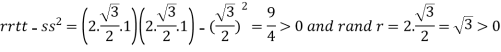
So that the given function has minimum value at 
Therefore minimum value of the given function
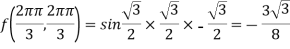
UNIT–4
Differential Calculus
Important definitions-
Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a , if
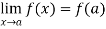
Differentiability- A function f(x) is said to be differentiable at x=a if
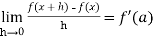exists where ‘a’ belongs to I
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists at least a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
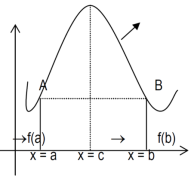
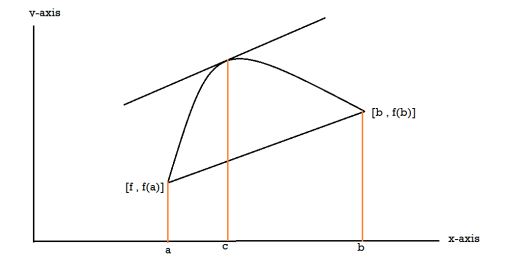
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
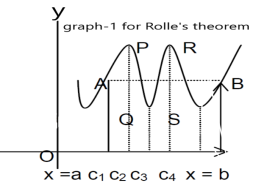
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example: Verify Rolle’s theorem for the function f(x) = x(x+3)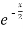 
in interval [-3 , 0].
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x)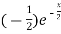 
+ (2x + 3)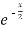
= 
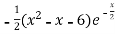
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
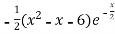= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Example: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+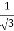 
and 2 -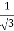 
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Example: Verify the Rolle’s theorem for sin x in the interval [
]
Sol. Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now , f’(x) = cos x exists for all x in (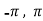
) and
f(
0
f(
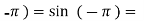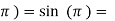0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives , cos x = 0
x =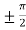 
Here we notice that both intervals lie in (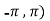
.
There exists, c =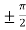 
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Lagrange’s mean value theorem-
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a , b]
2. If it is differentiable in (a , b)
Then there atleast exists a value cϵ (a , b)
f’(c) =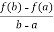 
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that, g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab ,
Which gives,
A =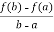 
…………………..(2)
As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,, f’(c) = A,
From equation (2) , we get
f’(c) =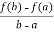 
hence proved.
Example: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) =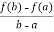 
= 
= 
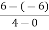= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2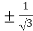 
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Example: : Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].
Sol. We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) = 
, let x = c,
Then ,
f’(c) = 
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem.
Taylor’s theorem for a function f(x) can be expressed as an infinite series as follows-
f(x) = f(a) + (x – a)f’(a) +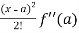 
+ ………
.
Example: Expand the function 
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) +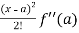 
+ ………
. ………….(1)
Here f(x) = 
and a = 1
Now,
f’(x) =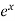 
and f’(a) = e
f’’(x) =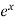 
and f’’(a) = e
Put these values in equation (1),
…………….
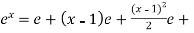Take ‘e’ as common,
…………….}
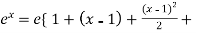Which is the required expansion.
Example: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 
+ ………
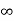. ………….(1)
Here ,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now , we will find out the derivatives ,
f’(x) = 6x – 6 and f’(3) = 12
f’’(x) = 6 and f’’(3) = 6
f’’’(x) = 0 and f’’’(x) = 14
Put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6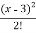 
+…………. Ans.
Let we have two functions f(x) and g(x) and-
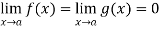
Then-
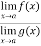is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Now, Let we have two functions f(x) and g(x) and-
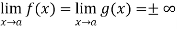
Then-
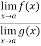is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Some other indeterminate forms are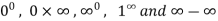 
L’Hospital’s rule for 
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type 
.
(note- we can not apply L’Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives .if the limit is finite ,
then it is equal to the limit of f(x)/g(x).
Example-1: Evaluate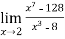 
Sol. Here we notice that it is an indeterminate form of 
.
So that , we can apply L’Hospital rule-
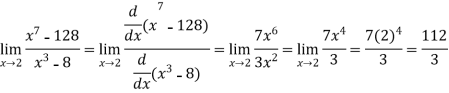
Example-2: Evaluate 
.
Sol. Let f(x) = 
and g(x) =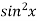 
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
= 
= 
= 
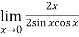
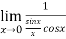
= 1
Note- Suppose we get an indeterminate form even after finding first derivative, then in that case , we use the other form of L’Hospital’s rule.
If we have f(x) and g(x) are two functions such that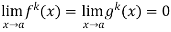 
.
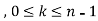If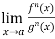 
exist or (∞ , -∞), then
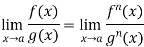
Example-3: Evaluate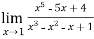 
Sol. Let f(x) = 
, then
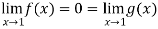
And
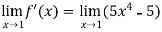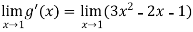= 0
= 0
But if we use L’Hospital rule again, then we get-
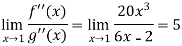
Example-4: Evaluate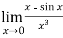 
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get
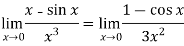
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
= 
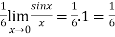
L’Hospital’s rule for 
form-
Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that
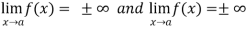
If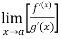 
has a finite limit, or if it is 
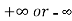, then
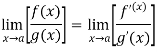
Theorem- If we have f(x) and g(x) are two functions such that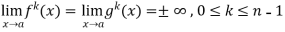 
.
If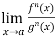 
exist or (∞ , -∞), then
Example-5: Find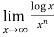 
, n>0.
Sol. Let f(x) = log x and g(x) =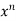 
These two functions satisfied the theorem that we have discussed above-
So that,
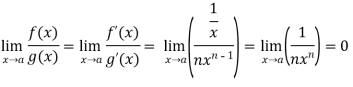
Example-6: Evaluate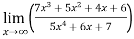 
Sol. Apply L’Hospital rule as we can see that this is the form of 
= 
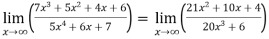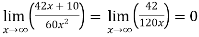
Example-7:
Note- In some cases like above example, we can not apply L’Hospital’s rule.
Other types of indeterminate forms-
Example-8: Evaluate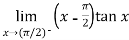 
Sol. Here we find that-
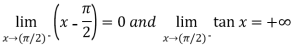
So that this limit is the form of 0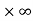
.
Now,
Change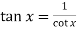 
to obtain the limit-
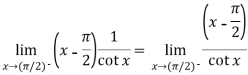
Now this is the form of 0/0,
Apply L’Hospital’s rule-
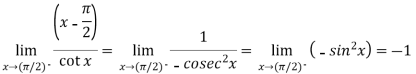
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point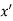 
if and only if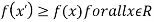 
Minima is a minimum point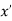 
if and only if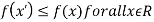 
Maxima and Minima of a function of two independent variables
Let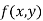 
be a defined function of two independent variables.
Then the point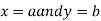 
is said to be a maximum point of 
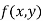if
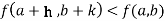
Or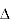 
= 
For all positive and negative values of h and k.
Similarly the point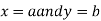 
is said to be a minimum point of 
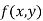if
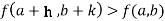
Or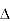 
= 
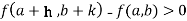
For all positive and negative values of h and k.
Saddle point:Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643288341_9303942.png)
At the point.
Stationary Value
The value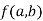 
is said to be a stationary value of 
if
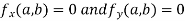
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of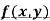 
- Calculate
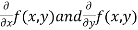. - Form and solve
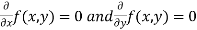, we get the value of x and y let it be pairs of values 
- Calculate the following values :
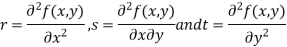
4. (a) If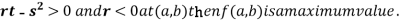 
(b) If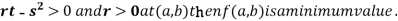 
(c) If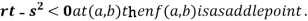 
(d) If 
Example1 Find out the maxima and minima of the function
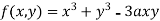
Given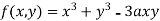 
…(i)
Partially differentiating (i) with respect to x we get
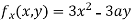….(ii)
Partially differentiating (i) with respect to y we get
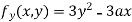….(iii)
Now, form the equations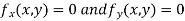 
Using (ii) and (iii) we get
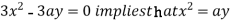
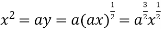using above two equations
Squaring both side we get
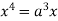
Or 
This show that 
Also we get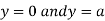 
Thus we get the pair of value as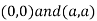 
Now, we calculate
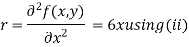
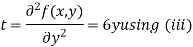
Putting above values in
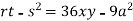
At point (0,0) we get
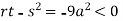
So, the point (0,0) is a saddle point.
At point 
we get
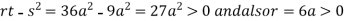
So the point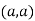 
is the minimum point where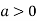 
In case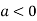 
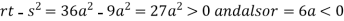
So the point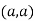 
is the maximum point where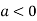 
Example2 Find the maximum and minimum point of the function
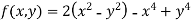
Partially differentiating given equation with respect to and x and y then equate them to zero
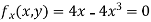
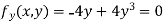
On solving above we get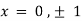 
Also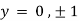 
Thus we get the pair of values (0,0), (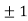
,0) and (0,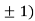
Now, we calculate
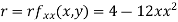
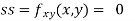
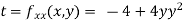
At the point (0,0)
So function has saddle point at (0,0).
At the point (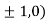
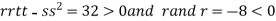
So the function has maxima at this point (
.
At the point (0,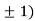
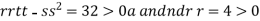
So the function has minima at this point (0,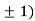
.
At the point (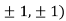
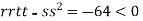
So the function has an saddle point at (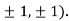
Example3 Find the maximum and minimum value of 
Let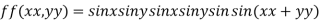 
Partially differentiating given function with respect to x and y and equate it to zero
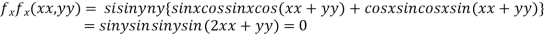..(i)
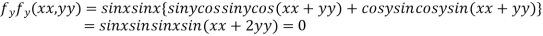..(ii)
On solving (i) and (ii) we get
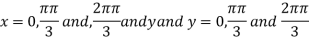
Thus pair of values are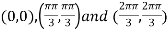 
Now, we calculate
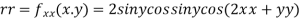
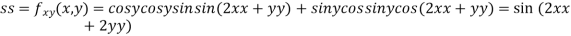
At the point (0,0)
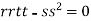
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x,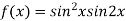 
At the point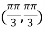 
So that the given function has maximum value at 
Therefore maximum value of given function
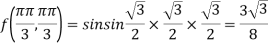
At the point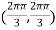 
So that the given function has minimum value at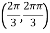 
Therefore minimum value of the given function
