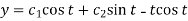UNIT–2
Linear differential equations of higher order
2.1. Non-Homogeneous equations of higher order with constant coefficient of R.H.S. Terms of the type 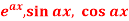
Linear differential equation are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus the general linear differential equation of the n’th order is of the form
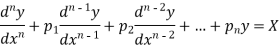
Where 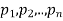 and X are function of x.
and X are function of x.
Linear differential equation with constant co-efficient are of the form-
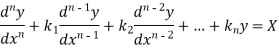
Where 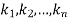 are constants.
are constants.
Rules to find the complementary function-
To solve the equation-
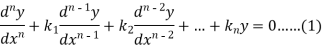
This can be written as in symbolic form-
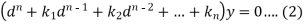
Or-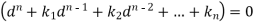
It is called the auxiliary equation.
Let 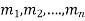 be the roots-
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,
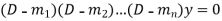
Now this equation will be satisfied by the solution of 
This is a Leibnitz’s linear and I.F. = 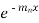
Its solution is-
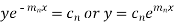
The complete solution will be-
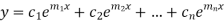
Case-2: If two roots are equal 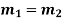
Then complete solution is given by-
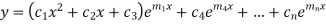
Case-3: If one pair of roots be imaginary, i.e. 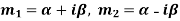 then the complete solution is-
then the complete solution is-
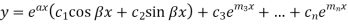
Where 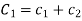 and
and 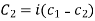
Case-4: If two points of imaginary roots be equal-
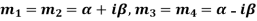
Then the complete solution is-

Example-Solve 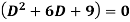
Sol.
Its auxiliary equation is-
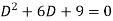
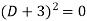
Where-
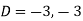
Therefore the complete solution is-
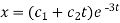
Inverse operator-
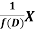 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
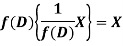
So that 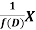 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 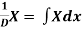
2. 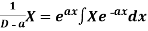
Rules for finding the particular integral-
Let us consider the equation-
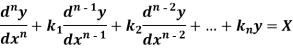
Or in symbolic form-
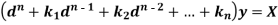
So that-
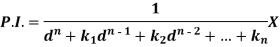
Now-
Case-1: When X = 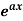
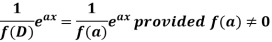
In case f(a) = 0, then we see that the above rule will not work,
So that-
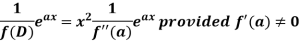
Example: Find the P.I. Of (D + 2)
Sol.
P.I. = 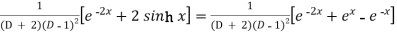
Now we will evaluate each term separately-
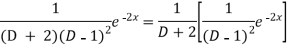
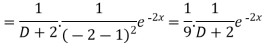
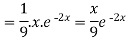
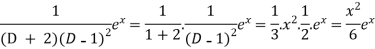
And
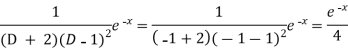
Therefore-
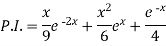
Example: Solve (D – D’ – 2 ) (D – D’ – 3) z = 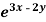
Sol.
The C.F. Will be given by-
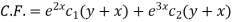
Particular integral-
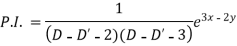
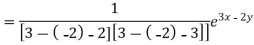
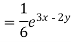
Therefore the complete solution is-

Case-2: when X = sin(ax + b) or cos (ax + b)

In case 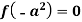 then the above rule fails.
then the above rule fails.
Now-
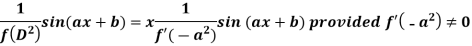
And if 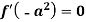
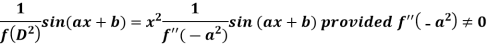
Similarly-
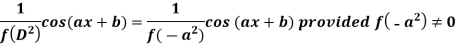
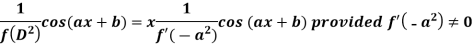
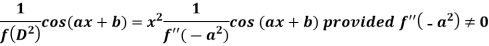
Example: Find the P.I. Of 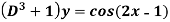
Sol.
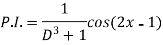
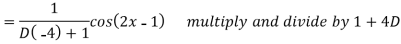
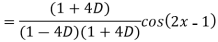
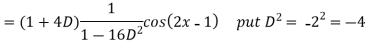
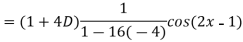

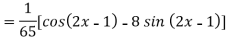
Example: Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
Sol.
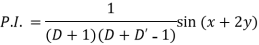

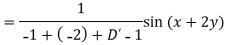
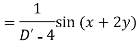
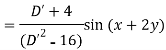
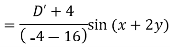
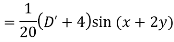
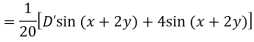
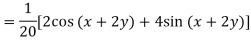
Example: Find P.I. Of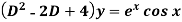
Sol. P.I = 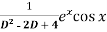
Replace D by D+1
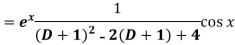

Put 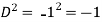
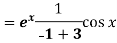
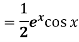
2.2. Polynomials in x, 
Let us consider the equation-
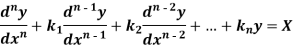
Or in symbolic form-
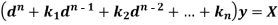
So that-
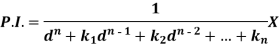
Now-
Case-1: When 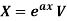 , V is the function of x.
, V is the function of x.
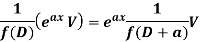
Case-2: When X is any other function of x.
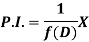
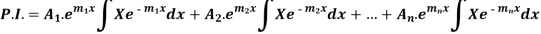
Example: Find P.I. Of 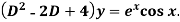
Sol.
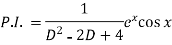
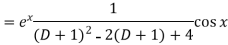
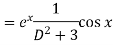
Put 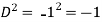
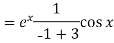
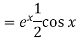
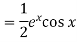
Working method to find the complete solution of an equation-
Example: Solve 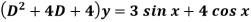
Sol.
Here first we will find the C.F.-
Its auxiliary equation will be-
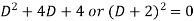
Here we get-
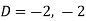
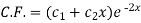
Now we will find P.I.-
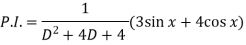
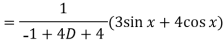
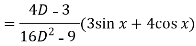
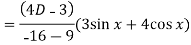
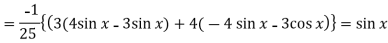
Now the complete solution is-

Example: Solve-
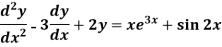
Sol.
The given equation can be written as-
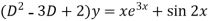
Its auxiliary equation is-
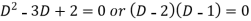
We get-
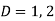
So that the C.F. Will be-
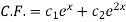
Now we will find P.I.-
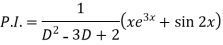
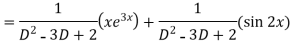
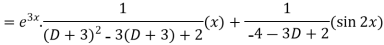
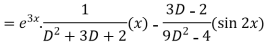
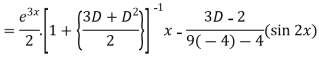
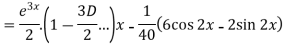
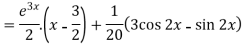
Therefore the complete solution is-
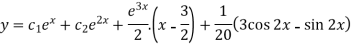
Method of variation of parameters-
Consider a second order LDE with constant co-efficients given by

Then let the complimentary function 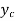 is given by
is given by
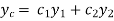
Then the particular integral is
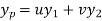
Where u and v are unknown and to be calculated using the formula
u=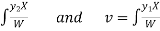
Example-1: Solve the following DE by using variation of parameters-
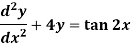
Sol. We can write the given equation in symbolic form as-
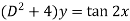
To find CF-
It’s A.E. Is 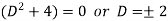
So that CF is- 
To find PI-
Here 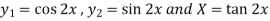
Now 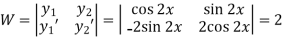
Thus PI = 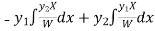
= 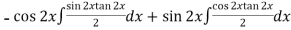
= 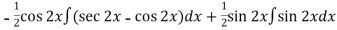
= 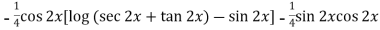
= 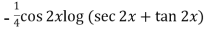
So that the complete solution is-
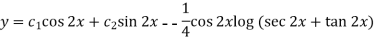
Example-2: Solve the following by using the method of variation of parameters.
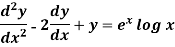
Sol. This can be written as-

C.F.-
Auxiliary equation is- 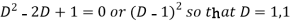
So that the C.F. Will be- 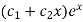
P.I.-
Here 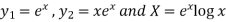
Now 
Thus PI = 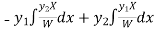
= 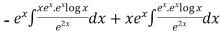
= 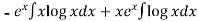

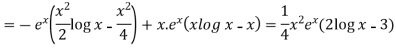
So that the complete solution is-

Cauchy’s and Legendre’s DE
An equation of the form
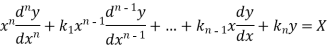
Here X is the function of x, is called Cauchy’s homogeneous linear equation.
Example-1: Solve 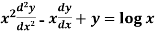
Sol. As it is a Cauchy’s homogeneous linear equation.
Put 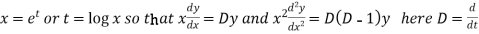
Then the equation becomes [D(D-1)-D+1]y = t or 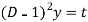
Auxiliary equation-
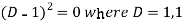
So that-
C.F.=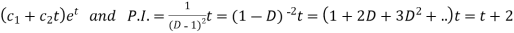
Hence the solution is- 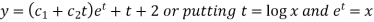 , we get-
, we get-
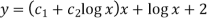
Example-2: Solve 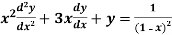
Sol. On putting  so that,
so that,
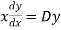 and
and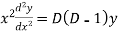
The given equation becomes-
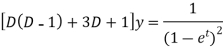
Or it can be written as-
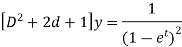
So that the auxiliary equation is- 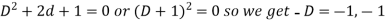
C.F. = 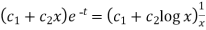
Particular integral- 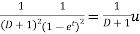
Where 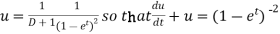
It’s a Leibnitz’s linear equation having I.F.=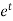
Its solution will be-
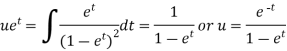
P.I. = 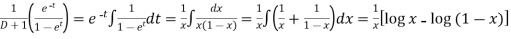
= 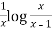
So that the complete solution is-
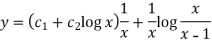
An equation of the form-
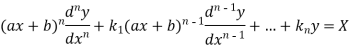
Is called Legendre’s linear equation.
Example-3: Solve 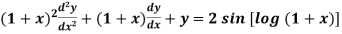
Sol. As we see that this is a Legendre’s linear equation.
Now put 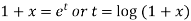
So that- 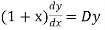
And 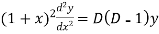
Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t
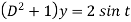
Its auxiliary equation is- 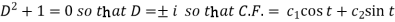
And particular integral-
P.I. = 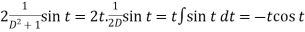
Note - 
Hence the solution is -