Unit–1
Differential equation of first order and first degree
A differential equation of the form
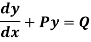
Is called linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Working rule
(1)Convert the equation to the standard form 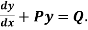
(2) Find the integrating factor.
(3) Then the solution will be y(I.F) = 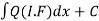
Example-1: Solve-
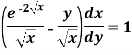
Sol. We can write the given equation as-
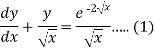
So that-
I.F. = 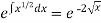
The solution of equation (1) will be-
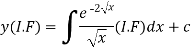
Or
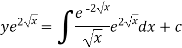
Or
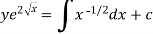
Or
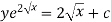
Example-2: Solve-

Sol.
We can write the equation as-

We see that it is a Leibnitz’s equation in x-
So that-
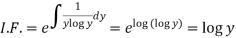
Therefore the solution of equation (1) will be-
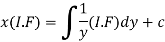
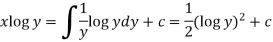
Or
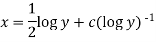
Example-3: Solve sin x 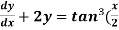 )
)
Solution: here we have,
Sin x 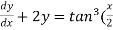 )
)
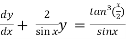 which is the linear form,
which is the linear form,
Now,
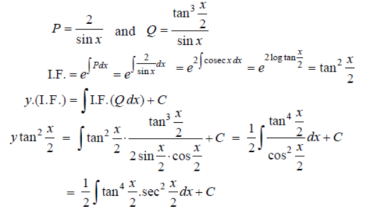
Put tan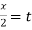 so that
so that  sec²
sec² dx = dt, we get
dx = dt, we get

Which is the required solution.
Bernoulli’s equation-
The equation
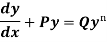
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation -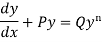
By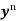 , so that
, so that
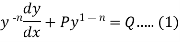
Put 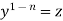 so that
so that 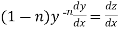
Then equation (1) becomes-
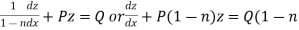 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve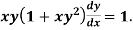
Sol.
We can write the equation as-
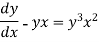
On dividing by 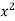 , we get-
, we get-
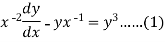
Put 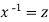 so that
so that 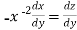
Equation (1) becomes,
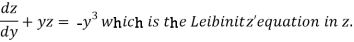
Here,
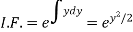
Therefore the solution is-

Or
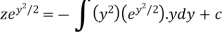
Now put 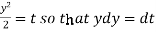
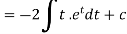
Integrate by parts-
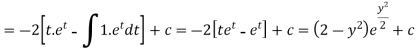

Or
Example: Solve 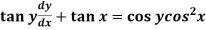
Sol. Here given,
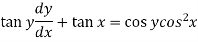
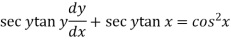
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
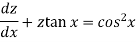
Here,
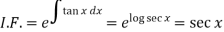
Then the solution will be-


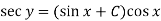
Example: Solve- 
Sol. Here given-
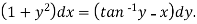
We can re-write this as-
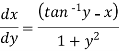

Which is a linear differential equation-
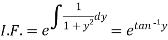
The solution will be-
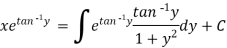
Put 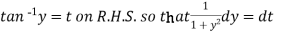
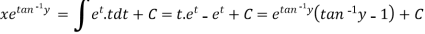
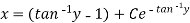
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
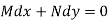
Is called an exact differential equation if it satisfies the following condition-
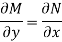
Here 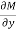 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 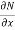 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
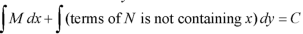
Example-1: Solve 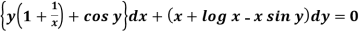
Sol.
Here M = 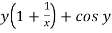 and N =
and N = 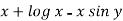
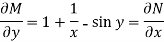
Then the equation is exact and its solution is-
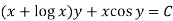
Example-2: Solve-
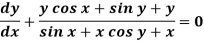
Sol. We can write the equation as below-
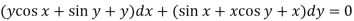
Here M = 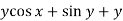 and N =
and N = 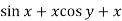
So that-
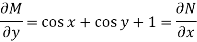
The equation is exact and its solution will be-
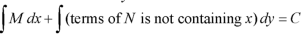
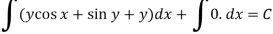
Or
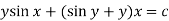
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
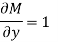
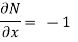
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Equation reducible to exact form-
1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor.
Example: Solve-
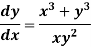
Sol.
We can write the given equation as-
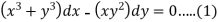
Here,
M = 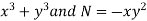

Multiply equation (1) by  we get-
we get-
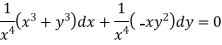
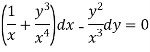
This is an exact differential equation-

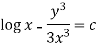
2. I.F. For an equation of the type 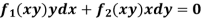
IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.
Example: Solve-
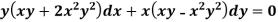
Sol.
Here we have-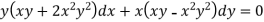
Now divide by xy, we get-
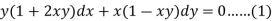
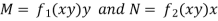
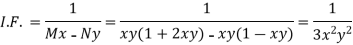
Multiply (1) by 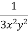 , we get-
, we get-
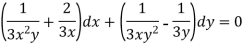
Which is an exact differential equation-

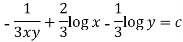
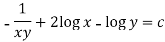
3. In the equation M dx + N dy = 0,
(i) If 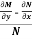 be a function of x only = f(x), then
be a function of x only = f(x), then 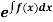 is an integrating factor.
is an integrating factor.
(ii) If 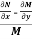 be a function of y only = F(x), then
be a function of y only = F(x), then 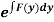 is an integrating factor.
is an integrating factor.
Example: Solve-
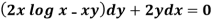
Sol.
Here given,

M = 2y and N = 2x log x - xy
Then-
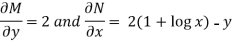
Here,
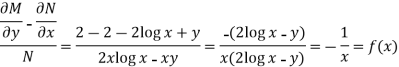
Then,
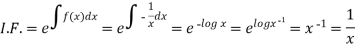
Now multiplying equation (1) by 1/x, we get-
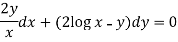
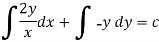
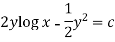
4. For the following type of equation-
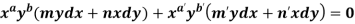
An I.F. Is 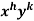
Where-
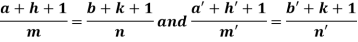
Example: Solve-
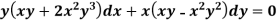
Sol.
We can write the equation as below-
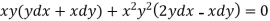
Now comparing with-
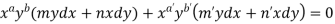
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 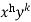
Where-
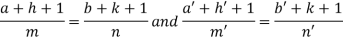
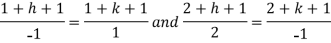
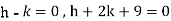
On solving we get-
h = k = -3
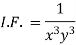
Multiply the equation by 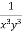 , we get-
, we get-
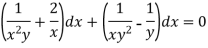
It is an exact equation.
So that the solution is-

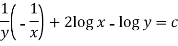
“When every curve of either family cuts each curve of other family at right angle in the two families of curve, then they are orthogonal trajectories of each other.”
Ex. 1. The line of heat flow is perpendicular to isothermal curve.
Steps to find orthogonal trajectories of curves-:
1. Differentiate the equation of the curve and find the differential equation as below-
f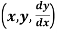 = 0
= 0
2. Replace  by
by 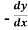
3. Solve the differential equation of the orthogonal trajectories,
f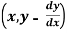 = 0
= 0
Self-orthogonal - if the family of orthogonal traj. Is same as the family of curves, then it is called self-orthogonal.
Example: if the family of curves is xy = c , then find its orthogonal trajectory.
Sol. First we will differentiate the given equation with respect to x,
We get,
y + x 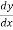 = 0
= 0
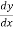 =
= 
Replace  by
by 
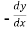 =
= 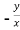
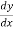 =
= 
We get,
Ydy = x dx
Now integrate this equation, we get
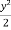 =
=  + c
+ c
y² - x² = 2c. Ans.
Example: find the orthogonal trajectory of the family of curves x² - y² = c
Sol. Here we will follow same procedure as we did in above example,
Diff. The given equation w.r.t. x, we get
2x – 2y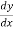 = 0
= 0
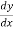 =
= 
Replace  by
by 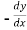
 =
= 
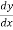 = -
= - 
Ydy = - xdx
Now integrate the above eq.
 =
= 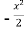 + c
+ c
On solving we get,
x² + y² = 2c.
Newton’s law of cooling-
Definition- The temperature of a body changes at a rate which is proportional to the difference in temperature between that of the surrounding medium and that of the body itself.
If 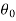 is the temperature of the surroundings and
is the temperature of the surroundings and 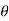 that of the body at any time t, then-
that of the body at any time t, then-
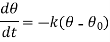
Here k is a constant.
Example: A body originally at 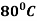 cools down to
cools down to 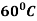 in 20 minutes. The temperature of the air being
in 20 minutes. The temperature of the air being 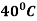 . What will be the temperature of the body after 40 minutes from the original?
. What will be the temperature of the body after 40 minutes from the original?
Sol.
If  is the temperature of the surroundings and
is the temperature of the surroundings and 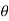 that of the body at any time t, then-
that of the body at any time t, then-
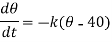
On integrating-
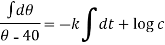
Or
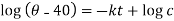
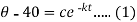
When t = 0 and 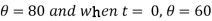
So that-
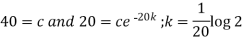
Then equation-1 becomes-

When t = 40 min, then-
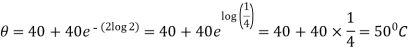
Exponential growth
Let p (t) increases with the time t and the rate of increase is proportional to P
Then,
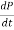 = kP
= kP
Here, k>0 and t time is the time.
The solution is given by,
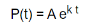
Rate of decay-
According to this law-
The disintegration at any instant is proportional to the amount of material present of material at any time t, then-

Here k is a constant.