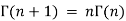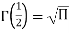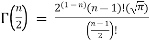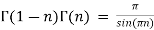Unit 5
Multiple Integral and special function
Definition: evaluating triple integrals is similar to evaluating nested functions: you work from inside out. Triple integrals look scary, but if you take them step by step, they’re no kore difficult than regular integrals. You start in the centre and work your way out. For example, begin by separating two inner integrals.
Example 1: evaluate the following:
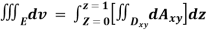
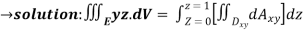
= 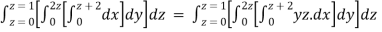
= 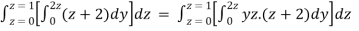
= 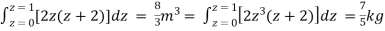
Example 2: evaluate the following:
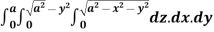
Solution: let I = 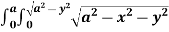 .dxdy
.dxdy
= 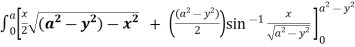
= 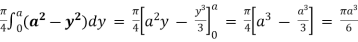
Example 3: evaluate the following triple integral
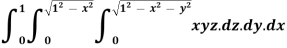
Solution: let I = 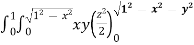 .dzdydx
.dzdydx
= 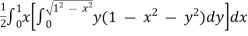
= 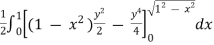
= 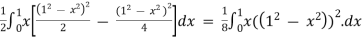
= 
Example 1: evaluate 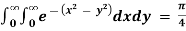 by changing to polar co-ordinates hence evaluate
by changing to polar co-ordinates hence evaluate 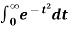
Solution: let I = 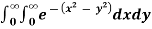
Polar form: x = rcos , y= rsin
, y= rsin dx dy = r. Dr d
dx dy = r. Dr d
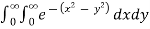
= 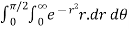
= 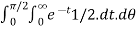
= ½ 
= -1/2 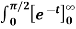
= - ½ 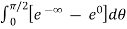
= -1/2 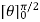 = ½ (
= ½ (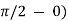
= 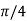 …(1)
…(1)
To find 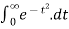
By equation 1.,
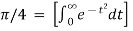
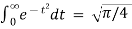 =
= 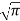 /2.
/2.
Example 2: express 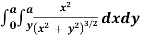 in polar cartesian form hence evaluate it
in polar cartesian form hence evaluate it
Solution: let cartesian form I= 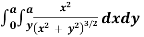 where
where
X varies from x = y to x = a
Y varies from y = 0 to y = a
Polar form: x = rcos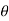 , y= rsin
, y= rsin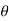 dx dy = r. Dr d
dx dy = r. Dr d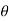
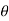 varies from
varies from 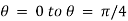
I = 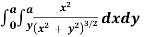
= 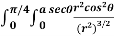 r.dr. d
r.dr. d
= 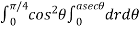
=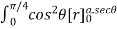
= 
=a
= a
= 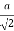
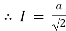
Definition: spherical and cylindrical coordinate systems: These systems are three-dimensional relatives of the two-dimensional polar coordinate system. Cylindrical coordinates are more straight forward to understand than spherical and are similar to the three-dimensional cartesian system (X, Y, Z).
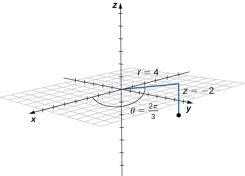
Example 1: plot the point with cylindrical co-ordinates (4, 2 /3, -2) and express its location in rectangular coordinates.
/3, -2) and express its location in rectangular coordinates.
Solution: conversion from cylindrical to rectangular coordinates requires a simple application.
x = r cos = 4 cos (2
= 4 cos (2 /3) = -2
/3) = -2
y = r sin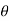 = 4sin (2
= 4sin (2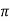 /3) = 2/
/3) = 2/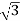 .
.
Z = -2
The point with cylindrical co-ordinates (4, 2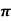 /3, -2) has rectangular coordinates (-2, 2/
/3, -2) has rectangular coordinates (-2, 2/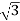 , -2) seen in the diagram.
, -2) seen in the diagram.
Example 2: convert the rectangular co-ordinates (1, -3, 5) to cylindrical co-ordinates.
Solution: use the second set of equations from note to translate from rectangular to cylindrical co-ordinates
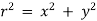
r = 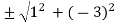
= 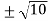
We choose the positive square root, so r = 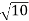 . Now, we apply the formula to find
. Now, we apply the formula to find 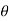 . In this case, y is negative and x is positive, which means we must select the value
. In this case, y is negative and x is positive, which means we must select the value 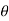 between
between 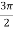 and 2
and 2
Tan =
=  =
= 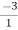
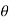 = arctan (-3)
= arctan (-3) 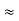 5.03 rad.
5.03 rad.
In this case the z-coordinates are the same in both rectangular and cylindrical coordinates: z = 5.
The point with rectangular co-ordinates (1, -3, 5) has cylindrical coordinates approximately equal to (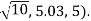
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral
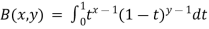
For complex number inputs x, y such that Re x > 0, Re y > 0.
Gamma properties:
Beta properties:
 (m, n) = B (n, m)
(m, n) = B (n, m) (m, n) =
(m, n) = 
 (m, n) =
(m, n) = 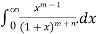
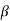 (m, n) =
(m, n) = 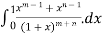
Example 1: f(B) =  Solve the given function.
Solve the given function.
Solution: 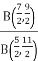 =
= 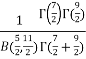
= 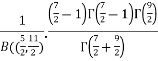 [Recursive function for the gamma function]
[Recursive function for the gamma function]
= 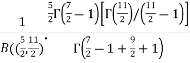 [Recursive formula for the gamma function]
[Recursive formula for the gamma function]
=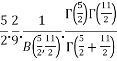
=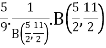 [By the definition of Beta function]
[By the definition of Beta function]
= 
Example 2: B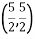 =
=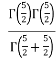
= 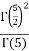
= 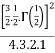
=
=  [because
[because 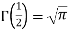 ]
]
BETA FUNCTION MORE PROBLEMS
Relation between Beta and Gamma functions:
Relation between beta and gamma function is defined by:
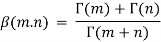
Example 1: evaluate I = 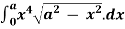
Solution: let x2 = a2 y, we get
I = 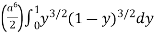
= 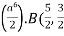 )
)
= 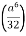 .
.
Example 2: Evaluate I = 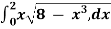
Solution: let 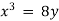
I = 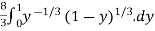
= 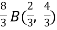
= 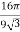 .
.
Example 3: prove that 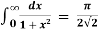
Solution: let I = 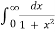
Put 
= 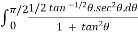
= 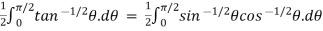 .
.
=  = ¼.
= ¼. 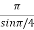 =
=  .
.
Textbooks:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 10/e, John Wiley & Sons, 2011.
2. B. S. Grewal, Higher Engineering Mathematics, 44/e, Khanna Publishers, 2017.
References:
1. R. K. Jain and S. R. K. Iyengar, Advanced Engineering Mathematics, 3/e, Alpha Science
International Ltd., 2002.
2. George B. Thomas, Maurice D. Weir and Joel Hass, Thomas Calculus, 13/e, Pearson
Publishers, 2013.
3. Glyn James, Advanced Modern Engineering Mathematics, 4/e, Pearson publishers, 201.