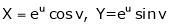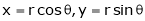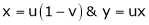Unit 3
Multivariable calculus
First order partial differentiation-
Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 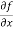 and defined as follows:
and defined as follows:
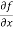 =
= 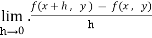
Now the partial derivative of f with respect to f can be written as 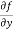 and defined as follows:
and defined as follows:
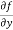 =
= 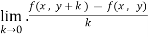
Note: a. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
b. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a)  =
= 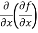
(b) 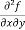 =
= 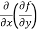
(c) 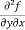 =
= 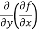
(d) 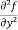 =
= 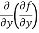
b and c are known as mixed partial derivatives.
Similarly, we can find the other higher order derivatives.
Example-1: -Calculate 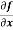 and
and 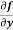 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Solution: To calculate 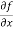 treat the variable y as a constant, then differentiate
treat the variable y as a constant, then differentiate
f(x, y) with respect to x by using differentiation rules,
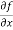 =
= 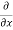 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 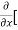 3x³] -
3x³] - 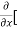 5y²] +
5y²] + 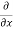 [2xy] -
[2xy] - 8x] +
8x] +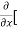 4y] -
4y] - 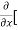 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
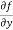 =
= 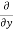 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 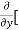 3x³] -
3x³] - 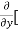 5y²] +
5y²] +  [2xy] -
[2xy] -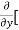 8x] +
8x] +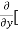 4y] -
4y] - 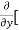 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate  and
and 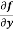 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Solution: To calculate  treat the variable y as a constant, then differentiate
treat the variable y as a constant, then differentiate
f(x, y) with respect to x by using differentiation rules,
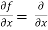 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)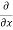 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
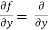 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)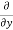 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xycos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f(x, y) = ( x³y² - x y⁵)
Solution: 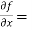 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
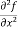 =
= 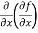 = 6xy²
= 6xy²
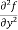 =
= 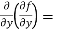 2x³ - 20xy³
2x³ - 20xy³
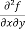 =
= 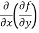 = 6x²y – 5y⁴
= 6x²y – 5y⁴
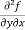 =
= 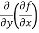 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find
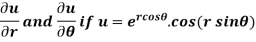
Solution: First we will differentiate partially with respect to r,
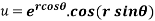
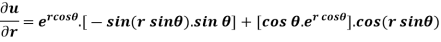
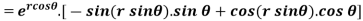

Now differentiate partially with respect to θ, we get
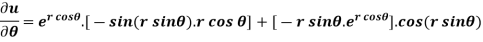

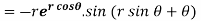
Example-5: if, 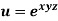 then find
then find 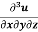
Solution:
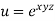
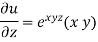
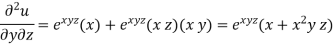
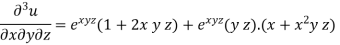
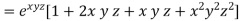
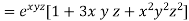
Example-6: if 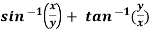 , then show that-
, then show that- 
Solution: Here we have,
u = 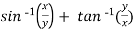 ………………….,.(1)
………………….,.(1)
Now partially differentiate eq.(1) w.r to x and y , we get
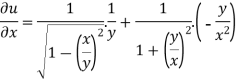
= 
Or
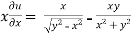 ……………….,(2)
……………….,(2)
And now,
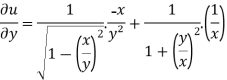
= 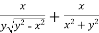
 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
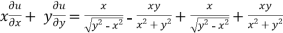 = 0
= 0
Hence proved.
When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant.
Let the function, u = f( x, y), such that x = g(t) , y = h(t)
Then we can write,
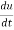 =
= 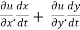
= 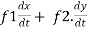
This is the total derivative of u with respect to t.
Change of variable-
If w = f (x, y) has continuous partial variables fx and fy and if x = x (t), y = y (t) are
Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a
Differentiable function of t.
In this case, we get,
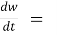 fx (x (t), y (t)) x’(t)+ fy (x(t), y (t)) y’(t).
fx (x (t), y (t)) x’(t)+ fy (x(t), y (t)) y’(t).
Example-:1 let q = 4x + 3y and x = t³ + t² + 1, y = t³ - t² - t
Then find 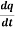 .
.
Solution: 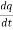 . =
. = 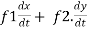
Where, f1 = 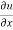 , f2 =
, f2 = 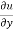
In this example f1 = 4, f2 = 3
Also,
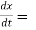 3t² + 2t ,
3t² + 2t , 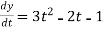
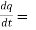 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(
= 21t² + 2t – 3
Example-2: Find 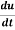 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Solution: As we know that by definition, 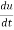 =
= 
 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Example-3: if w = x² + y – z + sintan x + y = t, find
(a) 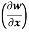 y, z
y, z
(b) 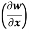 t, z
t, z
Solution: With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
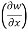 y, z = 2x + cos(x+y)
y, z = 2x + cos(x+y)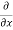 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus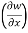 t, z = 2x - 1
t, z = 2x - 1
Example-4: If u = u (y – z, z - x, x – y) then prove that 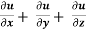 = 0
= 0
Solution: Let, r = y - z, s = z - x, t = x – y, u = u(r, s, t)
Then,

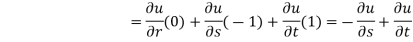
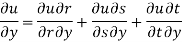
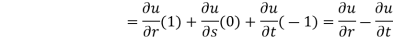
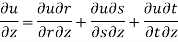
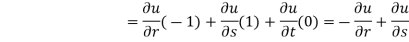
By adding all these equations, we get,
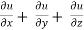 = 0 hence proved.
= 0 hence proved.
Example-5: if φ (cx – az, cy – bz) = 0 then show that ap + bq = c
Where p = 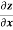 q =
q = 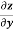
Solution: We have,
Φ(cx – az , cy – bz) = 0
φ(r , s) = 0
Where,

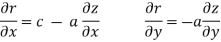

We know that,
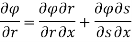
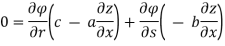
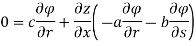
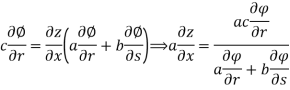
Again, we do
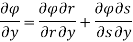
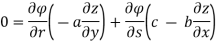

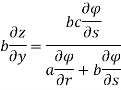
By adding the two results, we get
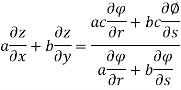

Example-6: If z is the function of x and y , and x =  , y =
, y = 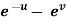 , then prove that,
, then prove that,
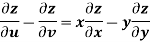
Solution: Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
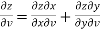 ………………..(2)
………………..(2)
Also there is,
x = 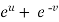 and y =
and y = 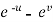 ,
,
Now,
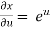 ,
, 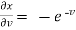 ,
, 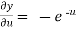 ,
, 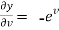
From equation(1) , we get
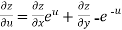 ……………….(3)
……………….(3)
And from eq. (2) , we get
 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
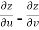 =
= 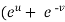 )
)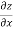 – (
– (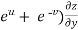
= x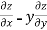
Hence proved.
Differentiability-
Let f(x) be a single valued function of the variable x,then,
f’(x) = 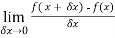
Provided that the limit exists and is dependent of the path along which 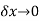
Example 7: suppose that the function,
f(z) = 4x + y + i( -x + 4y)
Discuss df/dz.
Solution: Here,
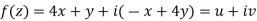
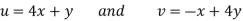
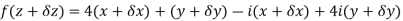
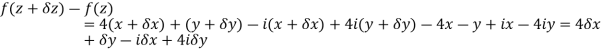
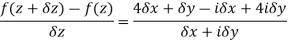
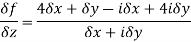
Example-2: if
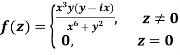 , Then df/dz , z = 0.
, Then df/dz , z = 0.
Solution:
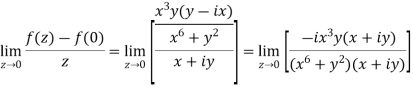

In calculus, the general Leibniz rule named after Gottfried Wilhelm Leibniz, generalizes the product rule (which is also known as "Leibniz's rule"). It states that if f and g are n-times differentiable functions, then the product fg is also n-times differentiable and its nth derivative is given by
(fg)n = 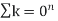 (nk) f(n-k).g(k)
(nk) f(n-k).g(k)
Alternatively, by letting F = f ∘ g (equiv., F(x) = f(g(x)) for all x), one can also write the chain rule in Lagrange's notation, as follows:
F’(X)= f’(g(x)).g’(x)
The chain rule may also be rewritten in Leibniz's notation in the following way. If a variable z depends on the variable y, which itself depends on the variable x (i.e., y and z are dependent variables), then z, via the intermediate variable of y, depends on x as well. In which case, the chain rule states that:

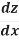 =
= 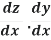
The Chain Rule Formula is as follows –
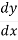 =
=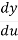 .
.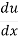
Example 1: Differentiate y = cos x2
Solution:
Given,
y = cos x2
Let u = x2, so that y = cos u
Therefore: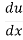 =2x
=2x
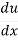 = -sin u
= -sin u
And so, the chain rule says:
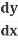 =
=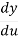 .
.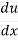
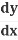 = -sin u × 2x
= -sin u × 2x
= -2x sin x2
Example 2:
Differentiate f(x)=(1+x2)5.
Solution:
Using the Chain rule,
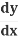 =
= 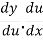
Let us take y = u5 and u = 1+x2
Then 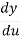 =
= 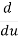 (u5) = 5u4
(u5) = 5u4
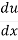 =
= 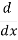 (1 + x2 )= 2x.
(1 + x2 )= 2x.
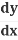 = 5u4⋅2x = 5(1+x2)4⋅2x
= 5u4⋅2x = 5(1+x2)4⋅2x
= 10x(1+x4)
Determine the image of a region under a given transformation of variables.
Compute the Jacobian of a given transformation.
Evaluate a double integral using a change of variables.
Evaluate a triple integral using a change of variables.
Example 1:
Evaluate  .dA
.dA
Solution:
Here’s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0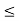 u
u 1
1
v=x-y , 0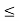 v
v 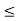 8
8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
4 Solving for x and y
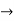
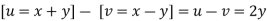
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
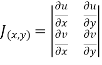 and
and 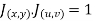

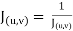

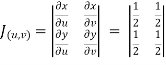
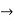
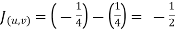
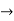
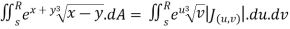
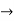
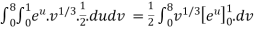

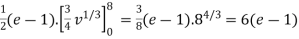


Example 2:
Evaluate 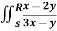 .dA
.dA
Solution:
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1 ;3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
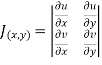 and
and 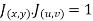

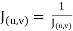
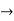
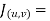
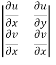
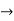 where
where 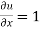 ,
, 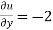 ,
, 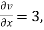
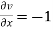
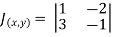 = -1+6 =5
= -1+6 =5
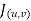 =
= 
Example 3:
Given a plane z= 3x+4y+2 that lies above the rectangle [0,5]  [1,4]. Find the surface area
[1,4]. Find the surface area
Solution:
The area of the surface with equation z=f(x,y),(x,y) D ,where
D ,where  are continuous,
are continuous,
Is A(S)= 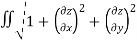 dA
dA
We have z=2+3x+4y.
Then, and
and 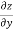 =4
=4
A(S) =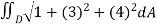
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) =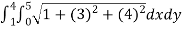
Evaluate the iterated integral.
A(S) =
=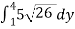
=15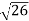
Example 4:
As an example, let us consider the following integral in two dimensions:
I=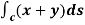
Solution: Where C is a straight line from the origin to (1,1), as shown the figure, Let s be the arc length measured from the origin. We then have
x =s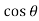 =
=
y=s sin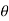 =
=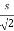
The endpoint (1,1) corresponds to s=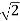 .Thus , the line integral becomes
.Thus , the line integral becomes
I=
Jacobians, Errors and Approximations, maxima and minima
Jacobians
If u and v be continuous and differentiable functions of two other independent variables x and y such as
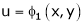 ,
,  then we define the determine
then we define the determine
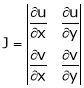 as Jacobian of u, v with respect to x, y
as Jacobian of u, v with respect to x, y
Similarly,
JJ’ = 1
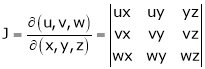
Actually, Jacobins are functional determines
Ex.
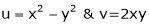 Calculate
Calculate 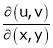
- If
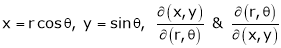
- If
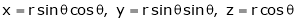
ST 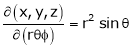
4.  find
find 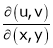
5. If  and
and 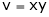 , find
, find 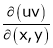
6. 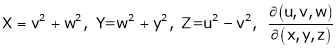
7. If 
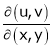
8. If 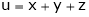 ,
,  ,
, 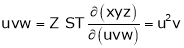
JJ1 = 1
If 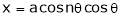 ,
, 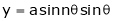
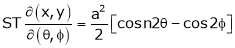
JJ1=1
Jacobian of composite function (chain rule)
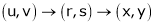
Then 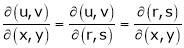
Ex.
- If
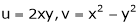
Where 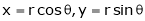
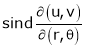
2. If 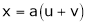
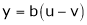 and
and 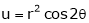
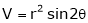
Find 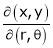
3. If 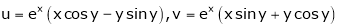
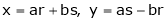
Find 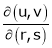
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
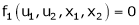 ,
, 
Then 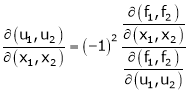
Similarly,
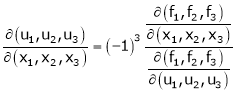
Ex.
If 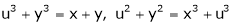
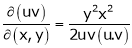
If 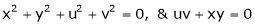
Find 
Partial derivative of implicit functions
Consider four variables u, v, x, y related by implicit function.
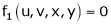 ,
, 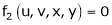
Then
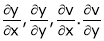
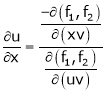
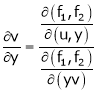
Ex.
If 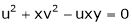 and
and 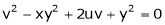
Find 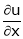
If 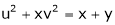 and
and 
Find 
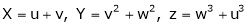
Find 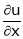
If 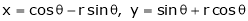
Find 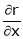
Example 1:
Determine the jacobian matrix of the function
f: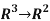 given by f(x,y,z)=(xy+2yz+2xy2z).
given by f(x,y,z)=(xy+2yz+2xy2z).
Solution:
We first write f = f(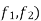 where
where 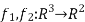 are given by the formulas
are given by the formulas  we know compute the gradients of these functions .we have that,
we know compute the gradients of these functions .we have that,
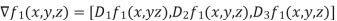
= [y,x+2z,2y]
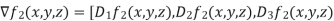
= [2y2z,4xyz,2xy2]
The jacobian matrix f is therefore the 2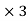 matrix whose first row is
matrix whose first row is 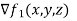 and the second row is
and the second row is 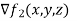 so
so
Df ( x ,y ,z) = 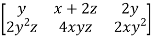
Example 2:
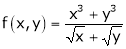
Solution: Consider 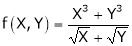
Put 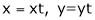
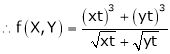
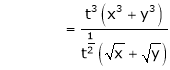
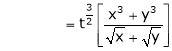
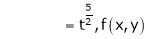 .
.
Thus degree of f(x, y) is 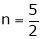
Note that
If  be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as

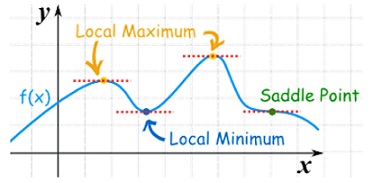
As we know that the value of a function at maximum point is called maximum value of a function. Similarly, the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variable
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 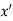 if and only if
if and only if 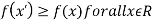
Minima is a minimum point  if and only if
if and only if 


Maxima and Minima of a function of two independent variables
Let  be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 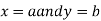 is said to be a maximum point of
is said to be a maximum point of  if
if
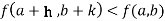
Or  =
= 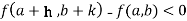
For all positive and negative values of h and k.
Similarly, the point 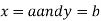 is said to be a minimum point of
is said to be a minimum point of 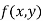 if
if
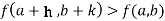
Or 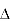 =
= 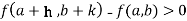
For all positive and negative values of h and k.
Saddle point: Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643287335_1028469.png)
At the point.
Stationary Value
The value 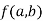 is said to be a stationary value of
is said to be a stationary value of 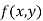 if
if
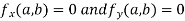
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 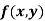
- Calculate
 .
. - Form and solve
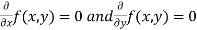 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 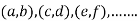
- Calculate the following values :
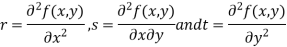
4. (a) If 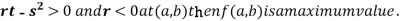
(b) If 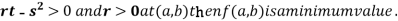
(c) If 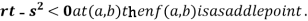
(d) If 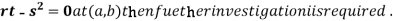
Example 1: Find out the maxima and minima of the function
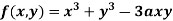
Solution: Given 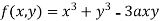 …(i)
…(i)
Partially differentiating (i) with respect to x we get
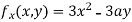 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
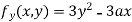 ….(iii)
….(iii)
Now, form the equations 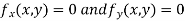
Using (ii) and (iii) we get
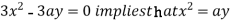
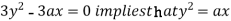
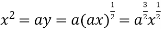 using above two equations
using above two equations
Squaring both side we get
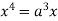
Or 
This show that 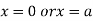
Also, we get 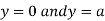
Thus, we get the pair of value as 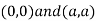
Now, we calculate
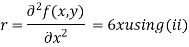
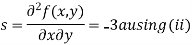
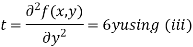
Putting above values in
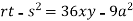
At point (0,0) we get
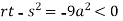
So, the point (0,0) is a saddle point.
At point 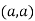 we get
we get
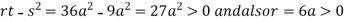
So, the point 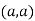 is the minimum point where
is the minimum point where 
In case 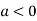
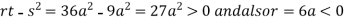
So, the point 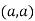 is the maximum point where
is the maximum point where 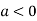
Example 2: Find the maximum and minimum point of the function
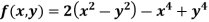
Partially differentiating given equation with respect to and x and y then equate them to zero
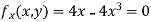
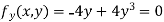
On solving above we get 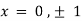
Also 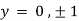
Thus, we get the pair of values (0,0), (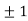 ,0) and (0,
,0) and (0,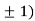
Now, we calculate
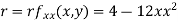
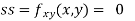
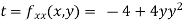
At the point (0,0)
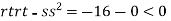
So function has saddle point at (0,0).
At the point (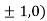
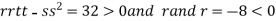
So the function has maxima at this point (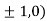 .
.
At the point (0,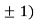
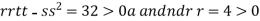
So the function has minima at this point (0,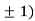 .
.
At the point (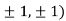
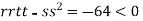
So the function has an saddle point at (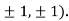
Example 3: Find the maximum and minimum value of 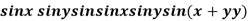
Let 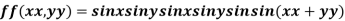
Solution: Partially differentiating given function with respect to x and y and equate it to zero
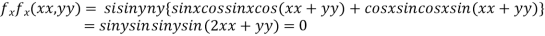 ..(i)
..(i)
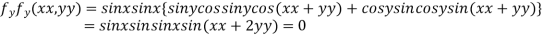 ..(ii)
..(ii)
On solving (i) and (ii) we get
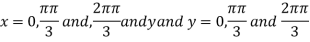
Thus, pair of values are 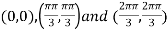
Now, we calculate
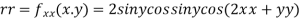
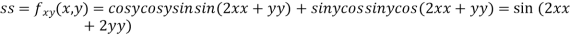
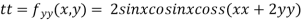
At the point (0,0)
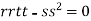
So further investigation is required
On the x axis y = 0, f(x,0) =0
On the line y=x, 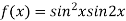
At the point 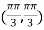
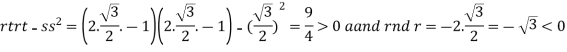
So that the given function has maximum value at 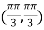
Therefore, maximum value of given function
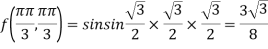
At the point 
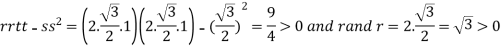
So that the given function has minimum value at 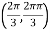
Therefore, minimum value of the given function

Let  be a function of x, y, z which to be discussed for stationary value.
be a function of x, y, z which to be discussed for stationary value.
Let 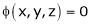 be a relation in x, y, z
be a relation in x, y, z
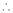 for stationary values we have,
for stationary values we have,
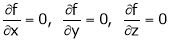
i.e. 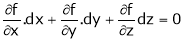 … (1)
… (1)
Also, from  we have
we have
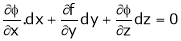 … (2)
… (2)
Let ‘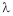 ’ be undetermined multiplier then multiplying equation (2) by
’ be undetermined multiplier then multiplying equation (2) by 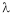 and adding in equation (1) we get,
and adding in equation (1) we get,
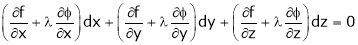
 … (3)
… (3)
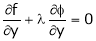 … (4)
… (4)
 … (5)
… (5)
Solving equation (3), (4) (5) & we get values of x, y, z and 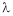 .
.
Example 1: Decampere a positive number ‘a’ in to three parts, so their product is maximum
Solution: Let x, y, z be the three parts of ‘a’ then we get.
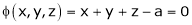 … (1)
… (1)
Here we have to maximize the product
i.e. 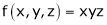
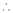 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,

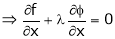 … (2)
… (2)
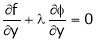 … (3)
… (3)
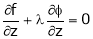 … (4)
… (4)
i.e.
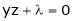 … (2)’
… (2)’
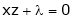 … (3)’
… (3)’
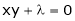 … (4)
… (4)

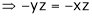
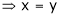
And 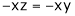
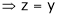

From (1)

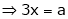
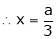
Thus 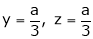 .
.
Hence their maximum product is 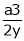 .
.
Example 2: Find the point on plane 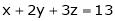 nearest to the point
nearest to the point
(1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let  be the point on sphere
be the point on sphere 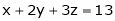 which is nearest to the point
which is nearest to the point 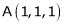 . Then shortest distance.
. Then shortest distance.


 Let
Let 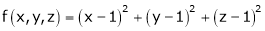
Under the condition 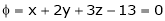 … (1)
… (1)
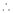 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
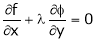
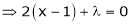 … (2)
… (2)
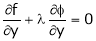
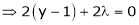 … (3)
… (3)
i.e.  &
&
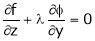
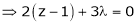 … (4)
… (4)
From (2) we get 
From (3) we get 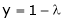
From (4) we get 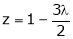
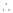 Equation (1) becomes
Equation (1) becomes
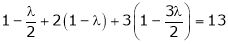
i.e. 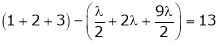
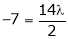
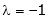
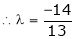
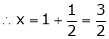
y = 2
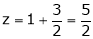
Textbooks:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 10/e, John Wiley & Sons, 2011.
2. B. S. Grewal, Higher Engineering Mathematics, 44/e, Khanna Publishers, 2017.
References:
1. R. K. Jain and S. R. K. Iyengar, Advanced Engineering Mathematics, 3/e, Alpha Science
International Ltd., 2002.
2. George B. Thomas, Maurice D. Weir and Joel Hass, Thomas Calculus, 13/e, Pearson
Publishers, 2013.
3. Glyn James, Advanced Modern Engineering Mathematics, 4/e, Pearson publishers, 201.