Unit 2
Mean value theorems
Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a , if

Differentiability- A function f(x) is said to be differentiable at x=a if
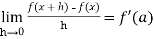 exists where ‘a’ belongs to I
exists where ‘a’ belongs to I
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
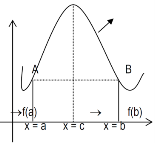
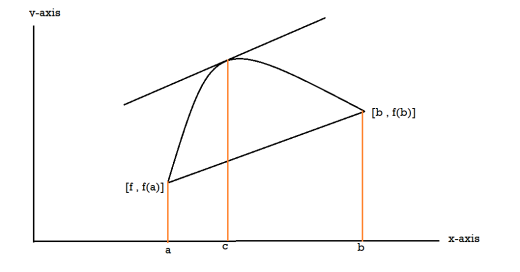
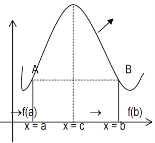
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
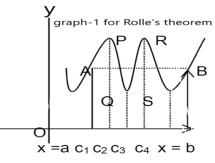
Slope of the tangent at P or Q,R, S, will be 0,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example 1: Verify Rolle’s theorem for the function f(x) = x(x+3)  in interval [-3, 0].
in interval [-3, 0].
Solution: First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x) 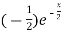 + (2x + 3)
+ (2x + 3)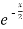
= 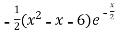
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Example 2: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Solution. (1) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+ 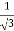 and 2 -
and 2 - 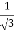
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Example 3: Verify the Rolle’s theorem for sin x in the interval [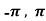 ]
]
Solution: Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now, f’(x) = cos x exists for all x in ( ) and
) and
f(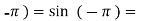 0
0
f(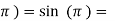 0
0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives, cos x = 0
x = 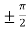
Here we notice that both intervals lie in (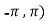 .
.
There exists, c = 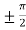
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a , b]
2. If it is differentiable in (a , b)
Then there atleast exists a value cϵ (a , b)
f’(c) = 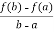
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that, g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab ,
Which gives,
A = 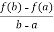 …………………..(2)
…………………..(2)
As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,, f’(c) = A,
From equation (2) , we get
f’(c) = 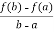 hence proved.
hence proved.
Example 1: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Solution: As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) =  =
= 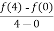 =
= 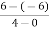 = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 
Here we see that the value of c lies between 0 and 4
Therefore, the given function is verified.
Example 2: Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].
Solution: We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) = 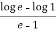 , let x = c,
, let x = c,
Then ,
f’(c) = 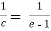
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem.
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a,b]
2. Both functions are differentiable in (a,b)
3. g’(x) ≠ 0 for any x ϵ (a,b)
These three exists atleast , x = c ϵ (a,b) , at which
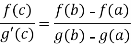
Proof: suppose, we define a functions,
h(x) = f(x) – A.g(x) …………………….(1)
So that h(a) = h(b) and A is a constant to be determined.
Now,
h(a) = f(a) – Ag(a)
h(b) = f(b) – A.g(b)
So that,
f(a) – Ag(a) = f(b) – A.g(b) , which gives
A = 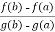 …………………………….(2)
…………………………….(2)
Now, h(x) is continuous in [a,b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a,b) as RHS of eq. (1) is diff. In (a,b)
Also,
h(a) = h(b)
Therefore, all the conditions of Rolle’s theorem are satisfied then there exists a Value x = cϵ (a, b)
So that h’(c) = 0
Differentiate eq.(1) w.r.t.x, we get
h’(x) = f’(x) – A.g’(x)
At x = c
h’(c) = f’(c) – A.g’(c)
0 = f’(c) – A.g’(c)
A = 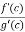
So that , we get
 where a<c<b
where a<c<b
Hence the Cauchy’s mean value theorem is proved.
Example 1: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cosx in [ 0, π/2]
Solution: It is given the,
f(x) = sin x and g(x) = cos x
Now,
f’(x) = cos x and g’(x) = - sin x
We know that both the functions are continuous in [ 0 , π/2] and differentiable in ( 0 , π/2 )
Also, g’(x) = -sin x ≠ 0 for all x ϵ( 0 , π/2 )
By Cauchy’s mean value theorem, we get
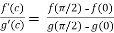 for some c: 0< c <
for some c: 0< c <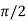
That means
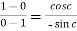 which gives,
which gives,
Cot c = 1
C = 
Now we see that  lies between 0 and
lies between 0 and 
Example 2: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]
Solution: We are given, f(x) = x⁴ and g(x) = x
Derivative of these functions,
f’(x) = 4x³ and g’(x) = 2x
Put these values in Cauchy’s formula, we get
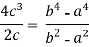
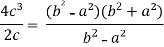
2c² = 
c² = 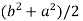
c = 
Now put the values of a = 1 and b = 2 ,we get
c = 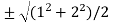 =
=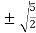 =
= 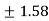 (approx)
(approx)
Hence the Cauchy’s theorem is verified.
Taylor’s Theorem-
If f(x + h) is a function of h which can be expanded in the ascending powers of h and is differentiable by any number of times with respect to h, then-
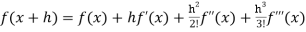 + …….+
+ …….+ 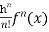 + ……..
+ ……..
Which is called Taylor’s theorem.
If we put x = a, we get-
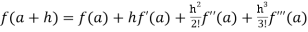 + …….+
+ …….+ 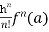 + …….. (1)
+ …….. (1)
Maclaurin’s Theorem-
If we put a = 0 and h = x then equation(1) becomes-
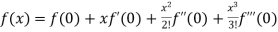 + …….
+ …….
Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
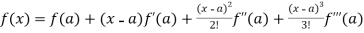 + …….
+ …….
Example 1: Express the polynomial 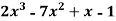 in powers of (x-2).
in powers of (x-2).
Solution: Here we have,
f(x) = 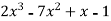
Differentiating the function w.r.t.x-
f’(x) = 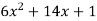
f’’(x) = 12x + 14
f’’’(x) = 12
f’’’’(x)=0
Now using Taylor’s theorem-
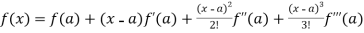 + ……. (1)
+ ……. (1)
Here we have, a = 2,
Put x = 2 in the derivatives of f(x), we get-
f(2) = 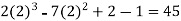
f’(2) = 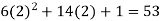
f’’(2) = 12(2)+14 = 38
f’’’(2) = 12 and f’’’’(2) = 0
Now put a = 2 and substitute the above values in equation (1), we get-
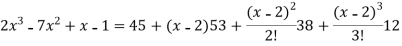
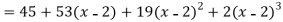
Example 2: Expand sin x in powers of 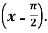
Solution: Let f(x) = sin x
Then,
= 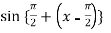
By using Taylor’s theorem-
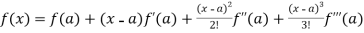 + ……. (1)
+ ……. (1)
Here f(x) = sin x and a = π/2
f’(x) = cosx, f’’(x) = - sin x, f’’’(x) = - cos x and so on.
Putting x = π/2, we get
f(x) = sin x = 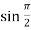 = 1
= 1
f’(x) = cos x = 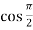 = 0
= 0
f’’(x) = -sin x = 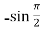 = -1
= -1
f’’’(x) = -cos x =  = 0
= 0
From equation (1) put a =  and substitute these values, we get-
and substitute these values, we get-
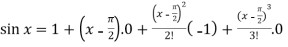 + …….
+ …….
= 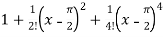 ………………………..
………………………..
Textbooks:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 10/e, John Wiley & Sons, 2011.
2. B. S. Grewal, Higher Engineering Mathematics, 44/e, Khanna Publishers, 2017.
References:
1. R. K. Jain and S. R. K. Iyengar, Advanced Engineering Mathematics, 3/e, Alpha Science
International Ltd., 2002.
2. George B. Thomas, Maurice D. Weir and Joel Hass, Thomas Calculus, 13/e, Pearson
Publishers, 2013.
3. Glyn James, Advanced Modern Engineering Mathematics, 4/e, Pearson publishers, 201.
Unit 2
Mean value theorems
Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a , if
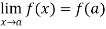
Differentiability- A function f(x) is said to be differentiable at x=a if
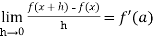 exists where ‘a’ belongs to I
exists where ‘a’ belongs to I
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
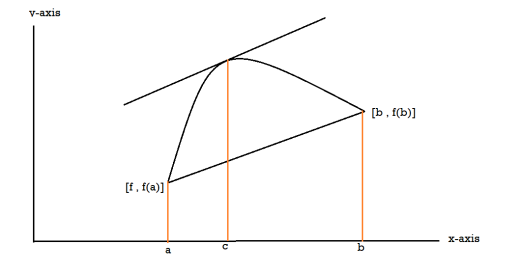
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
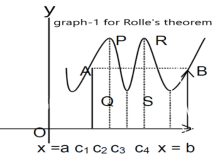
Slope of the tangent at P or Q,R, S, will be 0,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example 1: Verify Rolle’s theorem for the function f(x) = x(x+3) 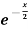 in interval [-3, 0].
in interval [-3, 0].
Solution: First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x)  + (2x + 3)
+ (2x + 3)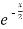
= 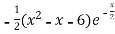
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
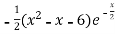 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Example 2: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Solution. (1) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+ 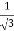 and 2 -
and 2 - 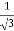
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Example 3: Verify the Rolle’s theorem for sin x in the interval [ ]
]
Solution: Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now, f’(x) = cos x exists for all x in (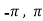 ) and
) and
f( 0
0
f(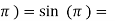 0
0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives, cos x = 0
x = 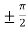
Here we notice that both intervals lie in (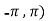 .
.
There exists, c = 
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a , b]
2. If it is differentiable in (a , b)
Then there atleast exists a value cϵ (a , b)
f’(c) = 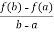
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that, g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab ,
Which gives,
A = 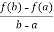 …………………..(2)
…………………..(2)
As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,, f’(c) = A,
From equation (2) , we get
f’(c) = 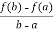 hence proved.
hence proved.
Example 1: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Solution: As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) = 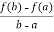 =
= 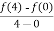 =
= 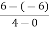 = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 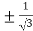
Here we see that the value of c lies between 0 and 4
Therefore, the given function is verified.
Example 2: Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].
Solution: We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) = 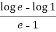 , let x = c,
, let x = c,
Then ,
f’(c) = 
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem.
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a,b]
2. Both functions are differentiable in (a,b)
3. g’(x) ≠ 0 for any x ϵ (a,b)
These three exists atleast , x = c ϵ (a,b) , at which
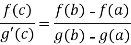
Proof: suppose, we define a functions,
h(x) = f(x) – A.g(x) …………………….(1)
So that h(a) = h(b) and A is a constant to be determined.
Now,
h(a) = f(a) – Ag(a)
h(b) = f(b) – A.g(b)
So that,
f(a) – Ag(a) = f(b) – A.g(b) , which gives
A = 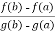 …………………………….(2)
…………………………….(2)
Now, h(x) is continuous in [a,b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a,b) as RHS of eq. (1) is diff. In (a,b)
Also,
h(a) = h(b)
Therefore, all the conditions of Rolle’s theorem are satisfied then there exists a Value x = cϵ (a, b)
So that h’(c) = 0
Differentiate eq.(1) w.r.t.x, we get
h’(x) = f’(x) – A.g’(x)
At x = c
h’(c) = f’(c) – A.g’(c)
0 = f’(c) – A.g’(c)
A = 
So that , we get
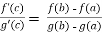 where a<c<b
where a<c<b
Hence the Cauchy’s mean value theorem is proved.
Example 1: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cosx in [ 0, π/2]
Solution: It is given the,
f(x) = sin x and g(x) = cos x
Now,
f’(x) = cos x and g’(x) = - sin x
We know that both the functions are continuous in [ 0 , π/2] and differentiable in ( 0 , π/2 )
Also, g’(x) = -sin x ≠ 0 for all x ϵ( 0 , π/2 )
By Cauchy’s mean value theorem, we get
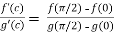 for some c: 0< c <
for some c: 0< c <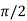
That means
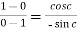 which gives,
which gives,
Cot c = 1
C = 
Now we see that  lies between 0 and
lies between 0 and 
Example 2: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]
Solution: We are given, f(x) = x⁴ and g(x) = x
Derivative of these functions,
f’(x) = 4x³ and g’(x) = 2x
Put these values in Cauchy’s formula, we get
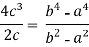
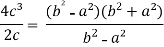
2c² = 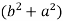
c² = 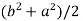
c = 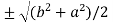
Now put the values of a = 1 and b = 2 ,we get
c =  =
=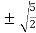 =
=  (approx)
(approx)
Hence the Cauchy’s theorem is verified.
Taylor’s Theorem-
If f(x + h) is a function of h which can be expanded in the ascending powers of h and is differentiable by any number of times with respect to h, then-
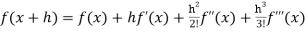 + …….+
+ …….+ 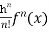 + ……..
+ ……..
Which is called Taylor’s theorem.
If we put x = a, we get-
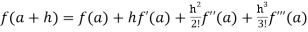 + …….+
+ …….+ 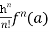 + …….. (1)
+ …….. (1)
Maclaurin’s Theorem-
If we put a = 0 and h = x then equation(1) becomes-
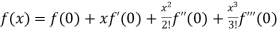 + …….
+ …….
Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
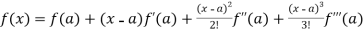 + …….
+ …….
Example 1: Express the polynomial 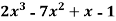 in powers of (x-2).
in powers of (x-2).
Solution: Here we have,
f(x) = 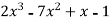
Differentiating the function w.r.t.x-
f’(x) = 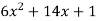
f’’(x) = 12x + 14
f’’’(x) = 12
f’’’’(x)=0
Now using Taylor’s theorem-
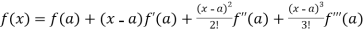 + ……. (1)
+ ……. (1)
Here we have, a = 2,
Put x = 2 in the derivatives of f(x), we get-
f(2) = 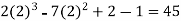
f’(2) = 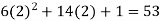
f’’(2) = 12(2)+14 = 38
f’’’(2) = 12 and f’’’’(2) = 0
Now put a = 2 and substitute the above values in equation (1), we get-
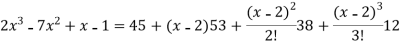
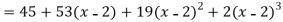
Example 2: Expand sin x in powers of 
Solution: Let f(x) = sin x
Then,
= 
By using Taylor’s theorem-
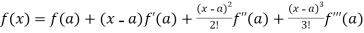 + ……. (1)
+ ……. (1)
Here f(x) = sin x and a = π/2
f’(x) = cosx, f’’(x) = - sin x, f’’’(x) = - cos x and so on.
Putting x = π/2, we get
f(x) = sin x = 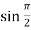 = 1
= 1
f’(x) = cos x = 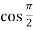 = 0
= 0
f’’(x) = -sin x = 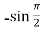 = -1
= -1
f’’’(x) = -cos x = 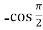 = 0
= 0
From equation (1) put a =  and substitute these values, we get-
and substitute these values, we get-
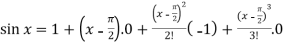 + …….
+ …….
= 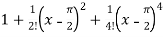 ………………………..
………………………..
Textbooks:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 10/e, John Wiley & Sons, 2011.
2. B. S. Grewal, Higher Engineering Mathematics, 44/e, Khanna Publishers, 2017.
References:
1. R. K. Jain and S. R. K. Iyengar, Advanced Engineering Mathematics, 3/e, Alpha Science
International Ltd., 2002.
2. George B. Thomas, Maurice D. Weir and Joel Hass, Thomas Calculus, 13/e, Pearson
Publishers, 2013.
3. Glyn James, Advanced Modern Engineering Mathematics, 4/e, Pearson publishers, 201.